3.6: Детермінанти та правило Крамера

Цілі навчання

• Обчислити детермінант\(2\times 2\) матриці.
• Використовуйте правило Крамера для вирішення систем лінійних рівнянь з двома змінними.
• Обчислити детермінант\(3\times 3\) матриці.
• Використовуйте правило Крамера для вирішення систем лінійних рівнянь з трьома змінними.

Лінійні системи двох змінних та правило Крамера

Нагадаємо, що матриця - це прямокутний масив чисел, що складається з рядків і стовпців. Класифікуємо матриці за кількістю рядків\(n\) і кількістю стовпців\(m\). Наприклад,\(3\times 4\) матриця, читається «матриця 3 на 4», - це та, яка складається з\(3\) рядків і\(4\) стовпців. Квадратна матриця ²⁹ - це матриця, де кількість рядків збігається з кількістю стовпців. У цьому розділі ми окреслимо інший метод розв'язання лінійних систем з використанням спеціальних властивостей квадратних матриць. Почнемо з розгляду наступної матриці\(2\times 2\) коефіцієнтів\(A\),

\(A = \left[ \begin{array} { c c} { a _ { 1 }} &{ b _ { 1 } } \\ { a _ { 2 }} &{ b _ { 2 } } \end{array} \right]\)

Визначник ³⁰\(2\times 2\) матриці, що позначається вертикальними лініями\(|A|\), або більш компактно як det (A), визначається наступним чином:

Малюнок\(\PageIndex{1}\)

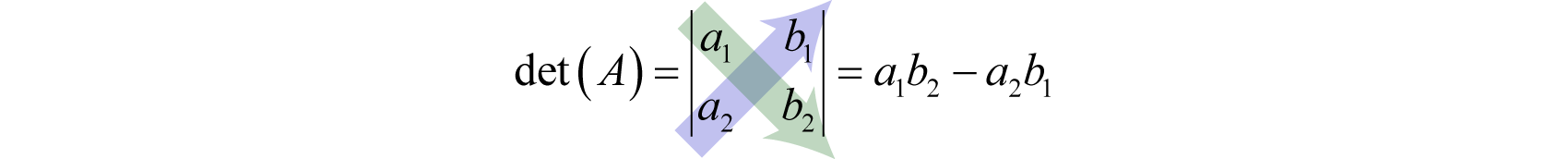
Детермінант - це дійсне число, яке отримують шляхом віднімання добутків значень по діагоналі.

Приклад\(\PageIndex{1}\):

Розрахувати:\(\left| \begin{array} { l } { 3 - 5 } \\ { 2 - 2 } \end{array} \right|\)

Рішення

Вертикальна лінія по обидва боки матриці вказує на те, що нам потрібно обчислити детермінант.

\(\begin{aligned} \left| \begin{array} { c c } { 3} &{ - 5 } \\ { 2} &{ - 2 } \end{array} \right| & = 3 ( - 2 ) - 2 ( - 5 ) \\ & = - 6 + 10 \\ & = 4 \end{aligned}\)

Відповідь:

\(4\)

Приклад\(\PageIndex{2}\):

Розрахувати:\(\left| \begin{array} { c c } { - 6} &{4 } \\ { 0 } & {3}\end{array} \right]\)

Рішення

Зверніть увагу, що матриця дана у верхній трикутній формі.

\(\begin{aligned} \left| \begin{array} { c c } { - 6} &{4 } \\ { 0} &{3 } \end{array} \right| & = - 6 ( 3 ) - 4 ( 0 ) \\ & = - 18 - 0 \\ & = - 18 \end{aligned}\)

Відповідь:

\(-18\)

Ми можемо розв'язувати лінійні системи з двома змінними, використовуючи детермінанти. Починаємо з загальної\(2\times 2\) лінійної системи і вирішуємо для\(y\). Щоб усунути змінну\(x\), помножте перше рівняння на,\(−a_{2}\) а друге рівняння на\(a_{1}\).

\(\left\{ \begin{array} { l l } { a _ { 1 } x + b _ { 1 } y = c _ { 1 } } & { \stackrel { \times \left( - a _ { 2 } \right) } { \Longrightarrow } } \\ { a _ { 2 } x + b _ { 2 } y = c _ { 2 } } & { \underset { \times a _ { 1 } } { \Longrightarrow }} \end{array} \right. \left\{ \begin{array} { c } { - a _ { 1 } a _ { 2 } x - a _ { 2 } b _ { 1 } y = - a _ { 2 } c _ { 1 } } \\ { a _ { 1 } a _ { 2 } x + a _ { 1 } b _ { 2 } y = a _ { 1 } c _ { 2 } } \end{array} \right.\)

Це призводить до еквівалентної лінійної системи, де змінна\(x\) вишикується для усунення. Тепер додаємо рівняння, які ми маємо

Малюнок\(\PageIndex{2}\)

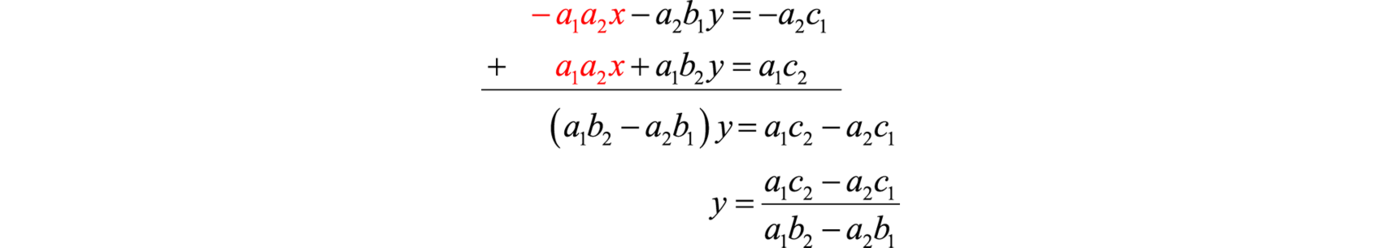
І чисельник, і знаменник дуже схожі на визначник\(2\times 2\) матриці. По суті, це так. Знаменник - визначник матриці коефіцієнтів. А чисельник - це визначник матриці, утвореної заміною стовпця, що представляє коефіцієнти\(y\) з відповідним стовпцем констант. Позначається ця спеціальна матриця\(D_{y}\).

\(y = \frac{D_{y}}{D} =\frac{\left| \begin{array} { c c } { a _ { 1 }} &{\color{Cerulean}{ c _ { 1} } } \\ {\color{black}{ a _ { 2 }}} &{ \color{Cerulean}{c _ { 2} } } \end{array} \right|}{\left| \begin{array} { c c } { a _ { 1 }} &{ b _ { 1 } } \\ { a _ { 2 }}&{ b _ { 2 } } \end{array} \right|}= \frac { a _ { 1 } c _ { 2 } - a _ { 2 } c _ { 1 } } { a _ { 1 } b _ { 2 } - a _ { 2 } b _ { 1 } } \)

Значення для\(x\) можна вивести аналогічним чином.

\(x = \frac{D_{x}}{D} =\frac{\left| \begin{array} { c c } { \color{Cerulean}{c _ { 1} }} &{ \color{black}{b _ { 1}} } \\ {\color{Cerulean}{ c _ { 2 }}} &{ \color{black}{b _ { 2} } } \end{array} \right|}{\left| \begin{array} { c c } { a _ { 1 }} &{ b _ { 1 } } \\ { a _ { 2 }}&{ b _ { 2 } } \end{array} \right|}= \frac { c _ { 1 } b _ { 2 } - c _ { 2 } b _ { 1 } } { a _ { 1 } b _ { 2 } - a _ { 2 } b _ { 1 } } \)

Загалом, ми можемо сформувати доповнену матрицю наступним чином:

\(\left\{ \begin{array} { l l } { a _ { 1 } x + b _ { 1 } y = c _ { 1 } } \\ { a _ { 2 } x + b _ { 2 } y = c _ { 2 } } \end{array} \right. \Leftrightarrow \left[ \begin{array} { c c | c } { a _ { 1 }} &{ b _ { 1 }} &{\color{Cerulean}{c _ { 1}} } \\ { a _ { 2 }} &{ b _ { 2 }} &{ \color{Cerulean}{c _ { 2} } } \end{array} \right]\)

а потім визначити\(D, D_{x}\) і\(D_{y}\) шляхом обчислення наступних детермінанти.

\(D = \left| \begin{array} { c c } { a _ { 1 }}&{ b _ { 1 } } \\ { a _ { 2 }}&{ b _ { 2 } } \end{array} \right| \quad D _ { x } = \left| \begin{array} { c c} { \color{Cerulean}{c _ { 1 }}}&{ \color{black}{b _ { 1} } } \\ { \color{Cerulean}{c _ { 2} }}&{ \color{black}{b _ { 2} } } \end{array} \right| \quad D _ { y } = \left| \begin{array} { c c} { a _ { 1 }}&{\color{Cerulean}{ c _ { 1} } } \\ { a _ { 2 }}&{\color{Cerulean}{ c _ { 2} } } \end{array} \right|\)

Розв'язок системи з точки зору детермінант, описаних вище, коли D ≠ 0, називається правилом Крамера ³¹.

\(\begin{array} { c } { \color{Cerulean} { Cramer's\: Rule } } \\ { ( x , y ) = \left( \frac { D _ { x } } { D } , \frac { D _ { y } } { D } \right) } \end{array}\)

Ця теорема названа на честь Габріеля Крамера (1704 - 1752).

Малюнок\(\PageIndex{3}\): Габріель Крамер

Етапи розв'язання лінійної системи з двома змінними за допомогою детермінант (правило Крамера) викладені в наступному прикладі.

Приклад\(\PageIndex{3}\):

Вирішіть за допомогою правила Крамера:\(\left\{ \begin{array} { c } { 2 x + y = 7 } \\ { 3 x - 2 y = - 7 } \end{array} \right.\).

Рішення

Переконайтеся, що лінійна система знаходиться в стандартній формі перед початком цього процесу.

Крок 1: Побудуйте розширену матрицю та сформуйте матриці, що використовуються в правилі Крамера.

\(\left\{ \begin{array} { c c } { 2 x + y = 7 } \\ { 3 x - 2 y = - 7 } \end{array} \right. \Rightarrow \left[ \begin{array} { c c |c } { 2 } & { 1 } & { \color{Cerulean}{7} } \\ { 3 } & { - 2 } & { \color{Cerulean}{- 7} } \end{array} \right]\)

У квадратній матриці, яка використовується для визначення\(D_{x}\), замініть перший стовпець матриці коефіцієнтів на константи. У квадратній матриці, яка використовується для визначення\(D_{y}\), замініть другий стовпець на константи.

\(D = \left| \begin{array} { c c } { 2 } & { 1 } \\ { 3 } & { - 2 } \end{array} \right| \quad D _ { x } = \left| \begin{array} { c c} { \color{Cerulean}{7} } & { \color{black}{1} } \\ { \color{Cerulean}{- 7} } & { \color{black}{- 2} } \end{array} \right| \quad D _ { y } = \left| \begin{array} { c c } { 2 } & {\color{Cerulean}{ 7} } \\ { 3 } & { \color{Cerulean}{- 7} } \end{array} \right|\)

Крок 2: Обчисліть детермінанти.

\(D _ { x } = \left| \begin{array} { r r } { 7 } & { 1 } \\ { - 7 } & { - 2 } \end{array} \right| = 7 ( - 2 ) - ( - 7 ) ( 1 ) = - 14 + 7 = - 7\)

\(D _ { y } = \left| \begin{array} { r r } { 2 } & { 7 } \\ { 3 } & { - 7 } \end{array} \right| = 2 ( - 7 ) - 3 ( 7 ) = - 14 - 21 = - 35\)

\(D = \left| \begin{array} { r r } { 2 } & { 1 } \\ { 3 } & { - 2 } \end{array} \right| = 2 ( - 2 ) - 3 ( 1 ) = - 4 - 3 = - 7\)

Крок 3: Використовуйте правило Крамера для обчислення\(x\) і\(y\).

\(x = \frac { D _ { x } } { D } = \frac { - 7 } { - 7 } = 1 \quad \text { and } \quad y = \frac { D _ { y } } { D } = \frac { - 35 } { - 7 } = 5\)

Тому одночасне рішення\((x, y) = (1,5)\).

Крок 4: Перевірка необов'язкова; однак, ми робимо це тут заради повноти.

Таблиця\(\PageIndex{1}\)

\(\color{Cerulean}{Check\:\:}\color{YellowOrange}{(1,5)}\)
Рівняння 1	Рівняння 2
\(\begin{array} { r } { 2 x + y = 7 } \\ { 2 ( \color{Cerulean}{1}\color{black}{ )} + ( \color{Cerulean}{5} \color{black}{)} = 7 } \\ { 2 + 5 = 7 } \\ { 7 = 7 } \color{Cerulean}{✓} \end{array}\)	\(\begin{array} { r } { 3 x - 2 y = - 7 } \\ { 3 ( \color{Cerulean}{1}\color{black}{ )} - 2 ( \color{Cerulean}{5}\color{black}{ )} = - 7 } \\ { 3 - 10 = - 7 } \\ { - 7 = - 7 } \color{Cerulean}{✓} \end{array}\)

Відповідь:

\((1,5)\)

Приклад\(\PageIndex{4}\):

Вирішіть за допомогою правила Крамера:\(\left\{ \begin{array} { c } { 3 x - y = - 2 } \\ { 6 x + 4 y = 2 } \end{array} \right.\).

Рішення

Далі слідує відповідна розширена матриця коефіцієнтів.

\(\left\{ \begin{array} { c } { 3 x - y = - 2 } \\ { 6 x + 4 y = 2 } \end{array} \right. \Rightarrow \left[ \begin{array} { c c |c } { 3 } & { - 1 } & { \color{Cerulean}{- 2} } \\ { 6 } & { 4 } & { \color{Cerulean}{2} } \end{array} \right]\)

І ми маємо,

\(D _ { x } = \left| \begin{array} { r r } { \color{Cerulean}{- 2} } & { \color{black}{- 1} } \\ { \color{Cerulean}{2} } & {\color{black}{ 4} } \end{array} \right| = - 8 - ( - 2 ) = - 8 + 2 = - 6\)

\(D _ { y } = \left| \begin{array} { r r } { 3 } & { \color{Cerulean}{- 2} } \\ { 6 } & { \color{Cerulean}{2} } \end{array} \right| = 6 - ( - 12 ) = 6 + 12 = 18\)

\(D = \left| \begin{array} { r r } { 3 } & { - 1 } \\ { 6 } & { 4 } \end{array} \right| = 12 - ( - 6 ) = 12 + 6 = 18\)

Скористайтеся правилом Крамера, щоб знайти рішення.

\(x = \frac { D _ { x } } { D } = \frac { - 6 } { 18 } = - \frac { 1 } { 3 } \quad \text { and } \quad y = \frac { D _ { y } } { D } = \frac { 18 } { 18 } = 1\)

Відповідь:

\((-\frac{1}{3}, 1)\)

Вправа\(\PageIndex{1}\)

Вирішіть за допомогою правила Крамера:\(\left\{ \begin{array} { c } { 5 x - 3 y = - 7 } \\ { - 7 x + 6 y = 11 } \end{array} \right.\).

Відповідь

\((-1, \frac{2}{3})\)

www.youtube.com/В/TR3J8OQZZY

Коли детермінант матриці\(D\) коефіцієнтів дорівнює нулю, формули правила Крамера невизначені. При цьому система або залежна, або суперечлива в залежності від значень\(D_{x}\) і\(D_{y}\). Коли\(D = 0\) і те,\(D_{x} = 0\) і\(D_{y} = 0\) інше, і система залежить. Коли\(D = 0\) і або\(D_{x}\) або\(D_{y}\) є ненульовим, то система суперечлива.

\(\begin{array} { l } { \text { When } D = 0 } \\ { D _ { x } = 0 \text { and } D _ { y } = 0 \Rightarrow } \:\:\color{Cerulean}{Dependent\:System} \\ { D _ { x } \neq 0 \text { or } D _ { y } \neq 0 \:\:\:\Rightarrow } \:\:\color{Cerulean}{Inconsistent\:System}\end{array}\)

Приклад\(\PageIndex{5}\):

Вирішіть за допомогою правила Крамера:\(\left\{ \begin{array} { l } { x + \frac { 1 } { 5 } y = 3 } \\ { 5 x + y = 15 } \end{array} \right.\).

Рішення

Далі йде відповідна доповнена матриця.

\(\left\{ \begin{array} { l } { x + \frac { 1 } { 5 } y = 3 } \\ { 5 x + y = 15 } \end{array} \right. \Rightarrow \left[ \begin{array} { c c |c } { 1} &{ \frac { 1 } { 5 }}&{ \color{Cerulean}{3} } \\ { 5}&{1} &{ \color{Cerulean}{15} } \end{array} \right]\)

А ми маємо наступне.

\(D _ { x } = \left| \begin{array} { c c } {\color{Cerulean}{ 3}} &{\color{black}{ \frac { 1 } { 5} } } \\ { \color{Cerulean}{15} } & {\color{black}{ 1} } \end{array} \right| = 3 - 3 = 0\)

\(D _ { y } = \left| \begin{array} { l } { 1 } & { \color{Cerulean}{3} } \\ { 5 } & {\color{Cerulean}{ 15} } \end{array} \right| = 15 - 15 = 0\)

\(D = \left| \begin{array} { c c } { 1 } & { \frac { 1 } { 5 } } \\ { 5 } & { 1 } \end{array} \right| = 1 - 1 = 0\)

Якщо ми спробуємо використовувати правило Крамера, яке ми маємо,

\(x = \frac { D _ { x } } { D } = \frac { 0 } { 0 } \quad \text { and } \quad y = \frac { D _ { y } } { D } = \frac { 0 } { 0 }\)

обидва з яких є невизначені величини. Тому що\(D = 0\) і те,\(D_{x} = 0\) і інше, і\(D_{y} = 0\) ми знаємо, що це залежна система. Насправді, ми можемо бачити, що обидва рівняння представляють одну і ту ж лінію, якщо ми вирішуємо для\(y\).

\(\left\{ \begin{array} { l } { x + \frac { 1 } { 5 } y = 3 } \\ { 5 x + y = 15 } \end{array} \right. \Rightarrow \left\{ \begin{array} { l } { y = - 5 x + 15 } \\ { y = - 5 x + 15 } \end{array} \right.\)

Тому ми можемо представити всі рішення\((x, −5x + 15)\), де\(x\) є дійсним числом.

Відповідь:

\(( x , - 5 x + 15 )\)

Вправа\(\PageIndex{2}\)

Вирішіть за допомогою правила Крамера:\(\left\{ \begin{array} { l } { 3 x - 2 y = 10 } \\ { 6 x - 4 y = 12 } \end{array} \right.\).

Відповідь

\(\varnothing\)

www.youtube.com/В/Д2ЛДКЮ 321НК

Лінійні системи трьох змінних та правило Крамера

Розглянемо наступну матрицю\(3\times 3\) коефіцієнтів\(A\),

\(A = \left[ \begin{array} { c c c } { a _ { 1 }} &{ b _ { 1 }}&{ c _ { 1 } } \\ { a _ { 2 }}&{ b _ { 2 }}&{ c _ { 2 } } \\ { a _ { 3 }}&{ b _ { 3 }}&{ c _ { 3 } } \end{array} \right]\)

Визначник цієї матриці визначається наступним чином:

\(\operatorname { det } ( A ) = \left| \begin{array} { l l l } { a _ { 1 } } & { b _ { 1 } } & { c _ { 1 } } \\ { a _ { 2 } } & { b _ { 2 } } & { c _ { 2 } } \\ { a _ { 3 } } & { b _ { 3 } } & { c _ { 3 } } \end{array} \right| \\ = a _ { 1 } \left| \begin{array} { c c } { b _ { 2 } } & { c _ { 2 } } \\ { b _ { 3 } } & { c _ { 3 } } \end{array} \right| - b _ { 1 } \left| \begin{array} { c c } { a _ { 2 } } & { c _ { 2 } } \\ { a _ { 3 } } & { c _ { 3 } } \end{array} \right| + c _ { 1 } \left| \begin{array} { l l } { a _ { 2 } } & { b _ { 2 } } \\ { a _ { 3 } } & { b _ { 3 } } \end{array} \right| \\= a _ { 1 } \left( b _ { 2 } c _ { 3 } - b _ { 3 } c _ { 2 } \right) - b _ { 1 } \left( a _ { 2 } c _ { 3 } - a _ { 3 } c _ { 2 } \right) + c _ { 1 } \left( a _ { 2 } b _ { 3 } - a _ { 3 } b _ { 2 } \right)\)

Тут кожен\(2\times 2\) детермінант називається мінор ³² від попереднього фактора. Зверніть увагу, що фактори є елементами в першому рядку матриці і що вони чергуються за знаком\((+ − +)\).

Приклад\(\PageIndex{6}\):

Розрахувати:\(\left| \begin{array} { r r r } { 1 } & { 3 } & { 2 } \\ { 2 } & { - 1 } & { 3 } \\ { 0 } & { 5 } & { - 1 } \end{array} \right|\)

Рішення

Щоб легко визначити мінор кожного фактора в першому рядку, ми вибудовуємо перший рядок і відповідний стовпець. Визначник матриці елементів, що залишилися, визначає відповідний мінор.

Малюнок\(\PageIndex{4}\)

Подбайте про чергування ознак факторів в першому ряду. Розширення неповнолітніми приблизно першого ряду слід:

\(\left| \begin{array} { r r r }\color{Cerulean}{ { 1 }} & \color{Cerulean}{ { 3 }} & \color{Cerulean}2 \\ {\color{black}{ 2} } & { - 1 } & { 3 } \\ { 0 } & { 5 } & { - 1 } \end{array} \right| = \color{Cerulean}{1}\color{black}{ \left| \begin{array} { r r } { - 1 } & { 3 } \\ { 5 } & { - 1 } \end{array} \right|} -\color{Cerulean}{ 3}\color{black}{ \left| \begin{array} { r r } { 2 } & { 3 } \\ { 0 } & { - 1 } \end{array} \right|} + \color{Cerulean}{2}\color{black}{ \left| \begin{array} { c c } { 2 } & { - 1 } \\ { 0 } & { 5 } \end{array} \right|} \\ \begin{array} { l } { = 1 ( 1 - 15 ) - 3 ( - 2 - 0 ) + 2 ( 10 - 0 ) } \\ { = 1 ( - 14 ) - 3 ( - 2 ) + 2 ( 10 ) } \\ { = - 14 + 6 + 20 } \\ { = 12 } \end{array}\)

Відповідь:

\(12\)

Розширення неповнолітніми може виконуватися щодо будь-якого рядка або будь-якого стовпця. Знак коефіцієнтів, що визначаються обраним рядком або стовпцем, буде чергуватися відповідно до наступного знакового масиву.

\(\left[ \begin{array} { c } { + - + } \\ { - + - } \\ { + - + } \end{array} \right]\)

Тому для розширення приблизно другого ряду будемо чергувати знаки, починаючи з протилежного першого елемента. Ми можемо розширити попередній приклад щодо другого рядка, щоб показати, що виходить однакова відповідь для визначника.

Малюнок\(\PageIndex{5}\)

І ми можемо написати,

\(\left| \begin{array} { c c c } { 1 } & { 3 } & { 2 } \\ { \color{Cerulean}{2} } & {\color{Cerulean}{ - 1} } & { \color{Cerulean}{3} } \\ { \color{black}{0} } & { 5 } & { - 1 } \end{array} \right| = - ( \color{Cerulean}{2}\color{black}{ )} \left| \begin{array} { c c } { 3 } & { 2 } \\ { 5 } & { - 1 } \end{array} \right| + ( \color{Cerulean}{- 1}\color{black}{ )} \left| \begin{array} { c c } { 1 } & { 2 } \\ { 0 } & { - 1 } \end{array} \right| - ( \color{Cerulean}{3}\color{black}{ )} \left| \begin{array} { c } { 13 } \\ { 05 } \end{array} \right|\\ \begin{array} { l } { = - 2 ( - 3 - 10 ) - 1 ( - 1 - 0 ) - 3 ( 5 - 0 ) } \\ { = - 2 ( - 13 ) - 1 ( - 1 ) - 3 ( 5 ) } \\ { = 26 + 1 - 15 } \\ { = 12 } \end{array}\)

Зверніть увагу, що отримуємо той же відповідь\(12\).

Приклад\(\PageIndex{7}\):

Розрахувати:\(\left| \begin{array} { c c c } { 4 } & { 3} &{0 } \\ { 6 } & { \frac { 1 } { 2 } } & { 2 } \\ { 4 } & { 1 } & { 0 } \end{array} \right|\)

Рішення

Обчислення спрощуються, якщо ми розгорнемо приблизно третій стовпець, оскільки він містить два нулі.

Малюнок\(\PageIndex{6}\)

Розширення неповнолітніми приблизно в третій графі слід:

\(\left| \begin{array} { c c c } { 4 } & { 3} &{\color{Cerulean}{0} } \\ { 6 } & { \frac { 1 } { 2 } } & { \color{Cerulean}{2} } \\ { 4 } & { 1} &{\color{Cerulean}{0} } \end{array} \right| = \color{Cerulean}{0}\color{black}{ \left| \begin{array} { c c } { 6} &{ \frac { 1 } { 2 } } \\ { 4 } & { 1 } \end{array} \right|} - \color{Cerulean}{2}\color{black}{ \left| \begin{array} { c c } { 4} &{3 } \\ { 4} &{1 } \end{array} \right|} + \color{Cerulean}{0}\color{black}{ \left| \begin{array} { c c } { 4} &{3 } \\ { 6} &{ \frac { 1 } { 2 } } \end{array} \right|} \\ \begin{array} { l } { = 0 - 2 ( 4 - 12 ) + 0 } \\ { = - 2 ( - 8 ) } \\ { = 16 } \end{array}\)

Відповідь:

\(16\)

Слід зазначити, що існують і інші методики, що використовуються для запам'ятовування того, як обчислити детермінант\(3\times 3\) матриці. Крім того, у багатьох сучасних калькуляторах і системах комп'ютерної алгебри можна знайти детермінант матриць. Вам пропонується дослідити цю багату тему.

Ми можемо розв'язувати лінійні системи з трьома змінними, використовуючи детермінанти. Для цього починаємо з доповненої матриці коефіцієнтів,

\(\left\{ \begin{array} { l } { a _ { 1 } x + b _ { 1 } y + c _ { 1 } z = d _ { 1 } } \\ { a _ { 2 } x + b _ { 2 } y + c _ { 2 } z = d _ { 2 } } \\ { a _ { 3 } x + b _ { 3 } y + c _ { 3 } z = d _ { 3 } } \end{array} \right. \Leftrightarrow \left[ \begin{array} { c c c | c } { a _ { 1 }} &{ b _ { 1 }} &{ c _ { 1 }} &{\color{Cerulean}{ d _ { 1} }} \\ { a _ { 2 }} &{ b _ { 2 }} &{ c _ { 2 }} & {\color{Cerulean}{d _ { 2} }} \\ { a _ { 3 }} &{ b _ { 3} }&{ c _ { 3} } &{\color{Cerulean}{d _ { 3}} } \end{array} \right]\)

\(D\)Дозволяти представляти детермінант матриці коефіцієнтів,

\(D = \left| \begin{array} { c c c } { a _ { 1 }} &{ b _ { 1 } } &{c _ { 1 } } \\ { a _ { 2 }} &{ b _ { 2} }&{ c _ { 2 } } \\ { a _ { 3 }}&{ b _ { 3} }&{ c _ { 3 } } \end{array} \right|\)

Потім визначають\(D_{x}, D_{y}\), і\(D_{z}\) обчисливши наступні детермінанти.

\(D _ { x } = \left| \begin{array} { c c c } { \color{Cerulean}{d _ { 1 }}} &{\color{black}{ b _ { 1} }} &{ c _ { 1 } } \\ { \color{Cerulean}{d _ { 2} }} &{\color{Cerulean}{ b _ { 2} }} &{ c _ { 2 } } \\ { \color{Cerulean}{d _ { 3} }}&{\color{black}{ b _ { 3} }}&{ c _ { 3 } } \end{array} \right| D _ { y } = \left| \begin{array} { c c c } { a _ { 1 }} &{ \color{Cerulean}{d _ { 1} }}&{ \color{black}{c _ { 1} } } \\ { a _ { 2 }} &{ \color{Cerulean}{d _ { 2} }} &{ \color{black}{c _ { 2} } } \\ { a _ { 3 }} &{ \color{Cerulean}{d _ { 3} }}&{ \color{black}{c _ { 3} } } \end{array} \right| D _ { z } = \left| \begin{array} { c c c } { a _ { 1 }}&{ b _ { 1 }}&{\color{Cerulean}{ d _ { 1} } } \\ { a _ { 2 }}&{ b _ { 2 }}&{\color{Cerulean}{ d _ { 2 }} } \\ { a _ { 3 }}&{ b _ { 3 } }&{\color{Cerulean}{d _ { 3} } } \end{array} \right|\)

Коли\(D ≠ 0\), рішення системи з точки зору визначників, описаних вище, можна розрахувати за правилом Крамера:

\(\begin{array} { c } { \color{Cerulean} { Cramer's\: Rule } } \\ { ( x , y , z ) = \left( \frac { D _ { x } } { D } , \frac { D _ { y } } { D } , \frac { D _ { z } } { D } \right) } \end{array}\)

Використовуйте це для ефективного вирішення систем з трьома змінними.

Приклад\(\PageIndex{1}\):

Вирішіть за допомогою правила Крамера:\(\left\{ \begin{array} { l } { 3 x + 7 y - 4 z = 0 } \\ { 2 x + 5 y - 3 z = 1 } \\ { - 5 x + 2 y + 4 z = 8 } \end{array} \right.\).

Рішення

Почніть з визначення відповідної доповненої матриці.

\(\left\{ \begin{array} { c c } { 3 x + 7 y - 4 z = 0 } \\ { 2 x + 5 y - 3 z = 1 } \\ { - 5 x + 2 y + 4 z = 8 } \end{array} \right. \Leftrightarrow \left[ \begin{array} { c c | c } { 37}&{ - 4}&{\color{Cerulean}{0} } \\ { 25}&{ - 3}&{\color{Cerulean}{1} } \\ { - 52}&{4}&{\color{Cerulean}{8} } \end{array} \right]\)

Далі обчислюємо детермінант матриці коефіцієнтів.

\(D = \left| \begin{array} { r r r } { \color{Cerulean}{3} } & { \color{Cerulean}{7} } & { \color{Cerulean}{- 4} } \\ { 2 } & { 5 } & { - 3 } \\ { - 5 } & { 2 } & { 4 } \end{array} \right| \\ = \color{Cerulean}{3} \color{black}{\left| \begin{array} { r r } { 5 } & { - 3 } \\ { 2 } & { 4 } \end{array} \right|} -\color{Cerulean}{ 7} \color{black}{\left| \begin{array} { c c } { 2 } & { - 3 } \\ { - 5 } & { 4 } \end{array} \right|} + ( \color{Cerulean}{- 4}\color{black}{ )} \left| \begin{array} { c c } { 2 } & { 5 } \\ { - 5 } & { 2 } \end{array} \right| \\ \begin{array} { l } { = 3 ( 20 - ( - 6 ) ) - 7 ( 8 - 15 ) - 4 ( 4 - ( - 25 ) ) } \\ { = 3 ( 26 ) - 7 ( - 7 ) - 4 ( 29 ) } \\ { = 78 + 49 - 116 } \\ { = 11 } \end{array}\)

Аналогічно ми можемо\(D_{x}, D_{y}\) обчислити і\(D_{z}\). Це залишають як вправу.

\(D _ { x } = \left| \begin{array} { c c c } { \color{Cerulean}{0} } & { \color{black}{7} } & { - 4 } \\ {\color{Cerulean}{ 1} } & { \color{black}{5} } & { - 3 } \\ {\color{Cerulean}{ 8} } & { \color{black}{2} } & { 4 } \end{array} \right| = - 44\)

\(D _ { y } = \left| \begin{array} { r r r } { 3 } & { \color{Cerulean}{0} } & { \color{black}{- 4} } \\ { 2 } & {\color{Cerulean}{ 1} } & { \color{black}{- 3} } \\ { - 5 } & { \color{Cerulean}{8} } & { \color{black}{4} } \end{array} \right| = 0\)

\(D _ { z } = \left| \begin{array} { c c c } { 3 } & { 7 } & { \color{Cerulean}{0} } \\ { 2 } & { 5 } & { \color{Cerulean}{1} } \\ { - 5 } & { 2 } & { \color{Cerulean}{8} } \end{array} \right| = - 33\)

Використовуючи правило Крамера, яке ми маємо,

\(x = \frac { D _ { x } } { D } = \frac { - 44 } { 11 } = - 4 \quad y = \frac { D _ { y } } { D } = \frac { 0 } { 11 } = 0 \quad z = \frac { D _ { z } } { D } = \frac { - 33 } { 11 } = - 3\)

Відповідь:

\((-4, 0, -3)\)

Якщо визначник матриці коефіцієнтів\(D = 0\), то система або залежна, або непослідовна. Це буде залежати від\(D_{x} , D_{y}\), і\(D_{z}\). Якщо всі вони дорівнюють нулю, значить, система залежна. Якщо хоча б один з них ненульовий, то це суперечливо.

\(\begin{array} { l } { When\:\: D = 0 \text { , } } \\ { D _ { x } = 0 \text { and } D _ { y } = 0 \text { and } D _ { z } = 0 \Rightarrow \color{Cerulean} { Dependent\: System } } \\ { D _ { x } \neq 0 \text { or } D _ { y } \neq 0 \text { or } D _ { z } \neq 0 \Rightarrow \color{Cerulean} { Inconsistent \:System } } \end{array}\)

Приклад\(\PageIndex{9}\):

Вирішіть за допомогою правила Крамера:\(\left\{ \begin{array} { c } { 4 x - y + 3 z = 5 } \\ { 21 x - 4 y + 18 z = 7 } \\ { - 9 x + y - 9 z = - 8 } \end{array} \right.\).

Рішення

Почніть з визначення відповідної доповненої матриці.

\(\left\{ \begin{array} { c } { 4 x - y + 3 z = 5 } \\ { 21 x - 4 y + 18 z = 7 } \\ { - 9 x + y - 9 z = - 8 } \end{array} \right. \Leftrightarrow \left [ \begin{array}{c c c |c } {4}& {-1} &{3} &{\color{Cerulean}{5}} \\{21} &{-4} &{18}&{\color{Cerulean}{7}} \\{-9} &{1} &{-9} &{\color{Cerulean}{-8}} \end{array} \right ]\)

Далі визначаємо детермінант матриці коефіцієнтів.

\(D = \left| \begin{array} { r r r } { \color{Cerulean}{4} } & { \color{Cerulean}{- 1} } & { \color{Cerulean}{3} } \\ { 21 } & { - 4 } & { 18 } \\ { - 9 } & { 1 } & { - 9 } \end{array} \right|\)

\(= \color{Cerulean}{4}\color{black}{ \left| \begin{array} { c c } { - 4 } & { 18 } \\ { 1 } & { - 9 } \end{array} \right|} - (\color{Cerulean}{ - 1}\color{black}{ )} \left| \begin{array} { c c } { 21 } & { 18 } \\ { - 9 } & { - 9 } \end{array} \right| + \color{Cerulean}{3}\color{black}{ \left| \begin{array} { c c } { 21 } & { - 4 } \\ { - 9 } & { 1 } \end{array} \right|}\)

\(\begin{array} { l } { = 4 ( 36 - 18 ) + 1 ( - 189 - ( - 162 ) ) + 3 ( 21 - 36 ) } \\ { = 4 ( 18 ) + 1 ( - 27 ) + 3 ( - 15 ) } \\ { = 72 - 27 - 45 } \\ { = 0 } \end{array}\)

Так як\(D=0\), система або залежна, або суперечлива.

\(D _ { x } = \left| \begin{array} { c c c} { \color{Cerulean}{5}}&{ \color{black}{- 1} } & { 3 } \\ { \color{Cerulean}{7}}&{ \color{black}{- 4} } & { 18 } \\ { \color{Cerulean}{- 8} } & { \color{black}{1}}&{ - 9 } \end{array} \right| = 96\)

Однак, оскільки\(D_{x}\) є ненульовим, ми робимо висновок, що система непослідовна. Одночасного рішення не існує.

Відповідь:

\(\varnothing\)

Вправа\(\PageIndex{3}\)

Вирішіть за допомогою правила Крамера:\(\left\{ \begin{array} { l } { 2 x + 6 y + 7 z = 4 } \\ { - 3 x - 4 y + 5 z = 12 } \\ { 5 x + 10 y - 3 z = - 13 } \end{array} \right.\).

Відповідь

\((-3, \frac{1}{2}, 1)\)

www.youtube.com/В/НФВЧГ8ОЦ

Ключові виноси

• Визначником матриці є дійсне число.
• Визначник\(2\times 2\) матриці отримують шляхом віднімання добутку значень на діагоналі.
• Визначник матриці отримують шляхом розширення\(3\times 3\) матриці за допомогою неповнолітніх щодо будь-якого рядка або стовпця. Роблячи це, подбайте про використання знакового масиву, який допоможе визначити знак коефіцієнтів.
• Використовуйте правило Крамера для ефективного визначення рішень лінійних систем.
• Коли визначник матриці коефіцієнтів є\(0\), правило Крамера не застосовується; система буде або залежною, або непослідовною.

Вправа\(\PageIndex{4}\)

Обчисліть детермінант.

1. \(\left| \begin{array} { c c } { 1}&{2 } \\ { 3}&{4 } \end{array} \right|\)
2. \(\left| \begin{array} { c c} { 5}&{3 } \\ { 2}&{4 } \end{array} \right|\)
3. \(\left| \begin{array} { c c } { - 1 } & { 3 } \\ { - 3 } & { - 2 } \end{array} \right|\)
4. \(\left| \begin{array} { c c } { 7 } & { 4 } \\ { 3 } & { - 2 } \end{array} \right|\)
5. \(\left| \begin{array} { c c} { - 4}&{1 } \\ { - 3}&{0 } \end{array} \right|\)
6. \(\left| \begin{array} { c c } { 9 } & { 5 } \\ { - 1 } & { 0 } \end{array} \right|\)
7. \(\left| \begin{array} { c c } { 1}&{0 } \\ { 5}&{0 } \end{array} \right|\)
8. \(\left| \begin{array} { c c } { 0}&{3 } \\ { 5}&{0 } \end{array} \right|\)
9. \(\left| \begin{array} { c c } { 0 } & { 4 } \\ { - 1 } & { 3 } \end{array} \right|\)
10. \(\left| \begin{array} { l l } { 10 } & { 2 } \\ { 10 } & { 2 } \end{array} \right|\)
11. \(\left| \begin{array} { l l } { a _ { 1 } } & { b _ { 1 } } \\ { 0 } & { b _ { 2 } } \end{array} \right|\)
12. \(\left| \begin{array} { l l } { 0 } & { b _ { 1 } } \\ { a _ { 2 } }&{b _ { 2 } } \end{array} \right|\)

Відповідь

1. \(-2\)

3. \(11\)

5. \(3\)

7. \(0\)

9. \(4\)

11. \(a_{1}b_{2}\)

Вправа\(\PageIndex{5}\)

Вирішіть за допомогою правила Крамера.

1. \(\left\{ \begin{array} { l } { 3 x - 5 y = 8 } \\ { 2 x - 7 y = 9 } \end{array} \right.\)
2. \(\left\{ \begin{array} { l } { 2 x + 3 y = - 1 } \\ { 3 x + 4 y = - 2 } \end{array} \right.\)
3. \(\left\{ \begin{array} { c } { 2 x - y = - 3 } \\ { 4 x + 3 y = 4 } \end{array} \right.\)
4. \(\left\{ \begin{array} { c } { x + 3 y = 1 } \\ { 5 x - 6 y = - 9 } \end{array} \right.\)
5. \(\left\{ \begin{array} { c } { x + y = 1 } \\ { 6 x + 3 y = 2 } \end{array} \right.\)
6. \(\left\{ \begin{array} { c } { x - y = - 1 } \\ { 5 x + 10 y = 4 } \end{array} \right.\)
7. \(\left\{ \begin{array} { l } { 5 x - 7 y = 14 } \\ { 4 x - 3 y = 6 } \end{array} \right.\)
8. \(\left\{ \begin{array} { l } { 9 x + 5 y = - 9 } \\ { 7 x + 2 y = - 7 } \end{array} \right.\)
9. \(\left\{ \begin{array} { c } { 6 x - 9 y = 3 } \\ { - 2 x + 3 y = 1 } \end{array} \right.\)
10. \(\left\{ \begin{array} { l } { 3 x - 9 y = 3 } \\ { 2 x - 6 y = 2 } \end{array} \right.\)
11. \(\left\{ \begin{aligned} 4 x - 5 y & = 20 \\ 3 y & = - 9 \end{aligned} \right.\)
12. \(\left\{ \begin{array} { c } { x - y = 0 } \\ { 2 x - 3 y = 0 } \end{array} \right.\)
13. \(\left\{ \begin{array} { l } { 2 x + y = a } \\ { x + y = b } \end{array} \right.\)
14. \(\left\{ \begin{aligned} a x + y & = 0 \\ b y & = 1 \end{aligned} \right.\)

Відповідь

1. \((1,-1)\)

3. \(\left( - \frac { 1 } { 2 } , 2 \right)\)

5. \(\left( - \frac { 1 } { 3 } , \frac { 4 } { 3 } \right)\)

7. \((0, -2)\)

9. \(\varnothing\)

11. \(\left( \frac { 5 } { 4 } , - 3 \right)\)

13. \(( a - b , 2 b - a )\)

Вправа\(\PageIndex{6}\)

Обчисліть детермінант.

1. \(\left| \begin{array} { c c c } { 1}&{2}&{3 } \\ { 2}&{1}&{3 } \\ { 1}&{3}&{2 } \end{array} \right|\)
2. \(\left| \begin{array} { c c c } { 2}&{5}&{1 } \\ { 1}&{2}&{4 } \\ { 3}&{2}&{3 } \end{array} \right|\)
3. \(\left| \begin{array} { r r r } { - 3 } & { 1 } & { - 1 } \\ { 3 } & { - 1 } & { - 2 } \\ { - 2 } & { 5 } & { 1 } \end{array} \right|\)
4. \(\left| \begin{array} { r r r } { 1 } & { - 1 } & { 5 } \\ { - 4 } & { 5 } & { - 1 } \\ { - 1 } & { 2 } & { - 3 } \end{array} \right|\)
5. \(\left| \begin{array} { r r r } { 3 } & { - 1 } & { 2 } \\ { 2 } & { 3 } & { - 1 } \\ { 5 } & { 2 } & { 1 } \end{array} \right|\)
6. \(\left| \begin{array} { r r r } { 4 } & { 0 } & { - 3 } \\ { 3 } & { - 1 } & { 0 } \\ { 0 } & { - 5 } & { 2 } \end{array} \right|\)
7. \(\left| \begin{array} { r r r } { 0 } & { - 3 } & { 4 } \\ { - 3 } & { 0 } & { 6 } \\ { 0 } & { 2 } & { - 3 } \end{array} \right|\)
8. \(\left| \begin{array} { c c c } { 6 } & { - 1 } & { - 3 } \\ { 2 } & { 5 } & { 2 } \\ { 8 } & { 4 } & { - 1 } \end{array} \right|\)
9. \(\left| \begin{array} { c c c } { 2}&{5}&{7 } \\ { 0}&{3}&{5 } \\ { 0}&{0}&{4 } \end{array} \right|\)
10. \(\left| \begin{array} { l l l } { 2 } & { 10 } & { 9 } \\ { 0 } & { 3 } & { 13 } \\ { 0 } & { 0 } & { 4 } \end{array} \right|\)
11. \(\left| \begin{array} { l l l } { a _ { 1 } } & { b _ { 1 }}&{ c _ { 1 } } \\ { 0}&{ b _ { 2 }}&{ c _ { 2 } } \\ { 0 } & { 0}&{ c _ { 3 } } \end{array} \right|\)
12. \(\left| \begin{array} { l l l } { a _ { 1 } } & { 0 } & { 0 } \\ { a _ { 2 } } & { b _ { 2 } } & { 0 } \\ { a _ { 3 }}&{ b _ { 3 } } & { c _ { 3 } } \end{array} \right|\)

Відповідь

1. \(6\)

3. \(-39\)

5. \(0\)

7. \(3\)

9. \(24\)

11. \(a_{1}b_{2}c_{3}\)

Вправа\(\PageIndex{7}\)

Вирішіть за допомогою правила Крамера.

1. \(\left\{ \begin{array} { c } { x - y + 2 z = - 3 } \\ { 3 x + 2 y - z = 13 } \\ { - 4 x - 3 y + z = - 18 } \end{array} \right.\)
2. \(\left\{ \begin{aligned} 3 x + 4 y - z & = 10 \\ 4 x + 6 y + 7 z & = 9 \\ 2 x + 3 y + 5 z & = 3 \end{aligned} \right.\)
3. \(\left\{ \begin{aligned} 5 x + y - z & = 0 \\ 2 x - 2 y + z & = - 9 \\ - 6 x - 5 y + 3 z & = - 13 \end{aligned} \right.\)
4. \(\left\{ \begin{array} { c } { - 4 x + 5 y + 2 z = 12 } \\ { 3 x - y - z = - 2 } \\ { 5 x + 3 y - 2 z = 5 } \end{array} \right.\)
5. \(\left\{ \begin{aligned} x - y + z & = - 1 \\ - 2 x + 4 y - 3 z & = 4 \\ 3 x - 3 y - 2 z & = 2 \end{aligned} \right.\)
6. \(\left\{ \begin{array} { l } { 2 x + y - 4 z = 7 } \\ { 2 x - 3 y + 2 z = - 4 } \\ { 4 x - 5 y + 2 z = - 5 } \end{array} \right.\)
7. \(\left\{ \begin{array} { c } { 4 x + 3 y - 2 z = 2 } \\ { 2 x + 5 y + 8 z = - 1 } \\ { x - y - 5 z = 3 } \end{array} \right.\)
8. \(\left\{ \begin{array} { c } { x - y + z = 7 } \\ { x + 2 y + z = 1 } \\ { x - 2 y - 2 z = 9 } \end{array} \right.\)
9. \(\left\{ \begin{array} { c } { 3 x - 6 y + 2 z = 12 } \\ { - 5 x - 2 y + 3 z = 4 } \\ { 7 x + 3 y - 4 z = - 6 } \end{array} \right.\)
10. \(\left\{ \begin{array} { c } { 2 x - y - 5 z = 2 } \\ { 3 x + 2 y - 4 z = - 3 } \\ { 5 x + y - 9 z = 4 } \end{array} \right.\)
11. \(\left\{ \begin{array} { l } { 4 x + 3 y - 4 z = - 13 } \\ { 2 x + 6 y - 5 z = - 2 } \\ { - 2 x - 3 y + 3 z = 5 } \end{array} \right.\)
12. \(\left\{ \begin{aligned} x - 2 y + z & = - 1 \\ 4 y - 3 z & = 0 \\ 3 y - 2 z & = 1 \end{aligned} \right.\)
13. \(\left\{ \begin{aligned} 2 x + 3 y - z & = - 5 \\ x + 2 y & = 0 \\ 3 x + 10 y & = 4 \end{aligned} \right.\)
14. \(\left\{ \begin{array} { c } { 2 x - 3 y - 2 y = 9 } \\ { - 3 x + 4 y + 4 z = - 13 } \\ { x - y - 2 z = 4 } \end{array} \right.\)
15. \(\left\{ \begin{array} { c } { 2 x + y - 2 z = - 1 } \\ { x - y + 3 z = 2 } \\ { 3 x + y - z = 1 } \end{array} \right.\)
16. \(\left\{ \begin{aligned} 3 x - 8 y + 9 z & = - 2 \\ - x + 5 y - 10 z & = 3 \\ x - 3 y + 4 z & = - 1 \end{aligned} \right.\)
17. \(\left\{ \begin{aligned} 5 x - 6 y + 3 z & = 2 \\ 3 x - 4 y + 2 z & = 0 \\ 2 x - 2 y + z & = 0 \end{aligned} \right.\)
18. \(\left\{ \begin{array} { c } { 5 x + 10 y - 4 z = 12 } \\ { 2 x + 5 y + 4 z = 0 } \\ { x + 5 y - 8 z = 6 } \end{array} \right.\)
19. \(\left\{ \begin{aligned} 5 x + 6 y + 7 z & = 2 \\ 2 y + 3 z & = 3 \\ 4 z & = 4 \end{aligned} \right.\)
20. \(\left\{ \begin{array} { c } { x + 2 z = - 1 } \\ { - 5 y + 3 z = 10 } \\ { 4 x - 3 y = 2 } \end{array} \right.\)
21. \(\left\{ \begin{array} { l } { x + y + z = a } \\ { x + 2 y + 2 z = a + b } \\ { x + 2 y + 3 z = a + b + c } \end{array} \right.\)
22. \(\left\{ \begin{array} { c } { x + y + z = a + b + c } \\ { x + 2 y + 2 z = a + 2 b + 2 c } \\ { x + y + 2 z = a + b + 2 c } \end{array} \right.\)

Відповідь

1. \((2, 3, -1)\)

3. \((-1, 2, -3)\)

5. \(\left( \frac { 1 } { 2 } , \frac { 1 } { 2 } , - 1 \right)\)

7. \((0, -2, 0)\)

9. \(\left( \frac { 1 } { 2 } z - 4 , \frac { 2 } { 3 } z + 1 , z \right)\)

11. \((-2, 1, 4)\)

13. \(\left( - \frac { 1 } { 2 } , 5 , \frac { 5 } { 2 } \right)\)

15. \(\varnothing\)

17. \((-1, 0, 1)\)

19. \(( a - b , b - c , c )\)

Вправа\(\PageIndex{8}\)

1. Досліджуйте та обговоріть історію детермінанти. Кому зараховують за перше введення позначення детермінанти?
2. Дослідіть інші способи, за допомогою яких ми можемо обчислити детермінант\(3 \times 3\) матриці. Наведіть приклад

Відповідь

1. Відповідь може відрізнятися

Виноски

²⁹ Матриця з однаковою кількістю рядків і стовпців.

³⁰ Справжнє число, пов'язане з квадратною матрицею.

³¹ Розв'язок незалежної системи лінійних рівнянь, виражених через детермінанти.

³² Визначник матриці, що виходить після усунення рядка та стовпця квадратної матриці.