11.7: Розуміння нахилу лінії (частина 1)

Цілі навчання

• Використання геобалок для моделювання схилу
• Знайти нахил прямої з її графіка
• Знайти нахил горизонтальних і вертикальних ліній
• Використовуйте формулу нахилу, щоб знайти нахил прямої між двома точками
• Графік лінії з заданою точкою і нахилом
• Вирішіть програми нахилу

будьте готові!

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

1. Спростити:$\dfrac{1 − 4}{8 − 2}$. Якщо ви пропустили цю проблему, перегляньте приклад 4.6.12.
2. Розділити:$\dfrac{0}{4}, \dfrac{4}{0}$. Якщо ви пропустили цю проблему, перегляньте приклад 7.5.5.
3. Спростити:$\dfrac{15}{-3}, \dfrac{−15}{3}, \dfrac{−15}{−3}$. Якщо ви пропустили цю проблему, перегляньте приклад 4.6.11.

Як ми були графіки лінійних рівнянь, ми бачили, що деякі лінії нахиляються вгору, як вони йдуть зліва направо і деякі лінії нахилу вниз. Деякі лінії дуже круті, а деякі лінії більш плоскі. Що визначає, чи нахиляється лінія вгору або вниз, і якщо її нахил крутий або плоский?

Крутизна ухилу лінії називається нахилом лінії. Поняття схилу має багато застосувань у реальному світі. Крок даху та клас шосе або пандуса для інвалідного візка - лише деякі приклади, в яких ви буквально бачите схили. А коли ви їдете на велосипеді, ви відчуваєте схил, коли ви накачуєте гору або берег вниз.

Використання геобалок для моделювання схилу

У цьому розділі ми вивчимо поняття схилу.

Використання гумок на геоборді дає конкретний спосіб моделювання ліній на координатній сітці. Розтягнувши гумку між двома кілочками на геоборді, ми можемо виявити, як знайти нахил лінії. А коли ви їдете на велосипеді, ви відчуваєте схил, коли ви накачуєте гору або берег вниз.

Почнемо з розтягування гумки між двома кілочками, щоб зробити лінію, як показано на малюнку$\PageIndex{1}$.

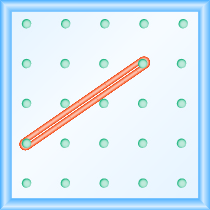
Малюнок$\PageIndex{1}$

Це схоже на лінію?

Тепер протягуємо одну частину гумки прямо вгору від лівого кілочка і навколо третього кілочка, щоб зробити сторони прямокутного трикутника, як показано на малюнку$\PageIndex{2}$. Обережно робимо кут 90° навколо третього кілочка, щоб одна сторона була вертикальною, а інша - горизонтальною.

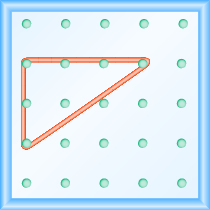
Малюнок$\PageIndex{2}$

Щоб знайти нахил лінії, заміряємо відстань по вертикальних і горизонтальних ніжках трикутника. Вертикальна відстань називається підйомом, а горизонтальна відстань називається пробігом, як показано на малюнку$\PageIndex{3}$.

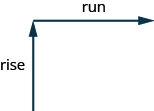
Малюнок$\PageIndex{3}$

Щоб допомогти запам'ятати терміни, це може допомогти думати про зображення, показані на малюнку$\PageIndex{4}$.

Малюнок$\PageIndex{4}$

На нашому геоборді підйом становить 2 одиниці, тому що гумка піднімається вгору 2 простору на вертикальній ніжці. Див$\PageIndex{5}$. Малюнок.

Що таке пробіг? Обов'язково підраховуйте проміжки між кілочками, а не самі кілочки! Гумка проходить через 3 простору на горизонтальній нозі, тому біг становить 3 одиниці.

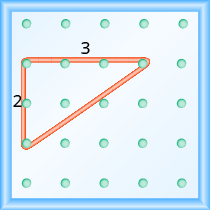
Малюнок$\PageIndex{5}$

Ухил лінії - це відношення підйому до прогону. Так що нахил нашої лінії є$\dfrac{2}{3}$. У математиці ухил завжди представлений буквою m.

Визначення: Нахил прямої

Ухил лінії m =$\dfrac{rise}{run}$.

Підйом вимірює вертикальну зміну, а пробіг вимірює зміну горизонталі.

Який нахил лінії на геоборді на малюнку$\PageIndex{5}$?

$$\begin{split} m &= \dfrac{rise}{run} \\ m &= \dfrac{2}{3} \\ The\; line\; &has\; slope\; \dfrac{2}{3} \ldotp \end{split}$$

Коли ми працюємо з геобарами, це гарна ідея, щоб отримати звичку починати з кілочка зліва і підключатися до кілочка праворуч. Потім натягуємо гумку, щоб утворився прямокутний трикутник.

Якщо ми почнемо з підняття вгору, підйом позитивний, а якщо ми розтягуємо його вниз, підйом негативний. Ми будемо вважати пробіг зліва направо, точно так само, як ви прочитали цей абзац, так що пробіг буде позитивним.

Оскільки формула нахилу має підйом над пробігом, може бути простіше завжди відрахувати підйом спочатку, а потім пробіг.

Приклад$\PageIndex{1}$:

Який нахил лінії на геоборді показаний?

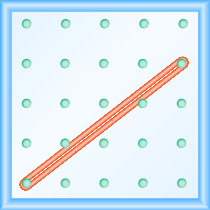
Рішення

Скористайтеся визначенням ухилу.

$$m = \dfrac{rise}{run}$$

Почніть з лівого кілочка і зробіть прямий трикутник, розтягнувши гумку вгору і вправо, щоб досягти другого кілочка. Підрахуйте підйом і пробіг, як показано на малюнку.

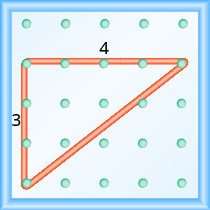
Підйом становить 3 одиниці. $$m = \dfrac{3}{run}$$

Пробіг становить 4 одиниці. $$m = \dfrac{3}{4}$$

Ухил є$\dfrac{3}{4}$.

Вправа$\PageIndex{1}$:

Який нахил лінії на геоборді показаний?

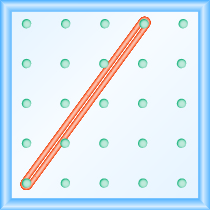
Відповідь

$\frac{4}{3}$

Вправа$\PageIndex{2}$:

Який нахил лінії на геоборді показаний?

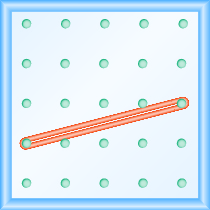
Відповідь

$\frac{1}{4}$

Приклад$\PageIndex{2}$:

Який нахил лінії на геоборді показаний?

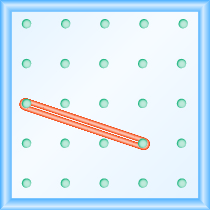
Рішення

Скористайтеся визначенням ухилу.

$$m = \dfrac{rise}{run}$$

Почніть з лівого кілочка і зробіть прямий трикутник, натягнувши гумку до кілочка праворуч. Цього разу нам потрібно розтягнути гумку вниз, щоб вийшла вертикальна нога, тому підйом негативний.

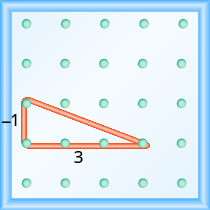
Підйом дорівнює −1.

$$m = \dfrac{−1}{run}$$

Пробіг дорівнює 3.

$$\begin{split} m &= \dfrac{−1}{3} \\ m &= − \dfrac{1}{3} \end{split}$$

Ухил є$− \dfrac{1}{3}$.

Вправа$\PageIndex{3}$:

Що таке ухил лінії на геобарді?

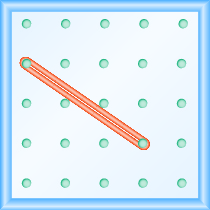
Відповідь

$-\frac{2}{3}$

Вправа$\PageIndex{4}$:

Що таке ухил лінії на геобарді?

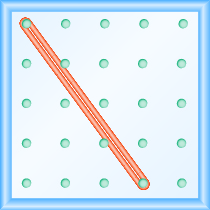
Відповідь

$-\frac{4}{3}$

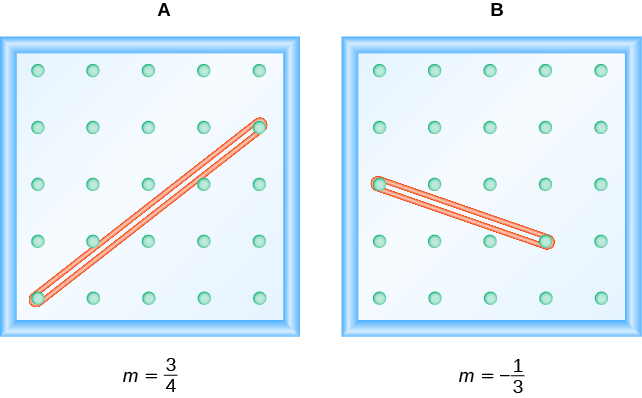
Зверніть увагу, що в першому прикладі нахил позитивний, а в другому - негативний. Чи помічаєте ви якусь різницю в двох рядках, показаних на малюнку$\PageIndex{6}$.

Малюнок$\PageIndex{6}$

Коли ви читаєте зліва направо, рядок на малюнку А піднімається вгору; вона має позитивний нахил. Лінія Рисунок B йде вниз; вона має негативний нахил.

Малюнок$\PageIndex{7}$

Приклад$\PageIndex{3}$:

Використовуйте геоборд для моделювання лінії з нахилом$\frac{1}{2}$.

Рішення

Щоб змоделювати лінію з певним ухилом на геоборді, нам потрібно знати підйом і пробіг.

Скористайтеся формулою нахилу.	$ $ м =\ dfrac {підйом} {бігти} $$
Замініть m на$\dfrac{1}{2}$.	$\ dfrac {1} {2} =\ dfrac {підйом} {бігти} $$

Отже, підйом дорівнює 1 одиниці, а пробіг - 2 одиниці.

Почніть з кілочка в лівій нижній частині геобарду. Натягуємо гумку вгору на 1 одиницю, а потім вправо 2 одиниці.

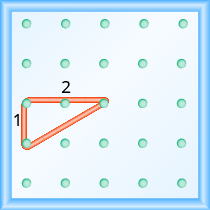
Гіпотенуза прямокутного трикутника, утвореного гумкою, являє собою лінію з нахилом$\dfrac{1}{2}$.

Вправа$\PageIndex{5}$:

Використовуйте геоборд для моделювання лінії з заданим ухилом: m =$\dfrac{1}{3}$.

Відповідь

Вправа$\PageIndex{6}$:

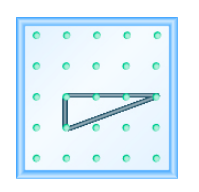
Використовуйте геоборд для моделювання лінії з заданим ухилом: m =$\dfrac{3}{2}$.

Відповідь

Приклад$\PageIndex{4}$:

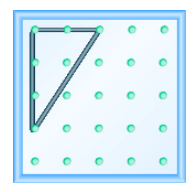
Використовуйте геоборд для моделювання лінії з нахилом$\dfrac{−1}{4}$.

Рішення

Скористайтеся формулою нахилу.	$ $ м =\ dfrac {підйом} {бігти} $$
Замініть m на$− \dfrac{1}{4}$.	$-\ dfrac {1} {4} =\ dfrac {підйом} {бігти} $$

Отже, підйом дорівнює −1, а пробіг дорівнює 4.

Оскільки підйом негативний, ми вибираємо стартовий кілочок у верхньому лівому куті, який дасть нам місце для відліку. Простягаємо гумку вниз 1 одиницю, потім вправо 4 одиниці.

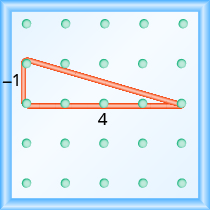
Гіпотенуза прямокутного трикутника, утвореного гумкою, являє собою лінію, нахил якої дорівнює$− \dfrac{1}{4}$.

Вправа$\PageIndex{7}$:

Використовуйте геоборд для моделювання лінії з заданим ухилом: m =$\dfrac{−3}{2}$.

Відповідь

Вправа$\PageIndex{8}$:

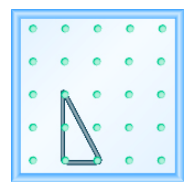
Використовуйте геоборд для моделювання лінії з заданим ухилом: m =$\dfrac{−1}{3}$.

Відповідь

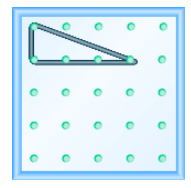
Знайти нахил прямої з її графіка

Тепер ми розглянемо деякі графіки на координатній сітці, щоб знайти їх нахили. Метод буде дуже схожий на те, що ми щойно змоделювали на наших геобордах.

Щоб знайти ухил, треба порахувати підйом і пробіг. Але з чого ми починаємо?

Знаходимо будь-які дві точки на лінії. Ми намагаємося вибирати точки з координатами, які є цілими числами, щоб полегшити наші обчислення. Потім ми починаємо з точки зліва і накидаємо прямокутний трикутник, щоб ми могли порахувати підйом і бігти.

Приклад$\PageIndex{5}$:

Знайдіть нахил показаної лінії:

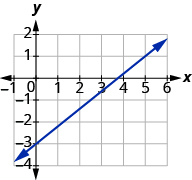
Рішення

Знайдіть дві точки на графіку, вибираючи точки, координати яких є цілими числами. Ми будемо використовувати (0, −3) і (5, 1).

Починаючи з точки зліва, (0, −3), намалюйте прямокутний трикутник, що йде від першої точки до другої точки, (5, 1).

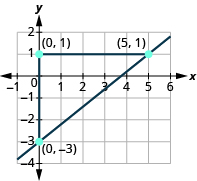
Підрахуйте підйом на вертикальній ніжці трикутника.	Підйом становить 4 одиниці.
Підрахуйте біг на горизонтальній нозі.	Пробіг становить 5 одиниць.
Скористайтеся формулою нахилу.	$ $ м =\ dfrac {підйом} {бігти} $$
Підставляємо значення підйому і бігу.	$$м =\ дфрак {4} {5}$$

Ухил лінії дорівнює$\dfrac{4}{5}$.

Зверніть увагу, що нахил є позитивним, оскільки лінія нахиляється вгору зліва направо.

Вправа$\PageIndex{9}$:

Знайдіть нахил лінії:

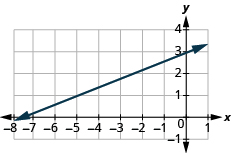
Відповідь

$\frac{2}{5}$

Вправа$\PageIndex{10}$:

Знайдіть нахил лінії:

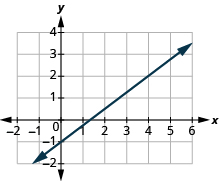
Відповідь

$\frac{3}{4}$

ЯК: ЗНАЙТИ УХИЛ ЗА ГРАФІКОМ

Крок 1. Знайдіть дві точки на лінії, координати яких є цілими числами.

Крок 2. Починаючи з точки зліва, накидайте прямокутний трикутник, що йде від першої точки до другої точки.

Крок 3. Підрахуйте підйом і біг на ніжках трикутника.

Крок 4. Візьміть співвідношення підйому до бігу, щоб знайти схил.

$$m = \dfrac{rise}{run}$$

Приклад$\PageIndex{6}$:

Знайдіть нахил показаної лінії:

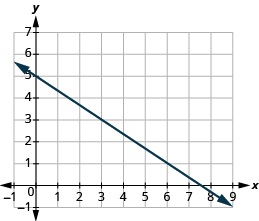
Рішення

Знайдіть дві точки на графіку. Шукайте точки з координатами, які є цілими числами. Ми можемо вибрати будь-які точки, але будемо використовувати (0, 5) і (3, 3). Починаючи з точки зліва, накидайте прямокутний трикутник, що йде від першої точки до другої точки.

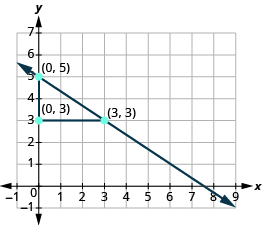
Підрахуйте підйом — він негативний.	Підйом дорівнює −2.
Підрахуйте пробіг.	Пробіг дорівнює 3.
Скористайтеся формулою нахилу.	$ $ м =\ dfrac {підйом} {бігти} $$
Підставляємо значення підйому і бігу.	$$м =\ дфрак {-2} {3}$$
Спростити.	$$м = -\ дфрак {2} {3}$$

Ухил лінії дорівнює$− \dfrac{2}{3}$.

Зверніть увагу, що нахил негативний, оскільки лінія нахиляється вниз зліва направо.

Що робити, якщо ми обрали різні моменти? Давайте знову знайдемо нахил лінії, на цей раз використовуючи різні точки. Ми будемо використовувати точки (−3, 7) і (6, 1).

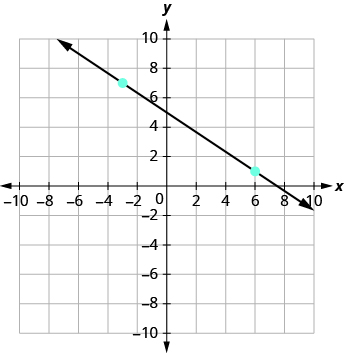
Починаючи з (−3, 7), намалюйте прямокутний трикутник до (6, 1).

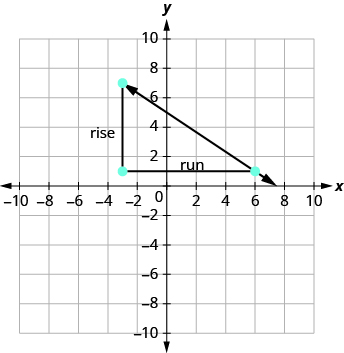
Підрахуйте підйом.	Підйом дорівнює −6.
Підрахуйте пробіг.	Пробіг - 9.
Скористайтеся формулою нахилу.	$ $ м =\ dfrac {підйом} {бігти} $$
Підставляємо значення підйому і бігу.	$$м =\ дфрак {-6} {9}$$
Спростити дріб.	$$м = -\ дфрак {2} {3}$$

Ухил лінії дорівнює$− \dfrac{2}{3}$.

Не має значення, які точки ви використовуєте - нахил лінії завжди однаковий. Нахил лінії постійний!

Вправа$\PageIndex{11}$:

Знайдіть нахил лінії:

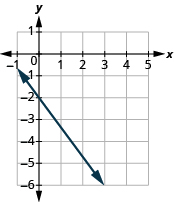
Відповідь

$-\frac{4}{3}$

Вправа$\PageIndex{12}$:

Знайдіть нахил лінії:

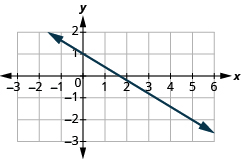
Відповідь

$-\frac{3}{5}$

Рядки в попередніх прикладах мали y-перехоплення з цілими значеннями, тому було зручно використовувати y-перехоплення як одну з точок, які ми використовували для пошуку нахилу. У наступному прикладі y-перехоплення - це дріб. Обчислення простіше, якщо ми використовуємо дві точки з цілочисельними координатами.

Приклад$\PageIndex{7}$:

Знайдіть нахил показаної лінії:

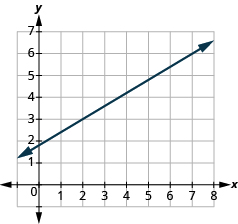
Рішення

Знайдіть дві точки на графіку, координати яких є цілими числами.	(2, 3) і (7, 6)
Яка точка знаходиться зліва?	(2, 3)

Починаючи з (2, 3), намалюйте прямий кут до (7, 6), як показано нижче.

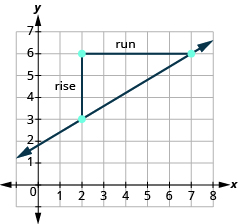
Підрахуйте підйом.	Підйом дорівнює 3.
Підрахуйте пробіг.	Пробіг дорівнює 5.
Скористайтеся формулою нахилу.	$ $ м =\ dfrac {підйом} {бігти} $$
Підставляємо значення підйому і бігу.	$$м =\ дфрак {3} {5}$$

Ухил лінії дорівнює$\dfrac{3}{5}$.

Вправа$\PageIndex{13}$:

Знайдіть нахил лінії:

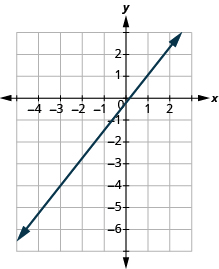
Відповідь

$\frac{5}{4}$

Вправа$\PageIndex{14}$:

Знайдіть нахил лінії:

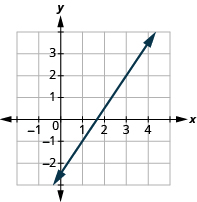
Відповідь

$\frac{3}{2}$

Знайти нахил горизонтальних і вертикальних ліній

Ви пам'ятаєте, що особливого було в горизонтальних і вертикальних лініях? Їх рівняння мали лише одну змінну.

• горизонтальна лінія y = b; всі y -координати однакові.
• вертикальна лінія x = a; всі x -координати однакові.

Так як же знайти нахил горизонтальної лінії y = 4? Одним з підходів було б намалювати горизонтальну лінію, знайти дві точки на ній і підрахувати підйом і пробіг. Давайте подивимося, що відбувається на малюнку$\PageIndex{8}$. Ми будемо використовувати дві точки (0, 4) і (3, 4), щоб підрахувати підйом і бігти.

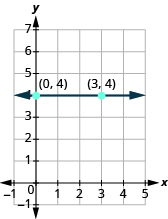
Малюнок$\PageIndex{8}$

Що таке підйом?	Підйом дорівнює 0.
Що таке пробіг?	Пробіг дорівнює 3.
Що таке ухил?	$$m =\ dfrac {підйом} {запустити}\ тег {11.4.21}$$
	$$m =\ дфрак {0} {3}\ тег {11.4.22}$$
	$m = 0\ тег {11.4.23} $$

Ухил горизонтальної лінії y = 4 дорівнює 0.

Всі горизонтальні лінії мають нахил 0. Коли y-координати однакові, підйом дорівнює 0.

Визначення: Нахил горизонтальної лінії

Ухил горизонтальної лінії, y = b, дорівнює 0.

Тепер розглянемо вертикальну лінію, таку як лінія х = 3, показана на малюнку$\PageIndex{9}$. Ми будемо використовувати дві точки (3, 0) і (3, 2), щоб підрахувати підйом і бігти.

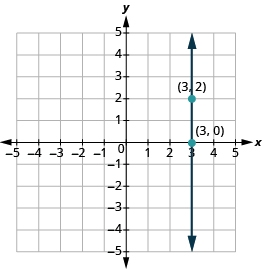
Малюнок$\PageIndex{9}$

Що таке підйом?	Підйом дорівнює 2.
Що таке пробіг?	Прогін дорівнює 0.
Що таке ухил?	$$m =\ dfrac {підйом} {запустити}\ тег {11.4.24}$$
	$$m =\ дфрак {2} {0}\ тег {11.4.25}$$

Але ми не можемо розділити на 0. Ділення на 0 не визначено. Так ми говоримо, що нахил вертикальної лінії х = 3 невизначений. Нахил всіх вертикальних ліній не визначено, оскільки прогін дорівнює 0.

Визначення: Нахил вертикальної лінії

Нахил вертикальної лінії, x = a, не визначено.

Приклад$\PageIndex{8}$:

Знайти нахил кожного рядка: (a) x = 8 (b) y = −5

Рішення

(а) х = 8

Це вертикальна лінія, тому її нахил невизначений.

(б) у = −5

Це горизонтальна лінія, тому її нахил дорівнює 0.

Вправа$\PageIndex{15}$:

Знайти нахил прямої: x = −4.

Відповідь

невизначений

Вправа$\PageIndex{16}$:

Знайдіть ухил лінії: y = 7.

Відповідь

0

Короткий посібник по схилах ліній

Використовуйте формулу нахилу, щоб знайти нахил лінії між двома точками

Іноді нам потрібно знайти нахил лінії між двома точками, і ми можемо не мати графіка, щоб відрахувати підйом і пробіг. Ми могли б намітити точки на сітковому папері, потім порахувати підйом і пробіг, але є спосіб знайти схил без графіків.

Перш ніж ми перейдемо до нього, нам потрібно ввести деякі нові алгебраїчні позначення. Ми бачили, що впорядкована пара (x, y) дає координати точки. Але коли ми працюємо з ухилами, використовуємо дві точки. Як можна використовувати один і той же символ (x, y) для представлення двох різних точок?

Математики використовують індекси, щоб розрізняти точки. Індекс - це невелике число, записане праворуч від змінної, і трохи нижче, ніж.

• (х ₁, у ₁) читати х суб 1, у суб 1
• (х ₂, у ₂) читати х суб 2, у суб 2

Ми будемо використовувати (x ₁, y ₁) для ідентифікації першої точки і (x ₂, y ₂) для ідентифікації другої точки. Якби у нас було більше двох точок, ми могли б використовувати (x ₃, y ₃), (x ₄, y ₄), і так далі.

Щоб побачити, як підйом і пробіг співвідносяться з координатами двох точок, давайте ще раз подивимося на нахил лінії між точками (2, 3) і (7, 6) на малюнку$\PageIndex{10}$.

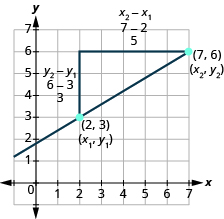
Малюнок$\PageIndex{10}$

Так як у нас дві точки, ми будемо використовувати індексні позначення.

$$\begin{split} x_{1}, y_{1} \qquad &x_{2}, y_{2} \\ (2, 3) \qquad &(7, 6) \end{split}$$

На графіку ми порахували підйом 3. Підйом також можна знайти, віднімаючи y-координати точок.

$$\begin{split} y_{2} &- y_{1} \\ 6 &- 3 \\ &\; 3 \end{split}$$

Ми порахували пробіг 5. Прогін також можна знайти, віднімаючи x-координати.

$$\begin{split} x_{2} &- x_{1} \\ 7 &- 2 \\ &\; 5 \end{split}$$

Ми знаємо	$$m =\ dfrac {підйом} {запустити}\ тег {11.4.26}$$
Так	$$m =\ дфрак {3} {5}\ тег {11.4.27}$$
Переписуємо підйом і біжимо, вставивши координати.	$$m =\ дфрак {6 - 3} {7 - 2}\ тег {11.4.28}$$
Але 6 - y-координата другої точки, y 2 і 3 - y-координата першої точки y 1. Таким чином, ми можемо переписати підйом за допомогою індексу позначення.	$$м =\ dfrac {y_ {2} - y_ {1}} {7 - 2}\ тег {11.4.29}$$
Також 7 - координата x другої точки, x 2 і 2 - координата x першої точки x 2. Таким чином, ми переписуємо прогін, використовуючи індексні позначення.	$$м =\ дфрак {y_ {2} - y_ {1}} {x_ {2} - x_ {1}}\ тег {11.4.30}$$

Ми показали, що m =$\dfrac{y_{2} − y_{1}}{x_{2} − x_{1}}$ дійсно інша версія m =$\dfrac{rise}{run}$. Ми можемо використовувати цю формулу, щоб знайти нахил прямої, коли у нас є дві точки на лінії.

Визначення: Формула нахилу

Нахил лінії між двома точками (x ₁, y ₁) і (x ₂, y ₂) дорівнює

$$m = \dfrac{y_{2} - y_{1}}{x_{2} - x_{1}} \tag{11.4.31}$$

Скажіть формулу собі, щоб допомогти вам її запам'ятати:

Ухил - y другої точки мінус y першої точки

над

x другої точки мінус х першої точки.

Приклад$\PageIndex{9}$:

Знайдіть нахил лінії між точками (1, 2) і (4, 5).

Рішення

Ми назвемо (1, 2) точку #1 і (4, 5) точку #2.	$\ почати {спліт} x_ {1}, y_ {1}\ qquad &x_ {2}, y_ {2}\\ (1, 2)\ qquad & (4, 5)\ кінець {спліт} $$
Скористайтеся формулою нахилу.	$$м =\ дфрак {y_ {2} - y_ {1}} {x_ {2} - x_ {1}}\ тег {11.4.32}$$
Підставляємо значення в формулу нахилу:
y другої точки мінус y першої точки	$$м =\ дфрак {5 - 2} {x_ {2} - x_ {1}}\ тег {11.4.33}$$
x другої точки мінус х першої точки	$$m =\ дфрак {5 - 2} {4 - 1}\ тег {11.4.34}$$
Спростити чисельник і знаменник.	$$m =\ дфрак {3} {3}\ тег {11.4.35}$$
	м = 1

Підтвердимо це підрахунком нахилу на графіку.

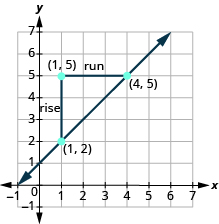
Підйом дорівнює 3, а пробіг - 3, тому

$$\begin{split} m &= \dfrac{rise}{run} \\ m &= \dfrac{3}{3} \\ m &= 1 \end{split}$$

Вправа$\PageIndex{17}$:

Знайти нахил прямої через задані точки: (8, 5) і (6, 3).

Відповідь

1

Вправа$\PageIndex{18}$:

Знайти нахил прямої через задані точки: (1, 5) і (5, 9).

Відповідь

1

Як ми знаємо, в яку точку зателефонувати #1, а яку зателефонувати #2? Давайте знову знайдемо нахил, на цей раз перемикаючи назви точок, щоб побачити, що відбувається. Так як ми зараз будемо рахувати пробіг справа наліво, то він буде негативним.

Ми будемо називати (4, 5) точку #1 і (1, 2) точку #2.	$\ почати {спліт} x_ {1}, y_ {1}\ qquad &x_ {2}, y_ {2}\\ (4, 5)\ qquad & (1, 2)\ кінець {спліт} $$
Скористайтеся формулою нахилу.	$$м =\ дфрак {y_ {2} - y_ {1}} {x_ {2} - x_ {1}}\ тег {11.4.36}$$
Підставляємо значення в формулу нахилу:
y другої точки мінус y першої точки	$$м =\ дфрак {2 - 5} {x_ {2} - x_ {1}}\ тег {11.4.37}$$
x другої точки мінус х першої точки	$$m =\ дфрак {2 - 5} {1 - 4}\ тег {11.4.38}$$
Спростити чисельник і знаменник.	$$m =\ дфрак {-3} {-3}\ тег {11.4.39}$$
	м = 1

Нахил однаковий незалежно від того, в якому порядку ми використовуємо точки.

Приклад$\PageIndex{10}$:

Знайти нахил прямої через точки (−2, −3) та (−7, 4).

Рішення

Ми назвемо (−2, −3) точку #1 і (−7, 4) точку #2.	$\ почати {спліт} x_ {1}, y_ {1}\ qquad &x_ {2}, y_ {2}\\ (-2, -3)\ qquad & (-7, 4)\ кінець {спліт} $$
Скористайтеся формулою нахилу.	$$м =\ дфрак {y_ {2} - y_ {1}} {x_ {2} - x_ {1}}\ тег {11.4.40}$$
Підставляємо значення.
y другої точки мінус y першої точки	$$м =\ дфрак {4 - (-3)} {x_ {2} - x_ {1}}\ тег {11.4.41}$$
x другої точки мінус х першої точки	$$m =\ dfrac {4 - (-3)} {-7 - (-2)}\ тег {11.4.42}$$
Спростити.	$$m =\ дфрак {7} {-5}\ тег {11.4.43}$$
	м =$- \dfrac{7}{5}$

Підтвердимо це на показаному графіку.

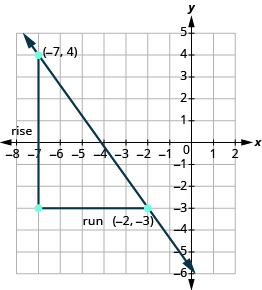
$$\begin{split} m &= \dfrac{rise}{run} \\ m &= \dfrac{-7}{5} \\ m &= - \dfrac{7}{5} \end{split}$$

Вправа$\PageIndex{19}$:

Знайти нахил прямої через пару точок: (−3, 4) і (2, −1).

Відповідь

-1

Вправа$\PageIndex{20}$:

Знайти нахил прямої через пару точок: (−2, 6) та (−3, −4).

Відповідь

10

Дописувачі та атрибуція

• Template:ContribOpenStaxPreAlgebra