Skip to main content
LibreTexts - Ukrayinska

11.4: Графічні лінійні рівняння (частина 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    57793

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Графік Вертикальні та горизонтальні лінії

    Чи можемо ми графувати рівняння лише з однією змінною? Просто х і ні у, або просто у без х? Як ми будемо складати таблицю значень, щоб отримати точки для побудови?

    Розглянемо рівняння x = −3. Рівняння говорить, що x завжди дорівнює −3, тому його значення не залежить від y. Незалежно від y, значення x завжди дорівнює −3.

    Щоб скласти таблицю розв'язків, ми запишемо −3 для всіх значень x. Потім виберіть будь-які значення для y, оскільки x не залежить від y, ви можете вибрати будь-які числа, які вам подобаються. Але щоб відповідати розміру нашого координатного графіка, ми будемо використовувати 1, 2 і 3 для y-координат, як показано в таблиці.

    х = -3
    х у (х, у)
    -3 1 (-3, 1)
    -3 2 (-3, 2)
    -3 3 (-3, 3)

    Потім намітьте точки і з'єднайте їх прямою лінією. Зверніть увагу на малюнку\(\PageIndex{5}\), що графік є вертикальною лінією.

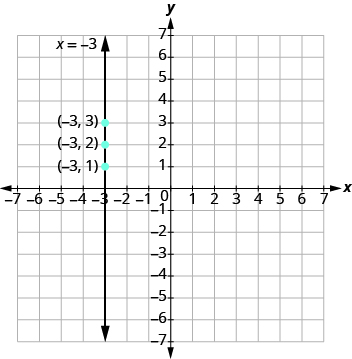
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Вертикальна лінія проходить через три мічені точки: «впорядкована пара -3, 3», «впорядкована пара -3, 2» та впорядкована пара -3, 1». Рядок позначається x = -3.

    Малюнок\(\PageIndex{5}\)

    Визначення: Вертикальна лінія

    Вертикальна лінія - це графік рівняння, який можна записати у вигляді x = a. лінія проходить через вісь x в (a, 0).

    Приклад\(\PageIndex{6}\):

    Графік рівняння х = 2. Який тип лінії вона утворює?

    Рішення

    Рівняння має тільки змінну, x і x завжди дорівнює 2. Ми робимо таблицю, де х завжди 2 і ставимо в будь-які значення для y.

    х = -3
    х у (х, у)
    2 1 (2, 1)
    2 2 (2, 2)
    2 3 (2, 3)

    Помістіть точки і з'єднайте їх, як показано на малюнку.

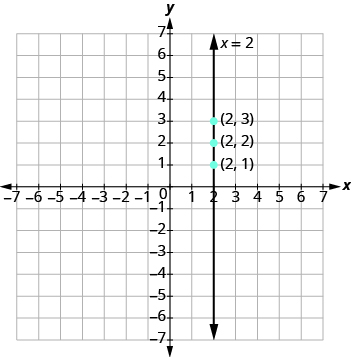
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Вертикальна лінія проходить через три мічені точки, «впорядкована пара 2, 3», «впорядкована пара 2, 2», і впорядкована пара 2, 1». Рядок позначається x = 2.

    Графік являє собою вертикальну лінію, що проходить через вісь x на 2.

    Вправа\(\PageIndex{10}\):

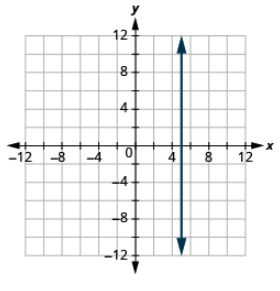
    Графік рівняння: x = 5.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Вертикальна лінія проходить через точки «впорядкована пара 5, 0» і «впорядкована пара 5, 1».

    Вправа\(\PageIndex{11}\):

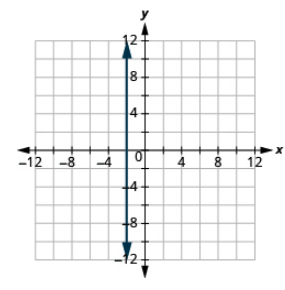
    Графік рівняння: x = −2.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Вертикальна лінія проходить через точки «впорядкована пара -2, 0» і «впорядкована пара -2, 1».

    Що робити, якщо рівняння має y, але немає x? Давайте проведемо графік рівняння y = 4. На цей раз y -значення є постійною, тому в цьому рівнянні y не залежить від x.

    Щоб скласти таблицю розв'язків, напишіть 4 для всіх значень y, а потім виберіть будь-які значення для x.

    Ми будемо використовувати 0, 2 і 4 для х -значення.

    х = -3
    х у (х, у)
    0 4 (0, 4)
    2 4 (2, 4)
    4 4 (4, 4)

    Намалюйте точки і з'єднайте їх, як показано на малюнку\(\PageIndex{6}\). Цей графік є горизонтальною лінією, що проходить через вісь y на 4.

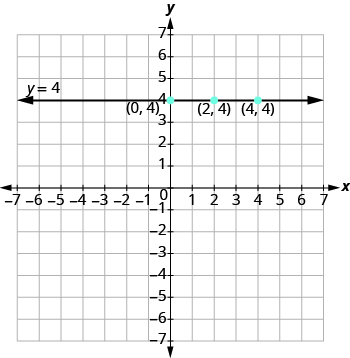
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Горизонтальна лінія проходить через три мічені точки: «впорядкована пара 0, 4», «впорядкована пара 2, 4», і впорядкована пара 4, 4». Рядок позначається y = 4.

    Малюнок\(\PageIndex{6}\)

    Визначення: Горизонтальна лінія

    Горизонтальна лінія - це графік рівняння, яке можна записати у вигляді y = b. лінія проходить через вісь y в (0, b).

    Приклад\(\PageIndex{7}\):

    Графік рівняння y = −1.

    Рішення

    Рівняння y = −1 має лише змінну, y. Значення y є постійним. Усі впорядковані пари в таблиці мають однакову y -координату, −1. Ми вибираємо значення 0, 3 та −3 як значення для x.

    х = -3
    х у (х, у)
    -3 -1 (-3, -1)
    0 -1 (0, -1)
    3 -1 (3, -1)

    Графік являє собою горизонтальну лінію, що проходить через вісь y з —1, як показано на малюнку.

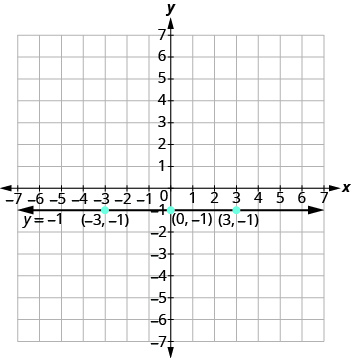
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Горизонтальна лінія проходить через три мічені точки: «впорядкована пара -3, -1», «впорядкована пара 0, -1» та впорядкована пара 3, -1». Рядок позначається y = -1.

    Вправа\(\PageIndex{12}\):

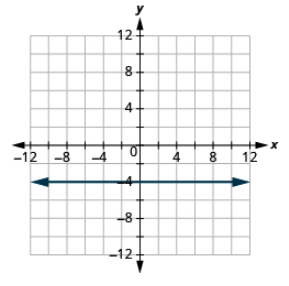
    Графік рівняння: y = −4.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Горизонтальна лінія проходить через точки «впорядкована пара 0, -4» і «впорядкована пара 1, -4».

    Вправа\(\PageIndex{13}\):

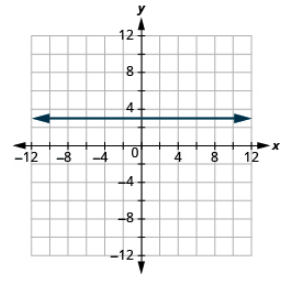
    Графік рівняння: y = 3.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Горизонтальна лінія проходить через точки «впорядкована пара 0, 3» і «впорядкована пара 1, 3».

    Рівняння для вертикальних і горизонтальних ліній виглядають дуже схожими на рівняння типу y = 4x. У чому різниця рівнянь y = 4x і y = 4?

    Рівняння y = 4x має і x, і y. Значення y залежить від значення x. Y-координата змінюється відповідно до значення x.

    Рівняння y = 4 має тільки одну змінну. Значення y постійне. Y-координата завжди дорівнює 4. Вона не залежить від значення х.

    у = 4х
    х у (х, у)
    0 0 (0, 0)
    1 4 (1, 4)
    2 8 (2, 8)
    \(\textcolor{red}{y = 4}\)
    \ (\ textcolor {червоний} {y = 4}\) "> x у (х, у)
    \ (\ колір тексту {червоний} {y = 4}\) "> 0 4 (0, 4)
    \ (\ колір тексту {червоний} {y = 4}\) "> 1 4 (1, 4)
    \ (\ колір тексту {червоний} {y = 4}\) "> 2 4 (2, 4)

    На графіку показано обидва рівняння.

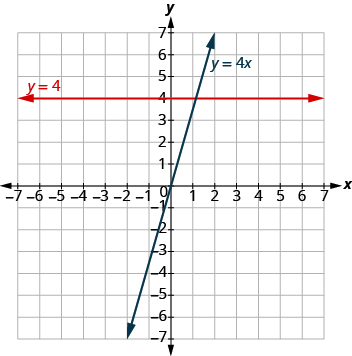
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Горизонтальна лінія проходить через «впорядковану пару 0, 4» і «впорядковану пару 1, 4» і позначається y = 4. Другий рядок проходить через «впорядковану пару 0, 0» і «впорядковану пару 1, 4» і позначається y = 4 x. Два рядки перетинаються на «впорядкованій парі 1, 4».

    Зверніть увагу, що рівняння y = 4x дає похилу лінію, тоді як y = 4 дає горизонтальну лінію.

    Приклад\(\PageIndex{8}\):

    Графік y = −3x та y = −3 у тій самій прямокутній системі координат.

    Рішення

    Знайдіть три рішення для кожного рівняння. Зверніть увагу, що перше рівняння має змінну x, а друге - ні. Наведено розв'язки для обох рівнянь.

    \(\textcolor{red}{y = -3x}\)
    \ (\ textcolor {червоний} {y = -3x}\) "> x у (х, у)
    \ (\ колір тексту {червоний} {y = -3x}\) "> 0 0 (0, 0)
    \ (\ колір тексту {червоний} {y = -3x}\) "> 1 -3 (1, -3)
    \ (\ колір тексту {червоний} {y = -3x}\) "> 2 -6 (2, -6)
    у = -3
    х у (х, у)
    0 -3 (0, -3)
    1 -3 (1, -3)
    2 -3 (2, -3)

    На графіку показано обидва рівняння.

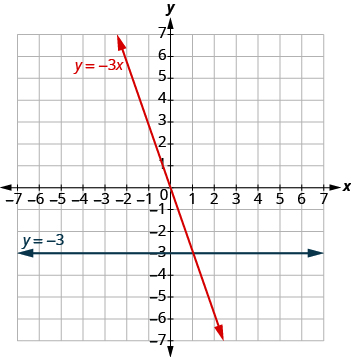
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -7 до 7. Горизонтальна лінія проходить через «впорядковану пару 0, -3» і «впорядковану пару 1, -3» і маркується y = -3. Другий рядок проходить через «впорядковану пару 0, 0» і «впорядковану пару 1, -3» і позначається y = -3 x. Два рядки перетинаються на «впорядкованій парі 1, -3».

    Вправа\(\PageIndex{14}\):

    Графік рівнянь у тій самій прямокутній системі координат: y = −4x та y = −4.

    Відповідь

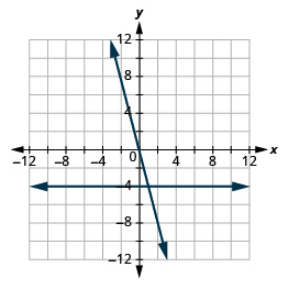
    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Горизонтальна лінія проходить через «впорядковану пару 0, -4» і «впорядковану пару 1, -4». Другий рядок проходить через «впорядковану пару 0, 0» та «впорядковану пару 1, -4». Дві лінії перетинаються на «впорядкованій парі 1, -4».

    Вправа\(\PageIndex{15}\):

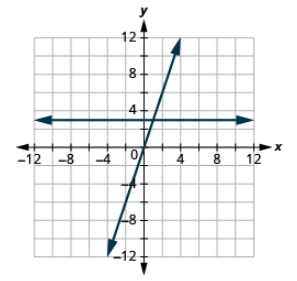
    Графік рівнянь в тій же прямокутній системі координат: y = 3 і y = 3x.

    Відповідь

    На графіку показана координатна площина x y. По осі x і y кожна проходить від -12 до 12. Горизонтальна лінія проходить через «впорядковану пару 0, 3» і «впорядковану пару 1, 3». Другий рядок проходить через «впорядковану пару 0, 0» та «впорядковану пару 1, 3». Дві лінії перетинаються на «впорядкованій парі 1, 3».

    ДОСТУП ДО ДОДАТКОВИХ ОНЛАЙН-РЕСУРСІВ

    Використання таблиці значень

    Графік лінійного рівняння за участю дробів

    Графік горизонтальних і вертикальних ліній

    Практика робить досконалим

    Визнати зв'язок між розв'язками рівняння та його графіком

    Для кожної впорядкованої пари вирішуйте (а) чи є впорядкована пара рішенням рівняння? (б) точка на лінії?

    1. у = х + 2
      1. (0, 2)
      2. (1, 2)
      3. (− 1, 1)
      4. (− 3, 1)
    2. y = х − 4
      1. (0, − 4)
      2. (3, − 1)
      3. (2, 2)
      4. (1, − 5)
    3. y =\(\dfrac{1}{2}\) х − 3
      1. (0, − 3)
      2. (2, − 2)
      3. (− 2, − 4)
      4. (4, 1)
    4. у =\(\dfrac{1}{3}\) х + 2
      1. (0, 2)
      2. (3, 3)
      3. (− 3,2)
      4. (− 6,0)

    Графік лінійного рівняння шляхом побудови точок

    У наступних вправах граф за допомогою побудови точок.

    1. y = 3x − 1
    2. у = 2х+ 3
    3. y = −2х + 2
    4. y = −3х + 1
    5. у = х + 2
    6. y = х − 3
    7. y = − x − 3
    8. y = − x − 2
    9. у = 2х
    10. у = 3х
    11. y = −4х
    12. y = −2х
    13. у =\(\dfrac{1}{2}\) х + 2
    14. y =\(\dfrac{1}{3}\) х − 1
    15. y =\(\dfrac{4}{3}\) х − 5
    16. y =\(\dfrac{3}{2}\) х − 3
    17. у =\(− \dfrac{2}{5}\) х + 1
    18. y =\(− \dfrac{4}{5}\) х − 1
    19. у =\(− \dfrac{3}{2}\) х + 2
    20. у =\(− \dfrac{5}{3}\) х + 4
    21. х + у = 6
    22. х + у = 4
    23. х + у = −3
    24. х + у = −2
    25. x × y = 2
    26. x × y = 1
    27. x − y = −1
    28. x − y = −3
    29. −х + у = 4
    30. −х + у = 3
    31. −x − у = 5
    32. −x − у = 1
    33. 3х+ у = 7
    34. 5х+ у = 6
    35. 2х+ у = −3
    36. 4х+ у = −5
    37. 2х+ 3г = 12
    38. 3х− 4вх = 12
    39. \(\dfrac{1}{3}\)х + у = 2
    40. \(\dfrac{1}{2}\)х + у = 3

    Графік Вертикальні та Горизонтальні лінії

    У наступних вправах проведіть графік вертикальної і горизонтальної ліній.

    1. х = 4
    2. х = 3
    3. х = −2
    4. х = −5
    5. у = 3
    6. у = 1
    7. y = −5
    8. y = −2
    9. х =\(\dfrac{7}{3}\)
    10. х =\(\dfrac{5}{4}\)

    У наступних вправах графік кожної пари рівнянь в одній і тій же прямокутній системі координат.

    1. у =\(− \dfrac{1}{2}\) х і у =\(− \dfrac{1}{2}\)
    2. у =\(− \dfrac{1}{3}\) х і у =\(− \dfrac{1}{3}\)
    3. у = 2х і у = 2
    4. у = 5х і у = 5

    Змішана практика

    У наступних вправах проведіть графік кожного рівняння.

    1. у = 4х
    2. у = 2х
    3. у =\(− \dfrac{1}{2}\) х + 3
    4. y =\(\dfrac{1}{4}\) х − 2
    5. y = − х
    6. у = х
    7. x × y = 3
    8. х + у = − 5
    9. 4х + у = 2
    10. 2х+ у = 6
    11. y = −1
    12. у = 5
    13. 2х+ 6р = 12
    14. 5х+ 2г = 10
    15. х = 3
    16. х = −4

    Щоденна математика

    1. Вартість будинку на автомобілі Робінзони орендували будинок на один тиждень, щоб поїхати у відпустку. Це коштувало їм $594 плюс $0.32 за милю, щоб орендувати будинок двигуна, тому лінійне рівняння y = 594+ 0,32x дає вартість, y, для водіння х миль. Розрахуйте вартість прокату за проїзд 400, 800 і 1200 миль, а потім проведіть графік лінії.
    2. Щотижневий заробіток У художній галереї, де він працює, Сальвадору платять 200 доларів на тиждень плюс 15% продажів, які він робить, тому рівняння y = 200+ 0,15x дає суму y, яку він заробляє за продаж х доларів художніх робіт. Обчисліть суму, яку Сальвадор заробляє за продаж $900, 1600 і $2,000, а потім графік лінії.

    Письмові вправи

    1. Поясніть, як вибрати три значення x, щоб скласти таблицю для графіка лінії y =\(\dfrac{1}{5}\) x − 2.
    2. У чому різниця між рівняннями вертикальної і горизонтальної лінії?

    Самостійна перевірка

    (а) Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

    CNX_BMath_Figure_AppB_067.jpg

    (b) Ознайомившись з цим контрольним списком, що ви робите, щоб стати впевненими у всіх цілях?

    Автори та атрибуція