10.10: Вступ до факторингових поліномів

Цілі навчання

• Знайдіть найбільший спільний коефіцієнт двох або більше виразів
• Фактор найбільший спільний фактор з полінома

будьте готові!

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

1. Фактор 56 в простих чисел. Якщо ви пропустили цю проблему, перегляньте приклад 2.9.1.
2. Помножте: −3 (6a + 11). Якщо ви пропустили цю проблему, перегляньте приклад 7.4.9.
3. Множимо: 4x ² (x ² + 3x − 1). Якщо ви пропустили цю проблему, перегляньте приклад 10.4.5.

Знайдіть найбільший спільний фактор двох або більше виразів

Раніше ми множили коефіцієнти разом, щоб отримати продукт. Тепер ми змінимо цей процес; ми почнемо з продукту, а потім розбиваємо його на фактори. Розбиття продукту на фактори називається факторингом.

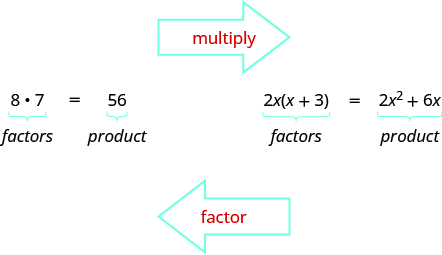
У Мові алгебри ми враховували числа, щоб знайти найменш поширене кратне (LCM) двох або більше чисел. Тепер ми будемо факторні вирази і знайдемо найбільший спільний фактор двох або більше виразів. Метод, який ми використовуємо, схожий на те, що ми використовували для пошуку LCM.

Визначення: Найбільший спільний фактор

Найбільшим загальним фактором (GCF) двох і більше виразів є найбільший вираз, який є фактором всіх виразів.

Спочатку знайдемо найбільший спільний множник двох чисел

Приклад\(\PageIndex{1}\):

Знайдіть найбільший спільний коефіцієнт 24 і 36.

Рішення

Крок 1: Розподіліть кожен коефіцієнт на прості числа. Запишіть всі змінні з показниками в розгорнутому вигляді.	Фактор 24 і 36.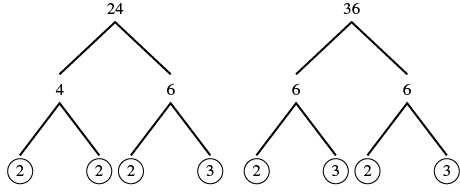
Крок 2: Перерахуйте всі фактори - відповідні загальні фактори у стовпці.
У кожному стовпці обведіть загальні фактори.	Обведіть 2, 2 та 3, які поділяються обома числами.
Крок 3: Збийте загальні фактори, які поділяють всі вирази.	Збийте 2, 2, 3, а потім помножте.
Крок 4: Помножте коефіцієнти.		ЗКФ 24 і 36 дорівнює 12.

Зверніть увагу, що оскільки GCF є коефіцієнтом обох чисел, 24 і 36 можуть бути записані як кратні 12.

\[\begin{split} 24 &= 12 \cdot 2 \\ 36 &= 12 \cdot 3 \end{split}\]

Вправа\(\PageIndex{1}\):

Знайдіть найбільший спільний фактор: 54, 36.

Відповідь

18

Вправа\(\PageIndex{2}\):

Знайдіть найбільший спільний фактор: 48, 80.

Відповідь

16

У попередньому прикладі ми знайшли найбільший спільний коефіцієнт констант. Найбільший спільний фактор алгебраїчного виразу може містити змінні, підняті до степенів разом з коефіцієнтами. Ми підсумовуємо кроки, які ми використовуємо, щоб знайти найбільший загальний фактор.

ЯК: ЗНАЙТИ НАЙБІЛЬШИЙ ЗАГАЛЬНИЙ ФАКТОР

Крок 1. Розподіл кожного коефіцієнта на простих чисел. Запишіть всі змінні з показниками в розгорнутому вигляді.

Крок 2. Перелічити всі фактори, що відповідають загальним факторам у стовпці. У кожному стовпці обведіть загальні фактори.

Крок 3. Збийте загальні фактори, які поділяють всі вирази.

Крок 4. Помножте коефіцієнти.

Приклад\(\PageIndex{2}\):

Знайдіть найбільший загальний коефіцієнт 5x і 15.

Рішення

Розподіліть кожне число в простих чисел. Обведіть загальні фактори в кожному стовпці. Збийте загальні фактори.

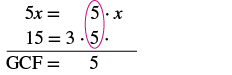GCF 5x і 15 дорівнює 5.

Вправа\(\PageIndex{3}\):

Знайдіть найбільший спільний фактор: 7y, 14.

Відповідь

7

Вправа\(\PageIndex{4}\):

Знайдіть найбільший спільний коефіцієнт: 22, 11м.

Відповідь

11

У прикладах досі найбільшим загальним фактором була константа. У наступних двох прикладах ми отримаємо змінні в найбільшому загальному факторі.

Приклад\(\PageIndex{3}\):

Знайдіть найбільший загальний коефіцієнт 12x ² та 18x ³.

Рішення

Розподіліть кожен коефіцієнт в прості числа і запишіть змінні з показниками в розгорнутому вигляді. Обведіть загальні фактори в кожному стовпці. Збийте загальні фактори. Помножте коефіцієнти.

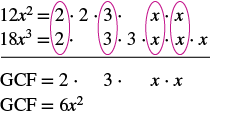GCF 12x ² і 18x ³ 6x ².

Вправа\(\PageIndex{5}\):

Знайдіть найбільший загальний фактор: 16x ², 24x ³.

Відповідь

\(8x^2\)

Вправа\(\PageIndex{6}\):

Знайдіть найбільший загальний фактор: 27y ³, 18y ⁴.

Відповідь

\(9y^3\)

Приклад\(\PageIndex{4}\):

Знайдіть найбільший загальний коефіцієнт 14x ³, 8x ², 10x.

Рішення

Розподіліть кожен коефіцієнт в прості числа і запишіть змінні з показниками в розгорнутому вигляді. Обведіть загальні фактори в кожному стовпці. Збийте загальні фактори. Помножте коефіцієнти.

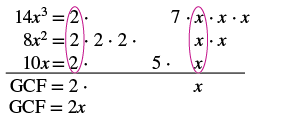GCF 14x ³ і 8x ², а 10x - 2x.

Вправа\(\PageIndex{7}\):

Знайдіть найбільший загальний фактор: 21x ³, 9x ², 15x.

Відповідь

3х

Вправа\(\PageIndex{8}\):

Знайдіть найбільший загальний фактор: 25m ⁴, 35m ³, 20m ².

Відповідь

\(5m^2\)

Фактор найбільший спільний фактор з полінома

Так само, як і в арифметиці, де іноді корисно представляти число у факторованій формі (наприклад, 12 як 2 • 6 або 3 • 4), в алгебрі може бути корисно представляти многочлен у факторованій формі. Один із способів зробити це - знайти найбільший загальний фактор усіх термінів. Пам'ятайте, що множити многочлен на моном можна наступним чином:

\[\begin{split} 2(x &+ 7) \quad factors \\ 2 \cdot x &+ 2 \cdot 7 \\ 2x &+ 14 \quad product \end{split}\]

Тут ми почнемо з продукту, як 2x + 14, і закінчимо його факторами, 2 (x + 7). Для цього застосовуємо розподільну властивість «в зворотному напрямку».

Визначення: Розподільна власність

Якщо a, b, c - дійсні числа, то a (b + c) = ab + ac і ab + ac = a (b + c).

Форма зліва використовується для множення. Форма праворуч використовується для фактора.

Отже, як ми використовуємо розподільну властивість для множника полінома? Знаходимо GCF всіх термінів і пишемо многочлен як добуток!

Приклад\(\PageIndex{5}\):

Коефіцієнт: 2х+ 14.

Рішення

Крок 1: Знайдіть GCF всіх членів многочлена.	Знайдіть GCF 2х і 14.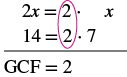
Крок 2: Перепишіть кожен термін як продукт за допомогою GCF.	Перепишіть 2х і 14 як продукти своїх GCF, 2. $\ почати {спліт} 2x &= 2\ cdot x\\ 14 &= 2\ cdot 7\ кінець {спліт} $$	$\ begin {спліт} 2x &+ 14\\ textcolor {червоний} {2}\ крапка х &+\ колір тексту {червоний} {2}\ cdot 7\ кінець {спліт} $$
Крок 3: Використовуйте розподільну властивість «навпаки» для фактора виразу.		2 (х + 7)
Крок 4: Перевірте, множивши коефіцієнти.	Перевірте.	$\ begin {спліт} 2 (x &+ 7)\\ 2\ cdot x &+ 2\ cdot 7\\ 2x &+ 14\;\ галочка\ кінець {спліт} $$

Вправа\(\PageIndex{9}\):

Коефіцієнт: 4х+ 12.

Відповідь

4 (х + 3)

Вправа\(\PageIndex{10}\):

Фактор: 6а+ 24.

Відповідь

6 (а + 4)

Зверніть увагу, що в прикладі 10.84 ми використовували слово фактор як іменник і дієслово:

Іменник	7 - коефіцієнт 14
дієслово	Фактор 2 від 2х + 14

ЯК: ФАКТОР НАЙБІЛЬШОГО ЗАГАЛЬНОГО ФАКТОРА З ПОЛІНОМА

Крок 1. Знайдіть ЗКФ всіх членів многочлена.

Крок 2. Перепишіть кожен термін як продукт за допомогою GCF.

Крок 3. Використовуйте розподільну властивість «у зворотному напрямку» для фактора виразу.

Крок 4. Перевірте, множивши коефіцієнти.

Приклад\(\PageIndex{6}\):

Фактор: 3а+ 3.

Рішення

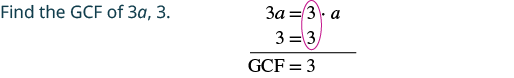Перепишіть кожен термін як продукт за допомогою GCF.	$\ колір тексту {червоний} {3}\ крапка а +\ колір тексту {червоний} {3}\ крапка 1$$
Використовуйте розподільну властивість «у зворотному напрямку», щоб врахувати GCF.	$3 (а+1) $$
Перевірте, множивши коефіцієнти, щоб отримати вихідний многочлен.	$\ begin {спліт} 3 (a &+ 1)\\ 3\ cdot a &= 3\ cdot 1\\ 3a &+ 3\;\ галочка\ кінець {спліт} $$

Вправа\(\PageIndex{11}\):

Фактор: 9а+ 9.

Відповідь

9 (а + 1)

Вправа\(\PageIndex{12}\):

Коефіцієнт: 11х+ 11.

Відповідь

11 (х + 1)

Вирази в наступному прикладі мають кілька спільних факторів. Не забудьте написати GCF як добуток всіх загальних факторів.

Приклад\(\PageIndex{7}\):

Коефіцієнт: 12x − 60.

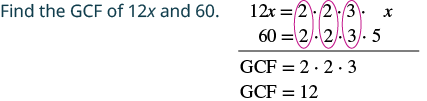Перепишіть кожен термін як продукт за допомогою GCF.	$\ колір тексту {червоний} {12}\ крапка х -\ колір тексту {червоний} {12}\ крапка 5$$
Фактор GCF.	$12 (х-5) $$
Перевірте, множивши коефіцієнти.	$\ почати {спліт} 12 (x &- 5)\\ 12\ cdot x &- 12\ cdot 5\\ 12x &- 60\;\ галочка\ кінець {спліт} $$

Вправа\(\PageIndex{13}\):

Коефіцієнт: 11x − 44.

Відповідь

11 (х - 4)

Вправа\(\PageIndex{14}\):

Коефіцієнт: 13% − 52.

Відповідь

13 (у - 4)

Тепер ми будемо враховувати найбільший загальний фактор з триноміалу. Почнемо з пошуку GCF всіх трьох термінів.

Приклад\(\PageIndex{8}\):

Коефіцієнт: 3й ² + 6й + 9.

Рішення

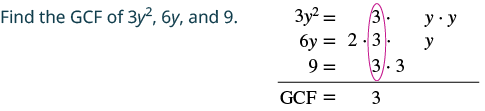Перепишіть кожен термін як продукт за допомогою GCF.	$\ колір тексту {червоний} {3}\ крапка y^ {2} +\ колір тексту {червоний} {3}\ крапка 2y +\ колір тексту {червоний} {3}\ точка 3$
Фактор GCF.	$3 (у ^ {2} + 2р+ 3) $$
Перевірка шляхом множення.	$\ почати {спліт} 3 (y^ {2} &+ 2y+ 3)\\ 3\ cdot y^ {2} &+ 3\ cdot 2y + 3\ cdot 3\ cdot 3\\ 3y^ {2} &+ 6y + 9\;\ галочка\ кінець {спліт} $$

Вправа\(\PageIndex{15}\):

Коефіцієнт: 4й ² + 8р + 12.

Відповідь

\(4\left(y^{2}+2 y+3\right) \)

Вправа\(\PageIndex{16}\):

Коефіцієнт: 6х ² + 42х − 12.

Відповідь

\( 6\left(x^{2}+7 x-2\right) \)

У наступному прикладі ми множимо змінну з біноміального.

Приклад\(\PageIndex{9}\):

Коефіцієнт: 6х ² + 5х.

Рішення

Знайдіть GCF 6x ^2 та 5x та математику, яка йде з ним.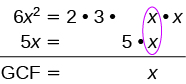
Перепишіть кожен термін як продукт.	$\ колір тексту {червоний} {x}\ крапка 6x +\ колір тексту {червоний} {x}\ cdot 5$$
Фактор GCF.	$х (6х + 5) $$
Перевірка шляхом множення.	$\ почати {спліт} x (6x &+ 5)\\ x\ cdot 6x &+ x\ cdot 5\\ 6x^ {2} &+ 5x\;\ галочка\ кінець {спліт} $$

Вправа\(\PageIndex{17}\):

Коефіцієнт: 9х ² + 7х.

Відповідь

\( x(9x+7) \)

Вправа\(\PageIndex{18}\):

Коефіцієнт: 5а ² − 12а.

Відповідь

а (5а - 12)

Коли є кілька загальних факторів, як ми побачимо в наступних двох прикладах, хороша організація і акуратна робота допомагає!

Приклад\(\PageIndex{10}\):

Коефіцієнт: 4х ³ − 20х ².

Рішення

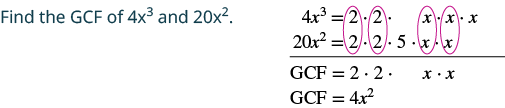Перепишіть кожен термін.	$\ колір тексту {червоний} {4x^ {2}}\ крапка х -\ колір тексту {червоний} {4x^ {2}}\ cdot 5$$
Фактор GCF.	$4х^ {2} (х-5) $$
Перевірте.	$\ почати {спліт} 4x^ {2} (x &- 5)\\ 4x^ {2}\ cdot x &- 4x^ {2}\ cdot 5\\ 4x^ {3} &- 20x^ {2}\;\ галочка\ кінець {спліт} $$

Вправа\(\PageIndex{19}\):

Фактор: 2х ³ + 12х ².

Відповідь

\( 2 x^{2}(x+6) \)

Вправа\(\PageIndex{20}\):

Коефіцієнт: 6й ³ − 15й ².

Відповідь

\( 3 y^{2}(2 y-5) \)

Приклад\(\PageIndex{11}\):

Фактор: 21р ² + 35р.

Рішення

Знайти GCF 21y ^2 і 35y.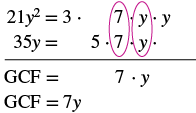
Перепишіть кожен термін.	$\ колір тексту {червоний} {7y}\ крапка 3y +\ колір тексту {червоний} {7y}\ точка 5$$
Фактор GCF.	$7 за рік (3 роки + 5) $$

Вправа\(\PageIndex{21}\):

Фактор: 18р ² + 63р.

Відповідь

9 років (2 + 7)

Вправа\(\PageIndex{22}\):

Фактор: 32к ² + 56к.

Відповідь

8к (4к + 7)

Приклад\(\PageIndex{12}\):

Коефіцієнт: 14х ³ + 8х ² − 10х.

Рішення

Раніше ми виявили, що GCF 14x ³, 8x ² та 10x буде 2x.

Перепишіть кожен термін за допомогою GCF, 2x.	$\ колір тексту {червоний} {2x}\ крапка 7x^ {2} +\ колір тексту {червоний} {2x}\ крапка 4x -\ колір тексту {червоний} {2x}\ cdot 5$
Фактор GCF.	$2х (7х^ {2} + 4х - 5) $$
Перевірте.	$\ почати {спліт} 2x (7x^ {2} &+ 4x - 5)\\ 2x\ cdot 7x^ {2} &+ 2x\ cdot 4x - 2x\ cdot 5\\ 14x^ {3} &+ 8x^ {2} - 10x\;\ галочка\ кінець {спліт} $

Вправа\(\PageIndex{23}\):

Коефіцієнт: 18й ³ − 6й ² − 24р.

Відповідь

\(6 y\left(3 y^{2}-y-4\right)\)

Вправа\(\PageIndex{24}\):

Коефіцієнт: 16х ³ + 8х ² − 12х.

Відповідь

\(4 x\left(4 x^{2}+2 x-3\right)\)

Коли провідний коефіцієнт, коефіцієнт першого члена, негативний, ми перераховуємо негатив у складі GCF.

Приклад\(\PageIndex{13}\):

Коефіцієнт: −9y − 27.

Рішення

Коли провідний коефіцієнт негативний, ГКФ буде негативним. Ігноруючи ознаки термінів, ми спочатку знаходимо GCF 9y і 27 дорівнює 9.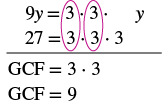
Оскільки вираз −9y − 27 має від'ємний провідний коефіцієнт, ми використовуємо −9 як GCF.
Перепишіть кожен термін за допомогою GCF.	$\ колір тексту {червоний} {-9}\ точка y + (\ колір тексту {червоний} {-9})\ точка 3$$
Фактор GCF.	$-9 (у+3) $$
Перевірте.	$\ begin {спліт} -9 (y &+ 3)\\ -9\ cdot y &+ (-9)\ cdot 3\\ -9y &- 27\;\ галочка\ кінець {спліт} $$

Вправа\(\PageIndex{25}\):

Коефіцієнт: −5y − 35.

Відповідь

-5 (у + 7)

Вправа\(\PageIndex{26}\):

Коефіцієнт: −16z − 56.

Відповідь

-8 (2з + 7)

Зверніть пильну увагу на ознаки термінів в наступному прикладі.

Приклад\(\PageIndex{14}\):

Коефіцієнт: −4a ² + 16a.

Рішення

Провідний коефіцієнт негативний, тому ГКФ буде негативним.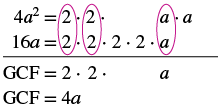
Оскільки провідний коефіцієнт від'ємний, GCF є від'ємним, −4a.
Перепишіть кожен термін.	$\ колір тексту {червоний} {-4a}\ крапка a - (\ колір тексту {червоний} {-4a})\ точка 4$$
Фактор GCF.	$$-4а (а-4) $$
Перевірте на свій розсуд шляхом множення.

Вправа\(\PageIndex{27}\):

Коефіцієнт: −7а ² + 21а.

Відповідь

-7а (а - 3)

Вправа\(\PageIndex{28}\):

Коефіцієнт: −6x ² + x.

Відповідь

-х (6х - 1)

ДОСТУП ДО ДОДАТКОВИХ ОНЛАЙН-РЕСУРСІВ

Фактор GCF

Біноміальний фактор

Визначте GCF

Практика робить досконалим

Знайдіть найбільший спільний фактор двох або більше виразів

У наступних вправах знайдіть найбільший загальний фактор.

422. 40, 56
423. 45, 75
424. 72, 162
425. 150, 275
426. 3х, 12
427. 4-й, 28
428. 10а, 50
429. 5б, 30
430. 16 р., 24 р. ²
431. 9х, ^15х2
432. 18м ³, 36м ²
433. 12п ⁴, 48п ³
434. 10х, 25х ², 15х ³
435. 18а, 6а ², 22а ³
436. 24у, 6у ², 30у ³
437. 40г, 10 р ², 90р ³
438. 15а ⁴, 9а ⁵, 21а ⁶
439. 35х ³, 10х ⁴, 5х ⁵
440. 27 р ², 45 р ³, 9 р ⁴
441. 14б ², 35б ³, 63б ⁴

Фактор найбільший спільний фактор з полінома

У наступних вправах фактор найбільший загальний фактор з кожного полінома.

442. 2х + 8
443. 5 років + 15
444. 3а − 24
445. 4б − 20
446. 9 років − 9
447. 7x − 7
448. 5м ² + 20м + 35
449. 3н ² + 21н + 12
450. 8р ² +32п + 48
451. 6 кв. ² + 30 кв + 42
452. 8 кв ² + 15кв
453. 9с ² +22с
454. 13к ² + 5к
455. 17х ² + 7х
456. 5с ² + 9с
457. 4кв ² + 7кв
458. 5п ² +25р
459. 3р ² + 27р
460. 24 квартал ² − 12кв
461. 30u ² − 10 годин
462. Яз + 4Гц
463. аб + 8б
464. 60х − 6х ³
465. 55 років − 11 років ⁴
466. 48р ⁴ − 12 р. ³
467. 45c ³ − 15c ²
468. 4а ³ − 4аб ²
469. 6с ³ − 6кд ²
470. 30у ³ + 80у ²
471. 48х ³ + 72х ²
472. 120г ⁶ + 48 років ⁴
473. 144а ⁶ + 90а ³
474. 4 кв ² + 24 кв + 28
475. 10 років ² + 50 років + 40
476. 15з ² − 30z − 90
477. 12 - ² − 36у − 108
478. 3а ⁴ − 24а ³ + 18а ²
479. 5 п. ⁴ − 20п ³ − 15п ²
480. 11х ⁶ + 44х ⁵ − 121х ⁴
481. 8c ⁵ + 40c ⁴ − 56c ³
482. −3n − 24
483. −7p − 84
484. −15а − ² − 40а
485. −18b ² − 66б
486. −10 років ³ + 60 років ²
487. −8а ³ + 32а ²
488. −4у ⁵ +56у ³
489. −9б ⁵ + 63б ³

Щоденна математика

490. Виручка Виробник мікрохвильових печей виявив, що дохід, отриманий від продажу мікрохвильових печей, вартість р доларів кожна дається поліномом −5p ² + 150p. Фактор найбільший загальний фактор від цього многочлена.
491. Висота бейсболу Висота бейсбольного удару зі швидкістю 80 футів/секунду на 4 футах над рівнем землі становить −16t ² + 80t + 4, з t = кількість секунд з моменту удару. Фактор найбільший загальний фактор від цього многочлена.

Письмові вправи

492. Найбільший загальний коефіцієнт 36 і 60 - 12. Поясніть, що це означає.
493. Що таке GCF у ⁴, у ⁵, і у ¹⁰? Напишіть загальне правило, яке підказує, як знайти GCF y ^a, y ^b і y ^c.

Самостійна перевірка

(а) Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

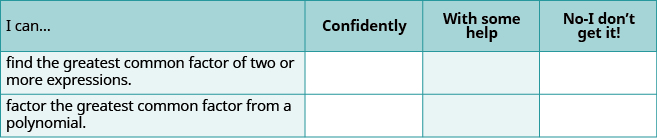
(b) Загалом, подивившись контрольний список, ви вважаєте, що добре підготовлені до наступної глави? Чому чи чому ні?

Дописувачі та атрибуція

• Template:ContribOpenStaxPreAlgebra