Skip to main content
LibreTexts - Ukrayinska

10.5: Множення многочленів (частина 2)

  1. Last updated
  2. Save as PDF
  • Page ID
    57888

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Використання методу FOIL

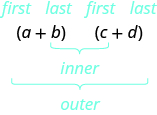
    Пам'ятайте, що коли ви множите біном на біном, ви отримуєте чотири члени. Іноді ви можете комбінувати подібні терміни, щоб отримати триноміал, але іноді немає подібних термінів для поєднання. Давайте ще раз розглянемо останній приклад і звернемо особливу увагу на те, як ми отримали чотири терміни.

    \[\begin{split} (x + 2)&(x - y) \\ x^{2} - xy &+ 2x - 2y \end{split}\]

    Звідки взявся перший термін, x 2?

    Це добуток x та x, перших членів у (x + 2) та (x − y).

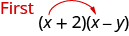
    Буде показано дужки x плюс 2 рази дужки x мінус y. Існує червона стрілка від першого х до другого. Крім цього, червоним кольором написано «Перший».

    Наступний термін, −xy, є добутком x та − y, двох зовнішніх членів.

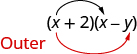
    Буде показано дужки x плюс 2 рази дужки x мінус y. Існує чорна стрілка від першої x до другої x. Є червона стрілка від першої x до y. Крім цього, червоним кольором написано «Зовнішній».

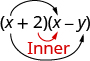
    Третій член, +2x, є добутком 2 і х, двох внутрішніх членів.

    Буде показано дужки x плюс 2 рази дужки x мінус y. Існує чорна стрілка від першої x до другої x. Є чорна стрілка від першої x до y. Тут є червона стрілка від 2 до x. Під нею червоним кольором написано «Inner».

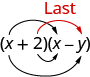
    І останній термін, −2y, походить від множення двох останніх термінів.

    Буде показано дужки x плюс 2 рази дужки x мінус y. Існує чорна стрілка від першої x до другої x. Є чорна стрілка від першої x до y. Є чорна стрілка від 2 до x. Є червона стрілка від 2 до y. Над нею написано «Останній» червоним кольором.

    Ми скорочуємо «Перший, Зовнішній, Внутрішній, Останній» як FOIL. Букви позначають «Перший, Зовнішній, Внутрішній, Останній». Слово FOIL легко запам'ятати і гарантує, що ми знаходимо всі чотири продукти. Можна сказати, що ми використовуємо метод FOIL для множення двох біноміалів.

    Буде показано дужки a плюс b кратні дужки c плюс d. Вище a перший, вище b останній, вище c - перший, вище d - останній. Існує дужка, що з'єднує a і d, що говорить зовнішній. Існує дужка, що з'єднує b і c, яка говорить внутрішня.

    Давайте подивимося на (х + 3) (х + 7) ще раз. Тепер ми попрацюємо над прикладом, де ми використовуємо шаблон FOIL для множення двох біноміалів.

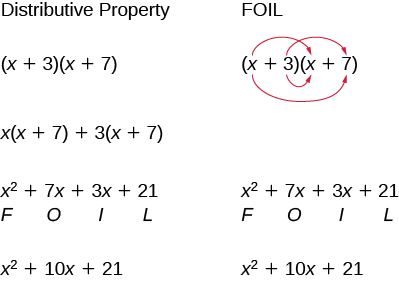
    CNX_BMath_Figure_10_03_063_img.jpg

    Приклад\(\PageIndex{11}\):

    Множення за допомогою методу FOIL: (x + 6) (x + 9).

    Рішення

    Крок 1: Помножте Перші члени. 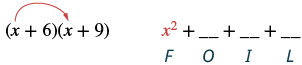CNX_BMath_Figure_10_03_054_img-01.png
    Крок 2: Помножте Зовнішні члени. 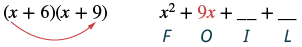CNX_BMath_Figure_10_03_054_img-02.png
    Крок 3: Помножте Внутрішні члени. 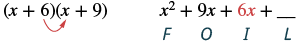CNX_BMath_Figure_10_03_054_img-03.png
    Крок 4: Множимо Останні члени. 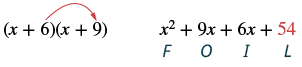CNX_BMath_Figure_10_03_054_img-04.png
    Крок 5: Комбінуйте подібні терміни, коли це можливо. х 2 + 15х+54
    Вправа\(\PageIndex{21}\):

    Множення за допомогою методу FOIL: (x + 7) (x + 8).

    Відповідь

    \(x^2+15x+56 \)

    Вправа\(\PageIndex{22}\):

    Множення за допомогою методу FOIL: (y + 14) (y + 2).

    Відповідь

    \(y^2+16y+28\)

    Нижче ми підсумуємо кроки методу FOIL. Метод FOIL застосовується лише до множення бічленів, а не інших поліномів!

    ЯК: ВИКОРИСТОВУЙТЕ МЕТОД ФОЛЬГИ ДЛЯ МНОЖЕННЯ ДВОХ БІНОМІАЛІВ

    Крок 1. Помножте Перші члени.

    Крок 2. Помножте Зовнішні члени.

    Крок 3. Помножте Внутрішні члени.

    Крок 4. Помножте Останні члени.

    Крок 5. Поєднуйте подібні терміни, коли це можливо.

    Буде показано дужки a плюс b кратні дужки c плюс d. Вище a перший, вище b останній, вище c - перший, вище d - останній. Існує дужка, що з'єднує a і d, що говорить зовнішній. Існує дужка, що з'єднує b і c, яка говорить внутрішня.

    Приклад\(\PageIndex{12}\):

    Помножте: (y − 8) (y + 6).

    Рішення

    Крок 1: Помножте Перші члени. 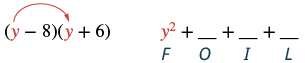CNX_BMath_Figure_10_03_055_img-01.png
    Крок 2: Помножте Зовнішні члени. 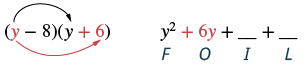CNX_BMath_Figure_10_03_055_img-02.png
    Крок 3: Помножте Внутрішні члени. 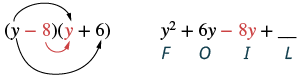CNX_BMath_Figure_10_03_055_img-03.png
    Крок 4: Множимо Останні члени. 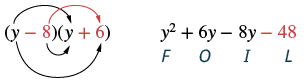CNX_BMath_Figure_10_03_055_img-04.png
    Крок 5: Комбінуйте подібні терміни, коли це можливо. у 2 - 2й - 48
    Вправа\(\PageIndex{23}\):

    Помножте: (y − 3) (y + 8).

    Відповідь

    \(y^2+5y-24 \)

    Вправа\(\PageIndex{24}\):

    Помножте: (q − 4) (q + 5).

    Відповідь

    \(q^2+q-20 \)

    Приклад\(\PageIndex{13}\):

    Множимо: (2а + 3) (3a − 1).

    Рішення

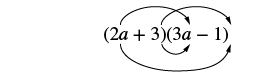      CNX_BMath_Figure_10_03_056_img-02.png
    Помножте Перші члени. 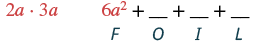CNX_BMath_Figure_10_03_056_img-03.png
    Помножте Зовнішні члени. 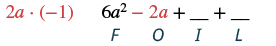CNX_BMath_Figure_10_03_056_img-04.png
    Помножте Внутрішні члени. 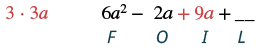CNX_BMath_Figure_10_03_056_img-05.png
    Помножте Останні члени. 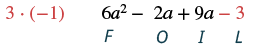CNX_BMath_Figure_10_03_056_img-06.png
    Поєднуйте подібні терміни. 6а 2 + 7а - 3
    Вправа\(\PageIndex{25}\):

    Множимо: (4a + 9) (5a − 2).

    Відповідь

    \(20a^2+37a-18 \)

    Вправа\(\PageIndex{26}\):

    Помножте: (7x + 4) (7x − 8).

    Відповідь

    \( 49x^2-28x-32\)

    Приклад\(\PageIndex{14}\):

    Помножте: (5x − y) (2x − 7).

    Рішення

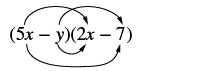      CNX_BMath_Figure_10_03_057_img-02.png
    Помножте Перші члени. 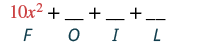CNX_BMath_Figure_10_03_057_img-03.png
    Помножте Зовнішні члени. 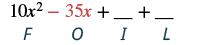CNX_BMath_Figure_10_03_057_img-04.png
    Помножте Внутрішні члени. 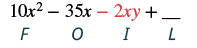CNX_BMath_Figure_10_03_057_img-05.png
    Помножте Останні члени. 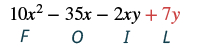CNX_BMath_Figure_10_03_057_img-06.png
    Поєднуйте подібні терміни. Їх немає. 10х 2 - 35х - 2х + 7г
    Вправа\(\PageIndex{27}\):

    Помножте: (12x − y) (x − 5).

    Відповідь

    \(12 x^{2}-60 x-x y+5 y \)

    Вправа\(\PageIndex{28}\):

    Помножте: (6a − b) (2a − 9).

    Відповідь

    \(12 a^{2}-54 a-2 a b+9 b \)

    Використання вертикального методу

    Метод FOIL, як правило, є найшвидшим методом множення двох біноміалів, але він працює лише для біноміалів. Ви можете використовувати розподільну властивість, щоб знайти добуток будь-яких двох поліномів. Ще один метод, який працює для всіх поліномів, - це Вертикальний метод. Це дуже схоже на метод, який ви використовуєте для множення цілих чисел. Подивіться уважно на цей приклад множення двозначних чисел.

    Показано вертикальну задачу множення. 23 рази 46 написано з рядком під ним. Під лінією 138. Поряд з 138 написано «частковий твір». Під 138 - 92. Поряд з 92 написано «частковий твір». Під 92 знаходиться лінія і 1058. Поряд з 1058 написано «продукт».

    Ви починаєте з множення 23 на 6, щоб отримати 138. Потім ви множите 23 на 4, вибудовуючи часткове виріб в правильні стовпці. Останній, ви додаєте часткові продукти. Тепер ми застосуємо цей же метод, щоб помножити два біноміали.

    Приклад\(\PageIndex{15}\):

    Множення за допомогою вертикального методу: (5x − 1) (2x − 7).

    Рішення

    Неважливо, який біноміал йде на верхівці. Вибудовуйте стовпці, коли ви множите, як ми робили, коли ми помножили 23 (46).

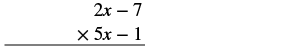      CNX_BMath_Figure_10_03_059_img-01.png
    Помножте 2x − 7 на −1. CNX_BMath_Figure_10_03_059_img-02.png
    Помножте 2x − 7 на 5x. CNX_BMath_Figure_10_03_059_img-03.png
    Додайте подібні терміни. 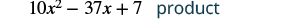CNX_BMath_Figure_10_03_059_img-04.png

    Зверніть увагу, що часткові продукти такі ж, як терміни в методі FOIL.

    Зліва показано 5х мінус 1 раз 2х мінус 7. Нижче це 10 х квадрат мінус 35x мінус 2x плюс 7. Перші два члени синім кольором, другі два червоним кольором. Під цим 10 х квадрат мінус 37x плюс 7. Праворуч показано вертикальну задачу множення. 2xx мінус 7 разів 5x мінус 1 записується з рядком під ним. Під лінією знаходиться червоний мінус 2x плюс 7. Під цим 10 х квадрат мінус 35 х синім кольором. Під цим є ще один рядок. Під цією лінією 10 х квадрат мінус 37x плюс 7.

    Вправа\(\PageIndex{29}\):

    Множення вертикальним методом: (4m − 9) (3m − 7).

    Відповідь

    \( 12 m^{2}-55 m+63\)

    Вправа\(\PageIndex{30}\):

    Множення вертикальним методом: (6n − 5) (7n − 2).

    Відповідь

    \(42 n^{2}-47 n+10 \)

    Зараз ми використали три методи множення біноміалів. Обов'язково практикуйте кожен метод, і спробуйте вирішити, який з них ви віддаєте перевагу. Три методи перераховані тут, щоб допомогти вам їх запам'ятати.

    Визначення: Множення двох біноміалів

    Щоб помножити біноміали, використовуйте:

    • Розподільна власність
    • Фольга метод
    • вертикальний метод

    Пам'ятайте, що FOIL працює лише при множенні двох біноміалів.

    Помножте триноміал на біноміал

    Ми помножили мономи на мономи, мономи на многочлени та біноми на біноми. Тепер ми готові помножити тріноміал на біноміал. Пам'ятайте, що метод FOIL в цьому випадку не спрацює, але ми можемо використовувати або властивість Distributive, або вертикальний метод. Спочатку ми розглянемо приклад з використанням розподільного властивості.

    Приклад\(\PageIndex{16}\):

    Множення за допомогою розподільної властивості: (x + 3) (2x 2 − 5x + 8).

    Рішення

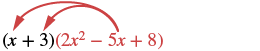      CNX_BMath_Figure_10_03_061_img-01.png
    Розподілити. CNX_BMath_Figure_10_03_061_img-02.png
    Помножити. 2х 3 − 5х 2 + 8х + 6х 2 − 15х + 24
    Поєднуйте подібні терміни. 2х 3+ х 2 − 7х + 24
    Вправа\(\PageIndex{31}\):

    Множення за допомогою розподільної властивості: (y − 1) (y 2 − 7y + 2).

    Відповідь

    \( y^{3}-8 y^{2}+9 y-2\)

    Вправа\(\PageIndex{32}\):

    Множення за допомогою розподільної властивості: (x + 2) (3x 2 − 4x + 5).

    Відповідь

    \( 3 x^{3}+2 x^{2}-3 x+10\)

    Тепер давайте зробимо це ж множення за допомогою вертикального методу.

    Приклад\(\PageIndex{17}\):

    Множення за допомогою вертикального методу: (x + 3) (2x 2 − 5x + 8).

    Рішення

    Простіше поставити многочлен з меншою кількістю членів на дно, оскільки таким чином ми отримуємо менше часткових продуктів.

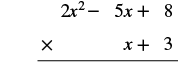      CNX_BMath_Figure_10_03_062_img-01.png
    Помножте (2x 2 − 5x + 8) на 3. 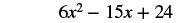CNX_BMath_Figure_10_03_062_img-02.png
    Помножте (2x 2 − 5x + 8) на x. 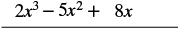CNX_BMath_Figure_10_03_062_img-03.png
    Додайте подібні терміни. 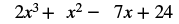CNX_BMath_Figure_10_03_062_img-04.png
    Вправа\(\PageIndex{33}\):

    Множення за допомогою вертикального методу: (y − 1) (y 2 − 7y + 2).

    Відповідь

    \(y^{3}-8 y^{2}+9 y-2 \)

    Вправа\(\PageIndex{34}\):

    Множення за допомогою вертикального методу: (x + 2) (3x 2 − 4x + 5).

    Відповідь

    \( 3 x^{3}+2 x^{2}-3 x+10\)

    ДОСТУП ДО ДОДАТКОВИХ ОНЛАЙН-РЕСУРСІВ

    Множення мономіалів

    Множення многочленів

    Множення многочленів 2

    Огляд множення поліномів

    Множення многочленів за допомогою розподільної властивості

    Помножити Біноміали

    Практика робить досконалим

    Помножити многочлен на мономіал

    У наступних вправах помножте.

    1. 4 (х + 10)
    2. 6 (у + 8)
    3. 15 (r − 24)
    4. 12 (в− 30)
    5. −3 (м + 11)
    6. −4 (р + 15)
    7. −8 (з − 5)
    8. −3 (x − 9)
    9. (до +5)
    10. q (q + 7)
    11. n (n 2 − 3n)
    12. s (s 2 − 6 с)
    13. 12х (х − 10)
    14. 9м (м − 11)
    15. −9а (3а + 5)
    16. −4р (2п + 7)
    17. 6х (4х + у)
    18. 5а (9а + б)
    19. 5 р. (11п − 5кв)
    20. 12u (3u − 4 в)
    21. 3 (в 2 + 10в + 25)
    22. 6 (х 2 + 8х + 16)
    23. 2n (4n 2 − 4n + 1)
    24. 3 (2р 2 − 6р + 2)
    25. −8г (у 2 + 2й − 15)
    26. −5м (м 2+ 3м − 18)
    27. 5кв 3 (q 2 − 2кв + 6)
    28. 9 р 3 (р 2 − 3р + 5)
    29. −4з 2 (3з 2 + 12з − 1)
    30. −3х 2 (7х 2 + 10х − 1)
    31. (2 — 9 років)
    32. (8b − 1) б
    33. (вт − 6) • 8
    34. (к − 4) • 5

    Помножте біноміал на біноміал

    У наступних вправах помножте наступні біноміали, використовуючи: (а) розподільну властивість (b) метод FOIL (c) метод Вертикальний

    1. (х + 4) (х + 6)
    2. (до + 8) (до + 2)
    3. (n + 12) (n − 3)
    4. (у + 3) (y − 9)

    У наступних вправах перемножте наступні біноміали. Використовуйте будь-який метод.

    1. (у + 8) (у + 3)
    2. (х + 5) (х + 9)
    3. (а + 6) (а + 16)
    4. (q + 8) (q + 12)
    5. (u − 5) (u − 9)
    6. (r − 6) (r − 2)
    7. (з − 10) (з − 22)
    8. (b − 5) (b − 24)
    9. (x − 4) (x + 7)
    10. (с − 3) (и + 8)
    11. (v + 12) (v − 5)
    12. (d + 15) (d − 4)
    13. (6н + 5) (n + 1)
    14. (7й + 1) (у + 3)
    15. (2м − 9) (10м + 1)
    16. (5р − 4) (12р + 1)
    17. (4с − 1) (4с + 1)
    18. (8n − 1) (8n + 1)
    19. (3u − 8) (5u − 14)
    20. (2кв − 5) (7q − 11)
    21. (а + б) (2а + 3б)
    22. (р + с) (3р + 2с)
    23. (5x − у) (x − 4)
    24. (4z − y) (з − 6)

    Помножте триноміал на біноміал

    У наступних вправах помножте, використовуючи (а) розподільну властивість та (b) вертикальний метод.

    1. (у + 4) (у 2 + 3у + 2)
    2. (х + 5) (х 2 + 8х+ 3)
    3. (а + 10) (3а 2 + а − 5)
    4. (n + 8) (4n 2 + n − 7)

    У наступних вправах помножте. Використовуйте будь-який метод.

    1. (y − 6) (y 2 − 10 років + 9)
    2. (k − 3) (k 2 − 8к+ 7)
    3. (2х+ 1) (х 2 − 5х − 6)
    4. (5v + 1) (v 2 − 6v − 10)

    Щоденна математика

    1. Психічна математика Ви можете використовувати біноміальне множення для множення чисел без калькулятора. Скажімо, потрібно помножити 13 разів 15. Подумайте про 13 як 10 + 3 і 15 як 10 + 5.
      1. Помножте (10 + 3) (10 + 5) методом FOIL.
      2. Помножте 13 • 15 без використання калькулятора.
      3. Який шлях вам легше? Чому?
    2. Психічна математика Ви можете використовувати біноміальне множення для множення чисел без калькулятора. Скажімо, потрібно помножити 18 разів 17. Подумайте про 18 як 20 − 2, а 17 як 20 − 3.
      1. Помножте (20 − 2) (20 − 3) методом FOIL.
      2. Помножте 18 • 17 без використання калькулятора.
      3. Який шлях вам легше? Чому?

    Письмові вправи

    1. Який метод ви віддаєте перевагу використовувати при множенні двох біномів - розподільна властивість, метод FOIL або вертикальний метод? Чому?
    2. Який метод ви віддаєте перевагу використовувати при множенні триноміала на біноміал - розподільну властивість або вертикальний метод? Чому?

    Самостійна перевірка

    (а) Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

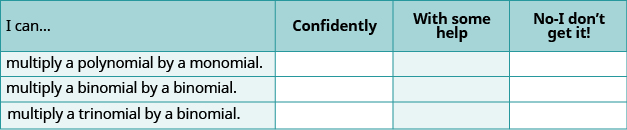
    CNX_BMath_Figure_AppB_061.jpg

    (б) Що цей контрольний список розповідає вам про ваше володіння цим розділом? Які кроки ви зробите для вдосконалення?

    Автори та атрибуція