Skip to main content
LibreTexts - Ukrayinska

5.10: Співвідношення та ставка (частина 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    57897

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • Напишіть співвідношення як дріб
    • Запишіть швидкість у вигляді дробу
    • Знайти одиничні ставки
    • Знайти ціну за одиницю
    • Перекладіть фрази на вирази з дробами
    будьте готові!

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Спростити:\(\dfrac{16}{24}\). Якщо ви пропустили цю проблему, перегляньте приклад 4.3.1.
    2. Розділити: 2,76 ÷ 11,5. Якщо ви пропустили цю проблему, перегляньте приклад 5.4.9.
    3. Спростити:\(\dfrac{1 \dfrac{1}{2}}{2 \dfrac{3}{4}}\). Якщо ви пропустили цю проблему, перегляньте приклад 4.5.7.

    Напишіть коефіцієнт як дріб

    Коли ви подаєте заявку на іпотеку, кредитний співробітник буде порівнювати загальну заборгованість із загальним доходом, щоб вирішити, чи маєте ви право на кредит. Таке порівняння називається співвідношенням заборгованості до доходу. Співвідношення порівнює дві величини, які вимірюються з однаковою одиницею. Якщо порівнювати a і b, співвідношення записується як a до b\(\dfrac{a}{b}\), або a:b.

    Визначення: коефіцієнти

    Співвідношення порівнює два числа або дві величини, які вимірюються з однаковою одиницею. Співвідношення a до b записується a до b\(\dfrac{a}{b}\), або a:b.

    У цьому розділі ми будемо використовувати позначення дробу. Коли співвідношення записується у вигляді дробу, дріб слід спростити. Якщо це неправильний дріб, ми не змінюємо його на змішане число. Оскільки співвідношення порівнює дві величини, ми залишили б співвідношення\(\dfrac{4}{1}\) замість спрощення його до 4, щоб ми могли бачити дві частини співвідношення.

    Приклад\(\PageIndex{1}\):

    Запишіть кожне співвідношення як дріб: (а) 15 до 27 (б) 45 до 18.

    Рішення

    (а) від 15 до 27

    Запишіть як дріб з першим числом в чисельнику і другим в знаменнику. $$\ фрак {15} {27} $$
    Спростити дріб. $$\ фрак {5} {9} $$

    (б) від 45 до 18

    Запишіть як дріб з першим числом в чисельнику і другим в знаменнику. $$\ фрак {45} {18} $$
    Спростити. $$\ дфрак {5} {2} $$

    Ми залишаємо співвідношення в (b) як неправильний дріб.

    Вправа\(\PageIndex{1}\):

    Запишіть кожне співвідношення як дріб: (а) 21 до 56 (b) 48 до 32.

    Відповідь на

    \(\dfrac{3}{8}\)

    Відповідь б

    \(\dfrac{3}{2}\)

    Вправа\(\PageIndex{2}\):

    Запишіть кожне співвідношення як дріб: (а) 27 до 72 (b) 51 до 34.

    Відповідь на

    \(\dfrac{1}{1}\)

    Відповідь б

    \(\dfrac{3}{2}\)

    Коефіцієнти за участю десяткових знаків

    Ми часто працюватимемо зі співвідношеннями десяткових знаків, особливо коли у нас є коефіцієнти, пов'язані з грошима. У цих випадках ми можемо усунути десяткові числа, використовуючи властивість еквівалентних дробів для перетворення співвідношення в дріб з цілими числами в чисельнику та знаменнику.

    Для прикладу розглянемо співвідношення 0,8 до 0,05. Ми можемо записати його як дріб з десятковими числами, а потім помножити чисельник і знаменник на 100, щоб усунути десяткові числа.

    \[\dfrac{0.8}{0.05}\]

    \[\dfrac{(0.8) \textcolor{red}{100}}{(0.05) \textcolor{red}{100}}\]

    \[\dfrac{80}{5}\]

    Ви бачите ярлик, щоб знайти еквівалентний дріб? Зверніть увагу, що 0,8 =\(\dfrac{8}{10}\) і 0,05 =\(\dfrac{5}{100}\). Найменш спільний знаменник 5\(\dfrac{8}{10}\) і 100 дорівнює 100. Помноживши чисельник і знаменник\(\dfrac{0.8}{0.05}\) на 100, ми «перемістили» десяткові два розряди вправо, щоб отримати еквівалентний дріб без десяткових знаків. Тепер, коли ми розуміємо математику, що стоїть за процесом, ми можемо знайти дріб без десяткових знаків, як це:

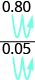
    Верхня лінія говорить 0.80 над 0.05. Є сині стрілки, що переміщають десяткові крапки на 2 місця вправо.

    «Перемістити» десяткові розряди на 2. $$\ фрак {80} {5} $$
    Спростити. $$\ фрак {16} {1} $$

    Вам не доведеться виписувати кожен крок, коли ви множите чисельник і знаменник на ступені десять. Поки ви переміщаєте обидва знака після коми однакову кількість знаків, співвідношення залишатиметься незмінним.

    Приклад\(\PageIndex{2}\):

    Запишіть кожне співвідношення як дріб цілих чисел: (а) 4,8 до 11,2 (b) 2,7 до 0,54

    Рішення

    (а) від 4,8 до 11.2

    Пишіть як дріб. $$\ фрак {4.8} {11.2} $$
    Перепишіть як еквівалентний дріб без десяткових знаків, перемістивши обидві десяткові крапки на 1 місце вправо. $$\ фрак {48} {112} $$
    Спростити. $$\ фрак {3} {7} $$

    Отже, 4.8 до 11.2 еквівалентно\(\dfrac{3}{7}\).

    (б) від 2,7 до 0,54

    Пишіть як дріб. $$\ фрак {2.7} {0.54} $$
    Чисельник має один десятковий знак, а знаменник - 2. Для очищення обох десяткових знаків нам потрібно перемістити десяткові 2 розряди вправо. $$\ фрак {270} {54} $$
    Спростити. $$\ дфрак {5} {1} $$

    Так 2.7 до 0.54 еквівалентно\(\dfrac{5}{1}\).

    Вправа\(\PageIndex{3}\):

    Запишіть кожне співвідношення як дріб: (а) від 4,6 до 11.5 (b) від 2,3 до 0,69.

    Відповідь на

    \(\dfrac{2}{5}\)

    Відповідь б

    \(\dfrac{10}{3}\)

    Вправа\(\PageIndex{4}\):

    Запишіть кожне співвідношення як дріб: (а) від 3,4 до 15,3 (б) від 3,4 до 0,68.

    Відповідь на

    \(\dfrac{2}{9}\)

    Відповідь б

    \(\dfrac{5}{1}\)

    Деякі співвідношення порівнюють два мішаних числа. Пам'ятайте, що для поділу мішаних чисел ви спочатку переписуєте їх як неправильні дроби.

    Приклад\(\PageIndex{3}\):

    Запишіть відношення\(1 \dfrac{1}{4}\) до у\(2 \dfrac{3}{8}\) вигляді дробу.

    Рішення

    Пишіть як дріб. $$\ дфрак {1\ дфрак {1} {4}} {2\ dfrac {3} {8}} $$
    Перетворення чисельника і знаменника в неправильні дроби. $$\ дфрак {\ дфрак {5} {4}} {\ dfrac {19} {8}} $$
    Перепишіть як поділ дробів. $$\ дфрак {5} {4}\ div\ dfrac {19} {8} $$
    Інвертувати дільник і помножити. $\ фрак {5} {4}\ dot\ drac {8} {19} $$
    Спростити. $$\ фрак {10} {19} $$
    Вправа\(\PageIndex{5}\):

    Запишіть кожне співвідношення як дріб:\(1 \dfrac{3}{4}\) до\(2 \dfrac{5}{8}\).

    Відповідь

    \ (\ dfrac {2} {3}\

    Вправа\(\PageIndex{6}\):

    Запишіть кожне співвідношення як дріб:\(1 \dfrac{1}{8}\) до\(2 \dfrac{3}{4}\).

    Відповідь

    \(\dfrac{9}{22}\)

    Застосування коефіцієнтів

    Одне реальне застосування співвідношення, яке впливає на багатьох людей, включає вимірювання холестерину в крові. Співвідношення загального холестерину до холестерину ЛПВЩ - один із способів оцінки лікарями загального стану здоров'я людини. Хорошим вважається співвідношення менше 5 до 1.

    Приклад\(\PageIndex{4}\):

    Загальний холестерин Гектора становить 249 мг/дл, а холестерин ЛПВЩ - 39 мг/дл. (а) Знайти співвідношення його загального холестерину до його холестерину ЛПВЩ. (b) Припускаючи, що співвідношення менше 5 до 1 вважається хорошим, що б ви запропонували Гектору?

    Рішення

    (а) Спочатку напишіть слова, які виражають співвідношення. Ми хочемо знати співвідношення загального холестерину Гектора до його холестерину ЛПВЩ.

    Пишіть як дріб. $\ dfrac {загальний\; холестерин} {ЛПВЩ\; холестерин} $$
    Підставляємо значення. $$\ фрак {249} {39} $$
    Спростити. $$\ фрак {83} {13} $$

    (b) Чи нормально співвідношення холестерину Гектора? Якщо розділити 83 на 13, отримаємо приблизно 6,4, так\(\dfrac{83}{13} \approx \dfrac{6.4}{1}\). Коефіцієнт холестерину Гектора високий! Гектор повинен або знизити загальний рівень холестерину, або підвищити рівень холестерину ЛПВЩ.

    Вправа\(\PageIndex{7}\):

    Знайдіть співвідношення загального холестерину пацієнта до холестерину ЛПВЩ за допомогою наведеної інформації. Загальний холестерин становить 185 мг/дл, а холестерин ЛПВЩ - 40 мг/дл.

    Відповідь

    \ (\ dfrac {37} {8}\

    Вправа\(\PageIndex{8}\):

    Знайдіть співвідношення загального холестерину пацієнта до холестерину ЛПВЩ за допомогою наведеної інформації. Загальний холестерин становить 204 мг/дл, а холестерин ЛПВЩ - 38 мг/дл.

    Відповідь

    \ (\ dfrac {102} {19}\

    Співвідношення двох вимірювань в різних одиницях

    Щоб знайти співвідношення двох вимірювань, ми повинні переконатися, що величини були виміряні однією одиницею. Якщо вимірювання не в однакових одиницях, ми повинні спочатку перетворити їх на однакові одиниці.

    Ми знаємо, що для спрощення дробу ділимо загальні фактори. Аналогічно в співвідношенні вимірювань ділимо загальну одиницю.

    Приклад\(\PageIndex{5}\):

    Правила Закону про американців з обмеженими можливостями (ADA) щодо пандусів для інвалідних крісел вимагають максимального вертикального підйому на 1 дюйм на кожен 1 фут горизонтального ходу. Яке відношення підйому до бігу?

    Рішення

    У співвідношенні виміри повинні бути в однакових одиницях. Ми можемо змінити ноги на дюйми, або дюйми на ноги. Зазвичай простіше перетворити в меншу одиницю, оскільки це дозволяє уникнути введення більшої кількості дробів в проблему. Напишіть слова, які виражають співвідношення.

    Запишіть співвідношення у вигляді дробу. $$\ dfrac {підйом} {запустити} $$
    Підставляємо в задані значення. $$\ dfrac {1\; дюйм} {1\; фут} $$
    Перетворіть 1 фут в дюйми. $\ dfrac {1\; дюйм} {12\; дюймів} $$
    Спростити, розділивши загальні фактори і одиниці. $$\ дфрак {1} {12} $$

    Таким чином, співвідношення підйому до бігу становить 1 до 12. Це означає, що пандус повинен підніматися на 1 дюйм на кожні 12 дюймів горизонтального пробігу, щоб відповідати рекомендаціям.

    Вправа\(\PageIndex{9}\):

    Знайдіть співвідношення першої довжини до другої довжини: 32 дюйма на 1 фут.

    Відповідь

    \ (\ dfrac {8} {3}\

    Вправа\(\PageIndex{10}\):

    Знайдіть співвідношення першої довжини до другої довжини: 1 фут до 54 дюймів.

    Відповідь на

    \ (\ dfrac {2} {9}\

    Запишіть швидкість як дріб

    Часто ми хочемо порівняти два різних типи вимірювань, такі як милі до галонів. Щоб зробити це порівняння, ми використовуємо ставку. Прикладами ставок є 120 миль за 2 години, 160 слів за 4 хвилини та 5 доларів за 64 унції.

    Визначення: ставка

    Ставка порівнює дві величини різних одиниць. Ставка зазвичай записується як дріб.

    При написанні дробу у вигляді ставки ставимо першу задану суму з її одиницями в чисельник і другу суму з її одиницями в знаменник. При спрощенні ставок одиниці залишаються в чисельнику і знаменнику.

    Приклад\(\PageIndex{6}\):

    Боб проїхав свою машину 525 миль за 9 годин. Запишіть цю норму як дріб.

    Рішення

    Запишіть як дріб, з 525 милями в чисельнику і 9 годин у знаменнику. $$\ dfrac {525\; миль} {9\; годин} $$
      $$\ dfrac {175\; миль} {3\; годин} $$

    Таким чином, 525 миль за 9 годин еквівалентно\(\dfrac{175\; miles}{3\; hours}\).

    Вправа\(\PageIndex{11}\):

    Запишіть ставку як дріб: 492 милі за 8 годин.

    Відповідь

    \(\dfrac{123\; miles}{2\; hours}\)

    Вправа\(\PageIndex{12}\):

    Запишіть ставку як дріб: 242 милі за 6 годин.

    Відповідь

    \(\dfrac{121\; miles}{3\; hours}\)

    Дописувачі та атрибуція