5.7: Розв'яжіть рівняння з десятковими числами
- Page ID
- 57922
- Визначте, чи десяткове число є розв'язком рівняння
- Розв'яжіть рівняння з десятковими числами
- Перевести на рівняння і вирішити
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Оцініть x +\(\dfrac{2}{3}\), коли x =\(− \dfrac{1}{4}\). Якщо ви пропустили цю проблему, перегляньте приклад 4.9.15.
- Оцінити 15 − y, коли y = −5. Якщо ви пропустили цю проблему, перегляньте приклад 3.6.12.
- Вирішити\(\dfrac{n}{−7}\) = 42. Якщо ви пропустили цю проблему, перегляньте приклад 4.12.5.
Визначте, чи десяткове число є розв'язком рівняння
Розв'язування рівнянь з десятковими числами важливо в нашому повсякденному житті, оскільки гроші зазвичай пишуться десятковими знаками. Коли програми передбачають гроші, такі як покупки для себе, складання бюджету вашої родини або планування майбутнього вашого бізнесу, ви будете вирішувати рівняння з десятковими знаками.
Тепер, коли ми працювали з десятковими числами, ми готові знайти рішення рівнянь із десятковими числами. Кроки, які ми робимо, щоб визначити, чи є число рішенням рівняння однакові, чи є розв'язком ціле число, ціле число, дріб або десяткове. Ми перерахуємо ці кроки тут ще раз для зручності довідки.
- Крок 1. Підставляємо число для змінної в рівняння.
- Крок 2. Спростіть вирази з обох сторін рівняння.
- Крок 3. Визначте, чи істинно отримане рівняння.
- Якщо так, то число - це рішення.
- Якщо ні, то число не є рішенням.
Визначте, чи є кожне з наступних розв'язків x − 0,7 = 1,5: (a) x = 1 (b) x = −0,8 (c) x = 2.2
Рішення
(А) х - 0,7 = 1,5
| \(\textcolor{red}{1}\)Замінюємо x. | $\ колір тексту {червоний} {1} - 0.7\ стек {?} {=} 1.5$$ |
| Відніміть. | $0.3\ нова 1.5$$ |
Оскільки x = 1 не призводить до істинного рівняння, 1 не є рішенням рівняння.
(б) х - 0,7 = 1,5
| \(\textcolor{red}{-0.8}\)Замінюємо x. | $\ колір тексту {червоний} {-0.8} - 0.7\ стек {?} {=} 1.5$$ |
| Відніміть. | $-1.5\ нова 1.5$$ |
Оскільки x = −0.8 не призводить до істинного рівняння, −0,8 не є розв'язком рівняння.
(в) х - 0,7 = 1,5
| \(\textcolor{red}{2.2}\)Замінюємо x. | $\ колір тексту {червоний} {2.2} - 0.7\ стековий {?} {=} 1.5$$ |
| Відніміть. | $1.5 = 1.5\;\ галочка $$ |
Оскільки x = 2.2 призводить до істинного рівняння, 2.2 є рішенням рівняння.
Визначте, чи є кожне значення розв'язком заданого рівняння. x − 0,6 = 1,3: (a) x = 0,7 (b) x = 1,9 (c) x = −0,7
- Відповідь на
-
ні
- Відповідь б
-
так
- Відповідь c
-
ні
Визначте, чи є кожне значення розв'язком заданого рівняння. y − 0,4 = 1,7: (a) y = 2.1 (b) y = 1.3 (c) −1.3
- Відповідь на
-
так
- Відповідь б
-
ні
- Відповідь c
- ні
Розв'яжіть рівняння з десятковими числами
У попередніх розділах ми розв'язували рівняння за допомогою Властивості рівності. Ці ж властивості ми будемо використовувати для вирішення рівнянь з десятковими числами.
|
Віднімання властивості рівності Для будь-яких чисел a, b і c, якщо a = b, то a − c = b − c. |
Додаткова властивість рівності Для будь-яких чисел a, b і c, якщо a = b, то a + c = b + c. |
|
Поділ власності рівності Для будь-яких чисел a, b, c і c ≠ 0 Якщо a = b, то\(\dfrac{a}{c} = \dfrac{b}{c}\) |
Властивість множення рівності Для будь-яких чисел a, b і c, Якщо a = b, то ac = bc |
Коли ви додаєте, віднімаєте, множите або ділите однакову величину з обох сторін рівняння, ви все одно маєте рівність.
Вирішити: y + 2.3 = −4,7.
Рішення
Ми будемо використовувати властивість віднімання рівності, щоб ізолювати змінну.
| Відніміть\(\textcolor{red}{2.3}\) з кожного боку, щоб скасувати додавання. | $$y+ 2.3\ колір тексту {червоний} {-2.3} = -4.7\ колір тексту {червоний} {-2.3} $$ |
| Спростити. | $$ у = -7$$ |
Перевірка:
| Замінюємо y =\(\textcolor{red}{-7}\). | $\ колір тексту {червоний} {-7} + 2.3\ стековий {?} {=} -4.7$$ |
| Спростити. | $$-4.7 = -4.7\;\ галочка $$ |
Оскільки y = −7 робить y + 2.3 = −4.7 справжнім твердженням, ми знаємо, що ми знайшли рішення цього рівняння.
Вирішити: y + 2.7 = −5,3.
- Відповідь
-
\(y=-8\)
Вирішити: y + 3,6 = −4,8.
- Відповідь
-
\(y=-8.4\)
Вирішити: a − 4,75 = −1,39.
Рішення
Ми будемо використовувати властивість додавання рівності.
| Додайте 4,75 до кожної сторони, щоб скасувати віднімання. | $a - 4,75\ колір тексту {червоний} {+4.75} = -1.39\ колір тексту {червоний} {+4.75} $$ |
| Спростити. | $А = 3.36$$ |
Перевірка:
| Замініть a =\(\textcolor{red}{3.36}\). | $\ колір тексту {червоний} {3.36} - 4.75\ стековий {?} {=} -1.39$$ |
| $-1.39 = -1.39\;\ галочка $$ |
Оскільки результат є істинним твердженням, a = 3.36 є рішенням рівняння.
Вирішити: a − 3.93 = −2.86.
- Відповідь
-
\(a=1.07\)
Вирішити: n − 3,47 = −2,64.
- Відповідь
-
\(n=0.83\)
Вирішити: −4.8 = 0.8n.
Рішення
Ми будемо використовувати властивість поділу рівності. Використовуйте Властивості рівності, щоб знайти значення для n.
| Ми повинні розділити обидві сторони на 0,8, щоб виділити n. | $$\ dfrac {-4.8} {\ колір тексту {червоний} {0.8}} =\ dfrac {0.8n} {\ textcolor {червоний} {08}} $$ |
| Спростити. | $-6 = н$$ |
Перевірка:
| Підставляємо n =\(\textcolor{red}{-6}\). | $-4.8\ стек {?} {=} 0.8 (\ колір тексту {червоний} {-6}) $$ |
| $$-4.8 = -4.8\;\ галочка $$ |
Оскільки n = −6 робить −4.8 = 0.8n істинним твердженням, ми знаємо, що у нас є рішення.
Вирішити: −8.4 = 0.7b.
- Відповідь
-
\(b=-12\)
Вирішити: −5,6 = 0.7c.
- Відповідь
-
\(c=-8\)
Вирішити:\(\dfrac{p}{−1.8}\) = −6,5.
Рішення
Ми будемо використовувати властивість множення рівності.
| Тут p ділиться на −1.8. Ми повинні помножити на −1.8, щоб виділити p. | $\ колір тексту {червоний} {-1.8}\ лівий (\ dfrac {p} {-1.8}\ праворуч) =\ колір тексту {червоний} {-1.8} (-6.5) $$ |
| Помножити. | $ $ р = 11.7$$ |
Перевірка:
| Підставляємо p =\(\textcolor{red}{11.7}\). | $\ drac {\ textcolor {червоний} {1.7}} {-1.8}\ стекер {?} {=} -6.5$$ |
| $$-6.5 = -6.5\;\ галочка $$ |
Розв'язок\(\dfrac{p}{−1.8}\) = −6,5 дорівнює p = 11,7.
Вирішити:\(\dfrac{c}{−2.6}\) = −4.5.
- Відповідь
-
\(c=-11.7\)
Вирішити:\(\dfrac{b}{−1.2}\) = −5.4.
- Відповідь
-
\(b=6.48\)
Перекласти на рівняння і вирішити
Тепер, коли ми розв'язали рівняння з десятковими числами, ми готові переводити словоречення в рівняння і вирішувати. Не забудьте шукати слова та фрази, які вказують на операції, які слід використовувати.
Перекласти і вирішити: Різниця n і 4.3 дорівнює 2,1.
Рішення
| Перекласти. | 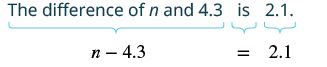 |
| Додайте 4.3 до обох сторін рівняння. | $n - 4.3\ колір тексту {червоний} {+4.3} = 2.1\ колір тексту {червоний} {+4.3} $$ |
| Спростити. | $$п = 6.4$$ |
Перевірка:
| Нехай n = 6,4. | Чи дорівнює різниця 6,4 і 4,3 2,1? |
| Перекласти. | $6.4 - 4.3\ стек {?} {=} 2.1$$ |
| Спростити. | $2.1 = 2.1\;\ галочка $$ |
Перекласти і вирішити: Різниця y і 4.9 дорівнює 2,8.
- Відповідь
-
\(y-4.9=2.8\);\(y=7.7\)
Перекласти і вирішити: Різниця z і 5.7 дорівнює 3,4.
- Відповідь
-
\(z-5.7=3.4\);\(z=9.1\)
Перекласти та розв'язати: добуток −3.1 та x дорівнює 5.27.
Рішення
| Перекласти. |  |
| Розділіть обидві сторони на −3.1. | $$\ dfrac {-3.1x} {\ textcolor {червоний} {-3.1}} =\ dfrac {5.27} {\ textcolor {червоний} {-3.1}} $$ |
| Спростити. | $ $ х = -1.7$$ |
Перевірка:
| Нехай x = −1.7. | Чи добуток −3.1 та −1.7 дорівнює 5,27? |
| Перекласти. | $-3.1 (-1.7)\ стек {?} {=} 5.27 $$ |
| Спростити. | $5.27 = 5.27\;\ галочка $$ |
Перекласти та розв'язати: добуток −4.3 та x дорівнює 12.04.
- Відповідь
-
\(-4.3x=12.04\);\(x=-2.8\)
Перекласти і розв'язати: добуток −3.1 і m дорівнює 26.66.
- Відповідь
-
\(-3.1m=26.66\);\(m=-8.6\)
Перекласти та розв'язати: Коефіцієнт p та −2.4 дорівнює 6,5.
Рішення
| Перекласти. |  |
| Помножте обидві сторони на −2.4. | $\ колір тексту {червоний} {-2.4}\ лівий (\ dfrac {p} {-2.4}\ праворуч) =\ колір тексту {червоний} {-2.4} (6.5) $$ |
| Спростити. | $р = -15.6$$ |
Перевірка:
| Нехай р = −15,6. | Чи є частка −15,6 та −2.4 дорівнює 6,5? |
| Перекласти. | $\ drac {\ колір тексту {червоний} {-15.6}} {-2.4}\ стекер {?} {=} 6.5$$ |
| Спростити. | $6,5 = 6.5\;\ галочка $$ |
Перекласти та розв'язати: Коефіцієнт q та −3.4 дорівнює 4.5.
- Відповідь
-
\(\frac{1}{-3.4}=4.5\);\(q=-15.3\)
Перекласти та розв'язати: Коефіцієнт r та −2.6 дорівнює 2.5.
- Відповідь
-
\(\frac{r}{-2.6}=2.5\);\(r=-6.5\)
Перекласти і розв'язати: Сума n і 2.9 дорівнює 1,7.
Рішення
| Перекласти. |  |
| Відніміть 2,9 з кожного боку. | $$n + 2.9\ колір тексту {червоний} {-2.9} = 1.7\ колір тексту {червоний} {-2.9} $$ |
| Спростити. | $$п = -1.2$$ |
Перевірка:
| Нехай n = −1,2. | Сума −1,2 та 2.9 дорівнює 1.7? |
| Перекласти. | $-1.2 + 2.9\ стек {?} {=} 1.7$$ |
| Спростити. | $1.7 = 1.7\;\ галочка $$ |
Перекласти і розв'язати: Сума j і 3.8 дорівнює 2,6.
- Відповідь
-
\(j+3.8=2.6\);\(j=-1.2\)
Перекласти і розв'язати: Сума k і 4.7 дорівнює 0,3.
- Відповідь
-
\(k+4.7=0.3\);\(k=-4.4\)
Практика робить досконалим
Визначте, чи десяткове число є розв'язком рівняння
У наступних вправах визначте, чи є кожне число розв'язком даного рівняння.
- x − 0.8 = 2,3
- х = 2
- х = −1,5
- х = 3,1
- у + 0,6 = −3,4
- y = −4
- y = −2,8
- у = 2,6
- \(\dfrac{h}{1.5}\)= −4,3
- ч = 6,45
- ч = −6,45
- h = −2,1
- 0,75к = −3,6
- k = −0,48
- k = −4,8
- k = −2,7
Розв'яжіть рівняння з десятковими числами
У наступних вправах розв'яжіть рівняння.
- у + 2,9 = 5,7
- м + 4,6 = 6,5
- ф + 3,45 = 2,6
- ч + 4,37 = 3,5
- а + 6,2 = −1.7
- б + 5,8 = −2,3
- с + 1,15 = −3,5
- д + 2,35 = −4,8
- n − 2,6 = 1.8
- p − 3,6 = 1.7
- x − 0.4 = −3.9
- y − 0.6 = −4.5
- j − 1.82 = −6.5
- k − 3.19 = −4.6
- м− 0.25 = −1.67
- q − 0.47 = −1.53
- 0,5х = 3,5
- 0.4р = 9,2
- −1,7c = 8,5
- −2,9х = 5,8
- −1,4р = −4,2
- −2,8м = −8,4
- −120 = 1,5кв
- −75 = 1,5г
- 0,24х = 4,8
- 0,18 = 5,4
- −3.4z = −9,18
- −2,7u = −9,72
- \(\dfrac{a}{0.4}\)= −20
- \(\dfrac{b}{0.3}\)= −9
- \(\dfrac{x}{0.7}\)= −0,4
- \(\dfrac{y}{0.8}\)= −0,7
- \(\dfrac{p}{−5}\)= −1,65
- \(\dfrac{q}{−4}\)= −5,92
- \(\dfrac{r}{−1.2}\)= −6
- \(\dfrac{s}{−1.5}\)= −3
Змішана практика
У наступних вправах розв'яжіть рівняння. Потім перевірте своє рішення.
- x − 5 = −11
- \(− \dfrac{2}{5}\)= х + (\ dfrac {3} {4}\)
- р + 8 = −2
- р +\(\dfrac{2}{3} = \dfrac{1}{12}\)
- −4,2м = −33,6
- q + 9,5 = −14
- q +\(\dfrac{5}{6} = \dfrac{1}{12}\)
- \(\dfrac{8.6}{15}\)= − d
- \(\dfrac{7}{8} m = \dfrac{1}{10}\)
- \(\dfrac{j}{−6.2}\)= −3
- \(− \dfrac{2}{3}\)= у +\(\dfrac{3}{8}\)
- s − 1.75 = −3.2
- \(\dfrac{11}{20}\)= − f
- −3,6б = 2,52
- −4,2а = 3,36
- −9.1n = −63,7
- r − 1,25 = −2.7
- \(\dfrac{1}{4} n = \dfrac{7}{10}\)
- \(\dfrac{h}{−3}\)= −8
- y − 7,82 = −16
Перекласти на рівняння і вирішити
У наступних вправах перекладіть і вирішуйте.
- Різниця n і 1,9 дорівнює 3,4.
- Різниця n і 1,5 становить 0,8.
- Добуток −6,2 і x дорівнює −4,96.
- Добуток −4,6 і x дорівнює −3.22.
- Коефіцієнт y та −1.7 дорівнює −5.
- Коефіцієнт z та −3.6 дорівнює 3.
- Сума n та −7,3 дорівнює 2,4.
- Сума n та −5.1 дорівнює 3,8.
Щоденна математика
- Шон купив пару взуття на продаж за 78 доларів. Вирішіть рівняння 0.75p = 78, щоб знайти початкову ціну взуття, стор.
- Мері купила новий холодильник. Загальна ціна, включаючи податок з продажу, становила 1,350 доларів. Знайти роздрібну ціну, r, холодильника до оподаткування, вирішивши рівняння 1.08r = 1,350.
Письмові вправи
- Подумайте про рішення рівняння 1.2y = 60, але насправді не вирішуйте його. Як ви вважаєте, рішення повинно бути більше 60 або менше 60? Поясніть свої міркування. Потім вирішіть рівняння, щоб побачити, чи правильно ваше мислення.
- Подумайте про рішення рівняння 0.8x = 200, але насправді не вирішуйте його. Як ви вважаєте, рішення повинно бути більше 200 або менше 200? Поясніть свої міркування. Потім вирішіть рівняння, щоб побачити, чи правильно ваше мислення.
Самостійна перевірка
(а) Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

(b) За шкалою 1—10, як би ви оцінили своє володіння цим розділом у світлі ваших відповідей на контрольний список? Як ви можете це покращити?
