Skip to main content
LibreTexts - Ukrayinska

8.2: Декартова система координат

  1. Last updated
  2. Save as PDF
  • Page ID
    57336

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Почнемо з поняття впорядкованої пари цілих чисел.

    Впорядковані пари цілих чисел

    Конструкція (x, y), де x і y - цілі числа, називається впорядкованою парою цілих чисел.

    Прикладами впорядкованих пар цілих чисел є (0, 0), (2, 3), (5, 1) і (4, 9).

    Порядок питань

    Особливу увагу зверніть на словосполучення «впорядковані пари». Порядок має значення. Отже, впорядкована пара (x, y) не збігається з упорядкованою парою (y, x), оскільки числа представлені в іншому порядку.

    Ми бачили, як побудувати цілі числа на числовому рядку. Наприклад, на малюнку 8.1 ми побудували цілі числа 2, 5 та 7 як затінені «точки» на числовій лінії.

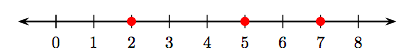
    Знімок екрана 2019-09-27 в 2.29.55 PM.png
    Малюнок 8.1: Покладання цілих чисел 2, 5 та 7 на числовому рядку.

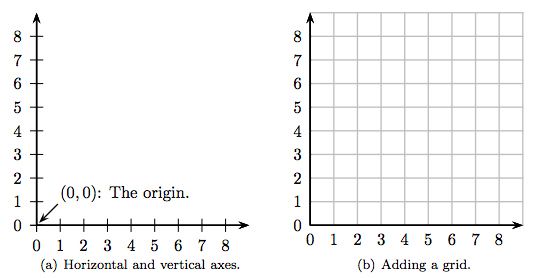
    Для побудови впорядкованих пар нам знадобляться дві числові лінії, звані горизонтальною і вертикальною осями, які перетинаються в нульовому розташуванні кожної лінії і знаходяться під прямим кутом одна до одної, як показано на малюнку 8.2 (а). Точка, де торкаються нульові місця, називається початком системи координат і має координати (0, 0). На малюнку 8.2 (b) ми додали сітку. Отримана конструкція є прикладом декартової системи координат.

    Знімок екрана 2019-09-27 о 2.30.01 PM.png
    Малюнок 8.2: Декартова система координат.

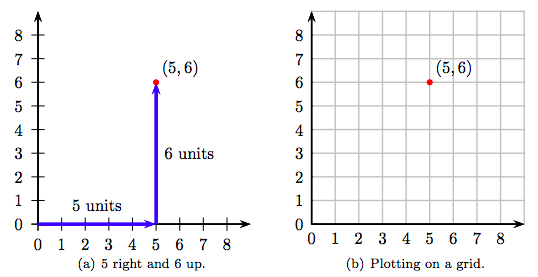
    Тепер розглянемо впорядковану пару цілих чисел (5, 6). Для побудови цієї точки на «системі координат» на малюнку 8.3 (a), почніть з початку (0, 0), потім перемістіть 5 одиниць у горизонтальному напрямку, потім 6 одиниць у вертикальному напрямку, потім нанесіть точку. Результат показаний на малюнку 8.3 (а). Додавання сітки горизонтальних і вертикальних ліній на кожне ціле число робить побудову точки (5, 6) набагато чіткіше, як показано на малюнку 8.3 (b).

    Знімок екрана 2019-09-27 о 2.30.55 PM.png
    Малюнок 8.3: Побудова точки (5, 6) у декартовій системі координат.

    Числа в упорядкованої парі (5, 6) називаються координатами нанесеної точки на малюнку 8.3 (б). Перше число впорядкованої пари називається абсцисою і вимірює горизонтальну відстань до нанесеної точки. Друге число називається ординатою і вимірює відстань по вертикалі до нанесеної точки. Поєднання осей і сітки на малюнку 8.3 (б) називається системою координат.

    Сітка на малюнку 8.3 (b) - це візуалізація, яка значно полегшує побудову впорядкованих пар. Однак вам не доведеться малювати ці лінії сітки самостійно. Замість цього слід працювати на графічному папері.

    Вимога до графічного паперу

    Вся побудова креслення повинна проводитися на графічному папері.

    Приклад 1

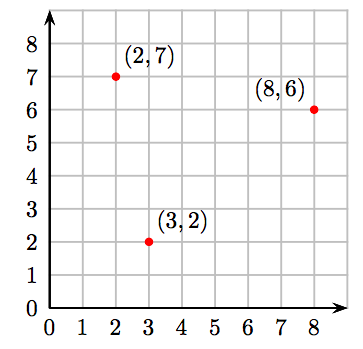
    Побудуйте наступні впорядковані пари цілих чисел: (3, 2), (8, 6), і (2, 7).

    Рішення

    Створіть декартову систему координат на графічному папері, а потім:

    • Для побудови впорядкованої пари (3, 2) почніть з початку, потім перемістіть 3 одиниці вправо і 2 одиниці вгору.
    • Для побудови впорядкованої пари (8, 6) почніть з початку, потім перемістіть 8 одиниць вправо і 6 одиниць вгору.
    • Для побудови впорядкованої пари (2, 7) почніть з початку, потім перемістіть 2 одиниці вправо і 7 одиниць вгору.

    Результати наведені на наступній декартовій системі координат.

    Знімок екрана 2019-09-27 у 1.58.14 PM.png

    Вправа

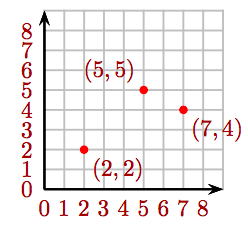
    Побудуйте наступні впорядковані пари цілих чисел: (2, 2), (5, 5) і (7, 4).

    Відповідь

    Знімок екрана 2019-09-27 в 1.58.08 PM.png

    Дозвіл для негативних чисел

    Знову ж таки, ми бачили, як побудувати як позитивні, так і негативні числа на числовому рядку. Наприклад, на малюнку 8.4 ми побудували числа −4, −3/2, 2.2 та 4.

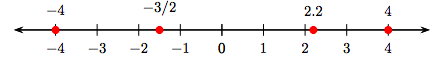
    Знімок екрана 2019-09-27 в 1.59.24 PM.png
    Рисунок 8.4: Побудова чисел −4, −3/2, 2.2 та 4.

    Зверніть увагу, що позитивний напрямок - вправо, негативне - зліва. Тобто, для побудови числа 2.2 ми переміщаємо 2,2 одиниці вправо на лінії, але для побудови числа −3/2 рухаємо вліво на 3/2 одиниці.

    Для побудови впорядкованих пар, що мають як додатне, так і від'ємне числа, нам знадобляться дві такі числові лінії, які перетинаються в нульовому розташуванні кожної лінії і знаходяться під прямим кутом один до одного, як показано на малюнку 8.5 (а). Як і раніше, додавання сітки горизонтальних і вертикальних ліній на кожне ціле число буде надзвичайно корисним при побудові точок (див. Рис. 8.5 (b)). Система осей та сітки на малюнку 8.5 (b) називається декартовою системою координат, названою на честь її винахідника Рене Декарта.

    Знімок екрана 2019-09-27 в 1.59.33 PM.png
    Малюнок 8.5: Декартова система координат.

    Побудова точок у декартовій системі координат

    На горизонтальній осі позитивний напрямок - вправо, негативне - вліво. На вертикальній осі позитивний напрямок - вгору, негативне - вниз. Точка (0, 0) називається початком системи координат і є початковою точкою для побудови всіх точок.

    Приклад 2

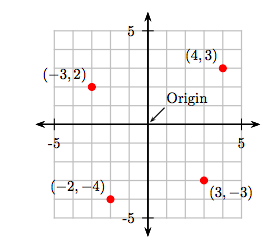
    Намалюйте точки (4, 3), (−3, 2), (−2, −4) та (3, −3) на декартовій системі координат.

    Рішення

    Налаштуйте декартову систему координат на графічному папері.

    • Для побудови точки (4, 3) почніть з початку, перемістіть 4 одиниці вправо, потім на 3 одиниці вгору.
    • Щоб побудувати точку (−3, 2), почніть з початку, перемістіть 3 одиниці вліво, потім на 2 одиниці вгору.
    • Щоб побудувати точку (−2, −4), почніть з початку, перемістіть 2 одиниці ліворуч, потім на 4 одиниці вниз.
    • Щоб побудувати точку (3, −3), почніть з початку, перемістіть 3 одиниці вправо, потім на 3 одиниці вниз.

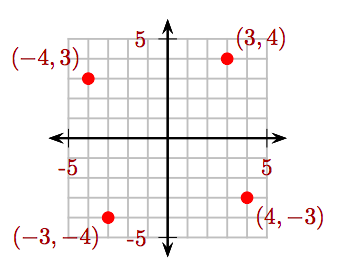
    Ці точки нанесені і показані на малюнку 8.6.

    Знімок екрана 2019-09-27 в 1.59.43 PM.png
    Малюнок 8.6: Побудова точок у декартовій системі координат.

    Вправа

    Намалюйте точки (3, 4), (−4, 3), (−3, −4) та (4, −3) на декартовій системі координат.

    Відповідь

    Знімок екрана 2019-09-27 у 1.59.52 PM.png

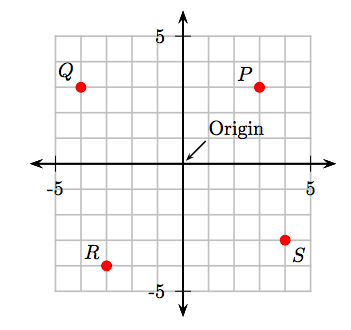
    Приклад 3

    Які координати точок P, Q, R і S в декартовій системі координат, яка слідує за нею?

    Знімок екрана 2019-09-27 в 2.00.02 PM.png

    Рішення

    Зробіть всі виміри від походження.

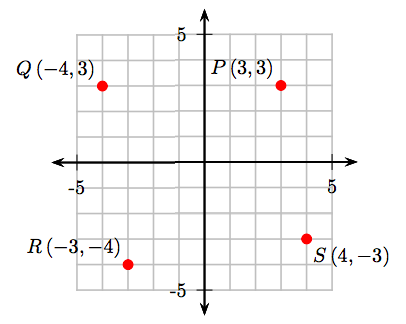
    • Щоб отримати координати точки Р, почніть з початку, перемістіть 3 одиниці вправо, потім на 3 одиниці вгору. Значить, координати точки Р є (3, 3).
    • Щоб отримати координати точки Q, почніть з початку, перемістіть 4 одиниці вліво, потім на 3 одиниці вгору. Отже, координати точки Q є (−4, 3).
    • Щоб отримати координати точки R, почніть з початку, перемістіть 3 одиниці вліво, потім 4 одиниці вниз. Отже, координати точки R є (−3, −4).
    • Щоб отримати координати точки S, почніть з початку, перемістіть 4 одиниці вправо, потім на 3 одиниці вниз. Отже, координати точки S є (4, −3).

    Ці результати показані на наступній декартовій системі координат.

    Знімок екрана 2019-09-27 в 2.00.12 PM.png

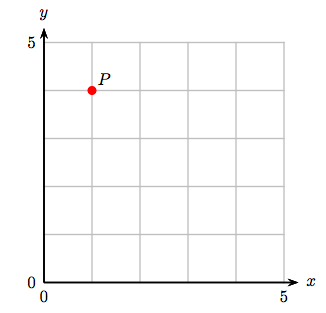
    Вправи

    1. Визначте координати точки Р.

    Знімок екрана 2019-09-27 у 2.22.07 PM.png

    2. Визначте координати точки Р.

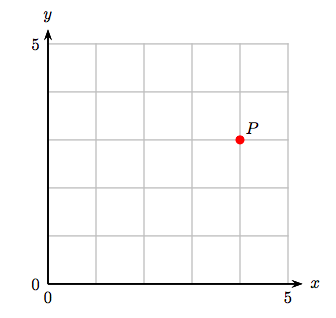
    Знімок екрана 2019-09-27 у 2.22.21 PM.png

    3. Визначте координати точки Р.

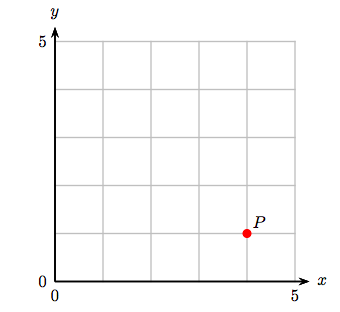
    Знімок екрана 2019-09-27 у 2.22.26 PM.png

    4. Визначте координати точки Р.

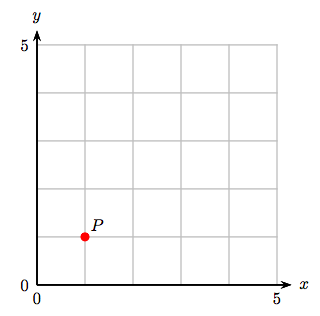
    Знімок екрана 2019-09-27 у 2.22.32 PM.png

    5. Визначте координати точки Р.

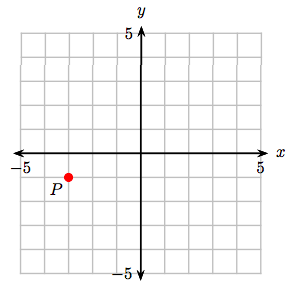
    Знімок екрана 2019-09-27 у 2.22.39 PM.png

    6. Визначте координати точки Р.

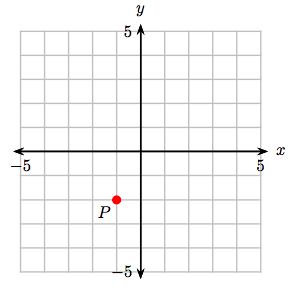
    Знімок екрана 2019-09-27 у 2.22.44 PM.png

    7. Визначте координати точки Р.

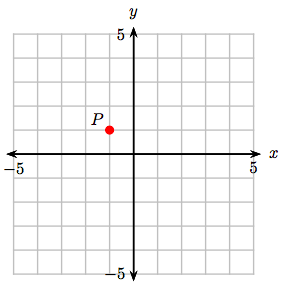
    Знімок екрана 2019-09-27 в 2.22.50 PM.png

    8. Визначте координати точки Р.

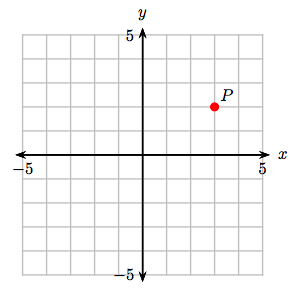
    Знімок екрана 2019-09-27 у 2.22.56 PM.png

    9. Точки A (−1, 1), B (1, 1), C (1, 2) та D (−1, 2) є вершинами прямокутника. Намалюйте ці точки, намалюйте прямокутник ABCD, потім обчислите площу прямокутника ABCD.

    10. Точки A (−3, −4), B (4, −4), C (4, −1) та D (−3, −1) є вершинами прямокутника. Намалюйте ці точки, намалюйте прямокутник ABCD, потім обчислите площу прямокутника ABCD.

    11. Точки A (−2, −1), B (3, −1), C (3, 3) та D (−2, 3) є вершинами прямокутника. Намалюйте ці точки, намалюйте прямокутник ABCD, потім обчислите площу прямокутника ABCD.

    12. Точки A (−3, −1), B (2, −1), C (2, 2) та D (−3, 2) є вершинами прямокутника. Намалюйте ці точки, намалюйте прямокутник ABCD, потім обчислите площу прямокутника ABCD.

    13. Точки A (−4, −2), B (1, −2), C (1, 1) та D (−4, 1) є вершинами прямокутника. Намалюйте ці точки, намалюйте прямокутник ABCD, потім обчислите периметр прямокутника ABCD.

    14. Точки A (−4, −4), B (1, −4), C (1, −3) та D (−4, −3) є вершинами прямокутника. Намалюйте ці точки, намалюйте прямокутник ABCD, потім обчислите периметр прямокутника ABCD.

    15. Точки A (−1, 2), B (3, 2), C (3, 3) та D (−1, 3) є вершинами прямокутника. Намалюйте ці точки, намалюйте прямокутник ABCD, потім обчислите периметр прямокутника ABCD.

    16. Точки A (−4, 2), B (3, 2), C (3, 4) та D (−4, 4) є вершинами прямокутника. Намалюйте ці точки, намалюйте прямокутник ABCD, потім обчислите периметр прямокутника ABCD.

    17. Точки A (−3, −1), B (1, −1) та C (−3, 0) є вершинами трикутника. Побудуйте ці точки, намалюйте трикутник ABC, потім обчислите площу трикутника ABC.

    18. Точки A (−3, −2), B (1, −2) та C (−3, 2) є вершинами трикутника. Побудуйте ці точки, намалюйте трикутник ABC, потім обчислите площу трикутника ABC.

    19. Точки A (−1, −2), B (0, −2) та C (−1, 0) є вершинами трикутника. Побудуйте ці точки, намалюйте трикутник ABC, потім обчислите площу трикутника ABC.

    20. Точки A (−2, −3), B (−1, −3) та C (−2, 1) є вершинами трикутника. Побудуйте ці точки, намалюйте трикутник ABC, потім обчислите площу трикутника ABC.

    21. Покладіть точки A (−3, −3) та B (0, 0) та знайдіть відстань по прямій лінії між двома точками. Підказка: Створіть прямокутний трикутник, а потім скористайтеся теоремою Піфагора.

    22. Покладіть точки A (−2, −3) та B (1, 2) та знайдіть пряму відстань між двома точками. Підказка: Створіть прямокутний трикутник, а потім скористайтеся теоремою Піфагора.

    23. Покладіть точки A (−2, −3) та B (0, 0) та знайдіть пряму відстань між двома точками. Підказка: Створіть прямокутний трикутник, а потім скористайтеся теоремою Піфагора.

    24. Покладіть точки A (−3, −2) та B (2, 2) та знайдіть пряму відстань між двома точками. Підказка: Створіть прямокутний трикутник, а потім скористайтеся теоремою Піфагора.

    25. Знайдіть площу затіненого трикутника.

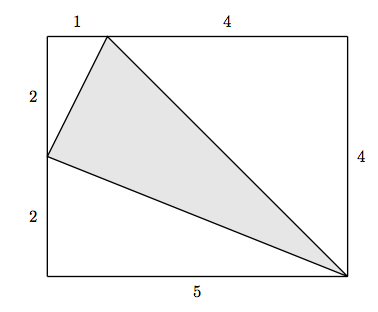
    Знімок екрана 2019-09-27 у 2.10.48 PM.png

    26. Знайдіть площу затіненого трикутника.

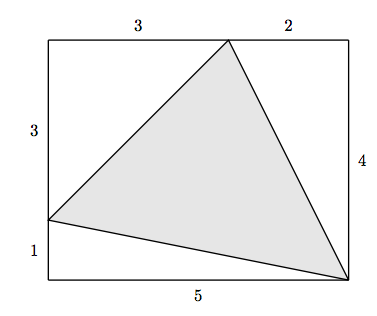
    Знімок екрана 2019-09-27 у 2.10.54 PM.png

    27. Знайдіть площу затіненого трикутника.

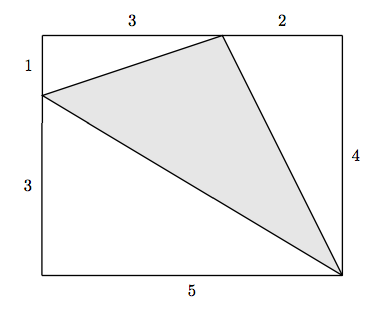
    Знімок екрана 2019-09-27 у 2.10.59 PM.png

    28. Знайдіть площу затіненого трикутника.

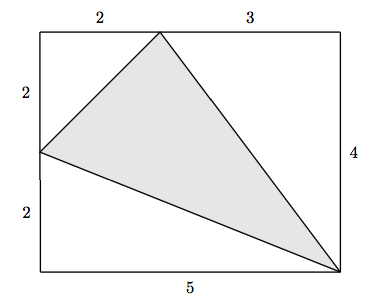
    Знімок екрана 2019-09-27 в 2.11.03 PM.png

    Підказка: У вправах 29-32 об'єднайте трикутник прямокутником, як показано у вправах 25-28.

    29. Знайти площу трикутника з вершинами на A (−4, −1), B (4, −2) та C (1, 3).

    30. Знайдіть площу трикутника з вершинами на A (−4, 2), B (3, 0) та C (0, 4).

    31. Знайти площу трикутника з вершинами на A (−3, 1), B (3, −3) та C (1, 4).

    32. Знайдіть площу трикутника з вершинами на A (1, 2), B (3, 0) та C (2, 4).

    Відповіді

    1. (1, 4)

    3. (4, 1)

    5. (−3, −1)

    7. (−1, 1)

    9. 2 квадратних одиниці

    11. 20 квадратних одиниць

    13. 16 одиниць

    15. 10 одиниць

    17. 2 квадратних одиниці

    19. 1 квадратні одиниці

    21. \(\sqrt{18}\)

    23. \(\sqrt{13}\)

    25. 6

    27. 7

    29. \(\frac{37}{2}\)

    31. 17