6.5: Зворотні функції

Для цього розділу ми будемо використовувати поняття декартового добутку двох множин\(A\) і\(B\), позначається тим\(A \times B\), який є множиною всіх впорядкованих пар\((x, y)\) де\(x \in A\) і\(y \in B\). Тобто,

\(A \times B = \{(x, y)\ |\ x \in A \text{ and } y \in B\}.\)

Докладніше про цю концепцію див. розділ Перегляд дій\(\PageIndex{2}\) у розділі 5.4.

АКТИВНІСТЬ ПОПЕРЕДНЬОГО ПЕРЕГЛЯДУ\(\PageIndex{1}\): Functions and Sets of Ordered Pairs

Коли ми графуємо реальну функцію, ми будуємо впорядковані пари в декартовій площині, де перша координата є входом функції, а друга координата є виходом функції. Наприклад, якщо\(g: \mathbb{R} \to \mathbb{R}\), то кожна точка на графіку\(g\) являє собою впорядковану пару\((x, y)\) дійсних чисел де\(y = g(x)\). Це показує, як ми можемо генерувати впорядковані пари з функції. Буває, що ми можемо це зробити за допомогою будь-якої функції. Наприклад, нехай

\(A = \{1, 2, 3\}\)і\(B = \{a, b\}\).

Визначте функцію\(F: A \to B\) за

\(F(1) = a\),\(F(2) = b\), і\(F(3) = b\).

Ми можемо перетворити кожну з них в впорядковану пару,\(A \times B\) використовуючи вхід як першу координату, а вихід як другу координату. Наприклад,\(F(1) = a\) перетворюється в\((1, a)\),\(F(2) = b\) перетворюється на\((2, b)\) і\(F(3) = b\) перетворюється в\((3, b)\). Таким чином, ми можемо думати про цю функцію як набір впорядкованих пар, який є підмножиною\(A \times B\), і писати

\(F = \{(1, a), (2, b), (3, b)\}.\)

Примітка: Оскільки\(F\) це назва функції, її прийнято використовувати\(F\) як ім'я для множини впорядкованих пар.

1. Нехай\(A = \{1, 2, 3\}\) і нехай\(C = \{a, b, c, d\}\). Визначте функцію\(g: A \to C\) по\(g(1) = a\)\(g(2) = b\), і\(g(3) = d\). Запишіть функцію\(g\) як набір впорядкованих пар в\(A \times C\).

Для іншого прикладу, якщо у нас є реальна функція, така як:\(g: \mathbb{R} \to \mathbb{R}\) by\(g(x) = x^2 - 2\), то ми можемо думати про\(g\) таку нескінченну підмножину\(\mathbb{R} \times \mathbb{R}\):

\(g = \{(x, y) \in \mathbb{R} \times \mathbb{R}\ |\ y = x^2 - 2\}.\)

Ми також можемо написати це іноді писати це як\(g = \{(x, x^2 - 2)\ |\ x \in \mathbb{R}\}.\)

2. Дозвольте\(f: \mathbb{Z} \to \mathbb{Z}\) визначитися\(f(m) = 3m + 5\), для всіх\(m \in \mathbb{Z}\). Використовуйте нотацію set builder, щоб записати функцію\(f\) як набір впорядкованих пар, а потім використовуйте метод реєстру, щоб записати функцію\(f\) як набір впорядкованих пар.

Таким чином, будь-яка функція\(f: A \to B\) може бути розглянута як набір впорядкованих пар, що є підмножиною\(A \times B\). Ця підмножина

\(f = \{(a, f(a))\ |\ a \in A\}\)або\(f = \{(a, b) \in A \times B\ |\ b = f(a)\}.\)

З іншого боку, якщо ми починали з\(A = \{1, 2, 3\}\)\(B = \{a, b\}\), і

\(G = \{(1, a), (2, a), (3, b)\} \subseteq A \times B,\)

то ми могли б думати про функції від\(A\) до\(B\) з\(G(1) = a\)\(G(2) = a\), і\(G(3) = b\).\(G\) Ідея полягає в тому, щоб використовувати першу координату кожної впорядкованої пари як вхідні дані, а другу координату як вихід. Однак не кожна підмножина\(A \times B\) може бути використана для визначення функції від\(A\) до\(B\). Це досліджується в наступних питаннях.

3. Нехай\(f = \{(1, a), (2, a), (3, a), (1, b)\}\). Чи може цей набір впорядкованих пар бути використаний для визначення функції від\(A\) до\(B\)? Поясніть.
4. Нехай\(g = \{(1, a), (2, a), (3, a)\}\). Чи може цей набір впорядкованих пар бути використаний для визначення функції від\(A\) до\(B\)? Поясніть.
5. Нехай\(h = \{(1, a), (2, b)\}\). Чи може цей набір впорядкованих пар бути використаний для визначення функції від\(A\) до\(B\)? Поясніть.

АКТИВНІСТЬ ПОПЕРЕДНЬОГО ПЕРЕГЛЯДУ\(\PageIndex{1}\): A Composition of Two Specific Functions

Нехай\(A = \{a, b, c, d\}\) і нехай\(B = \{p, q, r, s\}\).

1. Побудувати приклад функції\(f: A \to B\), яка є біекцією. Намалюйте діаграму зі стрілками для цієї функції.
2. На діаграмі зі стрілками намалюйте стрілку від кожного елемента\(B\) спини до відповідного елемента в\(A\). Поясніть, чому це визначає функцію\(B\) from to\(A\).
3. Якщо ім'я функції в Part (2) є\(g\), так що\(g: B \to A\), які\(g(p)\),,\(g(q)\),\(g(r)\), і\(g(s)\)?
4. Побудувати таблицю значень для кожної з функцій\(g \circ f: A \to A\) і\(f \circ g: B \to B\). Що ви спостерігаєте щодо цих таблиць значень?

Представлення впорядкованої пари функції

У Preview Activity ми помітили\(\PageIndex{1}\), що якщо у нас є функція\(f: A \to B\), ми можемо генерувати набір впорядкованих пар\(f\), який є підмножиною\(A \times B\) наступним чином:

\(f = \{(a, f(a)\ |\ a \in A\}\)або\(f = \{(a, b) \in A \times B\ |\ b = f(a)\}.\)

Однак ми також дізналися, що деякі набори впорядкованих пар не можуть бути використані для визначення функції. Тепер ми хочемо вивчити, за яких умов набір впорядкованих пар може бути використаний для визначення функції. Починаючи з функції\(f: A \to B\), оскільки dom (\(f\)) =\(A\), ми знаємо, що

\[\text{For every } a \in A \text{, there exists a } b \in B \text{ such that } (a, b) \in f. \label{6.5.1}\]

Зокрема, ми використовуємо\(b = f(a)\). Це говорить про те, що кожен елемент\(A\) може бути використаний в якості вхідних даних. Крім того, щоб бути функцією, кожен вхід може видавати тільки один вихід. З точки зору впорядкованих пар це означає, що ніколи не буде двох впорядкованих пар\((a, b)\) і\((a, c)\) в функції\(f\) де\(a \in A\)\(b, c \in B\), і\(b \ne c\). Ми можемо сформулювати це як умовне твердження наступним чином:

\[\text{For every } a \in A \text{ and every } b, c \in B, \\ \text{if } (a, b) \in f \text{ and } (a,c) \in f \text{, then } b = c. \label{6.5.2}\]

Це також означає, що якщо ми почнемо з\(f\) підмножини\(A \times B\), яка задовольняє умовам у Equation\ ref {6.5.1} та\ ref {6.5.2}, то ми можемо вважати\(f\) функцією від\(A\) до,\(B\) використовуючи\(b = f(a)\) всякий раз, коли\((a, b)\) знаходиться в\(f\). Це доводить наступна теорема.

Теорема 6.22

Дозволяти\(A\) і\(B\) бути непорожніми множинами і нехай\(f\) бути підмножиною\(A \times B\), що задовольняє наступним двом властивостям:

• Для кожного існує\(b \in B\) таке\(a \in A\), що\((a, b) \in f\); і
• Для кожного\(a \in A\)\(b, c \in B\), якщо\((a, b) \in f\) і\((a, c) \in f\), то\(b = c\).

Якщо ми використовуємо\(f(a) = b\) щоразу\((a, b) \in f\), то\(f\) є функцією від\(A\) до\(B\).

Примітка про теорему 6.22. Перша умова в теоремі 6.22 означає, що кожен елемент A є входом, а друга умова гарантує, що кожен вхід має рівно один вихід. Багато текстів використовуватимуть теорему 6.22 як визначення функції. Багато математиків вважають, що це впорядковане парне подання функції є найбільш суворим визначенням функції. Це дозволяє нам використовувати теорію множин для роботи з функціями та порівняння. Наприклад, рівність функцій стає питанням рівності множин. Тому багато підручників використовуватимуть упорядковане парне представлення функції як визначення функції.

Перевірка прогресу 6.23 (набори впорядкованих пар, які не є функціями)

Нехай\(A = \{1, 2, 3\}\) і нехай\(B = \{a, b\}\). Поясніть, чому кожна з наступних підмножин\(A \times B\) не може бути використана для визначення функції від\(A\) до\(B\).

1. \(F = \{(1, a), (2, a)\}\),
2. \(G = \{(1, a), (2, b), (3, c), (2, c)\}\).

Відповідь

Додайте сюди тексти. Не видаляйте цей текст спочатку.

Обернена функція

На попередніх курсах математики ми дізналися, що експоненціальна функція (з базою\(e\)) та функції натурального логарифма є оберненнями один одного. Це часто виражалося наступним чином:

Для кожного\(x \in R\) з\(x > 0\) і для кожного\(y \in \mathbb{R}\),\(y = \text{ln}x\) якщо і тільки якщо\(x = e^y\).

Зверніть увагу, що\(x\) це означає, що це вхід і\(y\) є виходом для функції натурального логарифма тоді і тільки тоді, коли\(y\) є входом і\(x\) є виходом для експоненціальної функції. По суті, обернена функція (в даному випадку експоненціальна функція) змінює дію початкової функції (в даному випадку функції натурального логарифма). У терміні впорядкованих пар (пар введення-виведення) це означає, що якщо\((x, y)\) є впорядкованою парою для функції, то\((y, x)\) є впорядкованою парою для її оберненої. Ця ідея зміни ролей першої та другої координат є основою для нашого визначення зворотної функції.

Визначення: Обернена функція

\(f: A \to B\)Дозволяти бути функцією. Обернене\(f\), позначається\(f^{-1}\), являє собою набір впорядкованих пар\(\{(b, a) \in B \times A\ |\ f(a) = b\}\). Тобто,

\(f^{-1} = \{(b, a) \in B \times A\ |\ f(a) = b\}\).

Якщо ми використовуємо впорядковане представлення пари для\(f\), ми могли б також написати

\(f^{-1} = \{(b, a) \in B \times A\ |\ (a, b) \in f\}\).

Зверніть увагу, що це визначення не стверджує, що\(f^{-1}\) є функцією. Це просто підмножина\(B \times A\). Після того, як ми вивчимо матеріал в главі 7, скажемо, що\(f^{-1}\) це означає, що є відношення від\(B\) до\(A\). Цей факт, однак, не важливий для нас зараз. Нас цікавить в основному наступне питання:

За яких умов обернена функція\(f: A \to B\) буде функцією від\(B\) до\(A\)?

Перевірка прогресу 6.24: Вивчення зворотної функції

Нехай\(A = \{a, b, c\}\),\(B = \{a, b, c, d\}\), і\(C = \{p, q, r\}\). Визначте

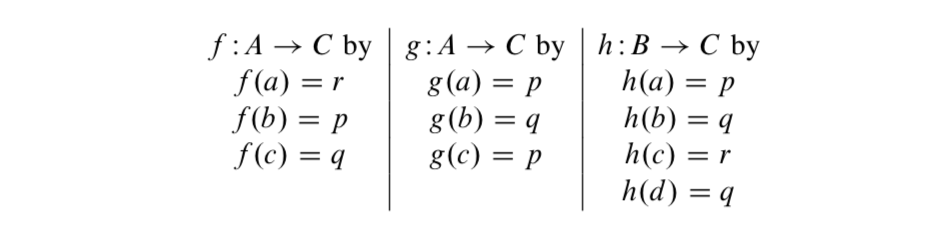
1. Намалюйте діаграму зі стрілками для кожної функції.
2. Визначте обернену кожну функцію як набір впорядкованих пар.
3. (a) Чи\(f^{-1}\) є функція від\(C\) до\(A\)? Поясніть.
   (b) Чи\(g^{-1}\) є функція від\(C\) до\(A\)? Поясніть.
   (c) Чи\(h^{-1}\) є функція від\(C\) до\(B\)? Поясніть.
4. Намалюйте діаграму зі стрілками для кожної оберненої частини (3), яка є функцією. Використовуйте існуючу діаграму зі стрілками з частини (1), щоб намалювати цю діаграму зі стрілками.
5. Складіть здогадки про те, які умови на функції\(F: S \to T\) забезпечать, що її зворотна є функцією від\(T\) до\(S\).

Відповідь

Додайте сюди тексти. Не видаляйте цей текст спочатку.

Зараз ми розглянемо загальний аргумент, запропонований дослідженнями в Progress Check 6.24. За визначенням, якщо\(f: A \to B\) є функцією, то\(f^{-1}\) є підмножиною\(B \times A\). Однак\(f^{-1}\) може бути або не бути функцією від\(B\) до\(A\). Наприклад, припустимо, що\(s, t \in A\) з\(s \ne t\) і\(f(s) = f(t)\). Це представлено на малюнку 6.9.

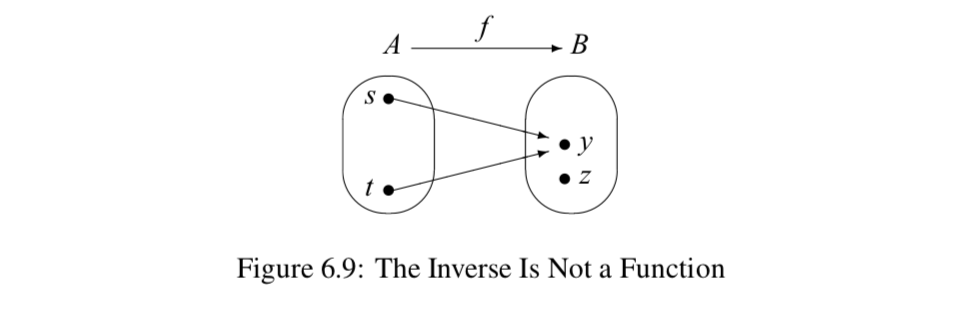
В цьому випадку, якщо ми спробуємо повернути стрілки назад, ми не отримаємо функцію від\(B\) до\(A\). Це тому, що\((y, s) \in f^{-1}\) і\((y, t) \in f^{-1}\) з\(s \ne t\). Отже, не\(f^{-1}\) є функцією. Це говорить про те,\(f\) що коли не ін'єкція, то не\(f^{-1}\) є функцією.

Також якщо не\(f\) відсмоктування, то існує\(z \in B\) таке, що\(f(a) \ne z\) для всіх\(a \in A\), як на схемі на малюнку 6.9. Іншими словами, немає впорядкованої пари в\(f\) with\(z\) як друга координата. Це означає, що не було б впорядкованої пари в\(f^{-1}\) з\(z\) першою координатою. Отже,\(f^{-1}\) не може бути функцією від\(B\) до\(A\).

Це мотивує твердження в теоремі 6.25. На доказ цієї теореми ми часто змінюватимемо назад і вперед від представлення функції на вході-виході та впорядкованого парного представлення функції. Ідея полягає в тому, що якщо\(G: S \to T\) це функція, то для\(s \in S\) і\(t \in T\),

\(G(s) = t\)якщо і тільки якщо\((s, t) \in G\).

Коли ми використовуємо впорядковане парне представлення функції, ми також будемо використовувати впорядковане парне представлення її оберненої. У цьому випадку ми знаємо, що

\((s, t) \in G\)якщо і тільки якщо\((t, s) \in G^{-1}\).

Теорема 6.25.

\(B\)Дозволяти\(A\) і бути непорожніми множинами і нехай\(f: A \to B\). Обернене\(f\) - це функція від\(B\) до\(A\) якщо і тільки тоді, коли\(f\) є біекцією.

Доказ

\(B\)Дозволяти\(A\) і бути непорожніми множинами і нехай\(f: A \to B\). Спочатку припустимо, що f - це біекція і доведемо, що\(f^{-1}\) є функцією від\(B\) до\(A\). Для цього ми покажемо, що\(f^{-1}\) задовольняє двом умовам теореми 6.22.

Спочатку вибираємо\(b \in B\). Так як функція\(f\) є surjection, існує\(a \in A\) таке, що\(f(a) = b\). Це означає, що\((a, b) \in f\) і, отже, що\((b, a) \in f^{-1}\). Таким чином, кожен елемент\(B\) є першою координатою впорядкованої пари в\(f^{-1}\), а отже,\(f^{-1}\) задовольняє першій умові Теореми 6.22.

Щоб довести, що\(f^{-1}\) відповідає другій умові теореми 6.22, ми повинні показати, що кожен елемент\(B\) є першою координатою рівно однієї впорядкованої пари в\(f^{-1}\). Так давайте\(b \in B\),\(a_1, a_2 \in A\) і припустимо, що

\((b, a_1) \in f^{-1}\)і\((b, a_2) \in f^{-1}\).

Це означає, що\ ((a_1, b)\ in f) і\ ((a_2, b)\ in f). Потім ми можемо зробити висновок, що

\(f(a_1) = b\)і\(f(a_2) = b\).

Але це означає, що\(f(a_1) = f(a_2)\). Оскільки\(f\) це біекція, то це ін'єкція, і ми можемо зробити висновок, що\(a_1 = a_2\). Це доводить, що\(b\) є першим елементом тільки однієї впорядкованої пари в\(f^{-1}\). Отже, доведено, що\(f^{-1}\) задовольняє обом умовам теореми 6.22 і, отже,\(f^{-1}\) це функція від\(B\) до\(A\).

Тепер ми припускаємо, що\(f^{-1}\) є функцією\(A\) і\(B\) довести, що\(f\) це біекція. По-перше, щоб довести, що\(f\) це ін'єкція, ми припускаємо, що\(a_1, a_2 \in A\) і що\(f(a_1) = f(a_2)\). Ми хочемо це показати\(a_1 = a_2\). Якщо ми дозволимо\(b = f(a_1) = f(a_2)\), то можна зробити висновок, що

\ ((a_1, b)\ в f) і\ ((a_2, b)\ в f).

Але це означає, що

\((b, a_1) \in f^{-1}\)і\((b, a_2) \in f^{-1}\).

Оскільки ми припустили, що\(f^{-1}\) це функція, ми можемо зробити висновок, що\(a_1 = a_2\). Значить, f - це ін'єкція.

Тепер, щоб довести, що\(f\) це відмова, ми виберемо\(b \in B\) і покажемо, що існує\(a \in A\) таке, що\(f(a) = b\). Оскільки\(f^{-1}\) це функція,\(b\) повинна бути першою координатою якоїсь впорядкованої пари в\(f^{-1}\). Отже, існує\(a \in A\) таке, що

\((b, a) \in. f^{-1}\).

Тепер це означає, що\((a, b) \in f\) і, отже, що\(f(a) = b\). Це доводить, що\(f\) це відмова. Оскільки ми також довели, що\(f\) це ін'єкція, робимо висновок, що\(f\) це біекція.

Обернене позначення функції

У ситуації, коли\(f: A \to B\) є біекція і\(f^{-1}\) є функцією від\(B\) до\(A\), ми можемо писати\(f^{-1}: B \to A\). У цьому випадку ми часто говоримо, що\(f\) це оборотна функція, і ми зазвичай не використовуємо впорядковане представлення пари ні для одного\(f\) або\(f^{-1}\). Замість того, щоб писати\((a, b) \in f\), ми пишемо\(f(a) = b\), а замість того, щоб писати\((b, a) \in. f^{-1}\), пишемо\(f^{-1}(b) = a\). Використовуючи той факт, що\((a, b) \in f\) якщо і тільки якщо\((b, a) \in. f^{-1}\), ми можемо тепер писати\(f(a) = b\) якщо і тільки якщо\(f^{-1}(b) = a\). Підсумовуємо це в теоремі 6.26.

Теорема 6.26

Дозволяти\(A\) і\(B\) бути непорожніми\(f: A \to B\) множинами і нехай бути біекцією. Тоді\(f^{-1}: B \to A\) є функція, причому для кожного\(a \in A\) і\(b \in B\).

\(f(a) = b\)якщо і тільки якщо\(f^{-1}(b) = a\).

Приклад 6.27: Зворотні позначення функції

Для прикладу використання позначення в теоремі 6.26, нехай\(\mathbb{R}^{+} = \{x \in \mathbb{R}\ |\ x>0\}\). Визначте

\(f: \mathbb{R} \to \mathbb{R}\)по\(f(x) = x^3\); і\(g: \mathbb{R} \to \mathbb{R}^{+}\) по\(g(x) = e^x\).

Зверніть увагу, що\(\mathbb{R}^{+}\) це кодомен\(g\). Тоді ми можемо сказати, що обидва\(f\) і\(g\) є двосторонніми. Отже, зворотні ці функції також є функціями. Фактично,

\(f^{-1}: \mathbb{R} \to \mathbb{R}\)по\(f^{-1}(y) = \sqrt[3] {y}\); і\(g^{-1}: \mathbb{R}^{+} \to \mathbb{R}\) по\(g^{-1}(y) = \text{In}y\).

Для кожної функції (і її оберненої) ми можемо записати результат теореми 6.26 наступним чином:

Теореми про обернені функції

Наступні два результати в цьому розділі - дві важливі теореми про обернені функції. Перший насправді є наслідком теореми 6.26.

Слідство 6.28.

Дозволяти\(A\) і\(B\) бути непорожніми множинами і нехай\(f: A \to B\) бути bijection. Тоді

1. Для кожного\(x\) в\(A\),\((f^{-1} \circ f)(x) = x\)).
2. Для кожного\(y\) в\(B\),\((f \circ f^{-1})(y) = y\)).

Доказ

Дозволяти\(A\) і\(B\) бути непорожніми множинами і припустити, що\(f: A \to B\) це біекція. Так нехай\(x \in A\) і нехай\(f(x) = y\). За теоремою 6.26 можна зробити висновок, що\(f^{-1}(y) = x\). Тому,

\[\begin{array} {rcl} {(f^{-1} \circ f)(x)} &= & {f^{-1}(f(x))} \\ {} &= & {f^{-1}(y}} \\ {} &= & {x.} \end{array}\]

Значить, для кожного\(x \in A\),\((f^{-1} \circ f)(x) = x\)).

Доказом того, що для кожного\(y\) в\(B\),\((f \circ f^{-1})(y) = y\)) є Вправа (4).

Приклад 6.27 (продовження)

Для функції кубінгу та функції кореня куба ми бачили, що

Для\(x, y \in \mathbb{R}\),\(x^3 = y\) якщо і тільки якщо\(\sqrt[3]{y} = x\).

Зауважте, що

• Якщо підставити\(x^3 = y\) в рівняння\(\sqrt[3]{y} = x\), то отримаємо\(\sqrt[3]{x^3} = x\).
• Якщо підставити\(\sqrt[3]{y} = x\) в рівняння\(x^3 = y\), то отримаємо\((\sqrt[3]{y})^3 = y\).

Це ілюстрація Слідство 6.28. Ми можемо побачити це, використовуючи\(f: \mathbb{R} \to \mathbb{R}\)\(f(x) = x^3\) визначені і\(f^{-1}: \mathbb{R} \to \mathbb{R}\) визначені\(f^{-1}(y) = \sqrt[3]{y}\). Потім\(f^{-1} \circ f: \mathbb{R} \to \mathbb{R}\) і\(f^{-1} \circ f = I_{\mathbb{R}}\),

\[\beign{array} {rcl} [(f^{-1} \circ f)(x)} &= & {x} \\ {f^{-1}(f(x))} &= & {x} \\ {f^{-1}(x^3)} &= & {x} \\ {\sqrt[3]{x^3}} &= & {x.} \end{array}\]

Аналогічно рівняння\((\sqrt[3]{y})^3 = y\) для кожного\(y \in \mathbb{R}\) можна отримати з того, що для кожного\(y \in \mathbb{R}\),\((f \circ f^{-1})(y) = y\)).

Ми зараз розглянемо випадок, коли\(f: A \to B\) і\(g: B \to C\) є обидва біекції. В даному випадку\(f^{-1}: B \to A\) і\(g^{-1}: C \to B\). Малюнок 6.10 може бути використаний для ілюстрації цієї ситуації.

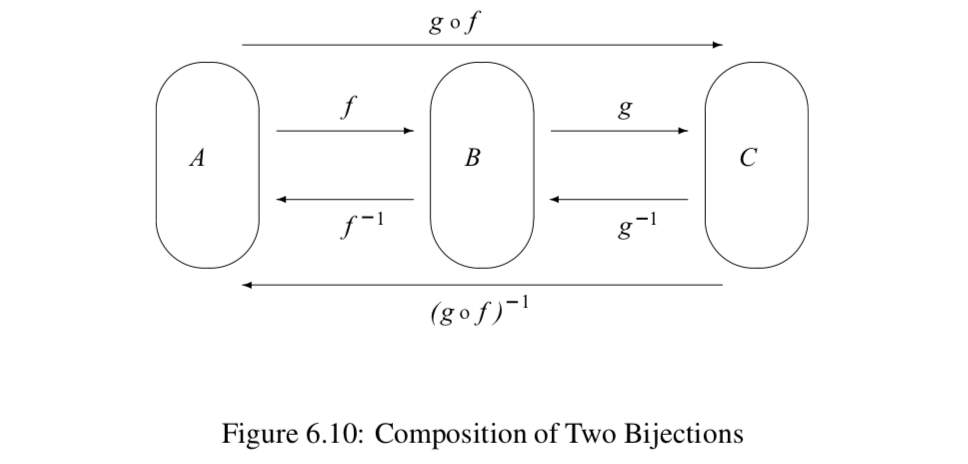
За теоремою 6.20, також\(g \circ f: A \to C\) є біекцією. Отже, за теоремою 6.25,\((g \circ f)^{-1}\) є функцією і, власне,\((g \circ f)^{-1}: C \to A\). Зверніть увагу, що ми також можемо сформувати склад з\(g^{-1}\) подальшим\(f^{-1}\), щоб отримати\(f^{-1} \circ g^{-1}: C \to A\). Малюнок 6.10 допомагає проілюструвати результат наступної теореми.

Теорема 6.29.

Нехай\(f: A \to B\) і\(g: B \to C\) будуть упередження. Потім\(g \circ f\) йде біекція і\((g \circ f)^{-1} = f^{-1} \circ g^{-1}\).

Доказ

Нехай\(f: A \to B\) і\(g: B \to C\) будуть упередження. Потім\(f^{-1}: B \to A\) і\(g^{-1}: C \to B\). Отже,\(f^{-1} \circ g^{-1}: C \to A\). Крім того, за теоремою 6.20,\(g \circ f: A \to C\) є біекцією, а значить\((g \circ f)^{-1}: C \to A\). Ми зараз доведемо, що для кожного\(z \in C\),\((g \circ f)^{-1}(z) = f^{-1} \circ g^{-1}(z)\).

Нехай\(z \in C\). Так як функція\(g\) є surjection, існує\(y \in B\) таке, що

\[g(y) = z.\]

Також, оскільки\(f\) є відрижка, існує\(x \in A\) таке, що

\[f(x) = y.\]

Тепер ці два рівняння можуть бути записані через відповідні обернені функції як

\[g^{-1}(z) = y\text[; and}\]

\[f^{-1}(y) = x.\]

Використовуючи рівняння (6.5.5) і (6.5.6), ми бачимо, що

\[\begin{array} {rcl} {f^{-1} \circ g^{-1}(z)} &= & {f^{-1}(g^{-1}(z))} \\ {} &= & {f^{-1}(y)} \\ {} &= &{x.} \end{array}\]

Використовуючи рівняння (6.5.3) і (6.5.4) знову, ми бачимо це\((g \circ f)(x) = z\). Однак з точки зору зворотної функції це означає, що

\[(g \circ f)^{-1}(z) = x.\]

Порівнюючи рівняння (6.5.7) і (6.5.8), ми показали, що для всіх\(z \in C\),\((g \circ f)^{-1}(z) = f^{-1} \circ g^{-1}(z)\). Це доводить це\((g \circ f)^{-1} = f^{-1} \circ g^{-1}\).

Вправа 6.5

1. Нехай\(A = \{1, 2, 3\}\) і\(B = \{a, b, c\}\).
   (a) Побудувати приклад функції\(f: A \to B\), яка не є біекцією. Запишіть обернену цю функцію як набір впорядкованих пар. Чи є\(f\) оберненою функцією? Поясніть. Якщо так, намалюйте діаграму зі стрілками для\(f\) і\(f^{-1}\).
   (b) Побудувати приклад функції\(g: A \to B\), яка є біекцією. Запишіть обернену цю функцію як набір впорядкованих пар. Чи є\(g\) оберненою функцією? Поясніть. Якщо так, намалюйте діаграму зі стрілками для\(g\) і\(g^{-1}\).
2. Нехай\(S = \{a, b, c, d\}\). Визначте\(f\),\(f: S \to S\) визначаючи наступний набір впорядкованих пар.
   \[f = \{(a, c), (b, b), (c, d), (d, a)\}\]
   (a) Намалюйте діаграму зі стрілками для представлення функції\(f\). Чи є функція fa bijection?
   (b) Запишіть обернене\(f\) як набір впорядкованих пар. Це\(f^{-1}\) функція? Поясніть.
   (c) Намалюйте діаграму зі стрілками для\(f^{-1}\) використання діаграми зі стрілками з вправи (2a).
   (d) Обчислити\((f^{-1} \circ f)(x)\) і\((f \circ f^{-1}(x)\) для кожного\(x\) в\(S\). Яку теорему це ілюструє?
3. Зворотні функції можуть бути використані для вирішення певних рівнянь. Ідея полягає в тому, щоб використовувати обернену функцію для скасування функції.
   (a) Оскільки функція кореня куба та функція кубінгу обертаються один від одного, ми часто можемо використовувати функцію кореня куба, щоб допомогти вирішити рівняння за участю куба. Наприклад, основним кроком у вирішенні рівняння
   \[(2t - 1)^3 = 20\]
   є прийняття кубового кореня кожної сторони рівняння. Це дає
   \[\begin{array} {rcl} {\sqrt[3]{(2t - 1)^3} &= & {\sqrt[3]{20}} \\ {2t - 1} &= &{\sqrt[3]{20}.} \end{array}\]
   Пояснити, як цей крок у вирішенні рівняння є використанням Слідство 6.28.
   
   (б) Основним кроком у розв'язанні рівняння\ (e^ {2t - 1} = 20} є прийняття натурального логарифма обох сторін цього рівняння. Поясніть, як цей крок є використанням Слідство 6.28, а потім вирішіть отримане рівняння для отримання розв'язку для t в терміні натуральної функції логарифма.
   (c) Наскільки схожі методи розв'язання рівнянь у Вправі (3а) та Вправи (3b)?
4. Доведіть частину (2) слідства 6.28. Дозволяти\(A\) і\(B\) бути непорожніми множинами і нехай\(f: A \to B\) бути bijection. Тоді для кожного\(y\) в\(B\),\((f \circ f^{-1} (y) = y\).
5. У Progress Check 6.6 на сторінці 298 ми визначили функцію ідентичності на множині. Функція ідентичності на множині\(T\), позначається\(I_T\), є функцією,\(I_T: T \to T\) визначеною\(I_T(t) = t\) для кожного\(t\) in\(T\). Поясніть, як слідство 6.28 можна констатувати, використовуючи поняття рівності функцій і функцій ідентичності на множині\(A\) і\(B\).
6. Нехай\(f: A \to B\) і\(g: B \to A\). \(I_A\)\(I_B\)Дозволяти і бути функції ідентичності на множині\(A\) і\(B\), відповідно. Доведіть кожне з наступного:
   (а) Якщо\(g \circ f = I_A\), то\(f\) це ін'єкція.
   (б) Якщо\(g \circ g = I_B\), то\(f\) є відсмоктуванням.
   (c) Якщо\(g \circ f = I_A\) і\(g \circ g = I_B\), то\(f\) і\(g\) є біекціями і\(g = f^{-1}\).
7. (а) Визначте\(f: \mathbb{R} \to \mathbb{R}\) за\(f(x) = e^{-x^2}\). Чи є\(f\) оберненою функцією? Обгрунтуйте свій висновок.
   (б) Нехай\(\mathbb{R}^{\ast} = \{x \in \mathbb{R}\ |\ x \ge 0\}\). Визначте\(g: \mathbb{R}^{\ast} \to (0,1]\) по\(g(x) = e^{-x^2}\). Чи є\(g\) оберненою функцією? Обгрунтуйте свій висновок.
8. (а)\(f: \mathbb{R} \to \mathbb{R}\) Дозволяти визначатися\(f(x) = x^2\). Поясніть, чому\(f\) обернене не є функцією.
   (б) Нехай\(\mathbb{R}^{\ast} = \{t \in \mathbb{R}\ |\ t \ge 0\}\). Визначте\(g: \mathbb{R}^{\ast} \to \mathbb{R}^{\ast}\) по\(g(x) = x^2\). Поясніть, чому ця функція квадратування (з обмеженим доменом і кодоменом) є біекцією.
   (c) Поясніть, як визначити функцію квадратного кореня як обернену функцію у Вправі (8b).
   (г) Правда чи брехня:\((\sqrt{x})^2 = x\) для всіх\(x \in \mathbb{R}\) таких, що\(x \ge 0\).
   (e) Правда чи брехня:\(\sqrt{x^2} = x\) для всіх\(x \in \mathbb{R}\).
9. Доведіть наступне:
   Якщо\(f: A \to B\) це біекція, то\(f^{-1}: B \to A\) це також біекція.
10. Для кожного натурального числа\(k\), нехай\(A_k\) бути безліч, і для кожного натурального числа\(n\), нехай\(f_n: A_n \to A_{n + 1}\).
    Наприклад,\(f_1 = A_1 \to A_2\),\(f_1 = A_1 \to A_2\),\(f_2 = A_2 \to A_3\)\(f_3 = A_3 \to A_4\), і так далі.
    Використовуйте математичну індукцію, щоб довести, що для кожного натурального числа\(n\) з\(n \ge 2\)\(f_1\), якщо\(f_2\),,...,\(f_n\) всі двоєкторії, то\(f_n \circ f_{n - 1} \circ \cdot\cdot\cdot \circ f_2 \circ f_1\) це біекція і
    \ [(f_n\ circ f_ {n - 1}\ circ\ cdot\ cdot\ cdot\ cdot\ circ f_2\ circ f_1) ^ {-1} = f_ {1} ^ {-1}\ cdot f_ {2} ^ {-1}\ cdot\ cdot\ cdot\ cdot\ cdot\ cdot\ circ f_ {n - 1} ^ {-1} ^ {-1}
    Примітка: Це розширення теореми 6.29. Насправді, Теорема 6.29 є базовим кроком цього доказу для\(n = 2\).
11. \(a) Define \(f: \mathbb{R} \to \mathbb{R}\)по\(f(x) = x^2 - 4\) для всіх\(x \in \mathbb{R}\). Поясніть, чому обернена функція не\(f\) є функцією.
    (б) Нехай\(\mathbb{R}^{\ast} = \{x \in \mathbb{R}\ |\ x \ge 0\}\) і нехай\(T = \{y \in \mathbb{R}\ |\ y \ge -4\}\). \(F: \mathbb{R}^{\ast} \to T\)Визначте\(F(x) = x^2 - 4\) для всіх\(x \in \mathbb{R}^{\ast}\). Поясніть, чому обернена функція\(F\) є функцією і знайдіть формулу для\(F^{-1}(y)\), де\(y \in T\).
12. Нехай\(\mathbb{Z}_5 = \{0, 1, 2, 3, 4\}\).
    (а) Визначте\(f: \mathbb{Z}_5 \to \mathbb{Z}_5\) по\(f(x) = x^2 + 4\) (мод 5) для всіх\(x \in \mathbb{Z}_5\). Запишіть обернену\(f\) як набір впорядкованих пар і поясніть, чому не\(f^{-1}\) є функцією.
    (б) Визначте\(g: \mathbb{Z}_5 \to \mathbb{Z}_5\) по\(g(x) = x^3 + 4\) (мод 5) для всіх\(x \in \mathbb{Z}_5\). Запишіть обернену\(g\) як набір впорядкованих пар і поясніть, чому не\(g^{-1}\) є функцією.
    (в) Чи можна написати формулу для\(g^{-1}(y)\), де\(y \in \mathbb{Z}_5\)? Відповідь на це питання залежить від того, чи можна визначити кубовий корінь елементів\(\mathbb{Z}_5\). Нагадаємо, що для дійсного числа\(x\) ми визначаємо кубічний корінь x до дійсного числа\(y\) таким, що\(y^3 = x\). Тобто,
    \[y = \sqrt[3]{x} \text{ if and only if } y^3 = x.\]
    Використовуючи цю ідею, чи можна визначити кубовий корінь кожного числа в\(\mathbb{Z}_5\)? Якщо так, то що таке\(\sqrt[3]{0}\),\(\sqrt[3]{1}\),\(\sqrt[3]{2}\),\(\sqrt[3]{3}\), і\(\sqrt[3]{4}\).
    (d) Тепер дайте відповідь на питання, поставлене на початку частини (c). Якщо є можливість, визначте формулу\(g^{-1}(y)\) де\(g^{-1}: \mathbb{Z}_5 \to \mathbb{Z}_5\).
    
    Дослідження та діяльність
13. Побудова оберненої функції. Якщо\(f: A \to B\) це біекція, то ми знаємо, що його зворотна функція. Якщо нам задано формулу для функції\(f\), то може бути бажаним визначити формулу для функції\(f^{-1}\). Це іноді можна зробити, в той час як в інший час це дуже складно або навіть неможливо.
    Дозвольте\(f: \mathbb{R} \to \mathbb{R}\) визначитися з\(f(x) = 2x^3 - 7\). Графік цієї функції може припустити, що ця функція є біекцією.
    
    (а) Доведіть, що функція f - це ін'єкція та відсмоктування.
    
    Нехай\(y \in \mathbb{R}\). Один із способів довести, що\(f\) це surjection - встановити\(y = f(x)\) та вирішити для\(x\). Якщо це можна зробити, то ми б знали, що існує\(x \in \mathbb{R}\) таке, що\(f(x) = y\). Для функції\(f\) ми використовуємо\(x\) для входу і y для виведення. Вирішуючи\(x\) for з термінами\(y\), ми намагаємося написати формулу, де\(y\) є\(x\) вхідним і є виходом. Ця формула представляє обернену функцію.
    
    (б) Розв'яжіть рівняння\(y = 2x^3 - 7\) для\(x\). Скористайтеся цим, щоб написати формулу для\(f^{-1}(y)\), де\(f^{-1}: \mathbb{R} \to \mathbb{R}\).
    (c) Використовуйте результат частини (13b), щоб перевірити, що для кожного\(x \in \mathbb{R}\),\(f^{-1}(f(x)) = x\) і для кожного\(y \in \mathbb{R}\),\(f(f^{-1}(y)) = y\).
    
    Тепер давайте\(\mathbb{R}^{+} = \{y \in \mathbb{R}\ |\ y > 0\}\). Визначте\(g: \mathbb{R} \to \mathbb{R}^{+}\) по\(g(x) = e^{2x - 1}\).
    
    (d) Встановити\(y = e^{2x - 1}\) і вирішити для з\(x\) точки зору\(y\).
    (e) Використовуйте свою роботу у Вправи (13d), щоб визначити функцію\(h: \mathbb{R}^{+} \to \mathbb{R}\).
    (f) Для кожного\(x \in \mathbb{R}\) визначте\((h \circ g)(x)\) і для кожного\(y \in \mathbb{R}^{+}\) визначте\((g \circ h)(y)\).
    (g) Використовуйте вправу (6), щоб пояснити, чому\(h = g^{-1}\).
14. Функція зворотного синуса. Ми бачили, що для того, щоб отримати обернену функцію, іноді необхідно обмежити домен (або кодомен) функції.
    
    (а)\(f: \mathbb{R} \to \mathbb{R}\) Дозволяти визначатися\(f(x) = sin x\). Поясніть, чому обернена функція не\(f\) є функцією. (Графік може бути корисним.)
    
    Зверніть увагу, що якщо ми використовуємо впорядковане парне подання, то функція синуса може бути представлена як
    \[f = \{(x, y) \in \mathbb{R} \to \mathbb{R}\ |\ y = sin x\}.\]
    Якщо ми позначимо зворотну синусоїдальної функції sin\(^{-1}\), то
    \[f^{-1} = \{(y, x) \in \mathbb{R} \to \mathbb{R}\ |\ y = sin x\}.\]
    
    Частина (14a) доводить, що\(f^{-1}\) це не функція. Однак на попередніх курсах математики ми часто використовували «функцію зворотного синуса». Це насправді не зворотна функція синуса, визначена в частині (14a), але, скоріше, це зворотна функція синуса, обмежена доменом\([-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\).
    
    (b) Поясніть, чому функція,\(F: [-\dfrac{\pi}{2}, \dfrac{\pi}{2}] \to [-1, 1]\) визначена\(F(x) = sin x\), є біекцією.
    
    Обернена функція в Part (14b) сама по собі є функцією і називається зворотною синусоїдною функцією (або іноді функцією арксина).
    
    (c) Яка область функції зворотного синуса? Що таке діапазон і кодомен функції зворотного синуса?
    
    Давайте тепер використаємо\(F(x) = \text{sin(\(x\))}\) для представлення функції обмеженого синуса в Part (14b). Отже,\(F^{-1} (x) = \text{sin\(^{-1}\) (\(x\))}\) можна використовувати для представлення функції зворотного синуса. Зауважте, що
    \[F: [-\dfrac{\pi}{2}, \dfrac{\pi}{2}] \to [-1, 1] \text{ and } F^{-1}: [-1, 1] \to [-\dfrac{\pi}{2}, \dfrac{\pi}{2}].\]
    (d) Використовуючи це позначення, поясніть, чому
    \(\text{sin\(^{-1}\)} y = x\) тоді і тільки тоді, коли [\(y = \text{sin \(x\)}\) і\(-\dfrac{\pi}{2} \le x \le \dfrac{\pi}{2}\)];
    \(\text{sin(sin\(^{-1}\)} (y)) = y\) для всіх\(y \in [-1, 1]\); і
    \(\text{sin\(^{-1}\) (sin ( \(x\)))} = х\) для всіх\(x \in [-\dfrac{\pi}{2}, \dfrac{\pi}{2}].\)

Відповідь

Додайте сюди тексти. Не видаляйте цей текст спочатку.