8.3: Графічні лінійні рівняння

Розглянемо$y = x + 1$ рівняння в двох змінних. Якщо підставити$(x, y) = (1, 2)$ впорядковану пару в рівняння$y = x + 1$, тобто, якщо замінити x на 1 і y на 2, то отримаємо істинний оператор.

$$\begin{aligned} y = x + 1 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 2=1+1 ~ & \textcolor{red}{ \text{ Substitute: 1 for } x \text{ and 2 for } y.} \\ 2=2 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber$$

Ми говоримо, що впорядкована пара (1, 2) - це рішення рівняння$y = x + 1$.

Розв'язок рівняння у двох змінних

Якщо підстановка впорядкованої пари (x, y) =( a, b) у рівняння (замінити x на a і y на b) дає істинний твердження, то впорядкована пара (a, b) називається рішенням рівняння і, як кажуть, «задовольняє рівняння».

Приклад 1

Які з впорядкованих пар є розв'язками рівняння$y = 2x + 5$: (a) (−3, −2), або (b) (5, 15)?

Рішення

Підставте точки в рівняння, щоб визначити, які є розв'язками.

а) Щоб визначити, чи є (−3, −2) розв'язком$y = 2x + 5$, замініть −3 на x та −2 для y у рівнянні$y = 2x + 5$.

$$\begin{aligned} y = 2x + 5 ~ & \textcolor{red}{ \text{ Original equation.}} \\ −2 = 2(−3) + 5 ~ & \textcolor{red}{ \text{ Substitute: −3 for } x \text{ and } −2 \text{ for } y.} \\ −2 = −6+5 ~ & \textcolor{red}{ \text{ Multiply first: } 2(−3) = −6} \\ −2 = −1 ~ & \textcolor{red}{ \text{ Add: } −6+5= −1.} \end{aligned}\nonumber$$

Оскільки отриманий оператор є помилковим, впорядкована пара (−3, −2) не задовольняє рівнянню. Впорядкована пара (−3, −2) не є розв'язком$y = 2x + 5$.

а) Щоб визначити, чи є (5, 15) розв'язком$y = 2x + 5$, підставити 5 на x і 15 для y в рівнянні$y = 2x + 5$.

$$\begin{aligned} y = 2x + 5 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 15 = 2(5) + 5 ~ & \textcolor{red}{ \text{ Substitute: 5 for } x \text{ and } 15 \text{ for } y.} \\ 15 = 10 + 5 ~ & \textcolor{red}{ \text{ Multiply first: } 2(5) = 10} \\ 15 = 15 ~ & \textcolor{red}{ \text{ Add: } 10 + 5 = 15.} \end{aligned}\nonumber$$

Отримане твердження вірно. Впорядкована пара (5, 15) задовольняє рівнянню. Отже, (5, 15) є рішенням$y = 2x + 5$.

Вправа

Які з впорядкованих пар (1, 7) і (2, 9) є розв'язком рівняння$y = 3x + 4$?

Відповідь

(1, 7)

Графік рівняння

Звертаємо свою увагу на графік рівняння.

Графік рівняння

Графік рівняння - це множина всіх впорядкованих пар, які є розв'язками рівняння.

У$y = 2x + 5$ рівнянні змінна y залежить від значення змінної x. З цієї причини ми називаємо y залежною змінною і x незалежною змінною. Ми вільні робити вибір для x, але значення y буде залежати від нашого вибору для x.

Ми також присвоїмо горизонтальну вісь незалежної змінної x, а вертикальну вісь - залежної змінної y (див. Рис. 8.7).

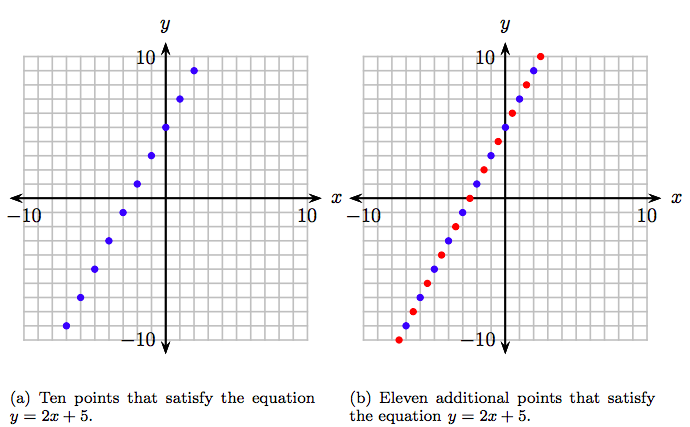
Графік$y = 2x+5$ складається з усіх впорядкованих пар, які є розв'язками рівняння$y = 2x+ 5$. Отже, наше перше завдання - знайти впорядковані пари, які є розв'язками$y = 2x + 5$. Це легко досягти, вибравши довільну кількість значень, підставивши їх на x у рівнянні$y = 2x + 5$, а потім обчисливши отримані значення y. З огляду на цю думку, ми вибираємо довільні цілі числа −7, −6,., 2, підставляємо їх на x у рівнянні$y = 2x + 5$, обчислити отримане значення y, і зберегти результати в таблиці.

$$\begin{array}{|r|r|r|r|} \hline y = 2x+5 & x & y & (x,~y) \\ \hline y = 2(−7) + 5 = −9 & −7 & −9 & (−7, −9) \\ y = 2(−6) + 5 = −7 & −6 & −7 & (−6, −7) \\ y = 2(−5) + 5 = −5 & −5 & −5 & (−5, −5) \\ y = 2(−4) + 5 = −3 & −4 & −3 & (−4, −3) \\ y = 2(−3) + 5 = −1 & −3 & −1 & (−3, −1) \\ y = 2(−2) + 5 = 1 & −2 & 1 & (−2, 1) \\ y = 2(−1) + 5 = 3 & −1 & 3 & (−1, 3) \\ y = 2(0) + 5 = 5 & 0 & 5 & (0, 5) \\ y = 2(1) + 5 = 7 & 1 & 7 & (1, 7) \\ y = 2(2) + 5 = 9 & 2 & 9 & (2, 9) \\ \hline \end{array}\nonumber$$

В результаті виходить 10 впорядкованих пар, які задовольняють рівнянню$y = 2x + 5$. Тому ми маємо 10 впорядкованих пар, які належать до графіку$y = 2x + 5$. Вони нанесені на малюнку 8.7 (а).

Однак ми ще не закінчили, тому що графік рівняння$y = 2x + 5$ - це набір всіх точок, які задовольняють рівнянню, і ми тільки побудували 10 таких точок. Давайте намітимо ще кілька моментів. Виберіть ще кілька значень x, обчислите відповідне значення y та запишіть результати в таблицю.

$$\begin{array}{|r|r|r|r|} \hline y = 2x + 5 & x & y & (x, y) \\ \hline y = 2(−7.5) + 5 = −10 & −7.5 & −10 & (−7.5, −10) \\ y = 2(−6.5) + 5 = −8 & −6.5 & −8 & (−6.5, −8) \\ y = 2(−5.5) + 5 = −6 & −5.5 & −6 & (−5.5, −6) \\ y = 2(−4.5) + 5 = −4 & −4.5 & −4 & (−4.5, −4) \\ y = 2(−3.5) + 5 = −2 & −3.5 & −2 & (−3.5, −2) \\ y = 2(−2.5) + 5 = 0 & −2.5 & 0 & (−2.5, 0) \\ y = 2(−1.5) + 5 = 2 & −1.5 & 2 & (−1.5, 2) \\ y = 2(−0.5) + 5 = 4 & −0.5 & 4 & (−0.5, 4) \\ y = 2(0.5) + 5 = 6 & 0.5 & 6 & (0.5, 6) \\ y = 2(1.5) + 5 = 8 & 1.5 & 8 & (1.5, 8) \\ y = 2(2.5) + 5 = 10 & 2.5 & 10 & (2.5, 10) \\ \hline \end{array}\nonumber$$

Це 11 додаткових точок, які ми додаємо до графіка на малюнку 8.7 (b).

Малюнок 8.7: Побудова точок, що задовольняють рівнянню$y = 2x + 5$.

Зверніть увагу, що ми можемо продовжувати нескінченно довго таким чином, додаючи точки в таблицю і будуючи їх. Однак рано чи пізно нам доведеться зробити стрибок віри і уявити, як буде виглядати остаточний графік, коли всі точки, які задовольняють рівнянню y = 2x+ 5, побудовані. Ми робимо це на малюнку 8.8, де підсумковий графік набуває вигляду прямої.

Використання лінійки

Всі лінії необхідно провести за допомогою лінійки. Сюди входять осі x - і y.

Важливе спостереження. Коли ми використовуємо лінійку, щоб провести лінію через нанесені точки на малюнку 8.7 (b), доходячи до кінцевого результату на малюнку 8.8, ми повинні розуміти, що це техніка ярлика для побудови всіх інших впорядкованих пар, які задовольняють рівнянню. Ми насправді не малюємо лінію через намальовані точки. Швидше, ми затінюємо всі впорядковані пари, які задовольняють рівняння$y = 2x + 5$.

Малюнок 8.8: Графік рівняння$y = 2x + 5$.

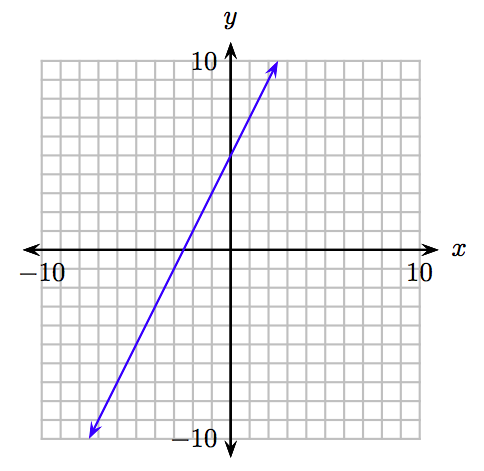
Результат. Графік рівняння$y = 2x + 5$, зображений на малюнку 8.8, являє собою лінію. Насправді, графік - це нескінченна сукупність точок$y = 2x + 5$, що задовольняють рівняння, яке приймає форму прямої, але це все в порядку сказати, що графік$y = 2x + 5$ є лінією.

Впорядковані пари та графік

Оскільки графік рівняння є сукупністю всіх впорядкованих пар, які задовольняють рівнянню, ми маємо два важливих результату:

1. Якщо впорядкована пара задовольняє рівнянню, то точка в декартовій площині, представлена впорядкованою парою, знаходиться на графіку рівняння.
2. Якщо точка знаходиться на графіку рівняння, то впорядковане парне подання цієї точки задовольняє рівнянню.

Приклад 2

Знайти значення k так, щоб точка (2, k) виявилася на графіку рівняння$y = 3x − 2$.

Рішення

Якщо точка (2, k) знаходиться на графіку$y = 3x−2$, то вона повинна задовольняти рівнянню$y = 3x − 2$.

$$\begin{aligned} y = 3x − 2 ~ & \textcolor{red}{ \text{ Original equation.}} \\ k = 3(2) − 2 ~ & \begin{array}{l} \textcolor{red}{ \text{ The point (2, } k) \text{ is on the graph.}} \\ \textcolor{red}{ \text{ Substitute 2 for } x \text{ and } k \text{ for } y \text{ in } y = 3x − 2.} \end{array} \\ k = 6 − 2 ~ & \textcolor{red}{ \text{ Multiply: } 3(2) = 6.} \\ k = 4 ~ & \textcolor{red}{ \text{ Subtract: } 6 − 2 = 4.} \end{aligned}\nonumber$$

Таким чином, k = 4.

Вправа

Знайти значення k так, щоб точка (k, −3) була на графіку рівняння$y = 4x + 2$.

Відповідь

k = −5/4

Лінійні рівняння

Давайте побудуємо графік іншого рівняння.

Приклад 3

Намалюйте графік$y = −2x + 1$.

Рішення

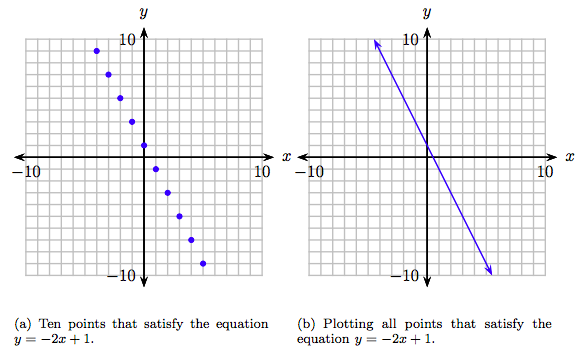
Виберіть довільні значення x: −4, −3,., 5. Підставте ці значення в рівняння$y = −2x + 1$, обчисліть отримане значення y, а потім розташуйте свої результати в таблиці.

$$\begin{array}{|r|r|r|r|} \hline y = −2x + 1 & x & y & (x, y) \\ \hline y = −2(−4) + 1 = 9 & −4 & 9 & (−4, 9) \\ y = −2(−3) + 1 = 7 & −3 & 7 & (−3, 7) \\ y = −2(−2) + 1 = 5 & −2 & 5 & (−2, 5) \\ y = −2(−1) + 1 = 3 & −1 & 3 & (−1, 3) \\ y = −2(0) + 1 = 1 & 0 & 1 & (0, 1) \\ y = −2(1) + 1 = −1 & 1 & −1 & (1, −1) \\ y = −2(2) + 1 = −3 & 2 & −3 & (2, −3) \\ y = −2(3) + 1 = −5 & 3 & −5 & (3, −5) \\ y = −2(4) + 1 = −7 & 4 & −7 & (4, −7) \\ y = −2(5) + 1 = −9 & 5 & −9 & (5, −9) \\ \hline \end{array}\nonumber$$

Ми намалювали точки в таблиці на малюнку 8.9 (a). На малюнку 8.9 (a) є достатньо доказів, щоб уявити, що якби ми побудували всі точки, які задовольняли рівнянню$y = −2x + 1$, результатом буде лінія, показана на малюнку 8.9 (b).

Малюнок 8.9: Графік рівняння$y = −2x + 1$ є лінією.

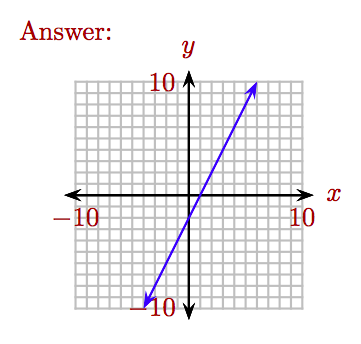
Вправа

Намалюйте графік$y = 2x − 2$.

Відповідь

Графік на$y = 2x + 5$ малюнку 8.8 є лінією. Графік на$y = −2x + 1$ малюнку 8.9 (б) також є лінією. Це призведе до підозри, що графік рівняння$y = mx+b$, де m і b є константами, завжди буде лінією. Дійсно, це завжди так.

Лінійні рівняння

Графік$y = mx + b$, де m і b - константи, завжди буде рядком. З цієї причини рівняння$y = mx+b$ називається лінійним рівнянням.

Приклад 4

Яке з наведених нижче рівнянь є лінійним рівнянням? 1. $y = −3x + 4$, 2. $y = \frac{2}{3}x + 3$, і 3. $y = 2x^2 + 4$.

Рішення

Порівняйте кожне рівняння із загальною формою лінійного рівняння,$y = mx + b$.

1. Зверніть увагу, що$y = −3x + 4$ має вигляд$y = mx + b$, де m = −3 і b = 4. Значить,$y = −3x + 4$ є лінійним рівнянням. Його графік - це лінія.
2. Зверніть увагу, що$y = \frac{2}{3} x+ 3$ має вигляд$y = mx+b$, де m = 2/3 і b = 3. Значить,$y = \frac{2}{3} x + 3$ є лінійним рівнянням. Його графік - це лінія.
3. Рівняння$y = 2x^2 + 4$ не має вигляду$y = mx + b$. Показник 2 на x перешкоджає цьому рівнянню бути лінійним. Це нелінійне рівняння. Його графік не є лінією.

Вправа

Яке з наведених нижче рівнянь є лінійним рівнянням? а)$y = 2x^3 + 5$ б)$y= -3x-5$

Відповідь

$y = −3x − 5$

Той факт, що$y = mx + b$ є лінійним рівнянням, дозволяє нам швидко накидати його графік.

Приклад 5

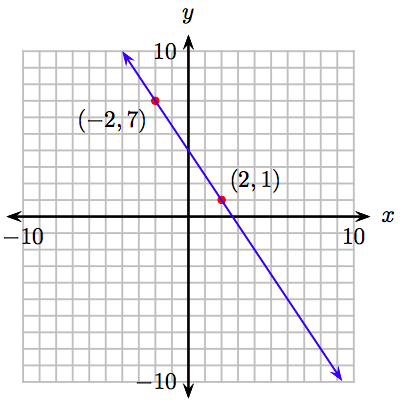
Намалюйте графік$y = − \frac{3}{2} x + 4$.

Рішення

Рівняння$y = −3 2x+ 4$ має вигляд$y = mx+b$. Тому рівняння лінійне, а графік буде лінією. Оскільки дві точки визначають лінію, нам потрібно знайти лише дві точки, які задовольняють рівнянню$y = − \frac{3}{2} x + 4$, побудувати їх, а потім провести лінію через них лінійкою. Вибираємо x = −2 і x = 2, обчислюємо y і записуємо результати в таблицю.

$$\begin{array}{|r|r|r|r|} \hline y = − \frac{3}{2} x + 4 & x & y & (x, y) \\ \hline y = − \frac{3}{2} (−2) + 4 = 3 + 4 = 7 & −2 & 7 & (−2, 7) \\ y = − \frac{3}{2} (2) + 4 = −3+4=1 & 2 & 1 & (2, 1) \\ \hline \end{array}\nonumber$$

Покладіть точки (−2, 7) і (2, 1) і проведіть через них лінію. Результат показаний на малюнку 8.10.

Малюнок 8.10: Графік$y = − \frac{3}{2} x + 4$ - це лінія.

Вправа

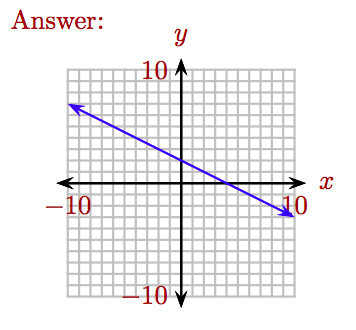
Намалюйте графік$y = − \frac{1}{2} x + 2$.

Відповідь

Можливо, ви зазначали у прикладі 5, які є варіантами −2 та 2 для x полегшили обчислення відповідних y -значень через результат скасування.

Вибір стратегічних цінностей

При побудові лінійного рівняння хороша стратегія вибору значень x, які спрощують обчислення відповідних y -значень.

Приклад 6

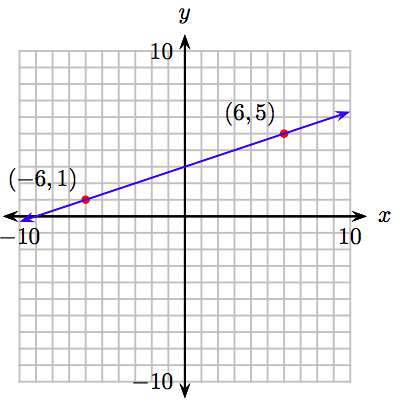
Намалюйте графік y =\ frac {1} {3} x + 3.

Рішення

Рівняння$y = \frac{1}{3} x + 3$ має вигляд$y = mx + b$. Тому рівняння лінійне, а графік буде лінією. Оскільки дві точки визначають лінію, нам потрібно знайти лише дві точки, які задовольняють рівнянню y = 1 3x + 3, побудувати їх, а потім провести лінію через них лінійкою. Ми вибираємо x = −6 і x = 6, обчислюємо y і записуємо результати в таблицю.

$$\begin{array}{|r|r|r|r|} \hline y = \frac{1}{3} x + 3 & x & y & (x, y) \\ \hline y = \frac{1}{3} (−6) + 3 = −2+3=1 & −6 & 1 & (−6, 1) \\ y = \frac{1}{3} (6) + 3 = 2 + 3 = 5 & 6 & 5 & (6, 5) \\ \hline \end{array}\nonumber$$

Покладіть точки (−6, 1) і (6, 5) і проведіть через них лінію. Результат показаний на малюнку 8.11.

Малюнок 8.11: Графік$y = \frac{1}{3}x + 3$ - це лінія.

Вправа

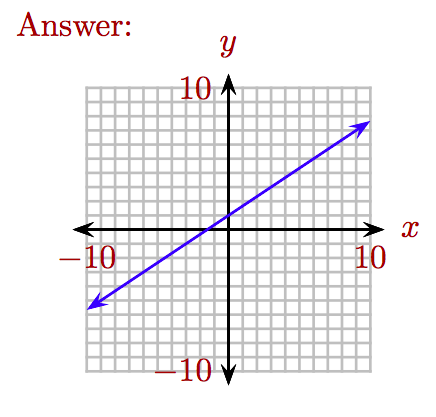
Намалюйте графік$y = \frac{2}{3} x + 1$.

Відповідь

Вправи

1. Яка з точок (2, −14), (−1, −6), (−8, 11) та (3, −13) є розв'язком рівняння$y = −2x − 8$?

2. Яка з точок (1, −2), (8, 23), (−3, −23) та (8, 24) є розв'язком рівняння$y = 4x − 9$?

3. Яка з точок (1, −1), (−2, 20), (−4, 31) та (−9, 64) є розв'язком рівняння$y = −6x + 7$?

4. Яка з точок (−8, −61), (4, 42), (−3, −18) та (−6, −46) є розв'язком рівняння$y = 9x + 8$?

5. Яка з точок (2, 15), (−8, −74), (2, 18) та (5, 40) є розв'язком рівняння$y = 9x − 3$?

6. Яка з точок (−9, −52), (−8, −44), (−7, −37) та (8, 35) є розв'язком рівняння$y = 5x − 5$?

7. Яка з точок (−2, 12), (−1, 12), (3, −10) та (−2, 14) є розв'язком рівняння$y = −5x + 4$?

8. Яка з точок (6, 25), (−8, −14), (8, 33) та (−7, −9) є розв'язком рівняння$y = 3x + 9$?

---

9. Визначте k так, щоб точка (9, k) була розв'язком$y = −6x + 1$.

10. Визначте k так, щоб точка (−9, k) була розв'язком$y = 2x + 3$.

11. Визначте k так, щоб точка (k, 7) була розв'язком$y = −4x + 1$.

12. Визначте k так, щоб точка (k, −4) була розв'язком$y = 8x + 3$.

13. Визначте k так, щоб точка (k, 1) була розв'язком$y = 4x + 8$.

14. Визначте k так, щоб точка (k, −7) була розв'язком$y = −7x + 5$.

15. Визначте k так, щоб точка (−1, k) була розв'язком$y = −5x + 3$.

16. Визначте k так, щоб точка (−3, k) була розв'язком$y = 3x + 3$.

---

У вправах 17-24, яке з заданих рівнянь є лінійним рівнянням?

17. $y = 6x^2 + 4, ~ y = x^2 + 6x + 4, ~ y = 6x + 4, ~ y = \sqrt{6x + 4}$

18. $y = −2x + 1, ~ y = x^2 − 2x + 1, ~ y = \sqrt{−2x + 1}, ~ y = −2x^2 + 1$

19. $y = x + 7, ~ y = \sqrt{x + 7}, ~ y = x^2 + 7, ~ y = x^2 + x + 7$

20. $y = x^2 + 5x + 1, ~ y = 5x^2 + 1, ~ y = \sqrt{5x + 1}, ~ y = 5x + 1$

21. $y = x^2 − 2x − 2, ~ y = −2x^2 − 2, ~ y = \sqrt{−2x − 2}, ~ y = −2x − 2$

22. $y = x^2 + 5x − 8, ~ y = 5x^2 − 8, ~ y = \sqrt{5x − 8}, ~ y = 5x − 8$

23. $y = x^2 + 7x − 3, ~ y = 7x^2 − 3, ~ y = 7x − 3, ~ y = \sqrt{7x − 3}$

24. $y = \sqrt{−4x − 3}, ~ y = x^2 − 4x − 3, ~ y = −4x − 3, ~ y = −4x^2 − 3$

---

У вправах 25-28, яке з заданих рівнянь має заданий графік?

25. $y = − \frac{3}{2}x + 2, ~ y = \frac{3}{2} x − 3, ~ y = −3x + 1, ~ y = −2x + 1$

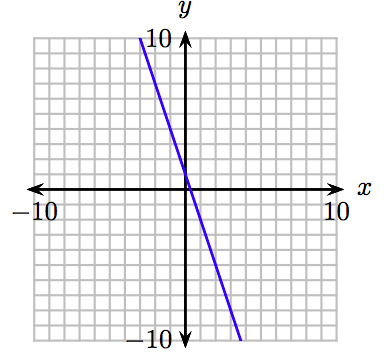
26. $y = −3x − 2, ~ y = \frac{3}{2} x + 1, ~ y = −2x − 1, ~ y = \frac{5}{2}x +$2

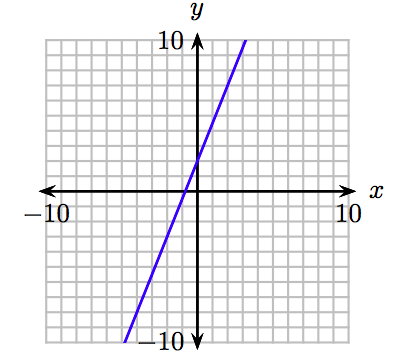
27. $y = \frac{5}{2} x − 2, ~ y = 3x + 3, ~ y = \frac{3}{2} x + 1, ~ y = \frac{1}{2} x + 1$

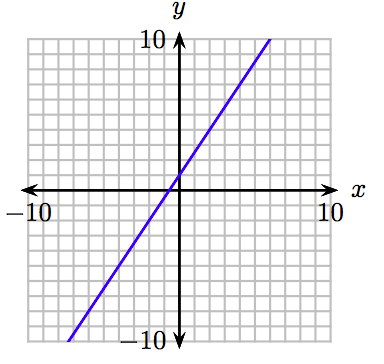
28. $y = 3x + 1, ~ y = \frac{5}{2} x − 1, ~ y = − \frac{5}{2} x − 3, ~ y = \frac{3}{2} x − 2$

---

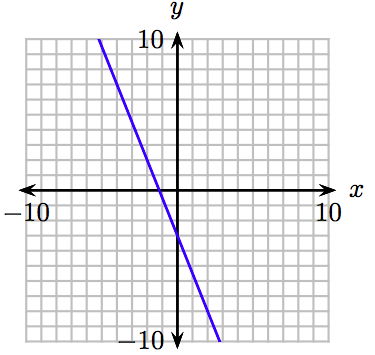
29. $y = 3x − 2$

30. $y = \frac{5}{2}x + 1$

31. $y = −2x − 1$

32. $y = \frac{5}{2} x + 2$

33. $y = −2x + 2$

34. $y = − \frac{5}{2}x − 2$

35. $y = −2x − 2$

36. $y = − \frac{5}{2}x + 1$

37. $y = 2x − 2$

38. $y = \frac{5}{2} x − 1$

39. $y = \frac{3}{2}x + 1$

40. $y = 2x + 2$

41. $y = 2x − 3$

42. $y = − \frac{5}{2}x − 1$

43. $y = \frac{3}{2}x + 3$

44. $y = 3x + 1$

---

45. Намалюйте лінії$y = \frac{1}{2} x−1$ і$y = \frac{5}{2} x−2$ на графічному папері. Коли ви підмітаєте очі зліва направо, яка лінія піднімається швидше?

46. Намалюйте лінії$y = \frac{5}{2} x+ 1$ і$y = 3x+ 1$ на графічному папері. Коли ви підмітаєте очі зліва направо, яка лінія піднімається швидше?

47. Намалюйте лінію$y = − \frac{1}{2} x + 1$ і$y = −3x+ 3$. Коли ви підмітаєте очі зліва направо, яка лінія падає швидше?

48. Намалюйте лінію$y = −3x − 1$ і$y = − \frac{5}{2} x−2$. Коли ви підмітаєте очі зліва направо, яка лінія падає швидше?

49. Намалюйте лінію$y = −3x − 1$ і$y = − \frac{1}{2} x−2$. Коли ви підмітаєте очі зліва направо, яка лінія падає швидше?

50. Намалюйте лінію$y = −3x − 1$ і$y = − \frac{1}{2}x+1$. Коли ви підмітаєте очі зліва направо, яка лінія падає швидше?

51. Намалюйте лінії$y = \frac{3}{2} x−2$ і$y = 3x+ 1$ на графічному папері. Коли ви підмітаєте очі зліва направо, яка лінія піднімається швидше?

52. Намалюйте лінії$y = \frac{1}{2} x+ 3$ і$y = \frac{5}{2}x+ 1$ на графічному папері. Коли ви підмітаєте очі зліва направо, яка лінія піднімається швидше?

---

Відповіді

1. (−1, −6)

3. (−4, 31)

5. (2, 15)

7. (−2, 14)

9. k = −53

11. к =$− \frac{3}{2}$

13. к =$− \frac{7}{4}$

15. к = 8

17. $y = 6x + 4$

19. $y = x + 7$

21. $y = −2x − 2$

23. $y = 7x − 3$

25. $y = −3x + 1$

27. $y = \frac{3}{2} x + 1$

29. $y = 3x − 2$

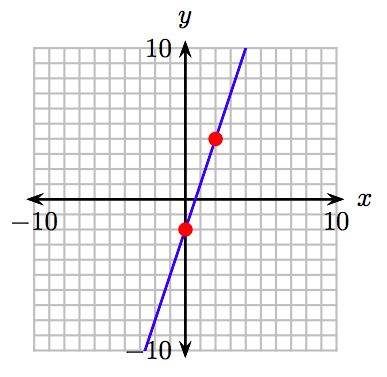
31. $y = −2x − 1$

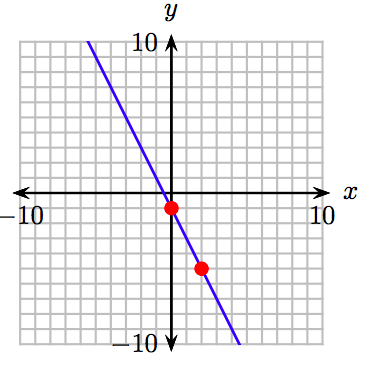
33. $y = −2x + 2$

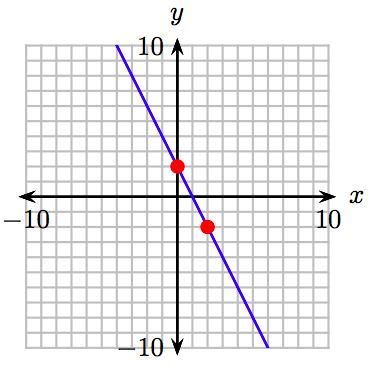
35. $y = −2x -2$

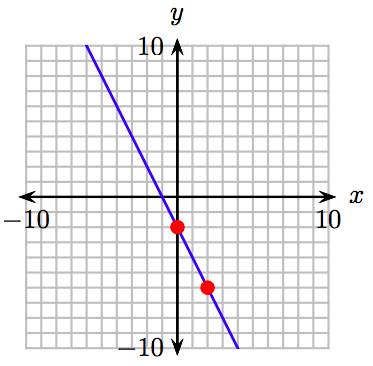
37. $y = 2x-2$

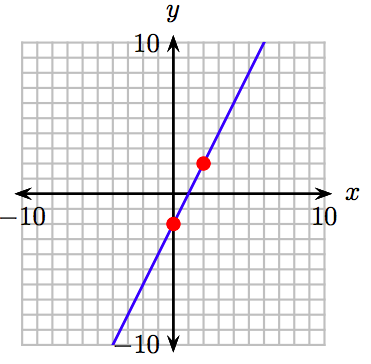
39. $y = \frac{3}{2} + 1$

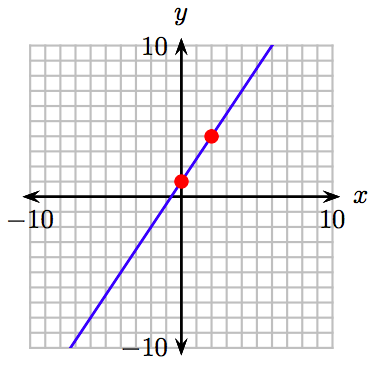
41. $y = 2x − 3$

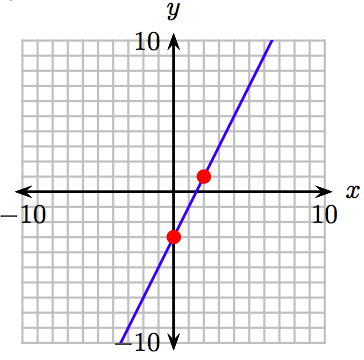
43. $y = \frac{3}{2} x + 3$

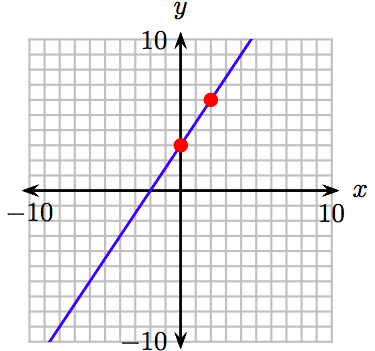
45. Графік$y = \frac{5}{2} x−2$ піднімається швидше.

47. Графік$y = −3x + 3$ падає швидше.

49. Графік$y = −3x − 1$ падає швидше.

51. Графік$y = 3x+1$ піднімається швидше.