5.7: Рівняння з десятковими числами

Last updated
Save as PDF

Page ID: 57301

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ми можемо додати або відняти одне і те ж десяткове число з обох сторін рівняння, не впливаючи на рішення.

Приклад 1

Розв'язувати для x: x − 1.35 = −2.6.

Рішення

Щоб скасувати віднімання 1,35, додайте 1,35 до обох сторін рівняння.

\[ \begin{aligned} x - 1.35 = -2.6 ~ & \textcolor{red}{ \text{ Original equation.}} \\ x - 1.35 + 1.35 = -2.6 + 1.35 ~ & \textcolor{red}{ \text{ Add 1.35 to both sides.}} \\ x = -1.25 ~ & \textcolor{red}{ \text{ Simplify: } -2.6 + 1.35 = -1.25.} \end{aligned}\nonumber \]

Вправа

Вирішити для х:$x+1.25=0.6$

Відповідь: −0,65

Ми все ще можемо помножити обидві сторони рівняння на одне і те ж десяткове число, не впливаючи на рішення.

Приклад 2

Вирішити для х:$\frac{x}{-0.35} = 4.2$.

Рішення

Щоб скасувати ділення на −0,35, помножте обидві сторони рівняння на −0,35.

\[ \begin{aligned} \frac{x}{-0.35} = 4.2 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -0.35 \left( \frac{x}{-0.35} \right) = -0.35 (4.2) ~ & \textcolor{red}{ \text{ Multiply both sides by } -0.35.} \\ x = -1.470 ~ & \textcolor{red}{ \text{ Simplify: } -0.35 (4.2) = -1.470.} \end{aligned}\nonumber \]

Вправа

Вирішити для y:$\frac{y}{0.37} = -1.52$.

Відповідь: −0.5624

Ми все ще можемо розділити обидві сторони рівняння на одне і те ж десяткове число, не впливаючи на рішення.

Приклад 3

Вирішити для х:$−1.2x = −4.08$.

Рішення

Щоб скасувати множення на −1.2, розділіть обидві сторони рівняння на −1.2.

\[ \begin{aligned} -1.2x = -4.08 ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{-1.2x}{-1.2} = \frac{-4.08}{-1.2} ~ & \textcolor{red}{ \text{ Divide both sides by } -1.2} \\ x = 3.4 ~ & \textcolor{red}{ \text{ Simplify: } -4.08/(-1.2)=3.4.} \end{aligned}\nonumber \]

Вправа

Вирішити для z:$-2.5z=1.4$

Відповідь: −0.56

Комбінування операцій

Нам іноді потрібно комбінувати операції.

Приклад 4

Вирішити для х:$−3.8x − 1.7 = −17.28$.

Рішення

Щоб скасувати віднімання 1.7, додайте 1.7 до обох сторін рівняння.

\[ \begin{aligned} -3.8x-1.7=-17.28 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -3.8x-1.7+1.7=-17.28+1.7 ~ & \textcolor{red}{ \text{ Add 1.7 to both sides.}} \\ -3.8x=-15.58 ~ & \textcolor{red}{ \text{ Simplify: } -17.28 + 1.7 = -15.58.} \end{aligned}\nonumber \]

Далі, щоб скасувати множення на −3.8, розділіть обидві сторони рівняння на −3.8.

\[ \begin{aligned} \frac{-3.8x}{-3.8} = \frac{-15.88}{-3.8} ~ & \textcolor{red}{ \text{ Divide both sides by } -3.8.} \\ x = 4.1 ~ & \textcolor{red}{ \text{ Simplify: } -15.58/(-3.8) = 4.1.} \end{aligned}\nonumber \]

Вправа

Вирішіть для вас:$-0.02u-3.2=-1.75$.

Відповідь: −72,5

Поєднання подібних термінів

Поєднання подібних термінів з десятковими коефіцієнтами здійснюється таким же чином, як комбінування подібних термінів з цілими коефіцієнтами.

Приклад 5

Спростити вираз:$−3.2x + 1.16x$.

Рішення

Щоб об'єднати ці подібні терміни, ми повинні додати коефіцієнти.

Щоб скласти коефіцієнти з несхожими знаками, спочатку відніміть коефіцієнт з меншою величиною від коефіцієнта з більшою величиною.

\[\begin{array}{r} 3.20 \\ - 1.16 \\ \hline 2.04 \end{array}\nonumber \]

Префікс знака десяткового числа, що має більшу величину. Звідси:

\[−3.2+1.16 = −2.04.\nonumber \]

Тепер ми можемо комбінувати подібні терміни наступним чином:

\[−3.2x + 1.16x = −2.04x\nonumber \]

Вправа

Спростити:$-1.185t+3.2t$

Відповідь: 2 015 т

Розв'язуючи рівняння, нам іноді потрібно поєднувати подібні терміни.

Приклад 6

Розв'яжіть рівняння для x:$4.2 − 3.1x + 2x = −7.02$.

Рішення

Поєднуйте подібні члени на лівій стороні рівняння.

\[ \begin{aligned} 4.2-3.1x+2x=-7.02 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 4.2 - 1.1x = -7.02 ~ & \textcolor{red}{ \text{ Combine like terms: } -3.1x + 2x = -1.1x.} \\ 4.2 - 1.1x - 4.2 = -7.02 - 4.2 ~ & \textcolor{red}{ \text{ Subtract 4.2 from both sides.}} \\ -1.1x = -11.02 ~ & \textcolor{red}{ \text{ Subtract: } -7.02 - 4.2 = -11.22.} \\ \frac{-1.1x}{-1.1} = \frac{-11.22}{-1.1} ~ & \textcolor{red}{ \text{ Divide both sides by } -1.1.} \\ x = 10.2 ~ & \textcolor{red}{ \text{ Divide: } -11.22/(-1.1) = 10.2.} \end{aligned}\nonumber \]

Таким чином, рішення рівняння дорівнює 10.2.

Перевірити

Як і всі рівняння, ми можемо перевірити наше рішення, підставивши нашу відповідь у вихідне рівняння.

\[ \begin{aligned} 4.2 - 3.1x +2x = -7.02 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 4.2 - 3.1(10.2) + 2(10.2) = -7.02 ~ & \textcolor{red}{ \text{ Substitute 10.2 for } x.} \\ 4.2 - 31.62 + 20.4 = -7.02 ~ & \textcolor{red}{ \text{ Multiply: } 3.1(10.2) = 31.62, ~ 2(10.2) = 20.4.} \\ -27.42 + 20.4 = -7.02 ~ & \textcolor{red}{ \text{ Order of Ops: Add, left to right.}} \\ ~ & \textcolor{red}{ ~ 4.2 - 31.62 = -27.42.} \\ -7.02 = -7.02 ~ & \textcolor{red}{ \text{ Add: } -27.42 + 20.4 = -7.02.} \end{aligned}\nonumber \]

Оскільки останній рядок є справжнім твердженням, рішення x = 10.2 перевіряє.

Вправа

Вирішити для r:$-4.2 + 3.6r - 4.1r = 1.86$

Відповідь: −12.12

Використання розподільної власності

Іноді нам потрібно буде використовувати розподільну властивість при вирішенні рівнянь.

Розподільна власність

Нехай a, b і c будуть будь-якими числами. Потім,

\[a(b + c) = ab + ac.\nonumber \]

Приклад 7

Розв'яжіть рівняння для x:$−6.3x − 0.4(x − 1.2) = −0.86$.

Рішення

Спочатку ми розподіляємо −0,4 рази кожен член у дужках, а потім об'єднаємо подібні терміни.

\[ \begin{aligned} -6.3x - 0.4(x-1.2) = -0.86 ~ & \textcolor{red}{ \text{ Original equation.}} \\ -6.3x-0.4x+0.48 = -0.86 ~ & \textcolor{red}{ \text{ Distribute. Note that } -0.4(-1.2)=0.48.} \\ -6.7x+0.48=-0.86 ~ & \textcolor{red}{ \text{ Combine like terms.}} \end{aligned}\nonumber \]

Далі відніміть 0,48 з обох сторін, потім розділіть обидві сторони отриманого рівняння на −6,7.

\[ \begin{aligned} -6.7x+0.48-0.48 = -0.86 - 0.48 ~ & \textcolor{red}{ \text{ Subtract 0.48 from both sides.}} \\ -6.7x = -1.34 ~ & \textcolor{red}{ \text{ Simplify: } -0.86 - 0.48 = -1.34.} \\ \frac{-6.7x}{-6.7} = \frac{-1.34}{-6.7} ~ & \textcolor{red}{ \text{ Divide both sides by } -6.7.} \\ x = 0.2 ~ & \textcolor{red}{ \text{ Simplify: } -1.34/(-6.7)=0.2.} \end{aligned}\nonumber \]

Вправа

Вирішити для х:$ −2.5x − 0.1(x − 2.3) = 8.03$

Відповідь: −3

Рішення округлення

Іноді приблизне рішення буває адекватним.

Приклад$\PageIndex{1}$

Розв'яжіть рівняння$3.1x+ 4.6=2.5 − 2.2x$ для x. Округляйте відповідь до найближчої десятої.

Рішення

Нам потрібно виділити члени, що містять x на одній стороні рівняння. Ми починаємо з додавання 2.2x до обох сторін рівняння.

\[ \begin{aligned} 3.1x + 4.6 = 2.5 - 2.2x ~ & \textcolor{red}{ \text{ Original equation.}} \\ 3.1x + 4.6 + 2.2x = 2.5 - 2.2x + 2.2x ~ & \textcolor{red}{ \text{ Add } 2.2x \text{ to both sides.}} \\ 5.3x + 4.6 = 2.5 ~ & \textcolor{red}{ \text{ Combine terms: } 3.1x + 2.2x = 5.3x.} \end{aligned{\nonumber \]

\[ \begin{aligned} 5.3x + 4.6 - 4.6 = 2.5 - 4.6 ~ & \textcolor{red}{ \text{ Subtract 4.6 from both sides.}} \\ 5.3x = -2.1 ~ & \textcolor{red}{ \text{ Simplify: } 2.5 - 4.6 = -2.1.} \end{aligned}\nonumber \]

Щоб скасувати ефект множення на 5.3, розділіть обидві сторони рівняння на 5,3.

\[ \begin{aligned} \frac{5.3x}{5.3} = \frac{-2.1}{5.3} ~ & \textcolor{red}{ \text{Divide both side by 5.3.}} \\ x \approx -0.4 ~ & \textcolor{red}{ \text{ Round solution to nearest tenth.}} \end{aligned}\nonumber \]

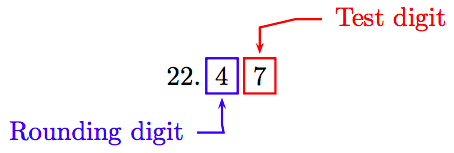
Щоб округлити відповідь до найближчої десятої, треба провести поділ на одне додаткове місце.

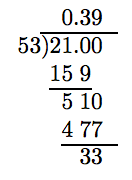
$Знімок екрана 2019-09-11 в 4.43.18 PM.png$

Оскільки «тестова цифра» більше або дорівнює 5, додайте 1 до цифри округлення і обрізайте.

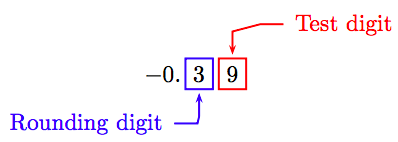
$Знімок екрана 2019-09-11 в 4.43.23 PM.png$

Таким чином, −0,39 ≈ −0,4.

Таким чином, −2.1/5.3 ≈ −0,39.

Вправа

Вирішити для х:$4.2x − 1.25 = 3.4+0.71x$

Відповідь: 1.33

Додатки

Давайте розглянемо деякі програми, які включають рівняння, що містять десяткові числа. Для зручності повторюємо Вимоги до вирішення проблем Word.

Вимоги до вирішення проблем Word

Налаштуйте словник змінних. Ви повинні повідомити своїм читачам, що представляє кожна змінна у вашій проблемі. Це може бути досягнуто кількома способами:
1. Такі заяви, як «Нехай P представляє периметр прямокутника».
2. Позначення невідомих значень змінними в таблиці.
3. Маркування невідомих величин в ескізі або схемі.
Налаштуйте рівняння. Кожне рішення проблеми зі словом має містити ретельно розроблене рівняння, яке точно описує обмеження в постановці задачі.
Розв'яжіть рівняння. Ви завжди повинні вирішувати рівняння, встановлене на попередньому кроці.
Дайте відповідь на питання. Цей крок легко не помітити. Наприклад, проблема може запитати вік Джейн, але рішення вашого рівняння дає вік сестри Джейн Ліз. Переконайтеся, що ви відповіли на оригінальне запитання, поставлене в проблемі. Ваше рішення має бути записано в реченні з відповідними одиницями.
Озирніться назад. Важливо зазначити, що цей крок не означає, що ви повинні просто перевірити своє рішення у своєму рівнянні. Зрештою, можливо, ваше рівняння неправильно моделює ситуацію задачі, тож ви можете мати правильне рішення неправильного рівняння. Важливе питання: «Чи має сенс ваша відповідь на основі слів в оригінальній постановці проблеми».

Почнемо з прямокутної садової проблеми.

Приклад 9

Моллі потрібно створити прямокутний садовий ділянку площею 200 квадратних метрів (200 м ²). Якщо ширина ділянки 8,9 метра, знайдіть довжину ділянки правильною до найближчої десятої частки метра.

Рішення

Ми будемо слідувати Вимоги до вирішення проблем Word.

1. Налаштуйте словник змінних. Ми будемо використовувати ескіз для визначення наших змінних.

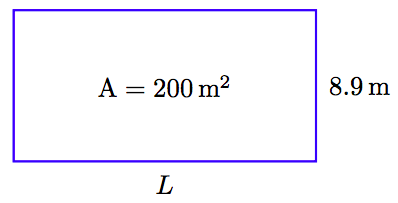
$Знімок екрана 2019-09-11 в 4.51.36 PM.png$

Зверніть увагу, що L представляє довжину прямокутника.

2. Налаштуйте рівняння. Площа A прямокутника задається за формулою

\[A = LW,\nonumber \]

де L і W представляють довжину і ширину прямокутника відповідно. Підставляємо 200 на А і 8,9 на W в формулу для отримання

\[200 = L(8.9),\nonumber \]

або еквівалентно,

\[200 = 8.9L.\nonumber \]

3. Розв'яжіть рівняння. Розділіть обидві сторони останнього рівняння на 8,9, а потім округліть відповідь до найближчої десятої.

\[ \begin{aligned} \frac{200}{8.9} = \frac{8.9L}{8.9} ~ & \textcolor{red}{ \text{ Divide both sides by 8.9.}} \\ 22.5 \approx L ~ & \textcolor{red}{ \text{ Round to nearest tenth.}} \end{aligned}\nonumber \]

Щоб округлити відповідь до найближчої десятої, треба провести поділ на одне додаткове місце.

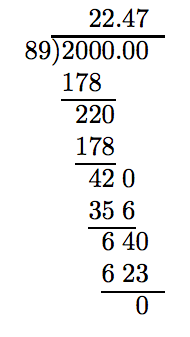
$Знімок екрана 2019-09-11 в 4.51.44 PM.png$

Оскільки «тестова цифра» більше або дорівнює 5, додайте 1 до цифри округлення і обрізайте.

$Знімок екрана 2019-09-11 в 4.51.49 PM.png$

Таким чином, 200/8.9 ≈ 22.5.

4. Дайте відповідь на питання. До найближчої десятої частки метра довжина прямокутної ділянки становить L ≈ 22,5 метра.

5. Озирніться назад. У нас L ≈ 22,5 метра і W = 8,9 метра. Помножте довжину та ширину, щоб знайти площу.

\[\text{Area} \approx (22.5 \text{ m})(8.9 \text{ m}) ≈ 200.25 \text{ m}^2.\nonumber \]

Відзначимо, що це дуже майже точна площа 200 квадратних метрів. Невідповідність обумовлена тим, що ми знайшли довжину, округлену до найближчої десятої частки метра.

Вправа

Собачий біг Ета має форму прямокутника площею 500 квадратних футів. Якщо довжина бігу 28 футів, знайдіть ширину бігу, поправте до найближчої десятої частини ноги.

Відповідь: 17,9 футів

Приклад 10

Дитячі квитки в цирк надходять у продаж за $6,75. Клуб хлопчиків і дівчаток Eureka має $1,000 виділені на придбання цих квитків. Приблизно скільки квитків може придбати клуб Girls and Boys?

Рішення

Ми будемо слідувати Вимоги до вирішення проблем Word.

1. Налаштуйте словник змінних. Нехай N представляють кількість квитків, придбаних Клубом хлопчиків і дівчаток Еврики.

2. Налаштуйте рівняння. Зверніть увагу, що

\[ \begin{matrix} \colorbox{cyan}{Price per ticket} & \text{ times } & \colorbox{cyan}{Number of tickets} & \text{ is } & \colorbox{cyan}{Full Purchase Price} \\ 6.75 & . & N & = & 1,000 \end{matrix}\nonumber \]

Значить, наше рівняння дорівнює 6,75 N = 1000.

3. Розв'яжіть рівняння. Розділіть обидві сторони рівняння на 6,75.

\[ \begin{aligned} \frac{6.75N}{6.75} = \frac{1000}{6.75} ~ & \textcolor{red}{ \text{ Divide both sides by 6.75.}} \\ N \approx 148 ~ & \textcolor{red}{ \text{ Truncate to nearest unit.}} \end{aligned}\nonumber \]

Натисніть десяткову крапку до правого кінця дільника, а десяткову крапку в дивіденді рівну кількість знаків.

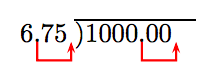
$Знімок екрана 2019-09-11 о 5.05.02 PM.png$

Ми зупинимо поділ на позиції одиниць.

$Знімок екрана 2019-09-11 о 5.05.05 PM.png$

4. Дайте відповідь на питання. Клуб Boys and Girls може придбати 148 квитків.

5. Озирніться назад. Давайте розрахуємо вартість 148 квитків по $6,75 за штуку.

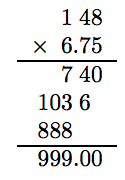
$Знімок екрана 2019-09-11 о 5.06.55 PM.png$

Таким чином, в $6,75 за штуку 148 квитків обійдуться в 999 доларів. Оскільки клуб хлопчиків і дівчаток Eureka має $1,000 для роботи, зверніть увагу, що в клубі не вистачає грошей на інший квиток.

Вправа

Дорослі квитки в цирк коштують $12,25 за штуку. Якщо клуб має $1,200 відведені для придбання квитків для дорослих, скільки квитків для дорослих вони можуть придбати?

Відповідь: 97

Приклад 11

Марта має 20 футів декоративної огорожі, яку вона буде використовувати для кордону невеликого круглого саду. Знайдіть діаметр круглого саду, поправте до найближчих сотих футів. Використовуйте π ≈ 3.14.

Рішення

Формула, що регулює співвідношення між окружністю і діаметром кола, дорівнює

\[C = \pi d\nonumber \]

20 футів декоративної огорожі будуть окружністю круглого саду. Замініть 20 на C і 3,14 на π.

\[20 = 3.14d\nonumber \]

Розділіть обидві сторони рівняння на 3,14.

\[ \begin{aligned} \frac{20}{3.14} = \frac{3.14d}{3.14} \\ \frac{20}{3.14} = d \end{aligned}\nonumber \]

Перемістіть десяткову крапку в кінець дільника, потім перемістіть десяткову крапку в дивіденді на рівну кількість знаків (два розряди) вправо. Зверніть увагу, що ми повинні додати два кінцевих нулі в дивіденді.

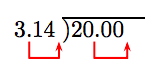
$Знімок екрана 2019-09-11 о 5.09.59 PM.png$

Таким чином, проблемою стає:

\[ 314 \overline{ )2000}\nonumber \]

Нам потрібно округлити до найближчої сотої. Для цього потрібно провести поділ на одне додаткове місце праворуч від сотих місць (тобто на тисячне місце).

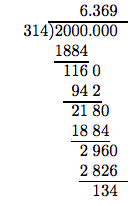
$Знімок екрана 2019-09-16 о 2.02.59 PM.png$

Для заключного кроку ми повинні округлити 6,369 до найближчої сотої. На схемі, що далі, ми створили цифру сотих («округлення цифра») і «тестова цифра», яка слідує за «округленням цифри».

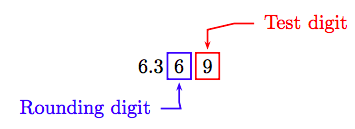
$Знімок екрана 2019-09-16 о 2.03.52 PM.png$

Оскільки «тестова цифра» більше або дорівнює 5, до «округлення цифрі» додаємо 1, потім обрізаємо. Тому до найближчої сотої стопи діаметр кола дорівнює приблизно

\[d ≈ 6.37 \text{ ft.}\nonumber \]

Вправа

Ділан має кругову собачу ручку з окружністю 100 футів. Знайдіть радіус пера, поправте до найближчої десятої частини фута. Використовуйте π ≈ 3.14.

Відповідь: 15,9 футів

Вправи

У вправах 1-16 розв'яжіть рівняння.

1. $5.57x − 2.45x = 5.46$

2. $−0.3x − 6.5x = 3.4$

3. $−5.8x + 0.32 + 0.2x = −6.96$

4. $−2.2x − 0.8 − 7.8x = −3.3$

5. $−4.9x + 88.2 = 24.5$

6. $−0.2x − 32.71 = 57.61$

7. $0.35x − 63.58 = 55.14$

8. $−0.2x − 67.3 = 93.5$

9. $−10.3x + 82.4=0$

10. $−1.33x − 45.22 = 0$

11. $−12.5x + 13.5=0$

12. $44.15x − 8.83 = 0$

13. $7.3x − 8.9 − 8.34x = 2.8$

14. $0.9x + 4.5 − 0.5x = 3.5$

15. $−0.2x + 2.2x = 6.8$

16. $−7.9x + 2.9x = 8.6$

У вправах 17-34 розв'яжіть рівняння.

17. $6.24x − 5.2=5.2x$

18. $−0.6x + 6.3=1.5x$

19. $−0.7x − 2.4 = −3.7x − 8.91$

20. $3.4x − 4.89 = 2.9x + 3.6$

21. $−4.9x = −5.4x + 8.4$

22. $2.5x = 4.5x + 5.8$

23. $−2.8x = −2.3x − 6.5$

24. $1.2x = 0.35x − 1.36$

25. $−2.97x − 2.6 = −3.47x + 7.47$

26. $−8.6x − 2.62 = −7.1x + 8.54$

27. $−1.7x = −0.2x − 0.6$

28. $3.89x = −5.11x + 5.4$

29. $−1.02x + 7.08 = −2.79x$

30. $1.5x − 2.4=0.3x$

31. $−4.75x − 6.77 = −7.45x + 3.49$

32. $−1.2x − 2.8 = −0.7x − 5.6$

33. $−4.06x − 7.38 = 4.94x$

34. $−4.22x + 7.8 = −6.3x$

У вправах 35-52 розв'яжіть рівняння.

35. $2.3+0.1(x + 2.9) = 6.9$

36. $−6.37 + 6.3(x + 4.9) = −1.33$

37. $0.5(1.5x − 6.58) = 6.88$

38. $0.5(−2.5x − 4.7) = 16.9$

39. $−6.3x − 0.4(x − 1.8) = −16.03$

40. $−2.8x + 5.08(x − 4.84) = 19.85$

41. $2.4(0.3x + 3.2) = −11.4$

42. $−0.7(0.2x + 5.48) = 16.45$

43. $−0.8(0.3x + 0.4) = −11.3$

44. $7.5(4.4x + 7.88) = 17.19$

45. $−7.57 − 2.42(x + 5.54) = 6.95$

46. $5.9 − 0.5(x + 5.8) = 12.15$

47. $−1.7 − 5.56(x + 6.1) = 12.2$

48. $−7.93 + 0.01(x + 7.9) = 14.2$

49. $4.3x − 0.7(x + 2.1) = 8.61$

50. $1.5x − 4.5(x + 4.92) = 15.6$

51. $−4.8x + 3.3(x − 0.4) = −7.05$

52. $−1.1x + 1.3(x + 1.3) = 19.88$

У вправах 53-58 розв'яжіть рівняння.

53. $0.9(6.2x − 5.9) = 3.4(3.7x + 4.3) − 1.8$

54. $0.4(−4.6x+ 4.7) = −1.6(−2.2x+ 6.9)−4.5$

55. $−1.8(−1.6x + 1.7) = −1.8(−3.6x − 4.1)$

56. $−3.3(−6.3x + 4.2) − 5.3=1.7(6.2x + 3.2)$

57. $0.9(0.4x + 2.5) − 2.5 = −1.9(0.8x + 3.1)$

58. $5.5(6.7x + 7.3) = −5.5(−4.2x + 2.2)$

59. Стейсі працює бізнес зі свого будинку, роблячи пташині будиночки. Щомісяця вона має постійні витрати в розмірі 200 доларів. Крім того, за кожен пташиний будиночок, який вона робить, вона несе додаткові витрати в розмірі 3.00 доларів. Якщо її загальні витрати за місяць становили $296.00, скільки пташиних будиночків вона зробила?

60. Стелла веде бізнес зі свого будинку, роблячи штори. Щомісяця вона має постійні витрати в розмірі 175 доларів. Крім того, за кожну штору, яку вона робить, вона несе додаткові витрати в розмірі 2,75 долара. Якщо її загальні витрати за місяць становили 274,00 доларів, скільки штор вона зробила?

61. У стаціонарному магазині у продажу є степлери за $1,50 за штуку. Бізнес купує невідоме їх кількість, а загальна вартість їх покупки становить $36,00. Скільки було придбано?

62. У стаціонарному магазині у продажу є компакт-пакети за $2.50 за штуку. Бізнес купує невідоме їх кількість, а загальна вартість їх покупки становить 40,00 доларів. Скільки було придбано?

63. Джулі веде бізнес зі свого будинку, роблячи скатертини. Щомісяця вона має постійні витрати в розмірі 100 доларів. Крім того, за кожну скатертину, яку вона виготовляє, вона несе додаткові витрати в розмірі 2,75 долара. Якщо її загальні витрати за місяць становили 221,00 доларів, скільки скатертин вона зробила?

64. Стелла веде бізнес зі свого будинку, роблячи ковдри. Щомісяця вона має постійні витрати в розмірі 200 доларів. Крім того, за кожну ковдру, яку вона робить, вона несе додаткові витрати в розмірі 1,75 долара. Якщо її загальні витрати за місяць становили $280,50, скільки ковдр вона зробила?

65. Марта має 60 футів декоративної огорожі, яку вона буде використовувати для кордону невеликого круглого саду. Знайдіть діаметр круглого саду, поправте до найближчих сотих футів. Використовуйте π ≈ 3.14.

66. Трійця має 44 фути декоративної огорожі, яку вона буде використовувати для кордону невеликого круглого саду. Знайдіть діаметр круглого саду, поправте до найближчих сотих футів. Використовуйте π ≈ 3.14.

67. Дитячі квитки на крижані капади надходять у продаж за $4,25. YMCA Сакраменто має $1,000 виділені на придбання цих квитків. Приблизно скільки квитків може придбати YMCA Сакраменто?

68. Дитячі квитки на крижані капади надходять у продаж за 5 доларів. Лицарі Колумба має $1,200 виділені для придбання цих квитків. Приблизно скільки квитків можуть придбати «Лицарі Колумба»?

69. У стаціонарному магазині в продажу є механічні олівці за $2,25 за штуку. Бізнес купує невідоме їх кількість, а загальна вартість їх покупки становить $65.25. Скільки було придбано?

70. Стаціонарний магазин має в продажу інженерні шаблони за $2.50 за штуку. Бізнес купує невідоме їх кількість, а загальна вартість їх покупки становить 60,00 доларів. Скільки було придбано?

71. Марта має 61 фут декоративної огорожі, яку вона буде використовувати для кордону невеликого круглого саду. Знайдіть діаметр круглого саду, поправте до найближчих сотих футів. Використовуйте π ≈ 3.14.

72. Кеті має 86 футів декоративної огорожі, яку вона буде використовувати для кордону невеликого круглого саду. Знайдіть діаметр круглого саду, поправте до найближчих сотих футів. Використовуйте π ≈ 3.14.

73. Кеті потрібно створити прямокутний садовий ділянку площею 100 квадратних метрів (100 м ²). Якщо ширина ділянки 7,5 метра, знайдіть довжину ділянки правильною до найближчої десятої частки метра.

74. Маріанні потрібно створити прямокутний садовий ділянку площею 223 квадратних метра (223 м ²). Якщо ширина ділянки 8,3 метра, знайдіть довжину ділянки правильною до найближчої десятої частки метра.

75. Дитячі квитки на стокові автомобільні гонки надходять у продаж за $4,5. Клуб хлопчиків і дівчаток Eureka має 1300 доларів, виділених для придбання цих квитків. Приблизно скільки квитків може придбати клуб хлопчиків і дівчаток Еврика?

76. Дитячі квитки в кіно надходять у продаж за $4,75. Клуб Lions Alameda має 800 доларів, відведених на придбання цих квитків. Приблизно скільки квитків може придбати Lions club of Alameda?

77. Ешлі потрібно створити прямокутний садовий ділянку площею 115 квадратних метрів (115 м ²). Якщо ширина ділянки 6,8 метра, знайдіть довжину ділянки правильною до найближчої десятої частки метра.

78. Моллі потрібно створити прямокутний садовий ділянку площею 268 квадратних метрів (268 м ²). Якщо ширина ділянки 6,1 метра, знайдіть довжину ділянки правильною до найближчої десятої частки метра.

79. Інвентаризація сирої сировини. Комерційні запаси сирої нафти в США скоротилися на 3,8 млн барелів за тиждень, що закінчився 19 червня. Якби на наступному тижні було 353,9 млн барелів, які були запаси сирої нафти до зниження? rttnews.com 06/24.09

80. Недокументовані. У 2008 році в Каліфорнії було 2,7 мільйона недокументованих жителів. Це подвоєне число в 1990 році. Скільки жителів без документів було в Каліфорнії в 1990 році? Асоційований прес Часи Стандарт 4/15/09

81. Діаманти сяючі. Індекс заломлення n вказує на кількість разів повільніше, що світлова хвиля рухається в певному середовищі, ніж вона рухається у вакуумі. Алмаз має показник заломлення 2,4. Це приблизно в один і в чверть разів перевищує показник заломлення циркону. Який показник заломлення циркону? Округляйте свій результат до найближчої десятої.

Відповіді

1. 1,75

3. 1.3

5. 13

7. 339,2

9. 8

11. 1.08

13. −11.25

15. 3.4

17. 5

19. −2.17

21. 16,8

23. 13

25. 20.14

27. 0,4

29. −4

31. 3.8

33. −0,82

35. 43,1

37. 13,56

39. 2,5

41. −26.5

43. 45,75

45. −11.54

47. −8.6

49. 2,8

51. 3.82

53. −2.59

55. −2.9

57. −3

59. 32

61. 24

63. 44

65. 19,11 фут (ів)

67. 235 квитків

69. 29

71. 19,43 фут (ів)

73. 13,3 метра

75. 288 квитків

77. 16,9 метрів

79. 357,7 млн барелів

81. 1.9