Skip to main content
LibreTexts - Ukrayinska

5.6: Дроби та десяткові

  1. Last updated
  2. Save as PDF
  • Page ID
    57294

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    При перетворенні дробу в десятковий може статися тільки одна з двох речей. Або процес завершиться, або десяткове подання почне повторювати візерунок цифр. У кожному випадку процедура зміни дробу на десятковий однаковий.

    Зміна дробу на десятковий

    Щоб змінити дріб на десятковий, розділіть чисельник на знаменник. Підказка: Якщо ви спочатку зменшите дріб до найнижчих, числа будуть меншими, і в результаті ділення буде трохи легше.

    Завершення десяткових знаків

    Закінчення десяткових знаків

    Спочатку зменшіть дріб до найнижчих показників. Якщо знаменник отриманого дробу має просту факторизацію, що складається строго з двійки і/або п'ятірки, то десяткове подання «закінчиться».

    Приклад 1

    Змініть 15/48 на десяткову.

    Рішення

    По-перше, зменшіть дріб до найнижчих показників.

    \[ \begin{aligned} \frac{15}{48} = \frac{3 \cdot 5}{3 \cdot 16} \\ = \frac{5}{16} \end{aligned}\nonumber \]

    Далі зверніть увагу, що знаменник 5/16 має просту факторизацію 16 = 2·2·2·2 · 2. Він складається тільки з двійки. Отже, десяткове подання 5/16 має закінчуватися.

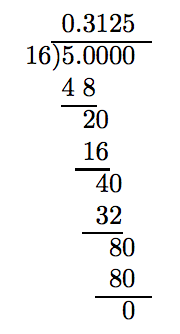
    Знімок екрана 2019-09-11 в 2.53.28 PM.png

    Нульовий залишок завершує процес. Значить, 5/16 = 0,3125.

    Вправа

    Змініть 10/16 на десяткову.

    Відповідь

    0,625

    Приклад 2

    \(3 \frac{7}{20}\)Змінити на десяткову.

    Рішення

    Зверніть увагу, що 7/20 зводиться до найнижчих членів і його знаменник має просту факторизацію 20 = 2 · 2 · 5. Він складається тільки з двійки і п'ятірки. Отже, десяткове подання 7/20 має закінчуватися.

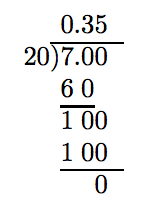
    Знімок екрана 2019-09-11 в 2.56.31 PM.png

    Нульовий залишок завершує процес. Значить, 7/20 = 0,35. Отже,\(3 \frac{7}{20}\) = 3,35.

    Вправа

    \(7 \frac{11}{20}\)Змінити на десяткову.

    Відповідь

    7.55

    Повторення десяткових знаків

    Повторення десяткових знаків

    Спочатку зменшіть дріб до найнижчих показників. Якщо просте факторизація отриманого знаменника не складається строго з двійки і п'ятірки, то процес ділення ніколи не матиме залишку нуля. Однак повторювані закономірності цифр повинні врешті-решт розкритися.

    Приклад 3

    Змініть 1/12 на десяткову.

    Рішення

    Зверніть увагу, що 1/12 зводиться до найнижчих членів і знаменник має просту факторизацію 12 = 2 · 2 · 3, яка не складається строго з двійки і п'ятірки. Отже, десяткове подання 1/12 не буде «припинено». Проводити поділ потрібно до тих пір, поки не з'явиться залишок вдруге. Це буде свідчити про початок повторення.

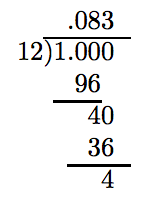
    Знімок екрана 2019-09-11 в 2.59.21 PM.png

    Зверніть увагу на другий вигляд 4 як залишок у поділі вище. Це вказівка на те, що повторення починається. Однак, щоб бути впевненим, давайте проведемо поділ ще на пару місць.

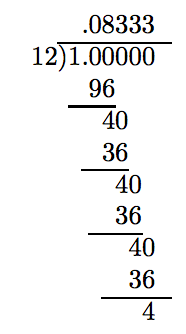
    Знімок екрана 2019-09-11 в 2.59.32 PM.png

    Зверніть увагу, як решта 4 повторюється знову і знову. У частці зверніть увагу, як цифра 3 повторюється знову і знову. Цілком очевидно, що якби ми проводили поділ ще на кілька місць, ми б отримали

    \[\frac{1}{12} = 0.833333 \cdots\nonumber \]

    Трикрапка - це символічний спосіб сказати, що трійки повторяться назавжди. Це математичний еквівалент слова «etcetera».

    Вправа

    Змініть 5/12 на десяткову.

    Відповідь

    0.41666...

    Існує альтернативне позначення крапки, а саме

    \[ \frac{1}{12} = 0.08 \overline{3}.\nonumber \]

    Смуга над 3 (називається «повторюваною смугою») вказує на те, що 3 буде повторюватися нескінченно довго. Тобто,

    \[0.08 \overline{3} = 0.083333 ....\nonumber \]

    Використання повторюваної смуги

    Щоб використовувати позначення повторюваної смуги, візьміть будь-який блок цифр під повторюваним рядком і дублюйте цей блок цифр нескінченно праворуч.

    Таким чином, наприклад:

    • \(5. \overline{345} = 5.3454545 ....\)
    • \(0. \overline{142857} = 0.142857142857142857 ....\)

    Важливе спостереження

    Хоча також\(0.8 \overline{33}\) буде виробляти 0.8333333..., як правило, ми повинні використовувати якомога менше цифр під повторюваною смугою. Таким чином,\(0.8 \overline{3}\) є кращим перед\(0.8 \overline{33}\).

    Приклад 4

    Змініть 23/111 на десяткову.

    Рішення

    Знаменник 23/111 має просту факторизацію 111 = 3 ·37 і не складається строго з двійки і п'ятірки. Отже, десяткове подання не буде «припинено». Нам потрібно виконувати поділ, поки не помітимо повторюваний залишок.

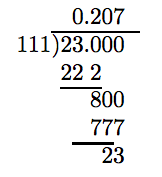
    Знімок екрана 2019-09-11 о 3.05.59 PM.png

    Зверніть увагу на повернення 23 як залишок. Таким чином, цифра в частці повинна починатися заново, але давайте додамо ще кілька місць до нашого поділу, щоб бути впевненим.

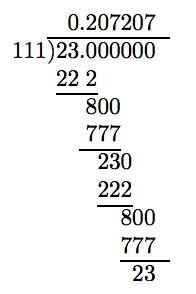
    Знімок екрана 2019-09-11 о 3.07.29 PM.png

    Ага! Знову залишок 23. Повторення! На даний момент ми впевнені, що

    \[ \frac{23}{111} = 0.207207 ....\nonumber \]

    Використовуючи «повторювану смугу», цей результат можна записати

    \[ \frac{23}{111} = 0. \overline{207}.\nonumber \]

    Вправа

    Змініть 5/33 на десяткову.

    Відповідь

    0.151515...

    Вирази, що містять як десяткові, так і дроби

    У цей момент ми можемо перетворити дроби в десяткові числа, і навпаки, ми можемо перетворити десяткові дроби в дроби. Тому ми повинні мати можливість оцінювати вирази, які містять суміш дробових і десяткових чисел.

    Приклад 5

    Спростити:\(- \frac{3}{8} - 1.25\).

    Рішення

    Давайте змінимо 1.25 на неправильний дріб.

    \[ \begin{aligned} 1.25 = \frac{125}{100} ~ & \textcolor{red}{ \text{ Two decimal places } \Rightarrow \text{ two zeroes.} \\ = \frac{5}{4} ~ & \textcolor{red}{ \text{ Reduce to lowest terms.}} \end{aligned}\nonumber \]

    У початковій задачі замініть 1,25 на 5/4, зробіть еквівалентні дроби загальним знаменником, потім відніміть.

    \[ \begin{aligned} - \frac{3}{8} - 1.25 = - \frac{3}{8} - \frac{5}{4} ~ & \textcolor{red}{ \text{ Replace 1.25 with 5/4.}} \\ = - \frac{3}{8} - \frac{5 \cdot \textcolor{red}{2}}{4 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 8.}} \\ = - \frac{3}{8} - \frac{10}{8} ~ & \textcolor{red}{ \text{ Simplify the numerator and denominator.}} \\ = - \frac{3}{8} + \left( - \frac{10}{8} \right) ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ = = \frac{13}{8} ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]

    Таким чином, −3/8 − 1,25 = −13/8.

    Альтернативне рішення

    Оскільки значення −3/8 зводиться до найнижчих, а 8 = 2 ·2 ·2 складається лише з двох, десяткове подання −3/8 завершиться.

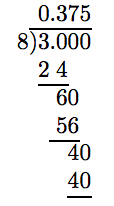
    Знімок екрана 2019-09-11 о 3.12.05 PM.png

    Отже, −3/8 = −0,375. Тепер замініть −3/8 у вихідній задачі на −0.375, а потім спростіть.

    \[ \begin{aligned} - \frac{3}{8} - 1.25 = -0.375 - 1.25 ~ & \textcolor{red}{ \text{ Replace } -3/8 \text{ with } -0.375.} \\ =-0.375 + (-1.25) ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ = -1.625 ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]

    Таким чином, −3/8 − 1,25 = −1,625.

    Вони однакові?

    Перший метод дав −13/8 як відповідь; другий метод дав −1,625. Це однакові результати? Один із способів з'ясувати це — змінити −1.625 на неправильний дріб.

    \[ \begin{aligned} -1.625 = - \frac{1625}{1000} ~ & \textcolor{red}{ \text{ Three places } \Rightarrow \text{ three zeroes.}} \\ = - \frac{5 \cdot 5 \cdot 5 \cdot 5 \cdot 13}{2 \cdot 2 \cdot 2 \cdot 5 \cdot 5 \cdot 5} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = - \frac{13}{2 \cdot 2 \cdot 2} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{13}{8} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

    Таким чином, дві відповіді однакові.

    Вправа

    Спростити:\(− \frac{7}{8} − 6.5\)

    Відповідь

    \(−7 \frac{3}{8}\)або −7,375

    Приклад 6

    Спростити:\(-\frac{2}{3} + 0.35\).

    Рішення

    Давайте атакуємо цей вираз, спочатку змінивши 0.35 на дріб.

    \[ \begin{aligned} - \frac{2}{3} + 0.35 = - \frac{2}{3} + \frac{35}{100} ~ & \textcolor{red}{ \text{ Change 0.35 to a fraction.}} \\ = - \frac{2}{3} + \frac{7}{20} ~ & \textcolor{red}{ \text{ Reduce 35/100 to lowest terms.}} \end{aligned}\nonumber \]

    Знайдіть РК-дисплей, зробіть еквівалентні дроби, потім додайте.

    \[ \begin{aligned} = - \frac{2 \cdot 20}{3 \cdot 20} + \frac{7 \cdot 3}{20 \cdot 3} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 60.}} \\ = - \frac{40}{60} + \frac{21}{60} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = - \frac{19}{60} ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]

    Потім,\(-\frac{2}{3} +0.35 = - \frac{19}{60}\).

    Вправа

    Спростити:\(-\frac{4}{9} + 0.25\)

    Відповідь

    −7/36

    У прикладі 6 ми зіткнемося з проблемами, якщо спробуємо змінити −2/3 на десяткову. Десяткове подання для −2/3 є повторюваним десятковим (знаменник не складається лише з двох і п'ятірок). Дійсно, −2/3 =\(−0. \overline{6}\). Щоб додати\(−0. \overline{6}\) і 0.35, ми повинні вирівняти десяткові крапки, а потім почати додавання в правому кінці. Але не\(−0. \overline{6}\) має правильного кінця! Це спостереження призводить до наступної поради.

    Важливе спостереження

    При представленні задачі, що містить як десяткові, так і дроби, якщо десяткове подання будь-якого дробу повторюється, то краще спочатку змінити всі числа на дроби, потім спростити.

    Вправи

    У вправах 1-20 перетворіть заданий дріб в кінцевий десятковий.

    1. \(\frac{59}{16}\)

    2. \(\frac{19}{5}\)

    3. \(\frac{35}{4}\)

    4. \(\frac{21}{4}\)

    5. \(\frac{1}{16}\)

    6. \(\frac{14}{5}\)

    7. \(\frac{6}{8}\)

    8. \(\frac{7}{175}\)

    9. \(\frac{3}{2}\)

    10. \(\frac{15}{16}\)

    11. \(\frac{119}{175}\)

    12. \(\frac{4}{8}\)

    13. \(\frac{9}{8}\)

    14. \(\frac{5}{2}\)

    15. \(\frac{78}{240}\)

    16. \(\frac{150}{96}\)

    17. \(\frac{25}{10}\)

    18. \(\frac{2}{4}\)

    19. \(\frac{9}{24}\)

    20. \(\frac{216}{150}\)

    У вправах 21-44 перетворіть заданий дріб у повторюваний десятковий. Використовуйте позначення «повторювана смуга».

    21. \(\frac{256}{180}\)

    22. \(\frac{268}{180}\)

    23. \(\frac{364}{12}\)

    24. \(\frac{292}{36}\)

    25. \(\frac{81}{110}\)

    26. \(\frac{82}{99}\)

    27. \(\frac{76}{15}\)

    28. \(\frac{23}{9}\)

    29. \(\frac{50}{99}\)

    30. \(\frac{53}{99}\)

    31. \(\frac{61}{15}\)

    32. \(\frac{37}{18}\)

    33. \(\frac{98}{66}\)

    34. \(\frac{305}{330}\)

    35. \(\frac{190}{495}\)

    36. \(\frac{102}{396}\)

    37. \(\frac{13}{15}\)

    38. \(\frac{65}{36}\)

    39. \(\frac{532}{21}\)

    40. \(\frac{44}{60}\)

    41. \(\frac{26}{198}\)

    42. \(\frac{686}{231}\)

    43. \(\frac{47}{66}\)

    44. \(\frac{41}{198}\)

    У вправах 45-52 спростіть заданий вираз, спочатку перетворивши дріб у кінцевий десятковий.

    45. \(\frac{7}{4} − 7.4\)

    46. \(\frac{3}{2} − 2.73\)

    47. \(\frac{7}{5} + 5.31\)

    48. \(− \frac{7}{4} + 3.3\)

    49. \(\frac{9}{10} − 8.61\)

    50. \(\frac{3}{4} + 3.7\)

    51. \(\frac{6}{5} − 7.65\)

    52. \(− \frac{3}{10} + 8.1\)

    У вправах 53-60 спростити заданий вираз, попередньо перетворивши десяткове число в дріб.

    53. \(\frac{7}{6} − 2.9\)

    54. \(− \frac{11}{6} + 1.12\)

    55. \(− \frac{4}{3} − 0.32\)

    56. \(\frac{11}{6} − 0.375\)

    57. \(− \frac{2}{3} + 0.9\)

    58. \(\frac{2}{3} − 0.1\)

    59. \(\frac{4}{3} − 2.6\)

    60. \(− \frac{5}{6} + 2.3\)

    У вправах 61-64 спростіть даний вираз.

    61. \(\frac{5}{6} + 2.375\)

    62. \(\frac{5}{3} + 0.55\)

    63. \(\frac{11}{8} + 8.2\)

    64. \(\frac{13}{8} + 8.4\)

    65. \(− \frac{7}{10} + 1.2\)

    66. \(− \frac{7}{5} − 3.34\)

    67. \(− \frac{11}{6} + 0.375\)

    68. \(\frac{5}{3} − 1.1\)

    Відповіді

    1. 3,6875

    3. 8,75

    5. 0.0625

    7. 0,75

    9. 1,5

    11. 0,68

    13. 1,125

    15. 0,325

    17. 2,5

    19. 0,375

    21. \(1.4 \overline{2}\)

    23. \(30. \overline{3}\)

    25. \(0.7 \overline{36}\)

    27. \(5.0 \overline{6}\)

    29. \(0. \overline{50}\)

    31. \(4.0 \overline{6}\)

    33. \(1. \overline{48}\)

    35. \(0. \overline{38}\)

    37. \(0.8 \overline{6}\)

    39. \(25. \overline{3}\)

    41. \(0. \overline{13}\)

    43. \(0.7 \overline{12}\)

    45. —5,65

    47. 6,71

    49. —7,71

    51. −6,45

    53. \(− \frac{26}{15}\)

    55. \(− \frac{124}{75}\)

    57. \(\frac{7}{30}\)

    59. \(− \frac{19}{15}\)

    61. \(\frac{77}{24}\)

    63. 9,575

    65. 0,5

    67. \(− \frac{35}{24}\)