5.4: Множення десяткових знаків

Множення десяткових чисел включає в себе два кроки: (1) множення чисел як цілих чисел, ігнорування десяткової крапки та (2) розміщення десяткової крапки в правильному положенні у добутку або відповіді.

Для прикладу розглянемо (0.7) (0.08), який просить нас знайти твір «сім десятих» і «вісім сотих». Ми могли б змінити ці десяткові числа на дроби, а потім помножити.

\[ \begin{aligned} (0.7)(0.8) & = \frac{7}{10} \cdot \frac{8}{100} \\ & = \frac{56}{100} \\ & = 0.056 \end{aligned}\nonumber \]

Твір - 56/1000, або «п'ятдесят шість тисячних», яке як десяткове число пишеться 0,056.

Важливі спостереження

Існує два дуже важливих спостереження щодо прикладу (0.7) (0.08).

1. У дробовій формі

\[\frac{7}{10} \cdot \frac{8}{100} = \frac{56}{1000},\nonumber \]

Зверніть увагу, що чисельник твору знаходять, взявши добуток цілих чисел 7 і 8. Тобто ви ігноруєте десяткові крапки в 0,7 і 0,08 і множите 7 і 8 так, ніби це цілі числа.

2. Перший множник, 0,7, має одну цифру праворуч від десяткової крапки. Його дробовий еквівалент, 7/10, має один нуль у своєму знаменнику. Другий множник, 0,08, має дві цифри праворуч від десяткової крапки. Його дробовий еквівалент, 8/100, має два нулі у своєму знаменнику. Отже, добуток 56/1000 змушений мати три нулі у своєму знаменнику, а його десятковий еквівалент, 0,056, повинен мати три цифри праворуч від десяткової крапки.

Давайте розглянемо інший приклад.

Приклад 1

Спрощення: (2.34) (1.2).

Рішення

Змініть десяткові числа «два і тридцять чотири соті» і «одна і дві десяті» на дроби, потім перемножте.

\[ \begin{aligned} (2.34)(1.2) = 2 \frac{34}{100} \cdot 1 \frac{2}{10} ~ & \textcolor{red}{ \text{ Change decimals to fractions.}} \\ = \frac{234}{100 \cdot \frac{12}{10} ~ & \textcolor{red}{ \text{ Change mixed to improper fractions.}} \\ = \frac{2808}{1000} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = 2 \frac{808}{1000} ~ & \textcolor{red}{ \text{ Change to mixed fraction.}} \\ = 2.808 ~ & \textcolor{red}{ \text{ Change back to decimal form.}} \end{aligned}\nonumber \]

Вправа

Помножити: (1,86) (9.5)

Відповідь

17.67

Важливі спостереження

Робимо ті ж два спостереження, що і в попередньому прикладі.

1. Якщо розглядати десяткові числа як цілі числа без десяткових крапок, то (234) (12) = 2808, який є чисельником дробу 2808/1000 у розв'язку, показаному в прикладі 1. Це також ті ж цифри, показані у відповіді 2.808.
2. Праворуч від десяткової крапки в першому множнику 2.34 є дві цифри і одна цифра праворуч від десяткової крапки у другому множнику 1.2. Це всього три цифри праворуч від десяткових знаків у множниках, що є точно такою ж кількістю цифр, які з'являються праворуч від десяткової крапки у відповіді 2.808.

Спостереження, зроблені в кінці попередніх двох прикладів, призводять нас до наступного методу.

Множення десяткових чисел

Щоб помножити два десяткових числа, виконайте наступні дії:

1. Ігноруйте десяткові крапки в множниках і помножте два множники так, ніби вони цілі числа.
2. Підрахуйте кількість цифр праворуч від десяткової крапки в кожному множнику. Підсумуйте ці два числа.
3. Поставте десяткову крапку у добутку так, щоб кількість цифр праворуч від десяткової крапки дорівнювала сумі, знайденій на кроці 2.

Приклад 2

Скористайтеся кроками, описаними в розділі Множення десяткових чисел, щоб знайти продукт у прикладі 1.

Рішення

Ми слідуємо крокам, описаним у розділі Множення десяткових чисел.

1. Насамперед необхідно помножити множники 2.34 і 1.2 як цілі числа, ігноруючи десяткові крапки.

\[ \begin{array}{r} 234 \\ \times 12 \\ \hline 468 \\ 234 \\ \hline 2808 \end{array}\nonumber \]

2. Другий крок - знайти суму кількості цифр праворуч від десяткових крапок в кожному множнику. Зверніть увагу, що 2.34 має дві цифри праворуч від десяткової крапки, тоді як 1.2 має одну цифру праворуч від десяткової крапки. Таким чином, ми маємо в цілому три цифри праворуч від десяткових крапок в множниках.

3. Третій і останній крок - поставити десяткову крапку в твір або відповідь так, щоб праворуч від десяткової крапки було три цифри. Таким чином,

(2,34) (1,2) = 2.808.

Зауважте, що це точно таке ж рішення, знайдене в прикладі 1.

Далі зручний спосіб оформити свою роботу у вертикальному форматі.

\[ \begin{array}{r} 2.34 \\ \times 1.2 \\ \hline 468 \\ 2 ~ 34 \\ \hline 2.808 \end{array}\nonumber \]

Вправа

Помножити: (5.98) (3.7)

Відповідь

22.126

Приклад 3

Спрощення: (8.235) (2.3).

Рішення

Ми використовуємо зручний вертикальний формат, введений в кінці Прикладу 2.

\[ \begin{array}{r} 8.235 \\ \times 2.3 \\ \hline 2~4705 \\ 16 ~ 470 \\ \hline 18.9405 \end{array}\nonumber \]

Коефіцієнт 8.235 має три цифри праворуч від десяткової крапки; множник 2.3 має одну цифру праворуч від десяткової крапки. Тому праворуч від десяткової крапки в добутку або відповіді має бути чотири цифри.

Вправа

Помножити: (9,582) (8.6)

Відповідь

82.4052

Множення знакових десяткових чисел

Правила, що регулюють множення знакових десяткових чисел, ідентичні правилам, що регулюють множення цілих чисел.

Як Знаки. Добуток двох десяткових чисел з подібними знаками є додатним. Тобто:

(+) (+) = + і (−) (−) = +

На відміну від знаків. Добуток двох десяткових чисел з несхожими знаками від'ємний. Тобто:

(+) (−) = − і (−) (+) = −

Приклад 4

Спростити: (−2.22) (−1.23).

Рішення

Ігноруйте знаки, щоб зробити множення, а потім розглянути ознаки в остаточній відповіді позаду.

Оскільки кожен множник має дві цифри праворуч від десяткової крапки, праворуч від десяткової крапки в добутку має бути 4 десяткових знака.

\[ \begin{array}{r} 2.22 \\ \times 1.23 \\ \hline \\ 666 \\ 444 \\ 1~11 \\ \hline 1.6206 \end{array}\nonumber \]

Подібні знаки дають позитивний продукт. Звідси:

(−2,22) (−1,23) = 1,6206

Вправа

Множення: (−3.86) (−5.77)

Відповідь

22.2722

Приклад 5

Спростити: (5.68) (−0.012).

Рішення

Ігноруйте знаки, щоб зробити множення, а потім розглянемо знаки в остаточній відповіді нижче.

Перший множник має дві цифри праворуч від десяткової крапки, другий множник - три. Тому праворуч від десяткової крапки в добутку або відповіді має бути всього п'ять цифр. Це обумовлює необхідність додавання зайвого нуля перед нашим продуктом.

\[ \begin{array}{r} 5.68 \\ \times 0.012 \\ \hline 1136 \\ 568 \\ \hline 0.06816 \end{array}\nonumber \]

На відміну від знаків дають негативний продукт. Звідси:

(5.68) (−0.012) = −0.06816

Вправа

Помножити: (9.23) (−0.018)

Відповідь

−0,1614

Порядок операцій

Ті самі Правила, що керують порядком операцій, також застосовуються до десяткових чисел.

Правила, що керують порядком операцій

При оцінці виразів дійте в наступному порядку.

1. Спочатку оцініть вирази, що містяться в символах групування. Якщо символи групування вкладені, спочатку оцініть вираз у внутрішній парі символів групування.
2. Оцінити всі показники, які з'являються у виразі.
3. Виконуйте всі множення і ділення в тому порядку, щоб вони відображалися у виразі, рухаючись зліва направо.
4. Виконуйте всі додавання і віднімання в тому порядку, щоб вони відображалися у виразі, рухаючись зліва направо.

Приклад 6

Якщо a = 3.1 і b = −2.4, оцініть a ² − ^{3,2 b 2}

Рішення

Підготуйте вираз для підстановки за допомогою дужок.

\[a^2 − 3.2b^2 = (~)^2 − 3.2(~)^2\nonumber \]

Замініть 3.1 на a та −2.4 для b та спростити.

\[ \begin{aligned} a^2 - 3.2b^2 = (3.1)^2 -3.2(-2.4)^2 ~ & \textcolor{red}{ \text{ Substitute: 3.1 for } a, ~ -2.4 \text{ for } b.} \\ =9.61 - 3.2(5.76) ~ & \textcolor{red}{ \text{ Exponents first: } (3.1)^2 = 9.61,~ (-2.4)^2 = 5.76} \\ =9.61 - 18.432 ~ & \textcolor{red}{ \text{ Multiply: } 3.2(5.76)=18.432} \\ = -8.822 ~ & \textcolor{red}{ \text{ Subtract: } 9.61 - 18.432 = -8.822} \end{aligned}\nonumber \]

Вправа

Якщо a = 3.8 і b = −4,6, оцініть вираз: 2.5 a ² − b ²

Відповідь

14.94

повноваження десяти

Розглянемо:

\[ \begin{array}{l}10^1 = 10 \\ 10^2 = 10 \cdot 10 = 100 \\ 10^3 = 10 \cdot 10 \cdot 10 = 1,000 \\ 10^4 = 10 \cdot 10 \cdot 10 \cdot 10 = 10,000 \end{array}\nonumber \]

Зверніть увагу на відповідь для 10 ⁴, один, за яким слідують чотири нулі! Ви бачите візерунок?

повноваження десяти

У ^{виразі 10 n} показник відповідає кількості нулів у відповіді. Отже, 10 ⁿ буде 1, а потім n нулів.

Приклад 7

Спрощення: 10 ⁹.

Рішення

10 ⁹ має бути 1, а потім 9 нулів. Тобто,

\[10^9 = 1, 000, 000, 000,\nonumber \]

або «один мільярд».

Вправа

Спрощення: 10 ⁶

Відповідь

1 000 000

Множення десяткових чисел на ступені десяти

Помножимо 1,234567 на 10 ³, або еквівалентно, на 1000. Ігноруйте десяткову крапку і помножте числа як цілі числа.

\[ \begin{array}{r} 1.234567 \\ \times 1000 \\ \hline 1234.567000 \end{array}\nonumber \]

Сума цифр праворуч від десяткової крапки в кожному множнику дорівнює 6. Тому ставимо десяткову крапку в добутку так, щоб праворуч від десяткової крапки було шість цифр.

Однак кінцеві нулі можуть бути видалені без зміни вартості товару. Тобто 1,234567 разів 1000 це 1234.567. Зверніть увагу, що десяткова крапка у добутку знаходиться на три розряди далі праворуч, ніж у вихідному коефіцієнті. Це спостереження призводить до наступного результату.

Множення десяткового числа на ступінь десяти

Множення десяткового числа на 10 ^{n призведе} до переміщення десяткової крапки на n знаків вправо.

Приклад 8

Спрощення: 1,234567 · 10 ⁴

Рішення

Множення на 104 (або еквівалентно, на 10 000) переміщує десяткові 4 розряди вправо. Таким чином, 1,234567 · 10 000 = 12345,67.

Вправа

Спрощення: 1,234567 · 10 ²

Відповідь

123.4567

Коло

Почнемо з визначення.

Коло

Коло - це сукупність всіх точок, рівновіддалених від заданої точки O, яка називається центром кола.

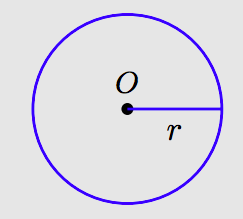
Відрізок, що з'єднує будь-яку точку на колі з центром кола, називається радіусом кола. На малюнку вище змінна r являє собою довжину радіуса кола

Нам потрібен ще один термін, діаметр кола.

Діаметр кола

Якщо дві точки на колі з'єднані з відрізком лінії, то цей відрізок називається хордою кола. Якщо хорда проходить через центр кола, то хорда називається діаметром кола.

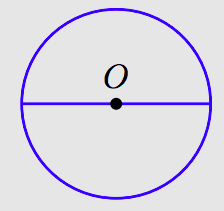
На малюнку вище змінна d представляє довжину діаметра кола. Зверніть увагу, що діаметр в два рази перевищує довжину радіуса; в символах

\[d=2r.\nonumber \]

Окружність кола

Коли ми працюємо з багатокутниками, периметр багатокутника знаходять шляхом підсумовування довжин його країв. Коло використовує іншу назву для свого периметра.

Окружність кола

Довжина кола називається його окружністю. Зазвичай ми використовуємо змінну C для позначення окружності кола.

Тобто, якщо ходити по колу, загальна відстань, пройдена за один оборот, - це окружність кола.

Стародавні математики Єгипту і Греції відзначали разючу залежність між окружністю кола і його діаметром. Вони виявили, що щоразу, коли ви ділите окружність кола на його діаметр, ви отримуєте постійну. Тобто, якщо взяти дуже велике коло і розділити його окружність на його діаметр, то вийде точно таке ж число, якщо взяти дуже маленьке коло і розділити його окружність на його діаметр. Ця загальна константа отримала назву π («пі»).

Пов'язання окружності та діаметра

Всякий раз, коли окружність кола ділиться на його діаметр, відповідь - постійна π. Тобто, якщо C - окружність кола, а d - діаметр кола, то

\[\frac{C}{d} = \pi.\nonumber \]

У сучасний час ми зазвичай множимо обидві сторони цього рівняння на d, щоб отримати формулу окружності кола.

\[C = \pi d\nonumber \]

Оскільки діаметр кола вдвічі перевищує довжину його радіуса, ми можемо замінити d = 2 r в останньому рівнянні, щоб отримати альтернативну форму рівняння окружності.

\[C = \pi (2r) = 2 \pi r\nonumber \]

Число π має багату і багатоповерхову історію. Стародавні геометри з Єгипту, Вавилонії, Індії та Греції знали, що π трохи більше 3. Найдавніші відомі наближення датуються приблизно 1900 р. До н.е. (Вікіпедія); вони 25/8 (Вавилонія) та 256/81 (Єгипет). Індійський текст Шатапатха Брахмана дає π як 339/108 ≈ 3.139. Архімед (287-212 рр. До н.е.) першим оцінив π, наближаючи окружність кола з вписаними та обмеженими багатокутниками. Він зміг довести, що 223/71 < π < 22/7. Беручи середнє значення цих значень, виходить π ≈ 3,1419. Сучасні математики довели, що π - це ірраціональне число, нескінченне десяткове число, яке ніколи не повторює жодної закономірності. Математики за допомогою комп'ютерів регулярно виробляють наближення π з мільярдами цифр після коми.

Цифри Pi

Ось π, поправте до перших п'ятдесяти цифр.

π = 3,14159265358979323846264338327950288419716939937510...

Кількість використовуваних цифр π залежить від застосування. Працюючи в дуже малих масштабах, можна тримати багато цифр π, але якщо ви будуєте круглий садовий паркан у вашому дворі, то менше цифр π потрібні.

Приклад 9

Знайдіть окружність кола, враховуючи його радіус 12 футів.

Рішення

Окружність кола задається формулою C = π d, або, тому що d = 2 r,

\[C = 2πr.\nonumber \]

Замініть 12 на r.

\[C = 2πr = 2π(12) = 24π\nonumber \]

Тому окружність кола дорівнює рівно C = 24π футів.

Ми можемо наблизити окружність, ввівши наближення для π. Скористаємося π ≈ 3.14. Примітка: Символ ≈ читається «приблизно дорівнює».

\[C = 24π ≈ 24(3.14) ≈ 75.36 \text{ feet}\nonumber \]

Важливо розуміти, що рішення C = 24π футів є точною окружністю, тоді як C ≈ 75.36 футів - це лише наближення.

Вправа

Знайдіть радіус кола, що має радіус 14 дюймів. Використовуйте π ≈ 3.14

Відповідь

87,92 дюймів

Площа кола

Ось розумний аргумент, який використовується, щоб допомогти розробити формулу для площі кола. Почніть з кола радіусом r і розділіть його на 8 рівних клинів, як показано на наступному малюнку.

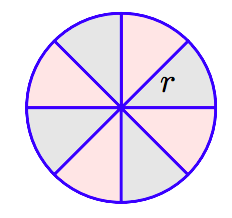
Переставте шматки, як показано на наступному малюнку.

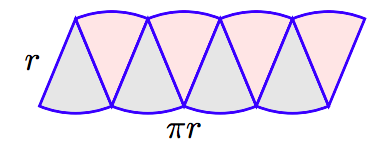
Зверніть увагу, що переставлені частини майже утворюють прямокутник довжиною приблизно на половину окружності кола, π r, а ширина приблизно r. Площа буде приблизно A ≈ (довжина) (ширина) ≈ (π r) (r) ≈ π r ². Це наближення було б ще краще, якби ми подвоїли кількість клинів кола.

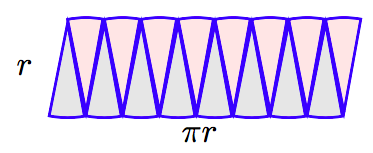
Якщо ми знову подвоїмо кількість клинів, вийшла фігура ще більше нагадувала б прямокутник з довжиною πr і шириною r Це призводить до наступного висновку.

Площа кола

Площа кола радіуса r задається за формулою

\[A = \pi r^2.\nonumber \]

приклад 10

Знайдіть площу кола, що має діаметр 12,5 метрів. Використовуйте 3,14 для π і округліть відповідь на площу до найближчої десятої частини квадратного метра.

Рішення

Діаметр в два рази більше радіуса.

\[d = 2r\nonumber \]

Заставте 12.5 на d і вирішіть для r.

\[ \begin{aligned} 12.5 = 2r ~ & \textcolor{red}{ \text{ Substitute 12.5 for } d.} \\ \frac{12.5}{2} = \frac{2r}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ 6.25 = r ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Значить, радіус становить 6,25 метра. Щоб знайти площу, скористайтеся формулою

\[A = \pi r^2\nonumber \]

і підставляємо: 3,14 для π і 6,25 для r.

\[ \begin{aligned} A = (3.14)(6.25)^2 ~ & \textcolor{red}{ \text{ Substitute: 3.14 for } \pi, \text{ 6.25 for } r.} \\ = (3.14)(39.0625) ~ & \textcolor{red}{ \text{ Square first: } (6.25)^2 = 39.0625} \\ =122.65625 ~ & \textcolor{red}{ \text{ Multiply: } (3.14)(39.0625) = 122.65625} \end{aligned}\nonumber \]

Значить, приблизна площа кола дорівнює А = 122,65625 квадратних метрів. Щоб округлити до найближчої десятої частини квадратного метра, визначте цифру округлення і контрольну цифру.

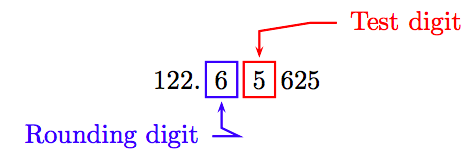
Оскільки тестова цифра більше або дорівнює 5, додайте 1 до цифри округлення і обрізайте. Таким чином, поправте до найближчої десятої частини квадратного метра площа кола приблизно

\[A ≈ 122.7 \text{ m}^2.\nonumber \]

Вправа

Знайдіть площу кола, що має радіус 12,2 сантиметра. Використовуйте π ≈ 3.14

Відповідь

467.3576 см ²

вправи

У вправах 1-28 помножте десяткові знаки.

1. (6.7) (0.03)

2. (2.4) (0.2)

3. (28.9) (5,9)

4. (33.5) (2.1)

5. (4.1) (4,6)

6. (2.6) (8.2)

7. (75.3) (0.4)

8. (21.4) (0.6)

9. (6,98) (0.9)

10. (2.11) (0.04)

11. (57.9) (3.29)

12. (3,58) (16.3)

13. (47.3) (0.9)

14. (30.7) (0.4)

15. (9,9) (6,7)

16. (7.2) (6.1)

17. (19.5) (7.9)

18. (43.4) (8,9)

19. (6,9) (0.3)

20. (7.7) (0.7)

21. (35.3) (3,81)

22. (5,44) (9,58)

23. (2,32) (0.03)

24. (4,48) (0.08)

25. (3.02) (6,7)

26. (1,26) (9,4)

27. (4,98) (6,2)

28. (3,53) (2.9)

---

У вправах 29-56 помножте десяткові знаки.

29. (−9.41) (0.07)

30. (4.45) (−0.4)

31. (−7.4) (−0.9)

32. (−6.9) (0.05)

33. (−8.2) (3.7)

34. (−7.5) (−6.6)

35. (9.72) (−9.1)

36. (6.22) (−9.4)

37. (−6.4) (2.6)

38. (2.3) (−4.4)

39. (−39.3) (−0.8)

40. (57.7) (−0.04)

41. (63.1) (−0.02)

42. (−51.1) (−0.8)

43. (−90.8) (3.1)

44. (−74.7) (2.9)

45. (47.5) (−82.1)

46. (−14.8) (−12.7)

47. (−31.1) (−4.8)

48. (−28.7) (−6.8)

49. (−2.5) (−0.07)

50. (−1.3) (−0.05)

51. (1.02) (−0.2)

52. (−7.48) (−0.1)

53. (7.81) (−5.5)

54. (−1,94) (4.2)

55. (−2.09) (37.9)

56. (20.6) (−15.2)

---

У вправах 57-68 помножте десяткове число на задану ступінь 10.

57. 24,264 · 10

58. 65,722 · 100

59. 53,867 · 10 ⁴

60. 23,216 · 10 ⁴

61. 5,096 · 10 ³

62. 60,890 · 10 ³

63. 37,968 · 10 ³

64. 43,552 · 10 ³

65. 61,303 · 100

66. 83,837 · 100

67. 74,896 · 1000

68. 30,728 · 100

---

У вправах 69-80 спростіть даний вираз.

69. (0.36) (7.4) − (−2.8) ²

70. (−8.88) (−9.2) − (−2.3) ²

71. 9.4 − (−7.7) (1.2) ²

72. 0.7 − (−8.7) (−9.4) ²

73. 5.94 − (−1.2) (−1.8) ²

74. −2.6 − (−9.8) (9.9) ²

75. 6,3 − 4,2 (9,3) ²

76. 9.9 − (−4.1) (8.5) ²

77. (6.3) (1.88) − (−2.2) ²

78. (−4.98) (−1.7) − 3,52

79. (−8.1) (9.4) − 1.8 ²

80. (−3.63) (5.2) − 0.8 ²

---

81. Задано a = −6.24, b = 0,4, а c = 7.2, оцініть вираз a − bc ².

82. Задано a = 4.1, b = −1.8, а c = −9.5, оцініть вираз a − bc ².

83. За даними a = −2.4, b = −2.1 та c = −4.6, обчислити вираз ab − c ².

84. Задано a = 3.3, b = 7.3, а c = 3.4, обчислити вираз ab − c ².

85. Задано a = −3.21, b = 3.5, а c = 8.3, обчислити вираз a − bc ².

86. Задано a = 7.45, b = −6.1, а c = −3.5, оцініть вираз a − bc ².

87. Задано a = −4.5, b = −6.9, а c = 4.6, обчислити вираз ab − c ².

88. За даними a = −8.3, b = 8.2 і c = 5.4, обчислити вираз ab − c ².

---

89. Коло має діаметр 8,56 дюймів. Використовуючи π ≈ 3,14, знайдіть окружність кола, поправте до найближчої десятої частини дюйма.

90. Коло має діаметр 14,23 дюйма. Використовуючи π ≈ 3,14, знайдіть окружність кола, поправте до найближчої десятої частини дюйма.

91. Коло має діаметр 12,04 дюйма. Використовуючи π ≈ 3,14, знайдіть окружність кола, поправте до найближчої десятої частини дюйма.

92. Коло має діаметр 14,11 дюйма. Використовуючи π ≈ 3,14, знайдіть окружність кола, поправте до найближчої десятої частини дюйма.

93. Коло має діаметр 10,75 дюйма. Використовуючи π ≈ 3,14, знайдіть площу кола, поправте до найближчої сотої квадратного дюйма.

94. Коло має діаметр 15,49 дюйма. Використовуючи π ≈ 3,14, знайдіть площу кола, поправте до найближчої сотої квадратного дюйма.

95. Коло має діаметр 13,96 дюйма. Використовуючи π ≈ 3,14, знайдіть площу кола, поправте до найближчої сотої квадратного дюйма.

96. Коло має діаметр 15,95 дюйма. Використовуючи π ≈ 3,14, знайдіть площу кола, поправте до найближчої сотої квадратного дюйма.

---

97. Сью вирішила побудувати круглий ставок для риб біля свого внутрішнього дворика. Вона хоче, щоб вона була 15 футів в діаметрі і 1,5 футів в глибину. Який обсяг води він буде утримувати? Використовуйте π ≈ 3.14. Підказка: Об'єм циліндра задається за формулою V = πr ² h, яка є площею круглої основи, помноженою на висоту циліндра.

98. Джон має рішення прийняти щодо його працевлаштування. В даний час він має роботу в Taco Loco в Фортуні. Після податків він заробляє близько $9.20 на годину і працює близько 168 годин на місяць. В даний час він платить 400 доларів на місяць за оренду. У нього є можливість переїхати до Санта-Рози і влаштуватися на роботу в Mi Ultimo Refugio, яка буде платити $10,30 на годину після податків протягом 168 годин на місяць, але його оренда коштувала б 570 доларів на місяць.

а) Після оплати житла в Фортуні, скільки у нього залишається щомісяця на інші витрати?

б) Після оплати житла в Санта-Розі, скільки б він залишив щомісяця на інші витрати?

в) На яку роботу у нього залишилося б більше грошей після сплати орендної плати і скільки б це було?

99. Джон вирішив переїхати до Санта-Рози і взяти роботу в Mi Ultimo Refugio (див. Вправа 98). Він зміг збільшити свій дохід, оскільки міг працювати 4 неділі на місяць у півтора години. Так що тепер він працював 32 години на місяць в півтора і 136 годин за звичайною ставкою $10,30 (все після того, як податки були зняті). Примітка: Раніше він працював 168 годин на місяць по 10,30 доларів на годину.

а) Яким був його новий щомісячний дохід?

б) На скільки збільшився його щомісячний дохід?

100. Електричний рахунок. За недавнім рахунком PGE стягував $0.11531 за кВт-год за перші 333 кВт-год використовуваної електроенергії. Якщо домогосподарство використовувало 312 кВт-год електроенергії, який був їхній рахунок за електроенергію?

101. Каберне. У долині Напа один акр хорошої землі може виробляти близько 3,5 тонн якісного винограду. При середній ціні $3,414 за тонну для преміум каберне, скільки грошей ви могли б генерувати на один акр каберне землеробства? Associated Press-Times-Standard 03/11/10 Виноградна міль загрожує методом вирощування доли

102. Добриво. Використовуючи митні ставки на ферму Огайо 2008 року, середня вартість поширення сухих об'ємних добрив становить близько $4.50 за акр. Яка вартість удобрювати 50 соток?

103. Агробізнес. Величезні корпоративні агробари вміщують по 1000 свиней.

а) Якщо кожна свиня важить приблизно 100 фунтів, скільки фунтів свині знаходиться на кожному складі?

б) При середньому 1,29 долара за фунт, яка загальна грошова вартість для корпоративного агросарану? Associated Press-Times-Стандарт 12/29/09 Підвищується тиск, щоб зупинити антибіотики в сільському

104. Корабельні аварії. Десяток багатовікових корабельних аварій виявила в Балтійському морі газова компанія, яка будує підводний трубопровід між Росією і Німеччиною. 12 затонулих аварій були знайдені в коридорі довжиною 30 миль і шириною 1,2 милі на глибині 430 футів. Змоделюйте коридор прямокутником і знайдіть приблизну площу регіону, де були знайдені кораблі. Associated Press-Times-Standard 03/10/10 Багатовікові корабельні аварії знайдені в Балтійському морі.

105. Радіо блюдо. Діаметр «флоту робочих коней» радіотелескопів, як і в Голдстоуні, штат Каліфорнія, становить 230 футів. Яка окружність тарілки радіотелескопа до найближчої десятої? Associated Press-Times-Стандарт 03/09/2010 NASA відремонтує антену глибокого космосу в пустелі Каліфорнії

---

Відповіді

1. 0,201

3. 170,51

5. 18,86

7. 30.12

9. 6,282

11. 190,491

13. 42.57

15. 66,33

17. 154.05

19. 2.07

21. 134,493

23. 0.0696

25. 20.234

27. 30.876

29. −0,6587

31. 6.66

33. —30.34

35. −88,452

37. −16.64

39. 31.44

41. −1,262

43. −281,48

45. -3899.75

47. 149.28

49. 0,175

51. −0,204

53. −42.955

55. -79.211

57. 242,64

59. 538670

61. 5096

63. 37968

65. 6130,3

67. 74896

69. −5.176

71. 20.488

73. 9,828

75. —356,958

77. 7,004

79. —79.38

81. —26.976

83. −16.12

85. −244,325

87. 9,89

89. 26,9 в.

91. 37,8 в.

93. 90,72 квадратних дюймів

95. 152,98 квадратних дюймів

97. 264.9375 кубічних футів

99.

а) $1895.20

б) $164,80

101. 11 949 доларів

103.

а) 100 000 фунтів

б) $129,000

105. 722,2 футів (ів)