4.6: Множення та ділення змішаних дробів

Почнемо з визначень належних і неправильних дробів.

Правильні та неправильні дроби

Правильний дріб - це дріб, чисельник якого менше його знаменника. Неправильний дріб - це дріб, чисельник якого більше його знаменника.

Наприклад,

\[ \frac{2}{3}, ~ - \frac{23}{39}, \text{ and } \frac{ 119}{127}\nonumber \]

всі приклади правильних дробів. З іншого боку,

\[ \frac{4}{3},~ - \frac{317}{123}, \text{ and } - \frac{233}{101}\nonumber \]

всі приклади неправильних дробів.

Змішаний дріб ¹ - це частина цілого числа, частина дробу.

Змішані фракції

Число

\[ 5 \frac{3}{4}\nonumber \]

називається змішаною фракцією. Визначається, що означає

\[5 \frac{3}{4} = 5 + \frac{3}{4}.\nonumber \]

У змішаному\(5 \frac{3}{4}\) дробі 5 - це ціла числова частина, а 3/4 - дробова.

Зміна змішаних дробів на неправильні дроби

У нас є всі інструменти, необхідні для перетворення змішаної фракції на неправильну фракцію. Почнемо з прикладу.

Приклад 1

Змішайте\(4 \frac{7}{8}\) змішану фракцію на неправильну.

Рішення

Використовуємо визначення змішаного дробу, робимо еквівалентний дріб для цілої числової частини, потім додаємо.

\[ \begin{aligned} 4 \frac{7}{8} = 4 + \frac{7}{8} ~ & \textcolor{red}{ \text{ By definition.}} \\ = \frac{4 \cdot \textcolor{red}{8}}{ \textcolor{red}{8}} + \frac{7}{8} ~ & \textcolor{red}{ \text{ Equivalent fraction with LCD = 8.}} \\ = \frac{4 \cdot 8 + 7}{8} ~ & \textcolor{red}{ \text{ Add numerators over common denominator.}} \\ = \frac{39}{8} ~ & \textcolor{red}{ \text{ Simplify the numerator.}} \end{aligned}\nonumber \]

Таким чином,\(4 \frac{7}{8}\) дорівнює 39/8.

Вправа

Зміна\(5 \frac{3}{4}\) на неправильний дріб.

Відповідь

23/4

Існує швидка методика, яку ви можете використовувати, щоб змінити змішану фракцію на неправильну.

Швидкий спосіб змінити змішаний дріб на неправильний дріб

Щоб змінити змішаний дріб на неправильний дріб, помножте всю числову частину на знаменник, додайте чисельник, потім помістіть результат над знаменником.

Таким чином, щоб швидко\(4 \frac{7}{8}\) перейти на неправильний дріб, помножте ціле число 4 на знаменник 8, додайте чисельник 7, потім помістіть результат над знаменником. У символах це виглядало б так:

\[ 4 \frac{7}{8} = \frac{4 \cdot 8 + 7}{8}.\nonumber \]

Саме так виглядає третій крок у прикладі 1; ми просто усуваємо багато роботи.

Приклад 2

Зміна\(4 \frac{2}{3}\) на неправильний дріб.

Рішення

Візьміть\(4 \frac{2}{3}\), помножте всю числову частину на знаменник, складіть чисельник, після чого поставте результат над знаменником.

\[4 \frac{2}{3} = \frac{4 \cdot 3 + 2}{3}\nonumber \]

Таким чином, результат

\[4 \frac{2}{3} = \frac{14}{3}.\nonumber \]

Вправа

Зміна\(7 \frac{3{8}\) на неправильний дріб.

Відповідь

59/8

Дуже легко зробити проміжний крок в прикладі 2 подумки, дозволяючи пропустити проміжний крок і перейти безпосередньо від змішаної дробу до неправильного дробу, не записуючи жодного біта роботи.

Приклад 3

Не записуючи жодної роботи, використовуйте ментальну арифметику,\(-2 \frac{3}{5}\) щоб перейти на неправильний дріб.

Рішення

\(−2 \frac{3}{5}\)Щоб перейти на неправильний дріб, ігноруйте знак мінус, дійте як і раніше, після чого приставте знак мінус до отриманого неправильного дробу. Отже, множимо 5 разів 2 і додаємо 3. Поставте результат 13 над знаменником 5, потім префіксуйте отриманий неправильний дріб зі знаком мінус. Тобто,

\[-2 \frac{3}{5} = - \frac{13}{5}.\nonumber \]

Вправа

Зміна\(-3 \frac{5}{12}\) на неправильний дріб.

Відповідь

−41/12

Зміна неправильних дробів на змішані

Першим кроком зміни неправильного дробу 27/5 на змішаний є запис неправильного дробу у вигляді суми.

\[\frac{27}{5} = \frac{25}{5} + \frac{2}{5}\nonumber \]

Спрощуючи рівняння 4.1, отримаємо

\[ \begin{aligned} \frac{27}{5} = 5 + \frac{2}{5} \\ = 5 \frac{2}{5} \end{aligned}\nonumber \]

Коментар. Ви не можете просто вибрати будь-яку суму. Сума, яка використовується в рівнянні 4.1, будується так, що перший дріб дорівнюватиме цілому числу, а другий - правильним. Будь-яка інша сума не зможе отримати правильний змішаний дріб. Наприклад, сума

\[ \frac{27}{5} = \frac{23}{5} + \frac{4}{5}\nonumber \]

марно, тому що 23/5 - це не ціле число. Аналогічно, сума

\[ \frac{27}{5} = \frac{20}{5} + \frac{7}{5}\nonumber \]

це не добре. Незважаючи на те, що 20/5 = 4 є цілим числом, другий дріб 7/5 все ще неправильний.

Приклад 4

Змінити 25/9 на змішаний дріб.

Рішення

Розбийте 25/9 на відповідну суму.

\[ \begin{aligned} \frac{25}{9} = \frac{18}{9} + \frac{7}{9} \\ = 2 + \frac{7}{9} \\ = 2 \frac{7}{9} \end{aligned}\nonumber \]

Вправа

Змінити 25/7 на змішаний дріб.

Відповідь

\(3 \frac{4}{7}\).

Коментар. Виникає закономірність. • У випадку 27/5 зверніть увагу, що 27 поділений на 5 дорівнює 5 з залишком 2. Порівняйте це з результатом змішаного дробу: 27/5 = 5 2 5 • У випадку з прикладом 4 зверніть увагу, що 25 ділиться на 9, дорівнює 2 з залишком 7. Порівняйте це з результатом змішаного дробу: 25/9=2 7 9. Ці спостереження мотивують наступну методику.

Швидкий спосіб змінити неправильний дріб на змішаний

Щоб змінити неправильний дріб на змішаний дріб, розділіть чисельник на знаменник. Частка буде цілою числовою частиною змішаного дробу. Якщо розмістити залишок над знаменником, це буде дробова частина змішаного дробу.

Приклад 5

Змінити 37/8 на змішаний дріб.

Рішення

37 ділиться на 8 дорівнює 4, з залишком 5. Тобто:

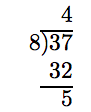
Частка стає цілою числовою частиною, і ми ставимо залишок над дільником. Таким чином,

\[ \frac{37}{8} = 4 \frac{5}{8}.\nonumber \]

Примітка: Ви можете перевірити свій результат за допомогою «Швидкого способу змінити змішаний дріб на неправильний дріб». 8 разів 4 плюс 5 дорівнює 37. Покладіть це на 8, щоб отримати 37/8.

Вправа

Змінити 38/9 на змішаний дріб.

Відповідь

\(4 \frac{2}{9}\)

Приклад 6

Змінити −43/5 на змішаний дріб.

Рішення

Ігноруйте знак мінус і дійте так само, як у прикладі 5. 43 ділиться на 5 дорівнює 8, з залишком 3.

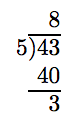
Частка - це ціла числова частина, потім ми ставимо залишок над дільником. Нарешті, приставка знака мінус.

\[ -\frac{43}{5} = -8 \frac{3}{5}\nonumber \]

Множення та ділення змішаних дробів

У вас є всі інструменти, необхідні для множення та поділу змішаних дробів. Спочатку змініть змішані дроби на неправильні, потім помножте або діліть, як це робили в попередніх розділах.

¹ Змішаний дріб іноді називають мішаним числом.

Приклад 7

Спростити:\(-2 \frac{1}{12} \cdot 2 \frac{4}{5}\).

Рішення

Змінити на неправильні дроби, коефіцієнт, скасувати і спростити.

\[ \begin{aligned} -2 \frac{1}{12} \cdot 2 \frac{4}{5} = - \frac{25}{12} \cdot \frac{14}{5} ~ & \textcolor{red}{ \text{ Change to improper fractions.}} \\ = - \frac{25 \cdot 14}{12 \cdot 5} ~ & \textcolor{red}{ \begin{aligned} \text{ Multiply numerators; multiply denominators.} \\ \text{ Unlike signs; product is negative.} \end{aligned}} \\ = - \frac{(5 \cdot 5) \cdot (2 \cdot 7)}{2 \cdot 2 \cdot 3) \cdot (5)} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = - \frac{ \cancel{5} \cdot 5 \cdot \cancel{2} \cdot 7}{ \cancel{2} \cdot 2 \cdot 3 \cdot \cancel{5}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{35}{6} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \end{aligned}\nonumber \]

Це цілком хороша відповідь, але якщо ви хочете відповідь змішаної дробу, 35 ділиться на 6 дорівнює 5, з залишком 5. Отже,

\[ -2 \frac{1}{12} \cdot 2 \frac{4}{5} = -5 \frac{5}{6}.\nonumber \]

Вправа\(\PageIndex{1}\)

Спростити:

\[-3 \frac{3}{4} \cdot 2 \frac{2}{5}\nonumber \]

Відповідь

−9

Приклад 8

Спростити:

\[-4 \frac{4}{5} \div 5 \frac{3}{5}.\nonumber \]

Рішення

Зміна на неправильні дроби, інвертувати і множити, коефіцієнт, скасувати, і спростити.

\[ \begin{aligned} -4 \frac{4}{5} \div 5 \frac{3}{5} = - \frac{24}{5} \div \frac{28}{5} ~ & \textcolor{red}{ \text{ Change to improper fractions.}} \\ = - \frac{24}{5} \cdot \frac{5}{28} ~ & \textcolor{red}{ \text{ Invert and multiply.}} \\ = - \frac{2 \cdot 2 \cdot 2 \cdot 3}{5} \cdot \frac{5}{2 \cdot 2 \cdot 7} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = - \frac{ \cancel{2} \cdot \cancel{2} \cdot 2 \cdot 3}{ \cancel{3}} \cdot \frac{ \cancel{5}}{ \cancel{2} \cdot \cancel{2} \cdot 7} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{6}{7} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \cdot \end{aligned}\nonumber \]

Вправа

Спростити:

\[-2 \frac{4}{9} \cdot 3 \frac{2}{3}\nonumber \]

Відповідь

−2/3

Вправи

У вправах 1-12 перетворіть змішаний дріб в неправильний дріб.

1. \(2 \frac{1}{3}\)

2. \(1 \frac{8}{11}\)

3. \(1 \frac{1}{19}\)

4. \(−1 \frac{1}{5}\)

5. \(−1 \frac{3}{7}\)

6. \(1 \frac{3}{17}\)

7. \(1 \frac{1}{9}\)

8. \(1 \frac{5}{11}\)

9. \(−1 \frac{1}{2}\)

10. \(−1 \frac{5}{8}\)

11. \(1 \frac{1}{3}\)

12. \(−1 \frac{5}{7}\)

---

У вправах 13-24 перетворіть неправильний дріб в змішаний дріб.

13. \(\frac{13}{7}\)

14. \(\frac{−17}{9}\)

15. \(\frac{−13}{5}\)

16. \(\frac{−10}{3}\)

17. \(\frac{−16}{5}\)

18. \(\frac{16}{13}\)

19. \(\frac{9}{8}\)

20. \(\frac{16}{5}\)

21. \(\frac{−6}{5}\)

22. \(\frac{−17}{10}\)

23. \(\frac{−3}{2}\)

24. \(\frac{−7}{4}\)

---

У вправах 25-48 помножте числа і висловіть свою відповідь як змішаний дріб.

25. \(1 \frac{1}{7} \cdot 2 \frac{1}{2}\)

26. \(1 \frac{1}{8} \cdot 1 \frac{1}{6}\)

27. \(4 \cdot 1 \frac{1}{6}\)

28. \(1 \frac{7}{10} \cdot 4\)

29. \( \left( −1 \frac{1}{12} \right) \left( 3 \frac{3}{4} \right)\)

30. \( \left( −3 \frac{1}{2} \right) \left( 3 \frac{1}{3} \right)\)

31. \(7 \frac{1}{2} \cdot 1 \frac{1}{13}\)

32. \(2 \frac{1}{4} \cdot 1 \frac{5}{11}\)

33. \( \left( 1 \frac{2}{13} \right) \left( −4 \frac{2}{3} \right)\)

34. \( \left( 1 \frac{1}{14} \right) \left( −2 \frac{2}{5} \right)\)

35. \( \left( 1 \frac{3}{7} \right) \left( −3 \frac{3}{4} \right)\)

36. \( \left( 1 \frac{4}{5} \right) \left( −3 \frac{3}{4} \right)\)

37. \(9 \cdot \left( −1 \frac{2}{15} \right)\)

38. \(4 \cdot \left( −2 \frac{5}{6} \right)\)

39. \( \left( −2 \frac{1}{8} \right) (−6)\)

40. \((−9) \left( −3 \frac{1}{6} \right)\)

41. \( \left( −4 \frac{1}{2} \right) \left( −2 \frac{2}{5} \right)\)

42. \( \left( −1 \frac{3}{7} \right) \left( −3 \frac{3}{4} \right)\)

43. \( \left( −2 \frac{1}{6} \right) \cdot 4\)

44. \((−6) \cdot \left( 1 \frac{1}{9} \right)\)

45. \( \left( −1 \frac{4}{15} \right) \left( 2 \frac{1}{2} \right)\)

46. \( \left( −1 \frac{1}{5} \right) \left( 1 \frac{5}{9} \right)\)

47. \( \left( −2 \frac{1}{2} \right) \left( −1 \frac{7}{11} \right)\)

48. \( \left( −1 \frac{7}{11} \right) \left( −1 \frac{7}{12} \right)\)

---

У вправах 49-72 розділіть змішані дроби і висловіть свою відповідь як змішаний дріб.

49. \(8 \div 2 \frac{2}{9}\)

50. \(4 \frac{2}{3} \div 4\)

51. \( \left( −3 \frac{1}{2} \right) \div \left( 1 \frac{1}{16} \right)\)

52. \( \left( −1 \frac{2}{5} \right) \div \left( 1 \frac{1}{15} \right)\)

53. \(6 \frac{1}{2} \div 1 \frac{7}{12}\)

54. \(5 \frac{1}{2} \div 1 \frac{9}{10}\)

55. \((−4) \div \left( 1 \frac{5}{9} \right)\)

56. \( \left( −4 \frac{2}{3} \right) \div 4\)

57. \( \left( −5 \frac{2}{3} \right) \div \left( −2 \frac{1}{6} \right)\)

58. \( \left( −2 \frac{1}{2} \right) \div \left( −2 \frac{2}{9} \right)\)

59. \( \left( −6 \frac{1}{2} \right) \div \left( 4 \frac{1}{4} \right)\)

60. \( \left( −1 \frac{1}{6} \right) \div \left( 1 \frac{1}{8} \right)\)

61. \((−6) \div \left( −1 \frac{3}{11} \right)\)

62. \( \left( −6 \frac{2}{3} \right) \div (−6)\)

63. \( \left( 4 \frac{2}{3} \right) \div (−4)\)

64. \( \left( 6 \frac{2}{3} \right) \div (−6)\)

65. \( \left( 1 \frac{3}{4} \right) \div \left( −1 \frac{1}{12} \right)\)

66. \( \left( 2 \frac{4}{7} \right) \div \left( −1 \frac{1}{5} \right)\)

67. \( \left( 5 \frac{2}{3} \right) \div 1 \frac{1}{9}\)

68. \( 1 \frac{2}{3} \div 1 \frac{2}{9}\)

69. \( \left( −7 \frac{1}{2} \right) \div \left( −2 \frac{2}{5} \right)\)

70. \( \left( −5 \frac{1}{3} \right) \div \left( −2 \frac{5}{6} \right)\)

71. \( \left( 3 \frac{2}{3} \right) \div \left( −1 \frac{1}{9} \right)\)

72. \( \left( 8 \frac{1}{2} \right) \div \left( −1 \frac{3}{4} \right)\)

---

73. Дрібні партії. Скільки партій чверті акрів можна зробити з\(6 \frac{1}{2}\) гектарів землі?

74. Велике поле. З\(17 \frac{1}{2}\) половини акрів утворилося поле. Скільки гектарів було отримане поле?

75. Ювелірні вироби. Щоб зробити деякі прикраси, брусок срібла довжиною\(4 \frac{1}{2}\) дюймів був розрізаний на шматочки довжиною\( \frac{1}{12}\) дюймів. Скільки штук було зроблено?

76. кекси. За цим рецептом вийде 6 мафінів: 1 склянка молока,\(1 \frac{2}{3}\) склянки борошна, 2 яйця, 1/2 чайної ложки солі,\(1 \frac{1}{2}\) чайні ложки розпушувача. Напишіть рецепт шести десятків мафінів.

---

Відповіді

1. \( \frac{7}{3}\)

3. \( \frac{20}{19}\)

5. \(− \frac{10}{7}\)

7. \( \frac{10}{9}\)

9. \(− \frac{3}{2}\)

11. \( \frac{4}{3}\)

13. \(1 \frac{6}{7}\)

15. \(−2 \frac{3}{5}\)

17. \(−3 \frac{1}{5}\)

19. \(1 \frac{1}{8}\)

21. \(−1 \frac{1}{5}\)

23. \(−1 \frac{1}{2}\)

25. \(2 \frac{6}{7}\)

27. \(4 \frac{2}{3}\)

29. \(−4 \frac{1}{16}\)

31. \(8 \frac{1}{13}\)

33. \(−5 \frac{5}{13}\)

35. \(−5 \frac{5}{14}\)

37. \(−10 \frac{1}{5}\)

39. \(12 \frac{3}{4}\)

41. \(10 \frac{4}{5}\)

43. \(− 8 \frac{2}{3}\)

45. \(− 3 \frac{1}{6}\)

47. \(4 \frac{1}{11}\)

49. \(3 \frac{3}{5}\)

51. \(− 3 \frac{5}{17}\)

53. \(4 \frac{2}{19}\)

55. \(− 2 \frac{4}{7}\)

57. \(2 \frac{8}{13}\)

59. \(− 1 \frac{9}{17}\)

61. \(4 \frac{5}{7}\)

63. \(− 1 \frac{1}{6}\)

65. \(− 1 \frac{8}{13}\)

67. \(5 \frac{1}{10}\)

69. \(3 \frac{1}{8}\)

71. \(− 3 \frac{3}{10}\)

73. 26 лотів площею чверть акра

75. 54 штуки