4.3: Множення дробів

Last updated
Save as PDF

Page ID: 57351

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Розглянемо зображення на малюнку 4.5, де вертикальні лінії ділять прямокутну область на три рівні частини. Якщо затінювати один з трьох рівних частин, затінена область становить 1/3 всієї прямокутної області.

Знімок екрана 2019-08-30 в 9.47.42 AM.png — Малюнок 4.5: Затінена область становить 1/3 всієї області.

Ми хотіли б візуалізувати беручи 1/2 з 1/3. Для цього ми намалюємо додаткову горизонтальну лінію, яка розділяє затінену область навпіл по горизонталі. Це показано на малюнку 4.6. Затінена область, яка представляла 1/3, тепер розділена на дві менші прямокутні області, одна з яких затінена іншим кольором. Цей регіон являє собою 1/2 з 1/3.

Знімок екрана 2019-08-30 в 9.47.49 AM.png — Малюнок 4.6: Затінення 1/2 з 1/3.

Далі продовжити горизонтальну лінію на всю ширину прямокутної області, як показано на малюнку 4.7.

Знімок екрана 2019-08-30 в 9.47.55 AM.png — Малюнок 4.7: Затінення 1/2 з 1/3.

Зверніть увагу, що малювання горизонтальної лінії в поєднанні з трьома оригінальними вертикальними лініями вдалося розділити повну прямокутну область на шість менших, але рівних частин, лише один з яких (той, що представляє 1/2 1/3) затінений новим кольором. Отже, цей щойно затінений шматок представляє 1/6 всієї області. Висновок нашого візуального аргументу полягає в тому, що 1/2 1/3 дорівнює 1/6. В символах,

\[ \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6} .\nonumber \]

Приклад 1

Створіть візуальний аргумент, який показує, що 1/3 2/5 дорівнює 2/15.

Рішення

Спочатку розділіть прямокутну область на п'ять рівних частин і розтушуйте дві з них. Це являє собою дріб 2/5.

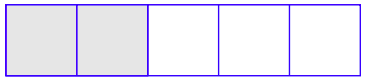
$Знімок екрана 2019-08-30 в 9.50.36 AM.png$

Далі намалюйте дві горизонтальні лінії, які ділять затінену область на три рівні частини і затіньте 1 з трьох рівних частин. Це являє собою прийняття 1/3 з 2/5.

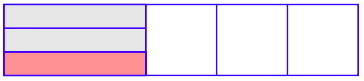
$Знімок екрана 2019-08-30 в 9.50.43 AM.png$

Далі продовжите горизонтальні лінії на всю ширину області і поверніть вихідну вертикальну лінію з першого зображення.

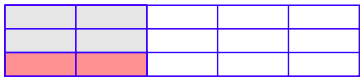
$Знімок екрана 2019-08-30 в 9.50.51 AM.png$

Зверніть увагу, що три горизонтальні лінії в поєднанні з п'ятьма оригінальними вертикальними лініями вдалося розділити всю область на 15 менших, але рівних частин, лише дві з яких (ті, що представляють 1/3 2/5) затінені новим кольором. Отже, цей нещодавно затінений шматок представляє 2/15 всієї області. Висновок цього візуального аргументу полягає в тому, що 1/3 з 2/5 дорівнює 2/15. В символах,

\[ \frac{1}{3} \cdot \frac{2}{5} = \frac{2}{15}.\nonumber \]

Вправа

Створіть візуальний аргумент, який показує, що 1/2 1/4 дорівнює 1/8.

Відповідь

Діаграма:

$Знімок екрана 2019-08-30 в 9.53.06 AM.png$

Правило множення

На малюнку 4.7 ми побачили, що 1/2 1/3 дорівнює 1/6. Зверніть увагу, що відбувається, коли ми множимо чисельники і множимо знаменники дробів 1/2 і 1/3.

\[ \begin{aligned} \frac{1}{2} \cdot \frac{1}{3} = \frac{1 \cdot 1}{2 \cdot 3} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{1}{6} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \end{aligned}\nonumber \]

Отримуємо 1/6!

Чи може це бути збіг чи удача? Давайте спробуємо, що ще раз з дробів з Приклад 1, де ми побачили, що 1/3 2/5 дорівнює 2/15. Знову множимо чисельники і знаменники на 1/3 і 2/5.

\[ \begin{aligned} \frac{1}{3} \cdot \frac{2}{5} = \frac{1 \cdot 2}{3 \cdot 5} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{2}{15} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \end{aligned}\nonumber \]

Знову отримуємо 2/15!

Ці два приклади мотивують наступне визначення.

Визначення: Правило множення

Щоб знайти добуток дробів a/b і c/d, перемножте їх чисельники і знаменники. В символах,

\[ \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d}\nonumber \]

Приклад 2

Помножте 1/5 і 7/9.

Рішення

Множимо чисельники і множимо знаменники.

\[ \begin{aligned} \frac{1}{5} \cdot \frac{7}{9} = \frac{1 \cdot 7}{5 \cdot 9} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{7}{45} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \end{aligned}\nonumber \]

Вправа

Помножити:

\[ \frac{1}{3} \cdot \frac{2}{5}\nonumber \]

Відповідь: Помножити:$ \frac{6}{15}$

Приклад 3

Знайдіть добуток −2/3 та 7/9.

Рішення

Звичайні правила знаків поширюються на продукцію. На відміну від знаків дає негативний результат.

\[ \begin{aligned} - \frac{2}{3} \cdot \frac{7}{9} = - \frac{2 \cdot 7}{3 \cdot 9} & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = - \frac{14}{27} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \end{aligned}\nonumber \]

Не потрібно, щоб ви фізично показували середню сходинку. Якщо ви хочете зробити це подумки, то ви можете просто написати

\[ - \frac{2}{3} \cdot \frac{7}{9} = - \frac{14}{27}.\nonumber \]

Вправа

Помножити:

\[ - \frac{3}{5} \cdot \frac{2}{7}\nonumber \]

Відповідь: \[ - \frac{6}{35}\nonumber \]

Помножити і зменшити

Після множення двох дробів переконайтеся, що ваша відповідь зменшена до найнижчих (див. Розділ 4.1).

Приклад 4

Помножте 3/4 рази 8/9.

Рішення

Після множення ділимо чисельник і знаменник на найбільший спільний дільник чисельника і знаменника.

\[ \begin{aligned} \frac{3}{4} \cdot \frac{8}{9} = \frac{3 \cdot 8}{4 \cdot 9} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = \frac{24}{36} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = \frac{24 \div 12}{36 \div 12} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by GCD.}} \\ = \frac{2}{3} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]

Крім того, після множення ви можете простий множник як чисельник, так і знаменник, а потім скасувати загальні множники.

\[ \begin{aligned} \frac{3}{4} \cdot \frac{8}{9} = \frac{24}{36} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = \frac{2 \cdot 2 \cdot 2 \cdot 3}{2 \cdot 2 \cdot 3 \cdot 3} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = = \frac{\cancel{2} \cdot \cancel{2} \cdot 2 \cdot \cancel{3}}{\cancel{2} \cdot \cancel{2} \cdot 3 \cdot \cancel{3}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{2}{3} ~ \end{aligned}\nonumber \]

Вправа

Помножити:

\[ \frac{3}{7} \cdot \frac{14}{9}\nonumber \]

Відповідь: \[ \frac{2}{3}\nonumber \]

Приклад 5

Помножте −7x/2 та 5/ (14x ²).

Рішення

Після множення, простий множник як чисельник, так і знаменник, потім скасовують загальні множники. Відзначимо, що на відміну від ознак дає негативний продукт.

\[ \begin{aligned} - \frac{7x}{2} \cdot \frac{5}{14x^2} = - \frac{35x}{28x^2} ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = - \frac{5 \cdot 7 \cdot x}{2 \cdot 2 \cdot 7 \cdot x \cdot x} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = - \frac{5 \cdot \cancel{7} \cdot \cancel{x}}{2 \cdot 2 \cdot \cancel{7} \cdot \cancel{x} \cdot x} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{5}{4x} \end{aligned}\nonumber \]

Вправа

Помножити:

\[ - \frac{3x}{2} \cdot \frac{6}{21x^3}\nonumber \]

Відповідь: \[ - \frac{3}{7x^2}\nonumber \]

Множення та скасування або скасування та множення

Коли ви працюєте з більшими числами, стає трохи складніше множити, коефіцієнт і скасувати. Розглянемо наступний аргумент.

\[ \begin{aligned} \frac{18}{30} \cdot \frac{35}{6} = \frac{630}{180} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{2 \cdot 3 \cdot 3 \cdot 5 \cdot 7}{2 \cdot 2 \cdot 3 \cdot 3 \cdot 5} ~ & \textcolor{red}{ \text{ Prime factor numerators and denominators.}} \\ = \frac{ \cancel{2} \cdot \cancel{3} \cdot \cancel{3} \cdot \cancel{5} \cdot 7}{2 \cdot \cancel{2} \cdot \cancel{3} \cdot \cancel{3} \cdot \cancel{5}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{7}{2} ~ & \textcolor{red}{ \text{ Remaining factors.}} \end{aligned}\nonumber \]

При такому підході є ряд складнощів. По-перше, вам доведеться множити великі числа, а по-друге, ви повинні простими множниками ще більші результати.

Один з можливих обхідних шляхів - не морочитися множенням чисельників і знаменників, залишаючи їх у факторованому вигляді.

\[ \begin{aligned} \frac{18}{30} \cdot \frac{35}{6} = \frac{18 \cdot 35}{30 \cdot 6} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \end{aligned}\nonumber \]

Знайти просту факторизацію цих менших факторів простіше.

\[ \begin{aligned} = \frac{(2 \cdot 3 \cdot 3) \cdot (5 \cdot 7)}{(2 \cdot 3 \cdot 5) \cdot (2 \cdot 3)} ~ & \textcolor{red}{ \text{ Prime factor.}} \end{aligned}\nonumber \]

Тепер ми можемо скасувати загальні фактори. Дужки більше не потрібні в чисельнику та знаменнику, оскільки обидва містять добуток простих множників, тому порядок та групування не мають значення.

\[ \begin{aligned} = \frac{ \cancel{2} \cdot \cancel{3} \cdot \cancel{3} \cdot \cancel{5} \cdot \cancel{7}}{ \cancel{2} \cdot \cancel{3} \cdot \cancel{5} \cdot 2 \cdot \cancel{3}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{7}{2} ~ & \textcolor{red}{ \text{ Remaining factors.}} \end{aligned}\nonumber \]

Інший підхід полягає в факторних чисельниках і знаменниках на місці, скасування загальних факторів, а потім множення.

\[ \begin{aligned} \frac{18}{30} \cdot \frac{35}{6} = \frac{2 \cdot 3 \cdot 3}{2 \cdot 3 \cdot 5} \cdot \frac{5 \cdot 7}{2 \cdot 3} ~ & \textcolor{red}{ \text{ Factor numerators and denominators.}} \\ = \frac{ \cancel{2} \cdot \cancel{3} \cdot \cancel{3} \cdot \cancel{3}}{ \cancel{2} \cdot \cancel{3} \cdot \cancel{5}} \cdot \frac{ \cancel{5} \cdot 7}{2 \cdot \cancel{3}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{7}{2} ~ & \textcolor{red}{ \text{ Remaining factors.}} \end{aligned}\nonumber \]

Зверніть увагу, що це дає точно такий же результат, 7/2.

Правило скасування

При множенні дробів скасуйте загальні множники за таким правилом: «Скасувати множник в чисельнику для ідентичного множника в знаменнику».

приклад 6

Знайдіть товар 14/15 і 30/140.

Рішення

Множимо чисельники і множимо знаменники. Просте множник, скасуйте загальні множники, потім множте.

\[ \begin{aligned} \frac{14}{15} \cdot \frac{30}{140} = \frac{14 \cdot 30}{15 \cdot 140} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = \frac{(2 \cdot 7) \cdot (2 \cdot 3 \cdot 5)}{(3 \cdot 5) \cdot (2 \cdot 2 \cdot 5 \cdot 7)} ~ & \textcolor{red}{ \text{ Prime factor numerators and denominators.}} \\ = \frac{ \cancel{2} \cdot \cancel{7} \cdot \cancel{2} \cdot \cancel{3} \cdot \cancel{5}}{ \cancel{3} \cdot 5 cdot \cancel{2} \cdot \cancel{2} \cdot \cancel{5} \cdot \cancel{7}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{1}{5} ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]

Примітка: Все в чисельнику скасовується, тому що ви розділили чисельник сам по собі. Значить, відповідь має 1 в своєму чисельнику.

Вправа

Помножити:

\[ \frac{6}{35} \cdot \frac{70}{36}\nonumber \]

Відповідь: $\frac{1}{3}$

Коли все скасовується

Коли всі множники в чисельнику скасовуються, це означає, що чисельник ви ділите самі по собі. Отже, ви залишаєтеся з 1 в чисельнику. Це ж правило поширюється і на знаменник. Якщо все в знаменнику скасовується, ви залишитеся з 1 в знаменнику.

приклад 7

Спрощення продукту:\ (-\ frac {6x} {55y}\ cdot\ ліворуч (-\ frac {110y^2} {105x^2}\ праворуч). \ номер\]

Рішення

Твір двох негативів - позитивний.

\[ \begin{aligned} - \frac{6x}{55y} \cdot \left( - \frac{110y^2}{105x^2} \right) = \frac{6x}{55y} \cdot \frac{110y^2}{105x^2} ~ & \textcolor{red}{ \text{ Like signs gives a positive.}} \end{aligned}\nonumber \]

Прості множники чисельники і знаменники, потім скасовують загальні множники.

\[ \begin{aligned} = \frac{2 \cdot 3 \cdot x}{5 \cdot 11 \cdot y} \cdot \frac{2 \cdot 5 \cdot 11 \cdot y \cdot y}{3 \cdot 5 \cdot 7 \cdot x \cdot x} ~ & \textcolor{red}{ \text{ Prime factor numerators & denominators.}} \\ = \frac{2 \cdot \cancel{3} \cdot \cancel{x}}{5 \cdot \cancel{11} \cdot \cancel{y}} \cdot \frac{2 \cdot \cancel{5} \cdot \cancel{11} \cdot \cancel{y} \cdot y}{ \cancel{3} \cdot \cancel{5} \cdot 7 \cdot \cancel{x} \cdot x} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{2 \cdot 2 \cdot y}{5 \cdot 7 \cdot x} ~ & \textcolor{red}{ \text{ Remaining factors.}} \\ = \frac{4y}{35x} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \end{aligned}\nonumber \]

Вправа

Спростити:

\[ \frac{6x}{15b} \cdot \left( - \frac{35b^2}{10a^2} \right)\nonumber \]

Відповідь: \[ - \frac{21b}{5a}\nonumber \]

Паралелограми

У цьому розділі ми дізнаємося, як знайти площу паралелограма. Почнемо з визначення паралелограма. Нагадаємо, що чотирикутник - це багатокутник, що має чотири сторони. Паралелограм - це дуже особливий тип чотирикутника.

Паралелограм

Паралелограм - це чотирикутник, протилежні сторони якого паралельні.

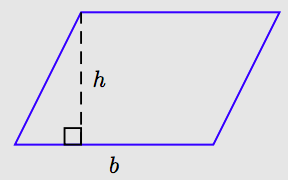
$Знімок екрана 2019-08-30 в 11.10.40 AM.png$

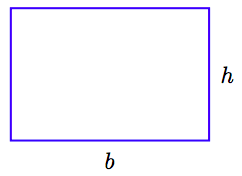
Сторона, на яку спирається паралелограм, називається його основою (позначено b на малюнку), а відстань від його заснування до протилежної сторони називається її висотою (позначено h на малюнку). Зверніть увагу, що висота перпендикулярна до основи (відповідає основі під кутом 90◦).

На малюнку 4.8 зображений прямокутник, що має довжину b і ширину h. Тому площа прямокутника на малюнку 4.8 дорівнює A = bh, яку знаходять, взявши добуток довжини і ширини. Візьміть ножиці і виріжте трикутник з правого кінця прямокутника, як показано на малюнку 4.9 (а), потім вставте вирізаний трикутник до лівого кінця, як показано на малюнку 4.9 (b). Результатом, показаним на малюнку 4.9 (b), є паралелограм, що має підставу b і висоту h.

Оскільки ми не викинули жодного матеріалу при створенні паралелограма з прямокутника, паралелограм має ту ж площу, що і вихідний прямокутник. Тобто площа паралелограма дорівнює A = bh.

Знімок екрана 2019-08-30 о 11.12.48 AM.png — Малюнок 4.8: Площа прямокутника дорівнює A = bh.

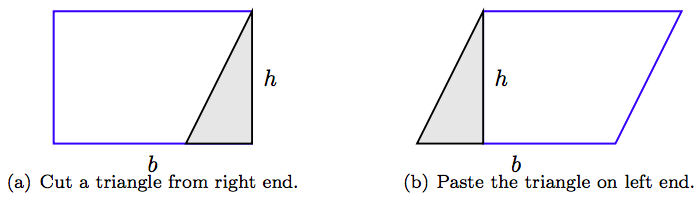
Знімок екрана 2019-08-30 в 11.13.27 AM.png — Малюнок 4.9: Створення паралелограма з прямокутника.

Площа паралелограма

Паралелограм, що має підставу b і висоту h, має площу A = bh. Тобто, щоб знайти площу паралелограма, беруть добуток його підстави і висоти.

приклад 8

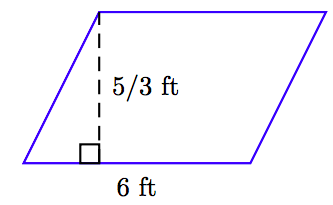
Знайдіть площу паралелограма, зображеної нижче.

$Знімок екрана 2019-08-30 в 11.15.04 AM.png$

Рішення

Площа паралелограма дорівнює добутку його підстави і висоти. Тобто,

\[ \begin{aligned} A = bh ~ & \textcolor{red}{ \text{ Area formula for a parallelogram.}} \\ = (6 \text{ ft}) \left( \frac{5}{3} \text{ ft} \right) ~ & \textcolor{red}{ \text{ Substitute: 6 ft for }b, \text{ 5/3 ft for } h.} \\ = \frac{30}{3} \text{ ft}^2. ~ & \textcolor{red}{ \text{ Multiply numerators and denominators.}} \\ = 10 \text{ ft}^2. ~ & \textcolor{red}{ \text{ Divide.}} \end{aligned}\nonumber \]

Таким чином, площа паралелограма становить 10 квадратних футів.

Вправа

Основа паралелограма вимірює 14 дюймів. Висота становить 8/7 дюйма. Яка площа паралелограма?

Відповідь: 16 квадратних дюймів

Трикутники

Звернемо увагу на те, як дізнатися, як знайти площу трикутника.

Трикутник

Трикутник - це тристоронній багатокутник. Вона утворюється шляхом побудови трьох точок і з'єднання їх трьома відрізками лінії. Кожна з трьох точок називається вершиною трикутника і кожен з трьох відрізків лінії називається стороною трикутника.

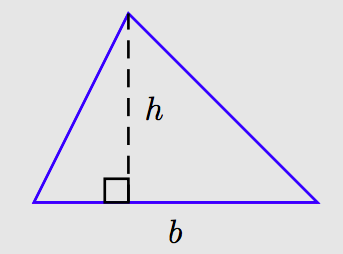
$Знімок екрана 2019-08-30 в 11.19.46 AM.png$

Сторона, на якій спирається трикутник, називається його підставою, а відстань між його підставою і протилежною вершиною називається його висотою висоти. Висота завжди перпендикулярна підставі; тобто вона утворює кут 90◦ з основою.

Легко помітити, що трикутник має половину площі паралелограма.

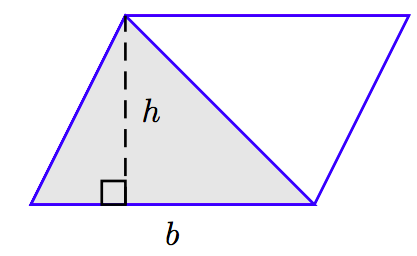
$Знімок екрана 2019-08-30 в 11.19.51 AM.png$

Паралелограм має площу A = bh. Тому трикутник має половину цієї площі. Тобто площа трикутника дорівнює A = (1/2) bh.

Площа трикутника

Трикутник, що має основу b і висоту h, має площу A = (1/2) bh. Тобто, щоб знайти площу трикутника, візьміть по половині добутку підстави і висоти.

приклад 9

Знайдіть площу трикутника, зображеної нижче.

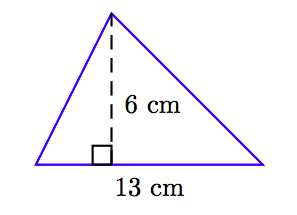
$Знімок екрана 2019-08-30 в 11.23.40 AM.png$

Рішення

Щоб знайти площу трикутника, візьміть по половині добутку підстави і висоти.

\[ \begin{aligned} A = \frac{1}{2} bh ~ & \textcolor{red}{ \text{ Area of a triangle formula.}} \\ = \frac{1}{2} (13 \text{ cm}) (6 \text{ cm}) ~ & \textcolor{red}{ \text{ Substitute: 13 cm for } b,~ \text{6 cm for } h.} \\ = \frac{78 \text{ cm}^2}{2} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = 39 \text{ cm}^2. ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Тому площа трикутника становить 39 квадратних сантиметрів.

Вправа

Підстава трикутника має розміри 15 метрів. Висота 12 метрів. Яка площа трикутника?

Відповідь: 90 квадратних метрів

Визначення бази та висоти

Іноді буває трохи складно визначити підставу і висоту (висоту) трикутника. Для прикладу розглянемо трикутник на малюнку 4.10 (а). Припустимо, ми вибираємо нижній край трикутника в якості основи і позначаємо його довжину змінною b, як показано на малюнку 4.10 (а).

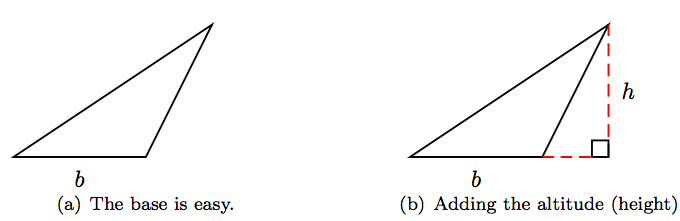
Знімок екрана 2019-08-30 о 11.28.19 AM.png — Малюнок 4.10: Визначення підстави і висоти (висоти) трикутника.

Висота (висота) трикутника визначається як відстань між основою трикутника і його протилежною вершиною. Щоб визначити цю висоту, ми повинні спочатку продовжити базу, як видно на пунктирному розширенні на малюнку 4.10 (b), потім скинути перпендикулярну пунктирну лінію від протилежної вершини до розширеної основи, також показаної на малюнку 4.10 (b). Цей перпендикуляр - висота (висота) трикутника і позначимо його довжину h.

Але ми можемо піти далі. Будь-яка з трьох сторін трикутника може бути позначена як основа трикутника. Припустимо, як показано на малюнку 4.11 (а), ми виділимо в якості основи іншу сторону, при цьому довжина позначається змінною b.

Висота до цього нового підстави буде відрізок від протилежної вершини, перпендикулярно до основи. Її довжина на малюнку 4.11 (б) позначається ч.

Подібним чином, є третя сторона трикутника, яка також може бути використана як основа. Висоту до цієї третьої сторони знаходять шляхом скидання перпендикуляра з вершини трикутника прямо протилежної від цієї основи. Це також зажадає розширення підстави. Ми залишаємо це для вивчення наших читачів.

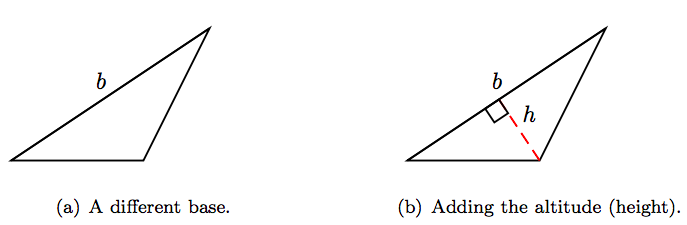
Знімок екрана 2019-08-30 о 11.30.30 AM.png — Малюнок 4.11: Визначення підстави і висоти (висоти) трикутника.

Ключовий момент

В якості основи може бути використана будь-яка з трьох сторін трикутника. Висота малюється скиданням перпендикуляра від протилежної вершини до обраної основи. Для цього іноді потрібно, щоб ми подовжували підставу. Незалежно від того, яку сторону ми використовуємо для основи, формула A = bh /2 дасть той же результат площі.

Вправи

1. Створіть діаграму, таку як показано на малюнку 4.7, щоб показати, що 1/3 1/3 дорівнює 1/9.

2. Створіть діаграму, таку як показано на малюнку 4.7, щоб показати, що 1/2 1/4 дорівнює 1/8.

3. Створіть діаграму, таку як показано на малюнку 4.7, щоб показати, що 1/3 1/4 дорівнює 1/12.

4. Створіть діаграму, таку як показано на малюнку 4.7, щоб показати, що 2/3 1/3 дорівнює 2/9.

У вправах 1-28 помножте дроби і спростіть свій результат.

5. $\frac{−21}{4} \cdot \frac{22}{19}$

6. $\frac{−4}{19} \cdot \frac{21}{8}$

7. $\frac{20}{11} \cdot \frac{−17}{22}$

8. $\frac{−9}{2} \cdot \frac{6}{7}$

9. $\frac{21}{8} \cdot \frac{−14}{15}$

10. $\frac{−17}{18} \cdot \frac{−3}{4}$

11. $\frac{−5}{11} \cdot \frac{7}{20}$

12. $\frac{−5}{2} \cdot \frac{−20}{19}$

13. $\frac{8}{13} \cdot \frac{−1}{6}$

14. $\frac{−12}{7} \cdot \frac{5}{9}$

15. $\frac{2}{15} \cdot \frac{−9}{8}$

16. $\frac{2}{11} \cdot \frac{−21}{8}$

17. $\frac{17}{12} \cdot \frac{3}{4}$

18. $\frac{7}{13} \cdot \frac{10}{21}$

19. $\frac{−6}{23} \cdot \frac{9}{10}$

20. $\frac{12}{11} \cdot \frac{−5}{2}$

21. $\frac{−23}{24} \cdot \frac{−6}{17}$

22. $\frac{4}{9} \cdot \frac{−21}{19}$

23. $\frac{24}{7} \cdot \frac{5}{2}$

24. $\frac{−20}{23} \cdot \frac{−1}{2}$

25. $\frac{1}{2} \cdot \frac{−8}{11}$

26. $\frac{−11}{18} \cdot \frac{−20}{3}$

27. $\frac{−24}{13} \cdot \frac{−7}{18}$

28. $\frac{21}{20} \cdot \frac{−4}{5}$

У вправах 29-40 помножте дроби, і спростіть свій результат.

29. $\frac{−12y^3}{13} \cdot \frac{2}{9y^6}$

30. $\frac{−8x^3}{3} \cdot \frac{−6}{5x^5}$

31. $\frac{11y^3}{24} \cdot \frac{6}{5y^5}$

32. $\frac{11y}{18} \cdot \frac{21}{17y^6}$

33. $\frac{−8x^2}{21} \cdot \frac{−18}{19x}$

34. $\frac{2y^4}{11} \cdot \frac{−7}{18y}$

35. $\frac{13x^6}{15} \cdot \frac{9}{16x^2}$

36. $\frac{−22x^6}{15} \cdot \frac{17}{16x^3}$

37. $\frac{−6y^3}{5} \cdot \frac{−20}{7y^6}$

38. $\frac{−21y}{5} \cdot \frac{−8}{3y^2}$

39. $\frac{−3y^3}{4} \cdot \frac{23}{12y}$

40. $\frac{−16y^6}{15} \cdot \frac{−21}{13y^4}$

У вправах 41-56 помножте дроби і спростіть свій результат.

41. $\frac{13y^6}{20x^4} \cdot \frac{2x}{7y^2}$

42. $\frac{−8y^3}{13x^6} \cdot \frac{7x^2}{10y^2}$

43. $\frac{23y^4}{21x} \cdot \frac{−7x^6}{4y^2}$

44. $\frac{−2x^6}{9y^4} \cdot \frac{y^5}{20x}$

45. $\frac{11y^6}{12x^6} \cdot \frac{−2x^4}{7y^2}$

46. $\frac{16x^3}{13y^4} \cdot \frac{11y^2}{18x}$

47. $\frac{x^6}{21y^3} \cdot \frac{−7y^4}{9x^5}$

48. $\frac{−3y^3}{5x} \cdot \frac{14x^5}{15y^2}$

49. $\frac{19y^2}{18x} \cdot \frac{10x^3}{7y^3}$

50. $\frac{−20x}{9y^3} \cdot \frac{−y^6}{4x^3}$

51. $\frac{−4y^3}{5x^5} \cdot \frac{−10x}{21y^4}$

52. $\frac{11y^2}{14x^4} \cdot \frac{−22x}{21y^3}$

53. $\frac{−16x}{21y^2} \cdot \frac{−7y^3}{5x^2}$

54. $\frac{−4y}{5x} \cdot \frac{10x^3}{7y^6}$

55. $\frac{17x^3}{3y^6} \cdot \frac{−12y^2}{7x^4}$

56. $\frac{−6x^4}{11y^3} \cdot \frac{13y^2}{8x^5}$

У вправах 57-62 знайдіть площу паралелограма, що має задану базу і висоту.

57. основа = 8 см, висота = 7 см

58. основа = 2 см, висота = 11 см

59. основа = 6 см, висота = 13 см

60. основа = 2 см, висота = 6 см

61. підстава = 18 см, висота = 14 см

62. підстава = 20 см, висота = 2 см

У вправах 63-68 знайдіть площу трикутника, показану на малюнку. (Примітка: Цифри не намальовані в масштабі.)

63.

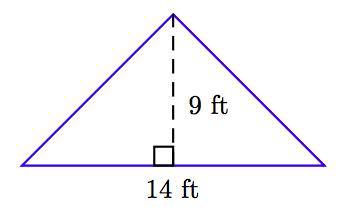
$Знімок екрана 2019-08-30 в 2.00.34 PM.png$

64.

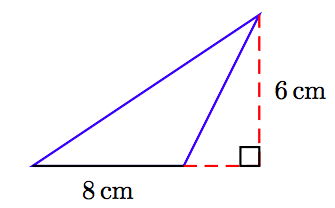
$Знімок екрана 2019-08-30 в 2.00.42 PM.png$

65.

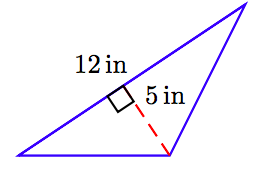
$Знімок екрана 2019-08-30 в 2.00.49 PM.png$

66.

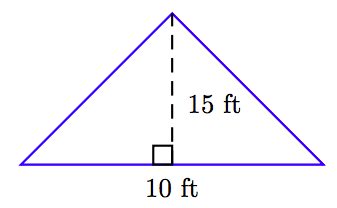
$Знімок екрана 2019-08-30 в 2.00.57 PM.png$

67.

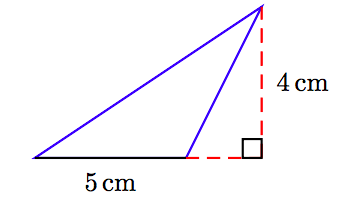
$Знімок екрана 2019-08-30 на 2.01.03 PM.png$

68.

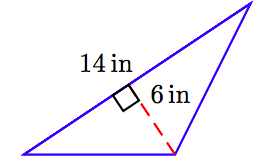
$Знімок екрана 2019-08-30 на 2.01.08 PM.png$

69. Вага на Місяці. На Місяці ви б зважували лише 1/6 від того, що ви важите на землі. Якщо ви важите 138 фунтів на землі, якою була б ваша вага на Місяці?

Відповіді

1. Це показує, що 1/3 1/3 дорівнює 1/9.

$Знімок екрана 2019-08-30 в 1.51.28 PM.png$

3. Це показує, що 1/3 1/4 дорівнює 1/12.

$Знімок екрана 2019-08-30 в 1.51.35 PM.png$

5. $\frac{−231}{38}$

7. $\frac{−170}{121}$

9. $\frac{−49}{20}$

11. $\frac{−7}{44}$

13. $\frac{−4}{39}$

15. $\frac{−3}{20}$

17. $\frac{17}{16}$

19. $\frac{−27}{115}$

21. $\frac{23}{68}$

23. $\frac{60}{7}$

25. $\frac{−4}{11}$

27. $\frac{28}{39}$

29. $− \frac{8}{39y^3}$

31. $\frac{11}{20y^2}$

33. $\frac{48x}{133}$

35. $\frac{39x^4}{80}$

37. $\frac{24}{7y^3}$

39. $− \frac{23y^2}{16}$

41. $\frac{13y^4}{70x^3}$

43. $− \frac{23y^2x^5}{12}$

45. $− \frac{11y^4}{42x^2}$

47. $− \frac{xy}{27}$

49. $\frac{95x^2}{63y}$

51. $\frac{8}{21yx^4}$

53. $\frac{16y}{15x}$

55. $− \frac{68}{7xy^4}$

57. 56 см ²

59. 78 см ²

61. 252 см ²

63. 63 футів ²

65. 30 у ²

67. 10 см ²

69. 23 фунта