4.4: Ділення дробів
- Page ID
- 57344
Припустимо, що у вас чотири піци і кожна з піц була нарізана на вісім рівних скибочок. Тому кожен шматочок піци являє собою 1/8 цілої піци.
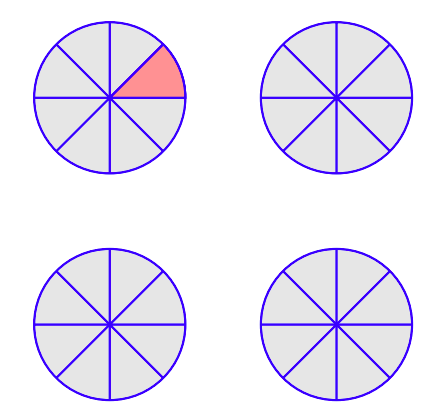
Тепер щодо питання: Скільки восьмих у чотирьох? Це заява про поділ. Щоб дізнатися, скільки восьмих є в 4, розділіть 4 на 1/8. Тобто,
Число одних-восьмих в чотирьох = 4 ÷\(\frac{1}{8}\).
З іншого боку, щоб знайти кількість однієї вісімки в чотирьох, Рисунок\(\PageIndex{1}\) наочно демонструє, що це еквівалентно питанню, скільки шматочків піци є в чотирьох піцах. Оскільки на піцу є 8 скибочок і чотири піци,
Кількість скибочок піци = 4 · 8.
Висновок полягає в тому, що 4 ÷ (1/8) еквівалентно 4 · 8. Тобто,
\[\begin{align*} 4 ÷ 1/8 &= 4 \cdot 8 \\[4pt] &= 32. \end{align*}\]
Тому робимо висновок, що в 4 є 32 восьмих.
Взаємні
Число 1 все ще є мультиплікативною ідентичністю для дробів.
Властивість мультиплікативної ідентичності
Нехай a/b буде будь-який дріб. Потім,
\[ \frac{a}{b} \cdot 1 = \frac{a}{b} \text{ and } 1 \cdot \frac{a}{b} = \frac{a}{b}.\nonumber \]
Число 1 називається мультиплікативною ідентичністю, оскільки однакове число повертається при множенні на 1.
Далі, якщо ми перевертаємо 3/4, тобто якщо перевернемо 3/4 догори дном, то отримаємо 4/3. Зверніть увагу, що відбувається, коли ми множимо 3/4 на 4/3.
Число 4/3 називається мультиплікативним оберненим або зворотним 3/4. Твір взаємних завжди дорівнює 1.
Мультиплікативна обернена властивість
Нехай a/b буде будь-який дріб. Число b/a називається мультиплікативним оберненим або зворотним a/b. Твір зворотних - 1.
\[ \frac{a}{b} \cdot \frac{b}{a} = 1\nonumber \]
Примітка: Щоб знайти мультиплікативне обернене (зворотне) числа, просто інвертуйте число (переверніть його догори дном).
Наприклад, число 1/8 - це мультиплікативний зворотний (зворотний) 8, оскільки
\[ 8 \cdot \frac{1}{8} = 1.\nonumber \]
Зверніть увагу, що 8 можна вважати 8/1. Інвертуйте це число (переверніть його догори дном), щоб знайти його мультиплікативний зворотний (зворотний) 1/8.
Приклад\(\PageIndex{1}\)
Знайти мультиплікативні інверси (взаємні): (a) 2/3, (b) −3/5 та (c) −12.
Рішення
а) Тому що
\[ \frac{2}{3} \cdot \frac{3}{2} = 1,\nonumber \]
мультиплікативний зворотний (зворотний) 2/3 дорівнює 3/2.
б) Тому що
\[ - \frac{3}{5} \cdot \left( - \frac{5}{3} \right) = 1,\nonumber \]
мультиплікативний обернений (зворотний) −3/5 дорівнює −5/3. Знову зауважте, що ми просто перевернули число −3/5, щоб отримати його зворотний −5/3.
в) Тому що
\[ -12 \cdot \left( - \frac{1}{12} \right) = 1, \nonumber \]
мультиплікативний обернений (зворотний) −12 дорівнює −1/12. Знову зауважте, що ми просто перевернули число −12 (яке розуміється рівним −12/1), щоб отримати його зворотний −1/12.
Вправа\(\PageIndex{1}\)
Знайти взаємні числа: (a) −3/7 та (b) 15
- Відповідь
-
(а) −7/3, (б) 1/15
Відділ
Нагадаємо, що ми обчислили число восьмих в чотирьох, виконавши такий розрахунок:
\[ \begin{align*} 4 ÷ \frac{1}{8} &= 4 · 8 \\[4pt] &= 32.\end{align*}\]
Зверніть увагу, як ми перевернули дільник (друге число), потім змінили ділення на множення. Це мотивує наступне визначення поділу.
Визначення поділу
Якщо a/b і c/d - будь-які дроби, то
\[ \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c}.\nonumber \]
Тобто інвертуємо дільник (друге число) і міняємо ділення на множення. Примітка: Ми любимо використовувати фразу «інвертувати та помножити» як допоміжний засіб пам'яті для цього визначення.
Приклад\(\PageIndex{2}\)
Розділіть 1/2 на 3/5.
Рішення
Щоб розділити 1/2 на 3/5, інвертуємо дільник (друге число), потім множимо.
\[ \begin{align*} \frac{1}{2} \div \frac{3}{5} &= \frac{1}{2} \cdot \frac{5}{3} ~ && \textcolor{red}{ \text{ Invert the divisor (second number).}} \\[4pt] &= \frac{5}{6} ~&& \textcolor{red}{ \text{ Multiply.}} \end{align*}\]
Вправа\(\PageIndex{2}\)
Розділити:
\[ \frac{2}{3} \div \frac{10}{3}\nonumber \]
- Відповідь
-
1/5
Приклад\(\PageIndex{3}\)
Спростити такі вирази: (а) 3 ÷\(\frac{2}{3}\) і (б)\(\frac{4}{5}\) ÷ 5.
Рішення
У кожному випадку інвертуйте дільник (друге число), потім множте.
а) Зверніть увагу, що 3 розуміється як 3/1.
\[ \begin{align*} 3 \div \frac{2}{3} &= \frac{3}{1} \cdot \frac{3}{2} ~ && \textcolor{red}{ \text{ Invert the divisor (second number).}} \\[4pt] &= \frac{9}{2} ~ && \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \end{align*} \]
б) Зверніть увагу, що під 5 розуміється 5/1.
\[ \begin{align*} \frac{4}{5} \div 5 &= \frac{4}{5} \cdot \frac{1}{5} ~ && \textcolor{red}{ \text{ Invert the divisor (second number).}} \\[4pt] &= \frac{4}{25} ~ && \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \end{align*}\]
Вправа\(\PageIndex{3}\)
Розділити:
\[ \frac{15}{7} \div 5\nonumber \]
Відповідь
-
\(\frac{3}{7}\)
Після інвертування вам може знадобитися коефіцієнт і скасувати, як ми навчилися робити в розділі 4.2.
Приклад\(\PageIndex{4}\)
Розділіть −6/35 на 33/55.
Рішення
Інвертувати, множити, коефіцієнт і скасувати загальні фактори.
\[ \begin{aligned} - \frac{6}{35} \div \frac{33}{55} = - \frac{6}{35} \cdot \frac{55}{33} ~ & \textcolor{red}{ \text{ Invert the divisor (second number).}} \\ = - \frac{6 \cdot 55}{35 \cdot 33} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ = - \frac{(2 \cdot 3) \cdot (5 \cdot 11)}{(5 \cdot 7) \cdot (3 \cdot 11)} ~ & \textcolor{red}{ \text{ Factor numerators and denominators.}} \\ = - \frac{2 \cdot \cancel{3} \cdot \cancel{5} \cdot \cancel{11}}{ \cancel{5} \cdot 7 \cdot \cancel{3} \cdot \cancel{11}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{2}{7} ~ & \textcolor{red}{ \text{ Remaining factors.}} \end{aligned}\nonumber \]
Відзначимо, що на відміну від знаків видають негативну відповідь.
Вправа\(\PageIndex{4}\)
Розділити:
\[ \frac{6}{15} \div \left( - \frac{42}{35} \right)\nonumber \]
- Відповідь
-
-1/3
Звичайно, ви також можете вибрати множник чисельників і знаменників на місці, а потім скасувати загальні фактори.
Приклад\(\PageIndex{5}\)
Розділити\(−6/x\) на\(−12/x^2\).
Рішення
Інвертувати, факторні чисельники і знаменники, скасувати загальні множники, потім множити.
\[ \begin{align*} - \frac{6}{x} \div \left( - \frac{12}{x^2} \right) &= - \frac{6}{x} \cdot \left( - \frac{x^2}{12} \right) ~ && \textcolor{red}{ \text{ Invert second number.}} \\[4pt] &= - \frac{2 \cdot 3}{x} \cdot - \frac{x \cdot x}{2 \cdot 2 \cdot 3} ~ && \textcolor{red}{ \text{ Factor numerators and denominators.}} \\[4pt] &= - \frac{ \cancel{2} \cdot \cancel{3}}{ \cancel{x}} \cdot - \frac{ \cancel{x} \cdot x}{2 \cdot \cancel{2} \cdot \cancel{3}} ~ && \textcolor{red}{ \text{ Cancel common factors.}} \\[4pt] &= \frac{x}{2} ~ && \textcolor{red}{ \text{ Multiply.}} \end{align*}\]
Зверніть увагу, що подібні знаки дають позитивну відповідь.
Вправа\(\PageIndex{5}\)
Розділити:
\[ - \frac{12}{a} \div \left( - \frac{15}{a^3} \right)\nonumber \]
- Відповідь
-
\[ - \frac{4 a^2}{5}\nonumber \]
Вправи
У вправах 1-16 знайти зворотне заданого числа.
1. −16/5
2. −3/20
3. −17
4. −16
5. 15/16
6. 7/9
7. 30
8. 28
9. −46
10. −50
11. −9/19
12. −4/7
13. 3/17
14. 3/5
15. 11
16. 48
У вправах 17-32 визначте, яке властивість множення зображено заданою ідентичністю.
17. \(\frac{2}{9} \cdot \frac{9}{2} = 1\)
18. \(\frac{12}{19} \cdot \frac{19}{12} = 1\)
19. \( \frac{−19}{12} \cdot 1 = \frac{−19}{12}\)
20. \(\frac{−19}{8} \cdot 1 = \frac{−19}{8}\)
21. \(−6 \cdot \left( − \frac{1}{6} \right) = 1\)
22. \(−19 \cdot \left( − \frac{1}{19} \right) = 1\)
23. \( \frac{−16}{11} \cdot 1 = \frac{−16}{11}\)
24. \(\frac{−7}{6} \cdot 1 = \frac{−7}{6}\)
25. \(− \frac{4}{1} \cdot \left( − \frac{1}{4} \right) = 1\)
26. \(− \frac{9}{10} \cdot \left( − \frac{10}{9} \right) = 1\)
27. \( \frac{8}{1} \cdot 1 = \frac{8}{1}\)
28. \(\frac{13}{15} \cdot 1 = \frac{13}{15}\)
29. \(14 \cdot \frac{1}{14} = 1\)
30. \(4 \cdot \frac{1}{4} = 1\)
31. \( \frac{13}{8} \cdot 1 = \frac{13}{8}\)
32. \(\frac{1}{13} \cdot 1 = \frac{1}{13}\)
У вправах 33-56 розділіть дроби, і спростіть свій результат.
33. \(\frac{8}{23} \div \frac{−6}{11}\)
34. \(\frac{−10}{21} \div \frac{−6}{5}\)
35. \(\frac{18}{19} \div \frac{−16}{23}\)
36. \(\frac{13}{10} \div \frac{17}{18}\)
37. \(\frac{4}{21} \div \frac{−6}{5}\)
38. \(\frac{2}{9} \div \frac{−12}{19}\)
39. \(\frac{−1}{9} \div \frac{8}{3}\)
40. \(\frac{1}{2} \div \frac{−15}{8}\)
41. \(\frac{−21}{11} \div \frac{3}{10}\)
42. \(\frac{7}{24} \div \frac{−23}{2}\)
43. \(\frac{−12}{7} \div \frac{2}{3}\)
44. \(\frac{−9}{16} \div \frac{6}{7}\)
45. \(\frac{2}{19} \div \frac{24}{23}\)
46. \(\frac{7}{3} \div \frac{−10}{21}\)
47. \(\frac{−9}{5} \div \frac{−24}{19}\)
48. \(\frac{14}{17} \div \frac{−22}{21}\)
49. \(\frac{18}{11} \div \frac{14}{9}\)
50. \(\frac{5}{6} \div \frac{20}{19}\)
51. \(\frac{13}{18} \div \frac{4}{9}\)
52. \(\frac{−3}{2} \div \frac{−7}{12}\)
53. \(\frac{11}{2} \div \frac{−21}{10}\)
54. \(\frac{−9}{2} \div \frac{−13}{22}\)
55. \(\frac{3}{10} \div \frac{12}{5}\)
56. \(\frac{−22}{7} \div \frac{−18}{17}\)
У вправах 57-68 розділіть дроби, і спростіть свій результат.
57. \(\frac{20}{17} \div 5\)
58. \(\frac{21}{8} \div 7\)
59. \(−7 \div \frac{21}{20}\)
60. \(−3 \div \frac{12}{17}\)
61. \(\frac{8}{21} \div 2\)
62. \(\frac{−3}{4} \div (−6)\)
63. \(8 \div \frac{−10}{17}\)
64. \(−6 \div \frac{20}{21}\)
65. \(−8 \div \frac{18}{5}\)
66. \(6 \div \frac{−21}{8}\)
67. \(\frac{3}{4} \div (−9)\)
68. \(\frac{2}{9} \div (−8)\)
У вправах 69-80 розділіть дроби, і спростіть свій результат.
69. \(\frac{11x^2}{12} \div \frac{8x^4}{3}\)
70. \(\frac{−4x^2}{3} \div \frac{11x^6}{6}\)
71. \(\frac{17y}{9} \div \frac{10y^6}{3}\)
72. \(\frac{−5y}{12} \div \frac{−3y^5}{2}\)
73. \(\frac{−22x^4}{13} \div \frac{12x}{11}\)
74. \(\frac{−9y^6}{4} \div \frac{24y^5}{13}\)
75. \(\frac{−3x^4}{10} \div \frac{−4x}{5}\)
76. \(\frac{18y^4}{11} \div \frac{4y^2}{7}\)
77. \(\frac{−15y^2}{14} \div \frac{−10y^5}{13}\)
78. \(\frac{3x}{20} \div \frac{2x^3}{5}\)
79. \(\frac{−15x^5}{13} \div \frac{20x^2}{19}\)
80. \(\frac{18y^6}{7} \div \frac{14y^4}{9}\)
У вправах 81-96 розділіть дроби, і спростіть свій результат.
81. \(\frac{11y^4}{14x^2} \div \frac{−9y^2}{7x^3}\)
82. \(\frac{−5x^2}{12y^3} \div \frac{−22x}{21y^5}\)
83. \(\frac{10x^4}{3y^4} \div \frac{7x^5}{24y^2}\)
84. \(\frac{20x^3}{11y^5} \div \frac{5x^5}{6y^3}\)
85. \(\frac{22y^4}{21x^5} \div \frac{−5y^2}{6x^4}\)
86. \(\frac{−7y^5}{8x^6} \div \frac{21y}{5x^5}\)
87. \(\frac{−22x^4}{21y^3} \div \frac{−17x^3}{3y^4}\)
88. \(\frac{−7y^4}{4x} \div \frac{−15y}{22x^4}\)
89. \(\frac{−16y^2}{3x^3} \div \frac{2y^6}{11x^5}\)
90. \(\frac{−20x}{21y^2} \div \frac{−22x^5}{y^6}\)
91. \(\frac{−x}{12y^4} \div \frac{−23x^3}{16y^3}\)
92. \(\frac{20x^2}{17y^3} \div \frac{8x^3}{15y}\)
93. \(\frac{y^2}{4x} \div \frac{−9y^5}{8x^3}\)
94. \(\frac{−10y^4}{13x^2} \div \frac{−5y^6}{6x^3}\)
95. \(\frac{−18x^6}{13y^4} \div \frac{3x}{y^2}\)
96. \(\frac{20x^4}{9y^6} \div \frac{14x^2}{17y^4}\)
Відповіді
1. \(− \frac{5}{16}\)
3. \(− \frac{1}{17}\)
5. \(\frac{16}{15}\)
7. \(\frac{1}{30}\)
9. \(− \frac{1}{46}\)
11. \(− \frac{19}{9}\)
13. \(\frac{17}{3}\)
15. \(\frac{1}{11}\)
17. мультиплікативна обернена властивість
19. мультиплікативна властивість ідентичності
21. мультиплікативна обернена властивість
23. мультиплікативна властивість ідентичності
25. мультиплікативна обернена властивість
27. мультиплікативна властивість ідентичності
29. мультиплікативне обернене властивість
31. мультиплікативна властивість ідентичності
33. \(− \frac{44}{69}\)
35. \(− \frac{207}{152}\)
37. \(− \frac{10}{63}\)
39. \(− \frac{1}{24}\)
41. \(− \frac{70}{11}\)
43. \(− \frac{18}{7}\)
45. \( \frac{23}{228}\)
47. \( \frac{57}{40}\)
49. \(\frac{81}{77}\)
51. \(\frac{13}{8}\)
53. \(− \frac{55}{21}\)
55. \(\frac{1}{8}\)
57. \(\frac{4}{17}\)
59. \(− \frac{20}{3}\)
61. \(\frac{4}{21}\)
63. \(− \frac{68}{5}\)
65. \(− \frac{20}{9}\)
67. \(− \frac{1}{12}\)
69. \(\frac{11}{32x^2}\)
71. \(\frac{17}{30y^5}\)
73. \(− \frac{121x^3}{78}\)
75. \(\frac{3x^3}{8}\)
77. \( \frac{39}{28y^3}\)
79. \(− \frac{57x^3}{52}\)
81. \(− \frac{11y^2x}{18}\)
83. \(\frac{80}{7xy^2}\)
85. \(− \frac{44y^2}{35x}\)
87. \(\frac{22xy}{119}\)
89. \(− \frac{88x^2}{3y^4}\)
91. \(\frac{4}{69x^2y}\)
93. \(− \frac{2x^2}{9y^3}\)
95. \(− \frac{6x^5}{13y^2}\)
