Skip to main content
LibreTexts - Ukrayinska

4.8: Порядок операцій з дробами

  1. Last updated
  2. Save as PDF
  • Page ID
    57350

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Почнемо з прийняття повноважень дробів. Нагадаємо, що

    \[ a^m = \underbrace{a \cdot a \cdot ... \cdot a}_{m \text{ times}}\nonumber \]

    Приклад 1

    Спростити: (−3/4) 2.

    Рішення

    За визначенням,

    \[ \begin{aligned} \left( - \frac{3}{4} \right)^2 = \left( - \frac{3}{4} \right) \left( - \frac{3}{4} \right) ~& \textcolor{red}{ \text{ Fact: } a^2 = a \cdot a.} \\ = \frac{3 \cdot 3}{4 \cdot 4} ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply numerators and denominators.} \\ \text{ Product of even number of negative factors is positive.} \end{array}} \\ = \frac{9}{16} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

    Вправа

    Спростити:

    \[ \left( - \frac{2}{5} \right)^2\nonumber \]

    Відповідь

    4/25

    Приклад 2

    Спростити: (−2/3) 3.

    Рішення

    За визначенням,

    \[ \begin{aligned} \left( - \frac{2}{3}\right)^3 = \left( - \frac{2}{3} \right) \left( - \frac{2}{3} \right) \left( - \frac{2}{3} \right) ~ & \textcolor{red}{ \text{ Fact: } a^3 = a \cdot a \cdot a.} \\ = - \frac{2 \cdot 2 \cdot 2}{3 \cdot 3 \cdot 3} ~ & \textcolor{red}{ \begin{array} ~ \text{ Multiply numerators and denominators.} \\ \text{ Product of odd number of negative factors is negative.} \end{array}} \\ = - \frac{8}{27} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

    Вправа

    Спростити:

    \[ \left( - \frac{1}{6} \right)^3\nonumber \]

    Відповідь

    −1/216

    Останні два приклади повторюють принцип, засвоєний раніше.

    Непарні і парні

    • Твір парного ряду негативних факторів позитивний.
    • Твір непарного числа негативних чинників - негативний.

    Порядок операцій

    Для зручності повторюємо тут правила, що керують порядком операцій.

    Правила, що керують порядком операцій

    При оцінці виразів дійте в наступному порядку.

    1. Спочатку оцініть вирази, що містяться в символах групування. Якщо символи групування вкладені, спочатку оцініть вираз у внутрішній парі символів групування.
    2. Оцінити всі експоненти, які з'являються у виразі.
    3. Виконуйте всі множення і ділення в тому порядку, щоб вони відображалися у виразі, рухаючись зліва направо.
    4. Виконуйте всі додавання і віднімання в тому порядку, щоб вони відображалися у виразі, рухаючись зліва направо.

    Приклад 3

    Спростити:\(- \frac{1}{2} + \frac{1}{4} \left( - \frac{1}{3} \right)\).

    Рішення

    Спочатку помножте, потім додайте.

    \[ \begin{aligned} - \frac{1}{2} + \frac{1}{4} \left( - \frac{1}{3} \right) = - \frac{1}{2} + \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \text{ Multiply: } \frac{1}{4} \left( - \frac{1}{3} \right) = - \frac{1}{12}.} \\ = - \frac{1 \cdot \textcolor{red}{6}}{2 \cdot \textcolor{red}{6}} + \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 12.}} \\ = - \frac{6}{12} + \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = - \frac{7}{12} ~ & \textcolor{red}{ \text{ Add over common denominator.}} \end{aligned}\nonumber \]

    Вправа

    Спростити:\( - \frac{2}{3} + \frac{3}{4} \left( - \frac{1}{2} \right)\)

    Відповідь

    −25/24

    Приклад 4

    Спростити:\(2 \left( - \frac{1}{2} \right)^2 +4 \left( - \frac{1}{2} \right)\).

    Рішення

    Показники спочатку, потім множать, потім складають.

    \[ \begin{aligned} 2 \left( - \frac{1}{2} \right)^2 + 4 \left( - \frac{1}{2} \right) = 2 \left( \frac{1}{4} \right) + 4 \left( - \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ Exponent first: } \left( - \frac{1}{2} \right)^2 = \frac{1}{4}.} \\ = \frac{1}{2} + \left( - \frac{2}{1} \right) ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply: } 2 \left( \frac{1}{4} \right) = \frac{1}{2} \\ \text{ and } 4 \left( - \frac{1}{2} \right) = - \frac{2}{1}. \end{array}} \\ = \frac{1}{2} + \left( - \frac{2 \cdot \textcolor{red}{2}}{1 \cdot \textcolor{red}{2}} \right) ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 2.}} \\ = \frac{1}{2} + \left( - \frac{4}{2} \right) ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = - \frac{3}{2} ~ & \textcolor{red}{ \text{ Add over common denominator.}} \end{aligned}\nonumber \]

    Вправа

    Спростити:\(3 \left( - \frac{1}{3} \right)^2 - 2 \left( - \frac{1}{3} \right)\)

    Відповідь

    1

    Приклад 5

    За даними a = −3/4, b = 1/2, c = 1/3 та d = −1/4, оцініть вираз ab − cd.

    Рішення

    Нагадаємо, що гарною практикою є підготовка дужок перед заміною.

    \[ ad - bc = ( ~ ) (~) - (~)(~)\nonumber \]

    Підставляємо задані значення в алгебраїчний вираз, а потім спрощуємо за допомогою порядку операцій.

    \[ \begin{aligned} ab - cd = \left( - \frac{3}{4} \right) \left( \frac{1}{2} \right) - \left( \frac{1}{3} \right) \left( - \frac{1}{4} \right) ~ & \textcolor{red}{ \begin{array}{l} \text{ Substitute: } -3/4 \text{ for } a, ~ 1/2 \text{ for } b, \\ 1/3 \text{ for } c, ~ \text{ and } -1/4 \text{ for } d. \end{array}} \\ = - \frac{3}{8} - \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply first: } \left( - \frac{3}{4} \right) \left( \frac{1}{2} \right) = - \frac{3}{8} \\ \text{ and } \left( \frac{1}{3} \right) \left( - \frac{1}{4} \right) = - \frac{1}{12}. \end{array}} \\ = - \frac{3}{8} + \frac{1}{12} ~ & \textcolor{red}{ \text{ Subtract by adding opposite.}} \\ = - \frac{3 \cdot \textcolor{red}{3}}{8 \cdot \textcolor{red}{3}} + \frac{1 \cdot \textcolor{red}{2}}{12 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions; LCD = 24.}} \\ = - \frac{9}{24} + \frac{2}{24} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = - \frac{7}{24} ~ & \textcolor{red}{ \text{ Add over common denominator.}} \end{aligned}\nonumber \]

    Вправа

    Враховуючи a = −1/2, b = 1/3, а c = −1/5, оцініть a + bc.

    Відповідь

    −17/30

    Приклад 6

    З огляду на a = −1/4 і b = 1/2, обчислити (a 2 − b 2) ÷ (a+ b).

    Рішення

    Нагадаємо, що гарною практикою є підготовка дужок перед заміною.

    \[ (a^2 - b^2 ) \div (a+b) - \left( (~)^2 - (~)^2 \right) \div \left( (~) + (~) \right)\nonumber \]

    Підставляємо задані значення в алгебраїчний вираз, потім спочатку оцінюємо показники.

    \[ \begin{array}{l} (a^2 -b^2) \div (a+b) & = \left( \left( - \frac{1}{4} \right)^2 - \left( \frac{1}{2} \right)^2 \right) \div \left( \left( - \frac{1}{4} \right) + \left( \frac{1}{2} \right) \right) \\ ~ & = \left( \frac{1}{16} - \frac{1}{4} \right) \div \left( - \frac{1}{4} + \frac{1}{2} \right) \end{array}\nonumber \]

    Ми повинні спочатку оцінити дужки. Усередині кожного набору дужок створіть еквівалентні дроби і виконайте віднімання і додавання далі.

    \[ \begin{array}{l} = \left( \frac{1}{16} - \frac{1 \cdot 4}{4 \cdot 4} \right) \div \left( - \frac{1}{4} + \frac{1 \cdot 2}{2 \cdot 2} \right) \\ = \left( \frac{1}{16} - \frac{4}{16} \right) \div \left( - \frac{1}{4} + \frac{2}{4} \right) \\ = - \frac{3}{16} \div \frac{1}{4} \end{array}\nonumber \]

    Інвертувати і перемножити.

    \[ \begin{aligned} = - \frac{3}{16} \cdot \frac{4}{1} \\ = - \frac{12}{16} \end{aligned}\nonumber \]

    Зменшити.

    \[ \begin{aligned} = - \frac{12 \div 4}{16 \div 4} \\ - \frac{3}{4} \end{aligned}\nonumber \]

    Примітка: На останньому кроці ви також можете зменшити за допомогою простого факторингу чисельника та знаменника та скасування загальних факторів.

    Вправа

    Дайте a = −1/2 і b = −1/3, оцініть ab ÷ (a + b).

    Відповідь

    −1/5

    Складні дроби

    Складні дроби

    Коли чисельник і знаменник дробу містять самі дроби, такий вираз називається складним дробом.

    Ви можете використовувати стандартний порядок операцій для спрощення складного дробу. Згадайте пораду, коли присутній дріб.

    Дробові вирази

    Якщо присутній дробовий вираз, спростіть чисельник і знаменник окремо, потім діліть.

    Приклад 7

    Спростити:

    \[ \frac{ - \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}}\nonumber \]

    Рішення

    У нас є додавання в чисельнику, віднімання в знаменнику. У кожному конкретному випадку потрібні еквівалентні дроби із загальним знаменником.

    \[ \begin{aligned} \frac{- \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}} = \frac{- \frac{1 \cdot \textcolor{red}{3}}{2 \cdot \textcolor{red}{3}} + \frac{1 \cdot \textcolor{red}{2}}{3 \cdot \textcolor{red}{2}}} ~ & \textcolor{red}{ \text{ Create equivalent fractions.}} \\ = \frac{- \frac{3}{6} + \frac{2}{6}}{ \frac{3}{4} - \frac{6}{4}} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = \frac{- \frac{1}{6}}{- \frac{3}{4}} ~ & \textcolor{red}{ \begin{array}{l} ~ \text{ Numerator: } - \frac{3}{6} + \frac{2}{6} = - \frac{1}{6}. \\ \text{ Denominator: } \frac{3}{4} - \frac{6}{4} = - \frac{3}{4}. \end{array}} \end{aligned}\nonumber \]

    Останній вислів просить нас розділити. Інвертувати і перемножити.

    \[ \begin{aligned} = - \frac{1}{6} \div \left( - \frac{3}{4} \right) ~ & \textcolor{red}{ \text{ A complex fraction means divide.}} \\ = - \frac{1}{6} \cdot \left( - \frac{4}{3} \right) ~ & \textcolor{red}{ \text{ Invert and multiply.}} \end{aligned}\nonumber \]

    Подібні знаки (два негативу) дають позитивний продукт. Множимо чисельники і знаменники, потім зменшуємо.

    \[ \begin{aligned} = \frac{4}{18} ~ & \textcolor{red}{ \begin{array}{l} \text{ Like signs yields positive answer.} \\ \text{ Multiply numerators and denominators.} \end{array}} \\ = \frac{4 \div 2}{18 \div 2} ~ & \textcolor{red}{ \text{ Divide both numerator and denominator by 2.}} \\ = \frac{2}{9} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

    Крім того, можна просте множник і скасувати, щоб зменшити до найнижчих термінів; тобто

    \[ \begin{aligned} \frac{4}{18} = \frac{2 \cdot 2}{2\cdot 3 \cdot 3} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = \frac{ \cancel{2} \cdot 2}{ \cancel{2} \cdot 3 \cdot 3} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{2}{9} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

    Вправа

    Спростити:

    \[ \frac{ \frac{1}{4} - \frac{1}{3}}{ \frac{1}{4} + \frac{1}{3}}\nonumber \]

    Відповідь

    −1/7

    Очищення дробів

    Доступна альтернативна методика спрощення складних дробів.

    Очищення дробів від складних дробів

    Очистити дроби зі складного дробу можна за допомогою наступного алгоритму:

    1. Визначте LCD1 для чисельника.
    2. Визначте LCD2 для знаменника.
    3. Визначте РК-дисплей як для LCD1, так і для LCD2.
    4. Помножте чисельник і знаменник на цей «комбінований» РК-дисплей.

    Давайте застосуємо цю техніку до складного дробу Прикладу 7.

    Приклад 8

    Спростити:

    \[ \frac{- \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}}\nonumber \]

    Рішення

    Як ми бачили в рішенні в прикладі 7, спільні знаменники 6 і 4 використовувалися для чисельника і знаменника відповідно. Таким чином, спільним знаменником як для чисельника, так і для знаменника буде 12. Почнемо техніку альтернативного розв'язку з множення чисельника і знаменника на 12.

    \[ \begin{aligned} \frac{ - \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}} = \frac{ \textcolor{red}{12} \left( - \frac{1}{2} + \frac{1}{3} \right)}{ \textcolor{red}{12} \left( \frac{3}{4} - \frac{3}{2} \right)} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 12.}} \\ = \frac{ \textcolor{red}{12} \left( - \frac{1}{2} \right) + \textcolor{red}{12} \left( \frac{1}{3} \right)}{ \textcolor{red}{12} \left( \frac{3}{4} \right) - \textcolor{red}{12} \left( \frac{3}{2} \right)} ~ & \textcolor{red}{ \text{ Distribute the 12.}} \\ = \frac{-6+4}{9-18} ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply: } 12(-1/2)=-6,~ 12(1/2) = 4. \\ 12(3/4)=9, \text{ and } 12(3/2)=18. \end{array}} \\ = \frac{-2}{-9} ~ & \textcolor{red}{ \text{ Simplify.}} \\ = \frac{2}{9} ~ & \textcolor{red}{ \text{ Like signs yield positive.}} \end{aligned}\nonumber \]

    Вправа

    Спростити:\( \frac{- \frac{2}{3} + \frac{1}{5}}{ \frac{4}{5} - \frac{1}{2}}\)

    Відповідь

    −14/9

    Застосування — Трапеція

    Трапеція - це особливий тип чотирикутника (чотиригранний багатокутник).

    Трапеція

    Чотирикутник з однією парою паралельних протилежних сторін називається трапецією.

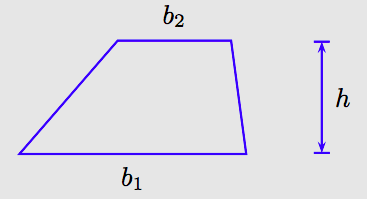
    Знімок екрана 2019-09-04 в 4.20.28 PM.png

    Пару паралельних сторін називають підставами трапеції. Їх довжини відзначаються змінними b 1 і b 2 на малюнку вище. Відстань між паралельними підставами називається висотою або висотою трапеції. Висота відзначається змінною h на малюнку вище.

    Математики використовують індекси для створення нових змінних. Таким чином, b 1 («b sub 1») і b 2 («b sub 2») є двома різними змінними, що використовуються в даному випадку для представлення довжини підстав трапеції.

    Малюючи по діагоналі, ми можемо розділити трапецію на два трикутника (див. Рис.

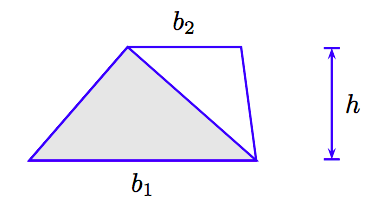
    Знімок екрана 2019-09-04 в 4.20.54 PM.png
    Малюнок 4.14: Розділення трапеції на два трикутника.

    Ми можемо знайти площу трапеції, підсумовуючи площі двох трикутників.

    • Затінений трикутник на малюнку 4.14 має підставу b 1 і висоту h. Значить, площа затіненого трикутника дорівнює (1/2) b 1 h.
    • Незатінений трикутник на малюнку 4.14 має підставу b 2 і висоту h. Значить, площа незаштрихованого трикутника дорівнює (1/2) b 2 h.

    Підсумовуючи площі, площа трапеції дорівнює

    \[ \text{Area of Trapezoid} = \frac{1}{2} b_1h + \frac{1}{2} b_2h.\nonumber \]

    Ми можемо використовувати розподільну властивість для коефіцієнта a (1/2) h.

    Площа трапеції

    Трапеція з підставами b 1 і b 2 і висотою h має площу.

    \[A = \frac{1}{2} h (b_1 + b_2).\nonumber \]

    Тобто, щоб знайти площу, підсумувати підстави, помножити на висоту, і взяти половину результату.

    Приклад 9

    Знайдіть площу трапеції на фото нижче.

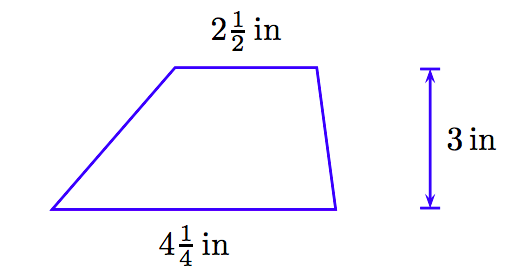
    Знімок екрана 2019-09-04 в 4.25.28 PM.png

    Рішення

    Формула для площі трапеції така

    \[A = \frac{1}{2} h (b_1 + b_2)\nonumber \]

    Підставивши задані підстави і висоту, отримуємо

    \[A = \frac{1}{2} (3) \left( 4 \frac{1}{4} + 2 \frac{1}{2} \right).\nonumber \]

    Спочатку спростіть вираз всередині дужок. Змішайте змішані дроби на неправильні дроби, зробіть еквівалентні дроби із загальним знаменником, потім додайте.

    \[\begin{array}{c} A = \frac{1}{2} (3) \left( \frac{17}{4} + \frac{5}{2} \right) \\ = \frac{1}{2} (3) \left( \frac{17}{4} + \frac{5 \cdot 2}{2 \cdot 2} \right) \\ = \frac{1}{2} (3) \left( \frac{17}{4} + \frac{10}{4} \right) \\ = \frac{1}{2} \left( \frac{3}{1} \right) \left( \frac{27}{4} \right) \end{array}\nonumber \]

    Множимо чисельники і знаменники.

    \[ = \frac{81}{8}\nonumber \]

    Ця неправильна дріб - цілком хороша відповідь, але давайте змінимо цей результат на змішаний дріб (81 поділений на 8 дорівнює 10 із залишком 1). Таким чином, площа трапеції дорівнює

    \[A = 10 \frac{1}{8} \text{ square inches.}\nonumber \]

    Вправа

    Трапеція має підстави розміром 6 і 15 футів відповідно. Висота трапеції - 5 футів. Знайдіть площу трапеції.

    Відповідь

    \(52 \frac{1}{2} \text{ square feet}\)

    Вправи

    У вправах 1-8 спростіть вираз.

    1. \( \left( − \frac{7}{3} \right)^3\)

    2. \( \left( \frac{1}{2} \right)^3\)

    3. \( \left( \frac{5}{3} \right)^4\)

    4. \( \left( − \frac{3}{5} \right)^4\)

    5. \( \left( \frac{1}{2} \right)^5\)

    6. \( \left( \frac{3}{4} \right)^5\)

    7. \( \left( \frac{4}{3} \right)^2\)

    8. \( \left( − \frac{8}{5} \right)^2\)

    9. Якщо a = 7/6, оцініть 3.

    10. Якщо e = 1/6, оцініть е 3.

    11. Якщо e = −2/3, оцініть − e 2.

    12. Якщо c = −1/5, оцініть − c 2.

    13. Якщо b = −5/9, оцініть b 2.

    14. Якщо c = 5/7, оцініть c 2.

    15. Якщо b = −1/2, оцініть − b 3.

    16. Якщо a = −2/9, оцініть − a 3.

    У вправах 17-36 спростіть вираз.

    17. \( \left( − \frac{1}{2} \right) \left( \frac{1}{6} \right) − \left( \frac{7}{8} \right) \left( − \frac{7}{9} \right)\)

    18. \( \left( − \frac{3}{4} \right) \left( \frac{1}{2} \right) − \left( \frac{3}{5} \right) \left( \frac{1}{4} \right)\)

    19. \( \left( − \frac{9}{8} \right)^2 − \left( − \frac{3}{2} \right) \left( \frac{7}{3} \right)\)

    20. \( \left( \frac{3}{2} \right)^2 − \left( \frac{7}{8} \right) \left( − \frac{1}{2} \right)\)

    21. \( \left( − \frac{1}{2} \right) \left( − \frac{7}{4} \right) − \left( − \frac{1}{2} \right)^2\)

    22. \( \left( \frac{1}{5} \right) \left( − \frac{9}{4} \right) − \left( \frac{7}{4} \right)^2\)

    23. \(− \frac{7}{6} − \frac{1}{7} \cdot \frac{7}{9}\)

    24. \( − \frac{4}{9} − \frac{8}{5} \cdot \frac{8}{9}\)

    25. \( \frac{3}{4} + \frac{9}{7} \left( − \frac{7}{6} \right)\)

    26. \( \frac{3}{2} + \frac{1}{4} \left( − \frac{9}{8} \right)\)

    27. \( \left( − \frac{1}{3} \right)^2 + \left( \frac{7}{8} \right) \left( − \frac{1}{3} \right)\)

    28. \( \left( − \frac{2}{9} \right)^2 + \left( \frac{2}{3} \right) \left( \frac{1}{2} \right)\)

    29. \(\frac{5}{9} + \frac{5}{9} \cdot \frac{7}{9}\)

    30. \( − \frac{1}{2} + \frac{9}{8} \cdot \frac{1}{3}\)

    31. \( \left( − \frac{5}{6} \right) \left( \frac{3}{8} \right) + \left( − \frac{7}{9} \right) \left( − \frac{3}{4} \right)\)

    32. \( \left( \frac{7}{4} \right) \left( \frac{6}{5} \right) + \left( − \frac{2}{5} \right) \left( \frac{8}{3} \right)\)

    33. \( \frac{4}{3} − \frac{2}{9} \left( − \frac{3}{4} \right)\)

    34. \(− \frac{1}{3} − \frac{1}{5} \left( − \frac{4}{3} \right)\)

    35. \( \left( − \frac{5}{9} \right) \left( \frac{1}{2} \right) + \left( − \frac{1}{6} \right)^2\)

    36. \( \left( \frac{1}{4} \right) \left( \frac{1}{6} \right) + \left( − \frac{5}{6} \right)^2\)

    37. Враховуючи a = −5/4, b = 1/2, а c = 3/8, оцініть a + bc.

    38. Враховуючи a = −3/5, b = 1/5, а c = 1/3, оцініть a + bc.

    39. Задано x = −1/8, y = 5/2, а z = −1/2, обчислити вираз x + yz.

    40. Задано x = −5/9, y = 1/4, а z = −2/3, обчислити вираз x + yz.

    41. Задано a = 3/4, b = 5/7 і c = 1/2, оцініть вираз a − bc.

    42. Задано a = 5/9, b = 2/3, а c = 2/9, оцініть вираз a − bc.

    43. За даними x = −3/2, y = 1/4, а z = −5/7, оцініть x 2 − yz.

    44. За даними x = −3/2, y = −1/2, а z = 5/3, оцініть x 2 − yz.

    45. Враховуючи a = 6/7, b = 2/3, c = −8/9, а d = −6/7, оцініть ab + cd.

    46. Враховуючи a = 4/9, b = −3/2, c = 7/3, а d = −8/9, оцініть ab + cd.

    47. Враховуючи w = −1/8, x = −2/7, y = −1/2 та z = 8/7, оцініть wx − yz.

    48. Враховуючи w = 2/7, x = −9/4, y = −3/4, а z = −9/2, оцініть wx − yz.

    49. Враховуючи x = 3/8, y = 3/5, а z = −3/2, оцініть xy+ z 2.

    50. Враховуючи x = −1/2, y = 7/5, а z = −3/2, оцініть xy+ z 2.

    51. Враховуючи u = 9/7, v = 2/3, а w = −3/7, оцініть uv − w 2.

    52. Враховуючи u = 8/7, v = −4/3, а w = 2/3, оцініть uv − w 2.

    53. Враховуючи a = 7/8, b = −1/4, а c = −3/2, оцініть a 2 + bc.

    54. Враховуючи a = −5/8, b = 3/2, а c = −3/2, оцініть a 2 + bc.

    55. Задано u = 1/3, v = 5/2, а w = −2/9, обчислити вираз u − vw.

    56. Задано u = −1/2, v = 1/4, а w = −1/4, обчислити вираз u − vw.

    У вправах 57-68 спростити складне раціональне вираження.

    57. \(\frac{ \frac{8}{3} + \frac{7}{6}}{− \frac{9}{2} − \frac{1}{4}}\)

    58. \( \frac{ \frac{7}{8} + \frac{1}{9}}{ \frac{8}{9} − \frac{1}{6}}\)

    59. \( \frac{ \frac{3}{4} + \frac{4}{3}}{ \frac{1}{9} + \frac{5}{3}}\)

    60. \( \frac{− \frac{9}{8} − \frac{6}{5}}{ \frac{7}{4} + \frac{1}{2}}\)

    61. \( \frac{ \frac{7}{5} + \frac{5}{2}}{− \frac{1}{4} + \frac{1}{2}}\)

    62. \( \frac{ \frac{5}{6} + \frac{2}{3}}{ \frac{3}{5} + \frac{2}{3}}\)

    63. \( \frac{− \frac{3}{2} − \frac{2}{3}}{− \frac{7}{4} − \frac{2}{3}}\)

    64. \( \frac{ \frac{8}{9} + \frac{3}{4}}{− \frac{2}{3} − \frac{1}{6}}\)

    65. \( \frac{− \frac{1}{2} − \frac{4}{7}}{− \frac{5}{7} + \frac{1}{6}}\)

    66. \( \frac{− \frac{3}{2} − \frac{5}{8}}{ \frac{3}{4} − \frac{1}{2}}\)

    67. \(\frac{− \frac{3}{7} − \frac{1}{3}}{ \frac{1}{3} − \frac{6}{7}}\)

    68. \( \frac{− \frac{5}{8} − \frac{6}{5}}{− \frac{5}{4} − \frac{3}{8}}\)

    69. Трапеція має\(3 \frac{3}{8}\) підстави вимірювальні і\(5 \frac{1}{2}\) ніжки відповідно. Висота трапеції - 7 футів. Знайдіть площу трапеції.

    70. Трапеція має\(2 \frac{1}{2}\) підстави вимірювальні і\(6 \frac{7}{8}\) ніжки відповідно. Висота трапеції - 3 фути. Знайдіть площу трапеції.

    71. Трапеція має\(2 \frac{1}{4}\) підстави вимірювальні і\(7 \frac{3}{8}\) ніжки відповідно. Висота трапеції - 7 футів. Знайдіть площу трапеції.

    72. Трапеція має\(3 \frac{1}{8}\) підстави вимірювальні і\(6 \frac{1}{2}\) ніжки відповідно. Висота трапеції - 3 фути. Знайдіть площу трапеції.

    73. Трапеція має\(2 \frac{3}{4}\) підстави вимірювальні і\(6 \frac{5}{8}\) ніжки відповідно. Висота трапеції - 3 фути. Знайдіть площу трапеції.

    74. Трапеція має\(2 \frac{1}{4}\) підстави вимірювальні і\(7 \frac{1}{8}\) ніжки відповідно. Висота трапеції - 5 футів. Знайдіть площу трапеції.

    Відповіді

    1. \(\frac{−343}{27}\)

    3. \(\frac{625}{81}\)

    5. \(\frac{1}{32}\)

    7. \(\frac{16}{9}\)

    9. \(\frac{343}{216}\)

    11. \(\frac{−4}{9}\)

    13. \(\frac{25}{81}\)

    15. \(\frac{1}{8}\)

    17. \(\frac{43}{72}\)

    19. \(\frac{305}{64}\)

    21. \(\frac{5}{8}\)

    23. \(\frac{−23}{18}\)

    25. \(\frac{−3}{4}\)

    27. \(\frac{−13}{72}\)

    29. \(\frac{80}{81}\)

    31. \(\frac{13}{48}\)

    33. \(\frac{3}{2}\)

    35. \(\frac{−1}{4}\)

    37. \(\frac{−17}{16}\)

    39. \(\frac{−11}{8}\)

    41. \(\frac{11}{28}\)

    43. \(\frac{17}{7}\)

    45. \(\frac{4}{3}\)

    47. \(\frac{17}{28}\)

    49. \(\frac{99}{40}\)

    51. \(\frac{33}{49}\)

    53. \(\frac{73}{64}\)

    55. \(\frac{8}{9}\)

    57. \(\frac{−46}{57}\)

    59. \(\frac{75}{64}\)

    61. \(\frac{78}{5}\)

    63. \(\frac{26}{29}\)

    65. \(\frac{45}{23}\)

    67. \(\frac{16}{11}\)

    69. \(31 \frac{1}{16}\)

    71. \(33 \frac{11}{16}\)

    73. \(14 \frac{1}{16}\)