4.2: Еквівалентні дроби
- Page ID
- 57373
У цьому розділі ми маємо справу з дробами, числами або виразами виду a/b.
Визначення: Дроби
Номер форми
\[ \dfrac{a}{b}\nonumber \]
де\(a\) і\(b\) є числа називається дробом. Число\(a\) називається чисельником дробу, тоді як число\(b\) називається знаменником дробу.
Ближче до кінця цього розділу ми побачимо, що чисельник і знаменник дробу також можуть бути алгебраїчними виразами, але на даний момент ми обмежимо нашу увагу дробами, чиї чисельники і знаменники є цілими числами. Почнемо наше дослідження дробів з визначення еквівалентних дробів.
Еквівалентні дроби
Два дроби еквівалентні, якщо вони представляють одне і те ж числове значення.
Але як ми можемо визначити, якщо два дроби представляють одне і те ж число? Ну, одна техніка передбачає кілька простих візуалізацій. Розглянемо зображення, показане на малюнку 4.1, де затінена область становить 1/3 загальної площі фігури (одна з трьох рівних областей затінена).

На малюнку 4.2 ми затінювали 2/6 всієї області (дві з шести рівних областей затінені).

На малюнку 4.3 ми затінювали 4/12 всієї області (чотири з дванадцяти рівних областей затінені).
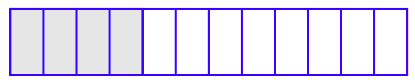
Візьмемо схеми з малюнка 4.1, рис. 4.2, і рис. 4.3 і складемо їх один поверх іншого, як показано на малюнку 4.4.
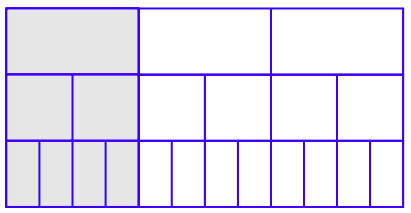
На малюнку 4.4 наведено тверді візуальні докази того, що наступні дроби еквівалентні.
\[ \dfrac{1}{3} = \dfrac{2}{6} = \dfrac{4}{12}\nonumber \]
Ключові спостереження
1. Якщо почати з дробу 1/3, то помножити і чисельник і знаменник на 2, отримаємо наступний результат.
\[ \begin{aligned} \dfrac{1}{3} = \dfrac{1 \cdot 2}{3 \cdot 2} ~ & \textcolor{red}{ \text{ Multiply the numerator and denominator by 2.}} \\ = \dfrac{2}{6} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Це саме те саме, що відбувається з малюнка 4.1 до 4.2, де ми подвоюємо кількість доступних коробок (від 3 доступних до 6 доступних) і подвоюємо кількість затінених коробок (від 1 затінених до 2 затінених).
2. Якщо почати з дробу 1/3, то помножити і чисельник і знаменник на 4, отримаємо наступний результат.
\[ \begin{aligned} = \dfrac{1}{3} = \dfrac{1 \cdot 4}{3 \cdot 4} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 4.}} \\ = \dfrac{4}{12} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Це саме те саме, що відбувається з малюнка 4.1 до 4.3, де ми множимо кількість доступних коробок на 4 (від 3 доступних до 12 доступних) і множимо кількість затінених коробок на 4 (від 1 затінених до 4 затінених).
Вищевикладене обговорення мотивує наступний фундаментальний результат.
Створення еквівалентних дробів
Якщо почати з дробу, то помножити і його чисельник і знаменник на одне і те ж число, отриманий дріб еквівалентний (має однакове числове значення) вихідному дробу. В символах,
\[ \dfrac{a}{b} = \dfrac{a \cdot x}{b \cdot x}\nonumber \]
Сперечаючись у зворотному напрямку
Повернення вищевказаного аргументу також має значення true.
1. Якщо почати з дробу 2/6, то розділити і чисельник і знаменник на 2, отримаємо наступний результат.
\[ \begin{aligned} \dfrac{2}{6} = \dfrac{2 \div 2}{6 \div 2} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 2.}} \\ = \dfrac{1}{3} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Це саме те саме, що відбувається назад від малюнка 4.2 до 4.1, де ми ділимо кількість доступних коробок на 2 (від 6 доступних до 3 доступних) і ділимо кількість затінених коробок на 2 (від 2 затінених до 1 затінених).
2. Якщо почати з дробу 4/12, то розділити і чисельник і знаменник на 4, отримаємо наступний результат.
\[ \begin{aligned} \dfrac{4}{12} = \dfrac{4 \div 4}{12 \div 4} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 4.}} \\ = \dfrac{1}{3} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Це саме те саме, що відбувається назад від малюнка 4.3 до 4.1, де ми ділимо кількість доступних коробок на 4 (переходячи від 12 доступних до 3 доступних) і ділимо кількість alignof затінених коробок на 4 (переходячи від 4 затінених до 1 затінених).
Вищевикладене обговорення мотивує наступний фундаментальний результат.
Створення еквівалентних дробів
Якщо почати з дробу, то розділити і його чисельник, і знаменник на одне і те ж число, отриманий дріб еквівалентний (має однакове числове значення) вихідному дробу. В символах,
\[ \dfrac{a}{b} = \dfrac{a \div x}{b \div x}.\nonumber \]
Найбільший спільний дільник
Нам потрібно трохи більше термінології.
дільник
Якщо d і a є натуральними числами, ми говоримо, що «d ділить a» якщо і тільки тоді, коли a ділиться на d, залишок дорівнює нулю. У цьому випадку ми говоримо, що «d - дільник a».
Наприклад, коли 36 ділиться на 4, залишок дорівнює нулю. У цьому випадку ми говоримо, що «4 - дільник 36». З іншого боку, коли 25 ділиться на 4, залишок не дорівнює нулю. У цьому випадку ми говоримо, що «4 - це не дільник 25».
Найбільший спільний дільник
Нехай a і b - натуральні числа. Спільними дільниками a і b є ті натуральні числа, які ділять як a, так і b. найбільший спільний дільник - найбільший з цих спільних дільників.
Приклад 1
Знайдіть найбільший спільний дільник 18 і 24.
Рішення
Спочатку перерахуйте дільники кожного числа, числа, які ділять кожне число з нульовим залишком.
Дільники 18:1, 2, 3, 6, 9 та 18
Дільники 24:1, 2, 3, 4, 6, 8, 12 і 24
Загальними дільниками є:
Загальні дільники: 1, 2, 3 та 6
Найбільший спільний дільник - найбільший із загальних дільників. Тобто,
Найбільший спільний дільник = 6.
Тобто найбільше число, яке ділить і 18, і 24 - це число 6.
Вправа
Знайдіть найбільший спільний дільник 12 і 18.
- Відповідь
-
6
Зменшення дробу до найнижчих
По-перше, визначення.
Найнижчі терміни
Дріб, як кажуть, зменшується до найнижчих, якщо найбільший спільний дільник чисельника і знаменника дорівнює 1.
Так, наприклад, 2/3 зводиться до найнижчих термінів, оскільки найбільший спільний подільник 2 і 3 дорівнює 1. З іншого боку, 4/6 не зводиться до найнижчих, оскільки найбільшим спільним дільником 4 та 6 є 2.
Приклад 2
Зменшити дріб 18/24 до найнижчих показників.
Рішення
Однією з прийомів, яка добре працює, є ділення як чисельника, так і знаменника на найбільший спільний дільник чисельника і знаменника. У прикладі 1 ми побачили, що найбільший спільний дільник 18 і 24 дорівнює 6. Ділимо і чисельник і знаменник на 6, щоб отримати
\[ \begin{aligned} \dfrac{18}{24} = \dfrac{18 \div 6}{24 \div 6} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 6.}} \\ = \dfrac{3}{4} ~ & \textcolor{red}{ \text{ Simplify numerator and dice.}} \end{aligned}\nonumber \]
Зверніть увагу, що найбільший спільний дільник 3 і 4 тепер 1. Таким чином, 3/4 зводиться до найнижчих термінів.
Є другий спосіб ми можемо показати поділ чисельника і знаменника на 6. По-перше, множник і чисельник, і знаменник наступним чином:
\[ \begin{aligned} \dfrac{18}{24} = \dfrac{3 \cdot 6}{4 \cdot 6} ~ & \textcolor{red}{ \text{ Factor out a 6.}} \end{aligned}\nonumber \]
Потім ви можете показати «ділення» як чисельника, так і знаменника на 6 шляхом «перекреслення» або «скасування» a 6 в чисельнику для 6 у знаменнику, ось так:
\[ \begin{aligned} = \dfrac{3 \cdot \cancel{6}}{4 \cdot \cancel{6}} ~ & \textcolor{red}{ \text{ Cancel common factor.}} \\ = \dfrac{3}{4} \end{aligned}\nonumber \]
Відзначимо, що ми отримуємо однаковий еквівалентний дріб, зменшений до найнижчих, а саме 3/4.
Вправа
Зменшити дріб 12/18 до найнижчих показників.
- Відповідь
-
2/3
Важливий момент
У прикладі 2 ми побачили, що 6 був як дільником, так і коефіцієнтом 18. Слова дільник і множник еквівалентні.
Ми використовували наступну техніку в нашому другому рішенні в прикладі 2.
Правило скасування
Якщо ви виражаєте чисельник і знаменник як добуток, то ви можете скасувати спільні множники з чисельника і знаменника. В результаті вийде еквівалентний дріб.
Через «Правило скасування» одним з найефективніших способів звести дріб до найнижчих чисел є спочатку пошук простих факторизацій як для чисельника, так і для знаменника, а потім скасування всіх загальних факторів.
Приклад 3
Зменшити дріб 18/24 до найнижчих показників.
Рішення
Використовуйте дерева множників для простого множника чисельника та знаменника.
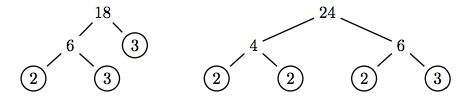
Після того, як ми врахували чисельник і знаменник, ми скасуємо загальні фактори.
\[ \begin{aligned} \dfrac{18}{24} = \dfrac{2 \cdot 3 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 3} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = \dfrac{ \cancel{2} \cdot \cancel{3} \cdot 3}{ \cancel{2} \cdot 2 \cdot 2 \cdot \cancel{3}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \dfrac{3}{2 \cdot 2} ~ & \textcolor{red}{ \text{ Remaining factors.}} \\ = \dfrac{3}{4} ~ & \textcolor{red}{ \text{ Simplify denominator.}} \end{aligned}\nonumber \]
Таким чином, 18/24 = 3/4.
Вправа\(\PageIndex{1}\)
Зменшити дріб 28/35 до найнижчих показників.
- Відповідь
-
4/5
Приклад 4
Зменшити дріб 28/42 до найнижчих показників.
Рішення
Використовуйте дерева множників для простого множника чисельника та знаменника.
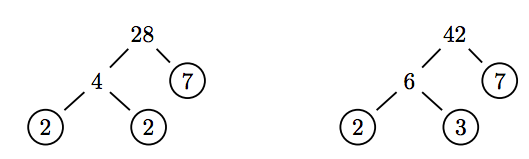
Тепер ми можемо скасувати загальні фактори.
\[ \begin{aligned} \dfrac{28}{42} = \dfrac{2 \cdot 2 \cdot 7}{2 \cdot 3 \cdot 7} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = \dfrac{ \cancel{2} \cdot 2 \cdot \cancel{7}}{ \cancel{2} \cdot 3 \cdot \cancel{7}} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \dfrac{2}{3} \end{aligned}\nonumber \]
Таким чином, 28/42 = 2/3.
Вправа
Зменшити дріб 36/60 до найнижчих показників.
- Відповідь
-
3/5
Зменшення дробів зі змінними
Точно таку ж методику ми використовуємо для зменшення дробів, чисельники та знаменники яких містять змінні.
Приклад 5
Зменшити
\[ \dfrac{56x^2y}{60xy^2}\nonumber \]
до найнижчих термінів.
Рішення
Використовуйте множникові дерева для множника коефіцієнтів чисельника та знаменника.

Тепер скасуйте загальні фактори.
\[ \begin{aligned} \dfrac{56x^2y}{60xy^2} = \dfrac{2 \cdot 2 \cdot 2 \cdot 7 \cdot x \cdot x \cdot y}{2 \cdot 2 \cdot 3 \cdot 5 \cdot x \cdot y \cdot y} ~ & \textcolor{red}{ \text{ Prime factor numerator and denominator.}} \\ = \dfrac{ \cancel{2} \cdot \cancel{2} \cdot 2 \cdot 7 \cdot \cancel{x} \cdot x \cdot \cancel{y}}{ \cancel{2} \cdot \cancel{2} \cdot 3 \cdot 5 \cdot \cancel{x} \cdot y \cdot \cancel{y}} ~ & \textcolor{red}{ \text{ Cancel cmmon factors.}} \\ = \dfrac{2 \cdot 7 \cdot x}{3 \cdot 5 \cdot y} ~ & \textcolor{red}{ \text{ Remaining factors.}} \\ = \dfrac{14x}{15y} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Таким чином, 56х 2 у/ (60х2) = 14х/ (15у).
Вправа
Зменшити:
\[ \dfrac{25a^3b}{40a^2b^3}\nonumber \]
- Відповідь
-
\[ \dfrac{5a}{8b^2}\nonumber \]
Слово про математичні позначення
Існує два типи математичних позначень: (1) вбудовані математичні позначення та (2) відображаються математичні позначення.
Вбудоване математичне позначення
Позначення 14 х/(15 у) називається вбудованим математичним позначенням. Коли той самий вираз центрується на власному рядку, як у
\[ \dfrac{14x}{15y},\nonumber \]
цей тип позначень називається відображеними математичними позначеннями.
Коли ви працюєте з задачею вручну, використовуючи розрахунки олівцем та папером, у бажаному форматі відображаються позначення, як і відображувані позначення, використані для спрощення даного виразу в прикладі 5. Однак комп'ютери та калькулятори вимагають введення виразів за допомогою вбудованих математичних позначень. Тому вкрай важливо, щоб ви були однаково компетентні або з математичними позначеннями: відображеними або вбудованими.
До речі, порядок операцій при застосуванні до вбудованого виразу 14x/ (15y) вимагає, щоб ми спочатку виконували множення всередині дужок. Тоді ми повинні виконувати множення та ділення, коли вони відбуваються, коли ми рухаємось зліва направо через вираз. Ось чому вбудоване позначення 14x/ (15y) еквівалентно відображеній нотації
\[ \dfrac{14x}{15y}.\nonumber \]
Однак вираз 14x/15y - це інший звір. Дужок немає, тому ми виконуємо множення і ділення в міру їх виникнення, рухаючись зліва направо через вираз. Таким чином, треба спочатку взяти добуток 14 і х, розділити результат на 15, потім помножити на y. в відображених позначеннях цей результат еквівалентний
\[ \dfrac{14x}{15} \cdot y,\nonumber \]
що є іншим результатом.
Деякі читачі можуть задатися питанням, чому ми не використали позначення (14x)/(15y) для опису рішення у прикладі 5. Адже це вбудоване позначення також еквівалентно відображуваної нотації.
\[ \dfrac{14x}{15y}.\nonumber \]
Однак справа в тому, що нам не потрібно, оскільки порядок операцій вже вимагає, щоб ми взяли добуток 14 і х перед діленням на 15y. Якщо це болить голова, знайте, що цілком допустимо використовувати еквівалентні позначення (14x)/(15y) замість 14x/ (15y). Обидва правильні.
Еквівалентні дроби у вищих термінами
Іноді виникає необхідність знайти еквівалентний дріб з іншим, більшим знаменником.
приклад 6
Висловіть 3/5 як еквівалентний дріб, що має знаменник 20.
Рішення
Ключ тут полягає в тому, щоб пам'ятати, що множення чисельника і знаменника на одне і те ж число дає еквівалентний дріб. Щоб отримати еквівалентний дріб зі знаменником 20, доведеться помножити чисельник і знаменник 3/5 на 4.
\[ \begin{aligned} \dfrac{3}{5} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 4.}} \\ = \dfrac{12}{20} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Тому 3/5 дорівнює 12/20.
Вправа
Висловіть 2/3 як еквівалентний дріб, що має знаменник 21.
- Відповідь
-
14/21
Приклад 7
Висловіть 8 як еквівалентний дріб, що має знаменник 5.
Рішення
Ключ тут полягає в тому, щоб відзначити, що
\[ \begin{aligned} 8 = \dfrac{8}{1} ~ & \textcolor{red}{ \text{ Understood denominator is 1.}} \end{aligned}\nonumber \]
Щоб отримати еквівалентний дріб зі знаменником 5, доведеться помножити чисельник і знаменник 8/1 на 5.
\[ \begin{aligned} = \dfrac{8 \cdot 5}{1 \cdot 5} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 5.}} \\ = \dfrac{40}{5} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Тому 8 дорівнює 40/5.
Вправа
Висловіть 5 як еквівалентний дріб, що має знаменник 7.
- Відповідь
-
35/7
Приклад 8
Експрес 2/9 як еквівалентний дріб, що має знаменник 18 а.
Рішення
Щоб отримати еквівалентний дріб зі знаменником 18 а, доведеться помножити чисельник і знаменник 2/9 на 2 a.
\[ \begin{aligned} \dfrac{2}{9} = \dfrac{2 \cdot 2a}{9 \cdot 2a} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by } 2a.} \\ = \dfrac{4a}{18a} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]
Отже, 2/9 дорівнює 4 a/(18 a), або еквівалентно, (4 а)/(18 a).
Вправа
Висловіть 3/8 як еквівалентний дріб, що має знаменник 24 а.
- Відповідь
-
\[ \dfrac{9a}{24a}\nonumber \]
Негативні дроби
Ми також маємо справу з фракціями, які є негативними. Для початку обговоримо розміщення негативного знака.
- Позитивний розділений на негативний є негативним, тому
\[ \dfrac{3}{-5} = - \dfrac{3}{5}.\nonumber \]
- Але вірно і те, що негатив, розділений на позитивний, є негативним. Таким чином,
\[ \dfrac{−3}{5} = \dfrac{−3}{5}.\nonumber \]
Ці два спостереження мають на увазі, що всі три з наступних дробів еквівалентні (однакове число):
\[ \dfrac{3}{-5} = - \dfrac{3}{5} = \dfrac{-3}{5}.\nonumber \]
Зауважте, що існує три можливі місця розташування негативного знака: (1) знаменник, (2) рядок дробу або (3) чисельник. Будь-яке з цих місць розташування дає еквівалентний дріб.
Дроби і негативні знаки
Нехай a і b будуть будь-якими цілими числами. Всі три з наступних дробів еквівалентні (однакове число):
\[ \dfrac{a}{-b} = - \dfrac{a}{b} = \dfrac{-a}{b}.\nonumber \]
Математики вважають за краще розміщувати негативний знак або в чисельнику, або на бруску дробу. Використання негативного знака в знаменнику не рекомендується.
Приклад 9
Зменшити:
\[ \dfrac{50x^3}{-75x^5}\nonumber \]
до найнижчих термінів.
Рішення
Простий множник чисельник і знаменник і скасування.
\[ \begin{aligned} \dfrac{50x^3}{-75x^5} &= \dfrac{2 \cdot 5 \cdot 5 \cdot x \cdot x \cdot x}{-3 \cdot 5 \cdot 5 \cdot x \cdot x \cdot x \cdot x \cdot x} \\ &= \dfrac{2 \cdot \cancel{5} \cdot \cancel{5} \cdot \cancel{x} \cdot \cancel{x} \cdot \cancel{x}}{-3 \cdot \cancel{5} \cdot \cancel{5} \cdot \cancel{x} \cdot \cancel{x} \cdot \cancel{x} \cdot x \cdot x} \\ &= \dfrac{2}{-3 \cdot x \cdot x} \\ &= \dfrac{2}{-3x^2} \end{aligned}\nonumber \]
Однак бажано, щоб в знаменнику не було негативних знаків, тому поставимо негативний знак на брусок дробу (чисельник підійде також). Таким чином,
\[ \dfrac{50x^3}{-75x^5} = - \dfrac{2}{3x^2}\nonumber \]
У нас також є наступний результат.
Дроби і негативні знаки
\(b\)Дозволяти\(a\) і бути будь-якими цілими числами. Потім,
\[ \dfrac{-a}{-b} = \dfrac{a}{b}.\nonumber \]
приклад 10
Зменшити:
\[ \dfrac{-12xy^2}{-18x^2y}\nonumber \]
Рішення
На відміну від Прикладу 9, деякі люблять спочатку подбати про знак відповіді.
\[ \dfrac{-12xy^2}{-18x^2y} = \dfrac{12xy^2}{18x^2y}\nonumber \]
Тепер ми можемо перерахувати чисельник і знаменник і скасувати загальні множники.
\[ \begin{aligned} &= \dfrac{2 \cdot 2 \cdot 3 \cdot x \cdot y \cdot y}{2 \cdot 3 \cdot 3 \cdot x \cdot x \cdot y} \\ &= \dfrac{ \cancel{2} \cdot 2 \cancel{3} \cdot \cancel{x} \cdot y \cdot \cancel{y}}{ \cancel{2} \cdot \cancel{3} \cdot 3 \cdot \cancel{x} \cdot x \cdot \cancel{y}} &= \dfrac{2y}{3x} \end{aligned}\nonumber \]
Таким чином,
\[ \dfrac{-12xy^2}{-18x^2y} = \dfrac{2y}{3x}.\nonumber \]
Вправа
Зменшити:
\[ \dfrac{-21a^2b^3}{-56a^3b}\nonumber \]
- Відповідь
-
\[ \dfrac{3b^2}{8a}\nonumber \]
Вправи
У вправах 1-12 знайдіть НСД заданих чисел.
1. 72, 8
2. 76, 52
3. 52, 20
4. 56, 96
5. 36, 63
6. 63, 21
7. 72, 44
8. 10, 40
9. 16, 56
10. 54, 66
11. 84, 24
12. 75, 45
У вправах 13-28 зменшіть задану дріб до найнижчих.
13. \(\dfrac{22}{98}\)
14. \(\dfrac{28}{56}\)
15. \(\dfrac{93}{15}\)
16. \(\dfrac{90}{39}\)
17. \(\dfrac{69}{21}\)
18. \(\dfrac{74}{62}\)
19. \(\dfrac{74}{12}\)
20. \(\dfrac{66}{10}\)
21. \(\dfrac{66}{57}\)
22. \(\dfrac{34}{30}\)
23. \(\dfrac{33}{99}\)
24. \(\dfrac{20}{58}\)
25. \(\dfrac{69}{24}\)
26. \(\dfrac{18}{96}\)
27. \(\dfrac{46}{44}\)
28. \(\dfrac{92}{24}\)
29. Експрес 3 як еквівалентний дріб, що має знаменник 24. 30. Висловити 3 як еквівалентний дріб, що має знаменник 8. 31. \(\dfrac{25}{19}\)Висловити як еквівалентний дріб, що має знаменник 57. 32. \(\dfrac{29}{22}\)Висловити як еквівалентний дріб, що має знаменник 44. 33. Експрес 2 як еквівалентний дріб, що має знаменник 2. 34. Висловіть 2 як еквівалентний дріб, що має знаменник 8. 35. \(\dfrac{18}{19}\)Висловити як еквівалентний дріб, що має знаменник 95. 36. \(\dfrac{17}{22}\)Висловити як еквівалентний дріб, що має знаменник 44. 37. \(\dfrac{1}{3}\)Висловити як еквівалентний дріб, що має знаменник 24. 38. \(\dfrac{15}{19}\)Висловити як еквівалентний дріб, що має знаменник 95. 39. Висловіть 16 як еквівалентний дріб, що має знаменник 4. 40. Експрес 5 як еквівалентний дріб, що має знаменник 2.
У вправах 41-56 зменшіть задану дріб до найнижчих.
41. \(\dfrac{34}{−86}\)
42. \(\dfrac{−48}{14}\)
43. \(\dfrac{−72}{−92}\)
44. \(\dfrac{27}{−75}\)
45. \(\dfrac{−92}{82}\)
46. \(\dfrac{−44}{−62}\)
47. \(\dfrac{−21}{33}\)
48. \(\dfrac{57}{−99}\)
49. \(\dfrac{22}{−98}\)
50. \(\dfrac{−33}{69}\)
51. \(\dfrac{42}{−88}\)
52. \(\dfrac{−100}{48}\)
53. \(\dfrac{94}{−6}\)
54. \(\dfrac{−36}{−38}\)
55. \(\dfrac{10}{−86}\)
56. \(\dfrac{−100}{−46}\)
57. Експрес\(\dfrac{3}{2}\) як еквівалентний дріб, що має знаменник 62n.
58. Експрес\(\dfrac{6}{25}\) як еквівалентний дріб, що має знаменник 50а.
59. Експрес\(\dfrac{13}{10}\) як еквівалентний дріб, що має знаменник 60m.
60. Експрес\(\dfrac{1}{16}\) як еквівалентний дріб, що має знаменник 80p.
61. Експрес\(\dfrac{3}{2}\) як еквівалентний дріб, що має знаменник 50n.
62. Експрес\(\dfrac{43}{38}\) як еквівалентний дріб, що має знаменник 76а.
63. Експрес 11 як еквівалентний дріб, що має знаменник 4м. 64. Висловіть 13 як еквівалентний дріб, що має знаменник 6n.
65. Експрес 3 як еквівалентний дріб, що має знаменник 10м.
66. Висловіть 10 як еквівалентний дріб, що має знаменник 8b.
67. Висловіть 6 як еквівалентний дріб, що має знаменник 5n.
68. Експрес 16 як еквівалентний дріб, що має знаменник 2у.
У вправах 69-84 зменшіть задану дріб до найнижчих.
69. \(\dfrac{82y^5}{−48y}\)
70. \(\dfrac{−40y^5}{−55y}\)
71. \(\dfrac{−77x^5}{44x^4}\)
72. \(\dfrac{−34x^6}{−80x}\)
73. \(\dfrac{−14y^5}{54y^2}\)
74. \(\dfrac{96y^4}{−40y^2}\)
75. \(\dfrac{42x}{81x^3}\)
76. \(\dfrac{26x^2}{32x^6}\)
77. \(\dfrac{−12x^5}{14x^6}\)
78. \(\dfrac{−28y^4}{72y^6}\)
79. \(\dfrac{−74x}{22x^2}\)
80. \(\dfrac{56x^2}{26x^3}\)
81. \(\dfrac{−12y^5}{98y^6}\)
82. \(\dfrac{96x^2}{14x^4}\)
83. \(\dfrac{18x^6}{−54x^2}\)
84. \(\dfrac{32x^6}{62x^2}\)
У вправах 85-100 зменшіть задану дріб до найнижчих.
85. \(\dfrac{26y^2x^4}{−62y^6x^2}\)
86. \(\dfrac{6x^2y^3}{40x^3y^2}\)
87. \(\dfrac{−2y^6x^4}{−94y^2x^5}\)
88. \(\dfrac{90y^6x^3}{39y^3x^5}\)
89. \(\dfrac{30y^5x^5}{−26yx^4}\)
90. \( \dfrac{74x^6y^4}{−52xy^3}\)
91. \(\dfrac{36x^3y^2}{−98x^4y^5}\)
92. \(\dfrac{84x^3y}{16x^4y^2}\)
93. \(\dfrac{−8x^6y^3}{54x^3y^5}\)
94. \( \dfrac{70y^5x^2}{16y^4x^5}\)
95. \(\dfrac{34yx^6}{−58y^5x^4}\)
96. \(\dfrac{99y^2x^3}{88y^6x}\)
97. \(\dfrac{−36y^3x^5}{51y^2x}\)
98. \(\dfrac{44y^5x^5}{−88y^4x}\)
99. \(\dfrac{91y^3x^2}{−28y^5x^5}\)
100. \(\dfrac{−76y^2x}{−57y^5x^6}\)
101. Урагани. За даними Національного управління атмосфери та океаніки, у 2008 році було 16 названих штормів, з яких 8 переросли в урагани, а 5 - великі.
i) Яка частка названих штормів переросла в урагани? Зменшіть свою відповідь до найнижчих термінів.
ii) Яка частка названих штормів були великими ураганами? Зменшіть свою відповідь до найнижчих термінів.
iii) Яка частка ураганів була основною? Зменшіть свою відповідь до найнижчих термінів.
102. Тигри. Тигри перебувають у критичному занепаді через посягання людини, втрати більше дев'яти десятих місць свого проживання та зростаючої торгівлі тигровими шкурами та частинами тіла. Associated Прес-Час-Стандарт 01/24/10 Кріплення під тиском, щоб врятувати тигра.
i) Запишіть втрату середовища проживання у вигляді дробу.
ii) Опишіть словами, що представляють собою чисельник і знаменник цього дробу.
iii) Якщо фракція являє собою втрату всього вихідного середовища існування, скільки залишилося вихідного середовища існування?
Відповіді
1. 8
3. 4
5. 9
7. 4
9. 8
11. 12
13. \(\dfrac{11}{49}\)
15. \(\dfrac{31}{5}\)
17. \(\dfrac{23}{7}\)
19. \(\dfrac{37}{6}\)
21. \(\dfrac{22}{19}\)
23. \(\dfrac{1}{3}\)
25. \(\dfrac{23}{8}\)
27. \(\dfrac{23}{22}\)
29. \(\dfrac{72}{24}\)
31. \(\dfrac{75}{57}\)
33. \(\dfrac{4}{2}\)
35. \(\dfrac{90}{95}\)
37. \(\dfrac{8}{24}\)
39. \(\dfrac{64}{4}\)
41. \(\dfrac{−17}{43}\)
43. \(\dfrac{18}{23}\)
45. \(\dfrac{−46}{41}\)
47. \(\dfrac{− 7}{11}\)
49. \(\dfrac{−11}{49}\)
51. \(\dfrac{−21}{44}\)
53. \(\dfrac{−47}{3}\)
55. \(\dfrac{− 5}{43}\)
57. \(\dfrac{93 n}{62 n}\)
59. \(\dfrac{78 m}{60 m}\)
61. \(\dfrac{75 n}{50 n}\)
63. \(\dfrac{44 m}{4 m}\)
65. \(\dfrac{30 m}{10 m}\)
67. \(\dfrac{30 n}{5 n}\)
69. \(\dfrac{−41 y^4}{24}\)
71. \(\dfrac{− 7x}{4}\)
73. \(− \dfrac{7 y^3}{27}\)
75. \(\dfrac{14}{27 x^2}\)
77. \(− \dfrac{6}{7x}\)
79. \(− \dfrac{37}{11 x}\)
81. \(− \dfrac{6}{49 y}\)
83. \(− \dfrac{x^4}{3}\)
85. \(− \dfrac{13 x^2}{31 y^4}\)
87. \(\dfrac{y^4}{47 x}\)
89. \(− \dfrac{15 y^4 x}{13}\)
91. \(− \dfrac{18}{49xy^3}\)
93. \(− \dfrac{4 x^3}{27 y^2}\)
95. \(−\dfrac{17 x^2}{29 y^4}\)
97. \(− \dfrac{12yx^4}{17}\)
99. \(− \dfrac{13}{4y^2x^3}\)
101.
i)\(\dfrac{1}{2}\)
ii)\(\dfrac{5}{16}\)
iii)\(\dfrac{5}{8}\)
