3.4: Поєднання подібних термінів

Починаємо нашу дискусію з визначення терміна.

Визначення: Термін

Термін - це одне число або змінна, або він може бути добутком числа (називається його коефіцієнтом) і однієї або декількох змінних (званих його змінною частиною). Терміни в алгебраїчному виразі відокремлюються символами додавання.

Приклад 1

Визначте терміни в алгебраїчному виразі

$$3x^2 + 5xy + 9y^2 + 12\nonumber$$

Для кожного члена визначте його коефіцієнт і змінну частину.

Рішення

У табличній формі перерахуємо кожен член виразу 3x^2 + 5xy + 9y^2 + 12, його коефіцієнт та його змінну частину.

Термін	Коефіцієнт	Змінна частина
3 х ^2	3	х ^2
5 xy	5	xy
9 з ^2	9	на ^2
12	12	Жоден

Вправа

Скільки членів в алгебраїчному виразі 3 x ^{2 + 2} xy − 3 y ²?

Відповідь

3

Приклад 2

Визначте терміни в алгебраїчному виразі

$$a^3 − 3a^2b + 3ab^2 − b^3\nonumber$$

Для кожного члена визначте його коефіцієнт і змінну частину.

Рішення

Першим кроком є написання кожної різниці у вигляді суми, оскільки терміни виразу визначені вище як елементи, розділені символами додавання.

$$a^3 + (−3a^2b)+3ab^2 + (−b^3)\nonumber$$

У табличній формі перерахуємо кожен член виразу$a^3+(−3a^2b)+3ab^2+(−b^3)$, його коефіцієнт і його змінну частину.

Термін	Коефіцієнт	Змінна частина
a ^3	1	a ^3
-3 а ^2 б	−3	а ^2 б
3 аб ^2	3	аб ^2
− b ^3	−1	б ^3

Вправа

Скільки термінів в алгебраїчному виразі$11 − a^2 − 2ab + 3b^2a$?

Відповідь

4

Подобається Умови

Ми визначаємо, що мається на увазі під «подібними термінами» і «на відміну від термінів».

Визначення

Як і на відміну від термінів. Змінні частини двох термінів визначають, чи є терміни подібними до термінів чи на відміну від термінів.

Подібні терміни. Два члени називаються як терміни, якщо вони мають однакові змінні частини, а це означає, що терміни повинні містити однакові змінні, підняті до однакових експоненціальних степеней.

На відміну від Умов. Два члени називаються на відміну від термінів, якщо їх змінні частини різні.

Приклад 3

Класифікувати кожну з наступних пар як подібні терміни або відмінні від термінів: (a) 3 x та −7 x, (b) 2 y та 3 y ², (c) −3 t та 5 u та (d) −4 a ³ і 3 а ³.

Рішення

Подібні терміни повинні мати однакові змінні частини.

1. 3 x та −7 x мають однакові змінні частини. Вони «як терміни».
2. 2 у і 3 у ² не мають однакових змінних частин (показники відрізняються). Вони «на відміну від термінів».
3. −3 t та 5 u не мають однакових змінних частин (різних змінних). Вони «на відміну від термінів».
4. −4 a ³ та 3 a ³ мають однакові змінні частини. Вони «як терміни».

Вправа

Чи є −3 xy та 11 xy подібними або несхожими на терміни?

Відповідь

Подібні терміни

Поєднання подібних термінів

При використанні розподільної властивості не має різниці, чи є множення ліворуч чи праворуч, все одно розподіляє множення разів на кожен член в дужках.

Розподільна власність

Якщо a, b і c є цілими числами, то

а (б + с) = аб + ак і (б + с) а = ба + ка.

У будь-якому випадку ви розподіляєте раз кожен член суми.

«Подібні терміни» можна комбінувати і спрощувати. Інструмент, який використовується для об'єднання подібних термінів, є розподільна властивість. Наприклад, розглянемо вираз 3 y + 7 y, що складається з двох «подібних термінів» із загальною змінною частиною. Ми можемо використовувати розподільну властивість і писати

$$3y+7y=(3+7)y\nonumber$$

Зверніть увагу, що ми використовуємо розподільну властивість у зворотному напрямку, «факторинг» загальної змінної частини кожного члена. Перевіряючи нашу роботу, зверніть увагу, що якщо ми перерозподіляємо змінну part y раз на кожен член в дужках, ми повернемося до вихідного виразу 3 y + 7 y.

Приклад 4

Використовуйте розподільну властивість для об'єднання подібних термінів (якщо можливо) у кожному з наступних виразів: (a) −5 x ² − 9 x ², (b) −5 ab + 7 ab, (c) 4 y ³ − 7 y ² та (d) 3 xy ² − 7 хх ².

Рішення

Якщо терміни «схожі на терміни», ви можете використовувати розподільну властивість, щоб «зарахувати» загальну змінну частину.

а) Фактор із загальної змінної частини x ².

$$\begin{aligned} -5x^2 -9x^2 =(-5-9)x^2 ~ & \textcolor{red}{ \text{ Use the distributive property.}} \\ = -14x^2 ~ & \textcolor{red}{ \text{ Simplify: } -5-9=-5+(-9) = -14.} \end{aligned}\nonumber$$

б) Фактор із загальної змінної частини ab.

$$\begin{aligned} -5ab +7ab = (-5+7)ab ~ & \textcolor{red}{ \text{ Use the distributive property.}} \\ =2ab ~ & \textcolor{red}{ \text{ Simplify: } -5+7 = 2.} \end{aligned}\nonumber$$

c) Терміни у виразі 4 y ³ − 7 y ² мають різні змінні частини (експоненти різні). Це «на відміну від термінів» і не можуть бути об'єднані.

г) Фактор із загальної змінної частини xy ².

$$\begin{aligned} 3xy^2 - 7xy^2 =(3-7)xy^2 ~ & \textcolor{red}{ \text{ Use the distributive property.}} \\ =-4xy^2 ~ & \textcolor{red}{ \text{ Simplify: } 3-7=3+(-7)=-4.} \end{aligned}\nonumber$$

Вправа

Спрощення: −8 z − 11 z

Відповідь

−19 з

Прискорення речей трохи

Після того, як ви виписали всі кроки для об'єднання подібних термінів, як ті, що показані в прикладі 4, ви можете трохи прискорити процес, дотримуючись цього правила:

Поєднання подібних термінів

Щоб об'єднати подібні терміни, просто додайте їх коефіцієнти і збережіть загальну змінну частину.

Так, наприклад, коли представлена сума двох подібних членів, таких як у 5 х + 8 х, просто додайте коефіцієнти і повторіть загальну змінну частину; тобто 5 х + 8 х = 13 х.

Приклад 5

Поєднуйте подібні терміни:

1. −9 г − 8г,
2. −3 y ⁵ + 4 y ⁵ та
3. −3 у ² + 2 у ².

Рішення

а) Скласти коефіцієнти і повторити загальну змінну частину. Тому,

$$−9y − 8y = −17y.\nonumber$$

б) Скласти коефіцієнти і повторити загальну змінну частину. Тому,

$$−3y^5 + 4y^5 = 1y^5.\nonumber$$

Однак врахуйте, що 1 у ⁵ = у ⁵. Дотримуючись правила, що остаточна відповідь повинна використовувати якомога менше символів, кращою відповіддю буде −3 y ⁵ + 4 y ⁵ = y ⁵.

в) Скласти коефіцієнти і повторити загальну змінну частину. Тому,

$$−3u^2 + 2u^2 = (−1)u^2.\nonumber$$

Однак зауважте, що (−1) u ² = − u ². Дотримуючись правила, що остаточна відповідь має використовувати якомога менше символів, кращою відповіддю буде −3 u ² + 2 u ² = − u ².

Вправа

Об'єднати: −3 x, і − 4 x ²

Відповідь

−7 х ²

Спростити

Часто зустрічається інструкція просить читача спростити вираз.

Спростити

Інструкція спростити - це загальний термін, який означає «спробуйте написати вираз в його найбільш компактному вигляді, використовуючи найменшу кількість символів».

Одним із способів досягнення цієї мети є поєднання подібних термінів, коли вони присутні.

Приклад 6

Спрощення: 2 x + 3 y − 5 x + 8 y.

Рішення

Використовуйте комутативну властивість для зміни порядку термінів та асоціативних та розподільних властивостей для перегрупування та об'єднання подібних термінів.

$$\begin{aligned} 2x + 3y - 5x + 8y = (2x - 5x) + (3y + 8y) ~ & \textcolor{red}{ \text{ Reorder and regroup.}} \\ = -3x + 11y ~ & \textcolor{red}{ \text{ Combine like terms:}} \\ ~ & \textcolor{red}{ 2x - 5x = -3x \text{ and } 3y + 8y = 11y.} \end{aligned}\nonumber$$

альтернативне рішення

Звичайно, вам не потрібно показувати крок перегрупування. Якщо вам зручніше поєднувати подібні терміни в голові, ви можете представити свою роботу наступним чином:

$$2x + 3y − 5x + 8y = −3x + 11y.\nonumber$$

Вправа

Спрощення: −3 a + 4 b − 7 a − 9 b

Відповідь

−10 a − 5 б

Приклад 7

Спрощення: −2 x − 3 − (3 x + 4).

Рішення

Спочатку розподіліть негативний знак.

$$\begin{aligned} -2x-3-(3x+4)= -2x-3-3x-4 ~ & \textcolor{red}{-(3x+4)=-3x-4.} \end{aligned}\nonumber$$

Далі використовуйте комутативну властивість для переупорядкування, потім асоціативну властивість перегрупувати. Потім комбінуйте подібні терміни.

$$\begin{aligned} =(-2x-3x)+(-3-4) ~ & \textcolor{red}{ \text{ Reorder and regroup.}} \\ =-5x+(-7) ~ & \textcolor{red}{ \text{ Combine like terms:}} \\ ~ & \textcolor{red}{ -2x-3x=-5x.} \\ =-5x-7 ~ & \textcolor{red}{ \text{ Simplify:}} \\ ~ & \textcolor{red}{-5x+(-7)=-5x-7.} \end{aligned}\nonumber$$

альтернативне рішення

Ви можете пропустити другий крок, якщо хочете, просто поєднуючи подібні терміни подумки. Тобто цілком можливо замовити свою роботу наступним чином:

$$\begin{aligned} -2x-3-(3x+4) = -2x-3-3x-4 ~ & \textcolor{red}{ \text{ Distribute negative sign.}} \\ =-5x-7 ~ & \textcolor{red}{ \text{ Combine like terms.}} \end{aligned}\nonumber$$

Вправа

Спрощення: −9 a − 4 − (4 a − 8)

Відповідь

−13 а + 4

Приклад 8

Спрощення: 2 (5 − 3 x) − 4 (x + 3).

Рішення

Використовуйте розподільну властивість для розширення, а потім використовуйте комутативні та асоціативні властивості, щоб згрупувати подібні терміни та об'єднати їх.

$$\begin{aligned} 2(5-3x)-4(x+3) = 10-6x-4x-12 ~ & \textcolor{red}{ \text{ Use the distributive property.}} \\ =(-6x-4x)+(10-12) ~ & \textcolor{red}{ \text{ Group like terms.}} \\ =-10x-2 ~ & \textcolor{red}{ \text{ Combine like terms: }} \\ ~ & \textcolor{red}{-6x-4x=-10x \text{ and} \\ ~ & \textcolor{red}{10-12=-2.} \end{aligned}\nonumber$$

альтернативне рішення

Ви можете пропустити другий крок, якщо хочете, просто поєднуючи подібні терміни подумки. Тобто цілком можливо замовити свою роботу наступним чином:

$$\begin{aligned} 2(5-3x)-4(x+3) = 10-6x-4x-12 ~ & \textcolor{red}{ \text{ Distribute.}} \\ =-10x-2 ~& \textcolor{red}{ \text{ Combine like terms.}} \end{aligned}\nonumber$$

Вправа

Спрощення: −2 (3 a − 4) − 2 (5 − a)

Відповідь

−4 a − 2

Приклад 9

Спрощення: −8 (3 x ² y − 9 xy) − 8 (−7 x ² − 8 xy)

Рішення

Ми будемо діяти трохи швидше з цим рішенням, використовуючи розподільну властивість розширювати, потім поєднуючи подібні терміни подумки.

$$\begin{aligned} -8(3x^2y-9xy) -8(-7x^2y-8xy)=-24x^2y+72xy+56x^2y+64xy \\ = 32x^2y+136xy \end{aligned}\nonumber$$

Вправа

Спрощення: (a ² − 2 аб) − 2 (3 аб + a ²)

Відповідь

− ² − 8 аб

Додатки

Ми можемо спростити ряд корисних формул, поєднуючи подібні терміни.

Приклад 10

Знайдіть периметр P прямокутника (a) та (b) квадрата, зображеного нижче. Максимально спрощуйте свою відповідь.

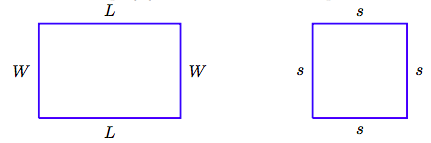
Рішення

Периметр будь-якої багатокутної фігури - це сума довжин її сторін.

а) Щоб знайти периметр P прямокутника, підсумуйте його чотири сторони.

$$P = L + W + L + W.\nonumber$$

Поєднуйте подібні терміни.

$$P = 2L + 2W.\nonumber$$

б) Щоб знайти периметр P квадрата, підсумуйте його чотири сторони.

$$P = s + s + s + s.\nonumber$$

Поєднуйте подібні терміни.

$$P = 4s.\nonumber$$

Вправа

Правильний шестикутник має шість рівних сторін, кожна з яких має довжину х. Знайти його периметр через x.

Відповідь

Р = 6 х

Іноді корисно замінити змінну виразом, що містить іншу змінну.

Приклад 11

Довжина прямокутника на три фути більше, ніж в два рази більше його ширини. Знайдіть периметр P прямокутника лише через його ширину.

Рішення

З попередньої задачі периметр прямокутника задається

$$P = 2L + 2W,\nonumber$$

де L і W - довжина і ширина прямокутника відповідно. Це рівняння дає периметр з точки зору його довжини та ширини, але ми попросили отримати периметр лише через ширину. Однак ми також враховуємо той факт, що довжина на три фути довша, ніж удвічі більше ширини.

$$\begin{array} \colorbox{cyan}{Length} & \text{ is } & \colorbox{cyan}{Three Feet} & \text{ longer than } & \colorbox{cyan}{Twice the Width} \\ L & = & 3 & + & 2W \end{array}\nonumber$$

Оскільки L = 3+2 W, ми можемо замінити L на 3+2 W в рівнянні периметра 3.1.

$$P = 2L + 2W\nonumber$$

$$P = 2(3 + 2W)+2W\nonumber$$

Використовуйте розподільну властивість, а потім комбінуйте подібні терміни.

$$P =6+4W + 2W\nonumber$$

$$P =6+6W.\nonumber$$

Це останнє рівняння дає периметр P через ширину тільки W.

Вправа

Довжина L прямокутника на 5 метрів більше, ніж в два рази більше його ширини W. Знайти периметр P прямокутника через його ширину W.

Відповідь

Відповідь: Р = 6 Вт+ 10

Приклад 12

Ширина прямокутника на два фути менше його довжини. Знайдіть периметр P прямокутника лише через його довжину.

Рішення

Знову ж, периметр прямокутника задається рівнянням

$$P = 2L + 2W,\nonumber$$

де L і W - довжина і ширина прямокутника відповідно. Це рівняння дає периметр з точки зору його довжини та ширини, але ми попросили отримати периметр лише через довжину.

Однак ми також враховуємо той факт, що ширина на два фути менше довжини.

$$\begin{aligned} \colorbox{cyan}{Width} & \text{ is } & \colorbox{cyan}{Length} & \text{ minus } & \colorbox{cyan}{Two feet} \\ W & = & L & - & 2 \end{aligned}\nonumber$$

Оскільки W = L −2, ми можемо замінити W на L −2 у рівнянні периметра 3.2.

$$P = 2L + 2W\nonumber$$

$$P = 2L + 2(L − 2)\nonumber$$

Використовуйте розподільну властивість, а потім комбінуйте подібні терміни.

$$P = 2L + 2L − 4\nonumber$$

$$P = 4L − 4.\nonumber$$

Це останнє рівняння дає периметр P через довжину L поодинці.

Вправа

Ширина W прямокутника на 5 футів менше, ніж удвічі більше ширини L. Знайти периметр P прямокутника через його довжину L.

Відповідь

Р = 6 Л − 10

Вправи

У вправах 1-16 об'єднайте подібні терміни, спочатку використовуючи розподільну властивість, щоб вивести загальну змінну частину, а потім спрощуючи.

1. 17хх ² + 18х ² + 20хх ²

2. 13хх − 3хх+ х

3. −8xy ² − 3xy ² − 10xy ²

4. −12xy − 2хх+10хх

5. 4хх − 20хх

6. −7й ³ + 15й ³

7. 12р − 12р

8. 16 років − 5

9. −11х − 13х+ 8х

10. −9р − 10р + 3р

11. −5кв + 7кв

12. 17н +15н

13. р − 13р − 7р

14. 19м + м +15м

15. 3х ³ − 18х ³

16. 13х ² у + 2х ² г

---

У Вправи 17-32 об'єднайте подібні терміни, спочатку переставляючи терміни, потім використовуючи розподільну властивість, щоб виділити загальну змінну частину, а потім спрощуючи.

17. −8 +17н +10 + 8н

18. 11 + 16 с − 14 − 6

19. −2х ³ − 19х ² у − 15х ² у + 11х ³

20. −9х ² у − 10й ³ − 10й ³ + 17х ² у

21. −14xy − 2х ³ − 2х ³ − 4х

22. −4х ³ + 12х+4хх − 12х ³

23. −13 +16м + м + 16

24. 9 − 11х − 8х + 15

25. −14х ² у − 2хх ² + 8х ² у + 18х ²

26. −19й ² + 18й ³ − 5й ² − 17 років ³

27. −14х ³ + 16х+5х ³ + 8х

28. −16xy + 16 років ² + 7хх + 17 років ²

29. 9н + 10 + 7 +15н

30. −12р + 5 +17 +17р

31. 3й +1+6й + 3

32. 19р +6+8р + 13

---

У вправах 33-56 спростіть вираз, спочатку використовуючи розподільну властивість для розширення виразу, а потім переставляючи і поєднуючи подібні терміни подумки.

33. −4 (9х ² у + 8) + 6 (10х ² у − 6)

34. −4 (−4xy + 5y ³) + 6 (−5xy − 9y ³)

35. 3 (−4х ² + 10г ²) + 10 (4й ² − х ²)

36. −7 (−7х ³ + 6х ²) − 7 (−10х ² − 7х ³)

37. −s + 7 − (−1 − 3с)

38. 10 років − 6 − (−10 − 10 років)

39. −10q − 10 − (−3q + 5)

40. −2n + 10 − (7n − 1)

41. 7 (8 років + 7) − 6 (8 − 7 років)

42. −6 (−5n − 4) − 9 (3+ 4n)

43. 7 (10х ² − ^8х2) − 7 (9хх ² + 9х ²)

44. 10 (8х ² у − 10хх ²) + 3 (8хх ² + 2х ² у)

45. −2 (6 + 4n) + 4 (−n − 7)

46. −6 (−2 − 6м) + 5 (−9м+ 7)

47. 8 − (4 + 8 років)

48. −1 − (8 + с)

49. −8 (−n + 4) − 10 (−4n + 3)

50. 3 (8р − 7) − 3 (2р − 2)

51. −5 − (10п + 5)

52. −1 − (2p − 8)

53. 7 (1 + 7р) + 2 (4 − 5р)

54. (5 − с) + 10 (9 + 5 с)

55. −2 (−5 − 8x ²) − 6 (6)

56. 8 (10 років ² + 3х ³) − 5 (−7й ² − 7х ³)

---

57. Довжина L прямокутника на 2 фути більше, ніж у 6 разів його ширина W. Знайти периметр прямокутника лише через його ширину.

58. Довжина L прямокутника в 7 футів більше, ніж 6 разів його ширина W. Знайти периметр прямокутника лише через його ширину.

59. Ширина W прямокутника на 8 футів коротша за його довжину L. Знайдіть периметр прямокутника лише через його довжину.

60. Ширина W прямокутника на 9 футів коротша за його довжину L. Знайдіть периметр прямокутника лише через його довжину.

61. Довжина L прямокутника на 9 футів коротше, ніж у 4 рази його ширина W. Знайти периметр прямокутника лише через його ширину.

62. Довжина L прямокутника на 2 фути коротше, ніж у 6 разів його ширина W. Знайти периметр прямокутника лише через його ширину.

---

Відповіді

1. 55xy ²

3. −21xy ²

5. −16xy

7. 0

9. −16х

11. 2кв

13. −19р

15. −15х ³

17. 2 +25н

19. 9х ³ − 34х ² р

21. −18xy − 4х ³

23. 3 + 17м

25. -6х ² у + 16xy ²

27. -9х ³ + 24 роки

29. Цілодобовий + 17

31. 9 років + 4

33. 24 х ² р − 68

35. −22х ² + 70 р ²

37. 2 с + 8

39. −7q − 15

41. 98-й + 1

43. 7х ² − 119хх ²

45. −40 − 12н

47. 4 − 8 років

49. 48n − 62

51. −10 − 10 п

53. 15 +39р

55. -26 + 16х ²

57. 4 +14 ВТ

59. 4 Л − 16

61. 10 ВТ − 18