9.1: Послідовності
- Page ID
- 62241
- Знайдіть формулу для загального члена послідовності.
- Обчисліть межу послідовності, якщо вона існує.
- Визначте збіжність або розбіжність заданої послідовності.
У цьому розділі ми вводимо послідовності та визначаємо, що означає, що послідовність сходиться або розходиться. Ми показуємо, як знайти межі послідовностей, які сходяться, часто за допомогою властивостей меж для функцій, розглянутих раніше. Ми закриваємо цей розділ теоремою монотонної збіжності, інструментом, який ми можемо використовувати, щоб довести, що певні типи послідовностей сходяться.
Термінологія послідовностей
Для роботи з цією новою темою нам потрібні нові терміни та визначення. По-перше, нескінченна послідовність - це впорядкований список номерів виду
\[a_1,a_2,a_3,…,a_n,….\nonumber \]
Кожне з чисел в послідовності називається терміном. Символ\(n\) називається змінною index для послідовності. Використовуємо позначення
\[\{a_n\}^∞_{n=1},\nonumber \]
або просто\(\{a_n\}\), позначити цю послідовність. Подібне позначення використовується для множин, але послідовність - це впорядкований список, тоді як множина не впорядкована. Оскільки конкретне число\(a_n\) існує для кожного додатного цілого числа\(n\), ми також можемо визначити послідовність як функцію, область якої є набором натуральних чисел.
Розглянемо нескінченний, упорядкований список
\[2,4,8,16,32,….\nonumber \]
Це послідовність, в якій перший, другий і третій терміни задаються\(a_1=2, a_2=4,\) і\(a_3=8.\) Ви, ймовірно, бачите, що терміни в цій послідовності мають наступну закономірність:
\[a_1=2^1,\,a_2=2^2,\,a_3=2^3,\,a_4=2^4 \text{ and } a_5=2^5.\nonumber \]
Припускаючи, що цей шаблон триває, ми можемо записати\(n^{\text{th}}\) термін у послідовності за явною формулою\(a_n=2^n.\) Використовуючи це позначення, ми можемо записати цю послідовність як
\[\{2^n\}^∞_{n=1}\nonumber \]
або
\[\{2^n\}.\nonumber \]
Як варіант, ми можемо описати цю послідовність по-іншому. Оскільки кожен член вдвічі перевищує попередній термін, ця послідовність може бути визначена рекурсивно, виражаючи\(n^{\text{th}}\) термін\(a_n\) у терміні попереднього терміну\(a_{n−1}\). Зокрема, ми можемо визначити цю послідовність як послідовність,\(\{a_n\}\) де\(a_1=2\) і для всіх\(n≥2\), кожен член a визначається співвідношенням повторення.
\[a_n=2a_{n−1}. \nonumber \]
Нескінченна послідовність\(\{a_n\}\) - це впорядкований список номерів виду
\(a_1,\,a_2,\,…,\,a_n,\,….\)
\(n\)Індексний індекс називається індексною змінною послідовності. Кожне число\(a_n\) є терміном послідовності. Іноді послідовності визначаються явними формулами, у цьому випадку\(a_n=f(n)\) для деякої функції\(f(n)\) визначено над додатними цілими числами. В інших випадках послідовності визначаються за допомогою рекуррентного відношення. У рекуррентному відношенні один член (або більше) послідовності задається явно, а наступні терміни визначаються через більш ранні терміни послідовності.
Зауважте, що індекс не повинен починатися з,\(n=1\) але може починатися з інших цілих чисел. Наприклад, послідовність, задана явною формулою,\(a_n=f(n)\) може починатися з\(n=0\), і в цьому випадку послідовність буде
\[a_0,\,a_1,\,a_2,….\nonumber \]
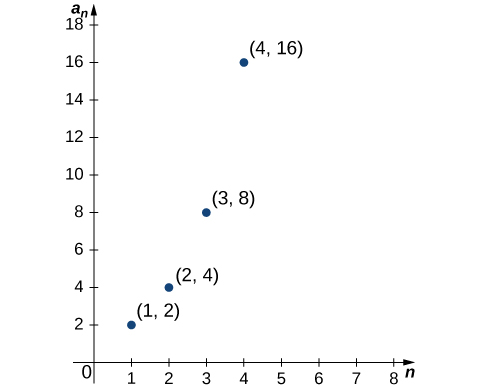
Аналогічно, для послідовності, визначеної рекуррентним зв'язком, термін\(a_0\) може бути вказаний явно, а терміни\(a_n\) для\(n≥1\) можуть бути визначені термінами\(a_{n−1}\). Оскільки послідовність\(\{a_n\}\) має рівно одне значення для кожного додатного цілого числа\(n\), її можна описати як функцію, доменом якої є набір натуральних чисел. В результаті має сенс обговорити графік послідовності. Графік послідовності\(\{a_n\}\) складається з усіх точок\((n,a_n)\) для всіх натуральних чисел n\({2^n}\).
Часто зустрічаються два типи послідовностей і їм даються спеціальні назви: арифметичні послідовності і геометричні послідовності. В арифметичній послідовності різниця між кожною парою послідовних членів однакова. Для прикладу розглянемо послідовність
\[3,\,7,\,11,\,15,1\,9, \,\ldots\nonumber \]
Ви можете бачити, що різниця між кожною послідовною парою термінів є\(4\). Припускаючи, що ця закономірність триває, ця послідовність є арифметичною послідовністю. Його можна описати за допомогою рекуррентного відношення
\[\begin{cases}a_1=3\\a_n=a_{n−1}+4, \text{ for }\ n≥2\end{cases}.\nonumber \]
Зверніть увагу, що
\[a_2=3+4\nonumber \]
\[a_3=3+4+4=3+2⋅4\nonumber \]
\[a_4=3+4+4+4=3+3⋅4.\nonumber \]
Таким чином, послідовність також може бути описана за допомогою явної формули.
\[a_n=3+4(n−1)=4n−1.\nonumber \]
Взагалі, арифметична послідовність - це будь-яка послідовність виду\(a_n=cn+b.\)
У геометричній послідовності співвідношення кожної пари послідовних членів однакове. Для прикладу розглянемо послідовність
\[2,\,−\dfrac{2}{3},\,\dfrac{2}{9},\,−\dfrac{2}{27},\,\dfrac{2}{81},….\nonumber \]
Ми бачимо, що відношення будь-якого терміна до попереднього терміну є\(−\dfrac{1}{3}\). Якщо припустити, що цей візерунок продовжується, ця послідовність є геометричною послідовністю. Його можна визначити рекурсивно як
\[ a_1=2\nonumber \]
\[a_n=−\dfrac{1}{3}⋅a_{n−1}, \text{ for }\ n≥2.\nonumber \]
Як варіант, так як
\[ \begin{align*} a_2 &=−\dfrac{1}{3}⋅2 \\[4pt] a_3 &=\left(−\dfrac{1}{3}\right)\left(−\dfrac{1}{3}\right)(2)=\left(−\dfrac{1}{3}\right)^2⋅2 \\[4pt] a_4 &= \left(−\dfrac{1}{3}\right)\left(−\dfrac{1}{3}\right)\left(−\dfrac{1}{3}\right)(2)=\left(−\dfrac{1}{3}\right)^3⋅2,\end{align*} \nonumber \]
ми бачимо, що послідовність можна описати, використовуючи явну формулу
\[a_n=2 \left(−\dfrac{1}{3}\right)^{n−1}.\nonumber \]
Послідовність\(\{2^n\}\), про яку ми говорили раніше, являє собою геометричну послідовність, де відношення будь-якого члена до попереднього члена дорівнює\(2\). Взагалі, геометрична послідовність - це будь-яка послідовність форми\(a_n=cr^n\).
Для кожної з наступних послідовностей знайдіть явну формулу для\(n^{\text{th}}\) терміна послідовності.
- \(−\dfrac{1}{2},\dfrac{2}{3},−\dfrac{3}{4},\dfrac{4}{5},−\dfrac{5}{6},…\)
- \(\dfrac{3}{4},\dfrac{9}{7},\dfrac{27}{10},\dfrac{81}{13},\dfrac{243}{16},…\).
Рішення
а. по-перше, зверніть увагу, що послідовність чергується від негативної до позитивної. Непарні долі в послідовності негативні, а парні - позитивні. Тому\(n^{\text{th}}\) термін включає в себе коефіцієнт\((−1)^n\). Далі розглянемо послідовність чисельників\({1,2,3,…}\) і послідовність знаменників\({2,3,4,…}\). Ми бачимо, що обидві ці послідовності є арифметичними послідовностями. \(n^{\text{th}}\)Термін в послідовності чисельників є\(n\), а\(n^{\text{th}}\) термін в послідовності знаменників -\(n+1\). Тому послідовність може бути описана явною формулою
\[a_n=\dfrac{(−1)^nn}{n+1}. \nonumber \]
б Послідовність чисельників\(3,9,27,81,243,…\) - це геометрична послідовність. Чисельником\(n^{\text{th}}\) терміна є\(3^n\) Послідовність знаменників\(4,7,10,13,16,…\) - це арифметична послідовність. Знаменником\(n^{\text{th}}\) терміна є\(4+3(n−1)=3n+1.\) Отже, ми можемо описати послідовність за явною формулою\(a_n=\dfrac{3^n}{3n+1.}\)
Знайти явну формулу для\(n^{\text{th}}\) терміна послідовності\(\left\{\dfrac{1}{5},−\dfrac{1}{7},\dfrac{1}{9},−\dfrac{1}{11},…\right\}.\)
- Підказка
-
Знаменники утворюють арифметичну послідовність.
- Відповідь
-
\(a_n=\dfrac{(−1)^{n+1}}{3+2n}\)
Для кожної з наступних рекурсивно визначених послідовностей знайдіть явну формулу послідовності.
- \(a_1=2, a_n=−3a_{n−1}\)для\(n≥2\)
- \(a_1=\left(\dfrac{1}{2}\right), a_n=a_{n−1}+\left(\dfrac{1}{2}\right)^n\)для\(n≥2\)
Рішення
а. виписуючи перші кілька термінів, ми маємо
\[ \begin{align*} a_1 &=2 \\[4pt] a_2 &=−3a_1=−3(2)\\[4pt] a_3 &=−3a_2=(−3)^22\\[4pt] a_4 &=−3a_3=(−3)^32.\end{align*}\]
Загалом,
\(a_n=2(−3)^{n−1}.\)
б. випишіть перші кілька термінів:
\(a_1=\dfrac{1}{2}\)
\(a_2=a_1+\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2}+\dfrac{1}{4}=\dfrac{3}{4}\)
\(a_3=a_2+\left(\dfrac{1}{2}\right)^3=\dfrac{3}{4}+\dfrac{1}{8}=\dfrac{7}{8}\)
\(a_4=a_3+\left(\dfrac{1}{2}\right)^4=\dfrac{7}{8}+\dfrac{1}{16}=\dfrac{15}{16}\).
З цієї закономірності виведемо явну формулу
\(a_n=\dfrac{2^n−1}{2^n}=1−\dfrac{1}{2^n}\).
Знайдіть явну формулу для послідовності, визначеної рекурсивно таким чином, що\(a_1=−4\) і\(a_n=a_{n−1}+6\).
- Підказка
-
Це арифметична послідовність.
- Відповідь
-
\(a_n=6n−10\)
Межа послідовності
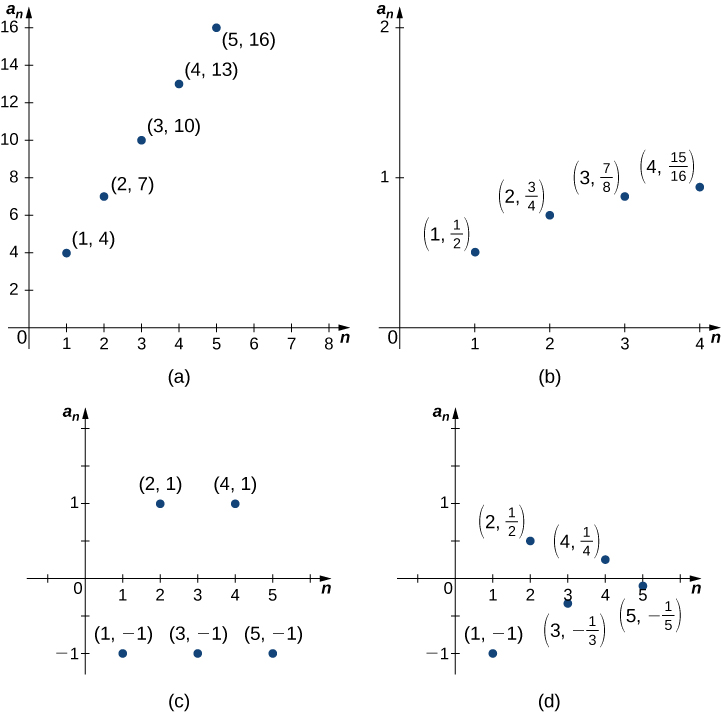
Фундаментальне питання, яке виникає щодо нескінченних послідовностей, - це поведінка термінів, оскільки\(n\) стає більшим. Оскільки послідовність - це функція, визначена на додатних цілих числах, має сенс обговорити межу членів як\(n→∞\). Наприклад, розглянемо наступні чотири послідовності та їх різну поведінку як\(n→∞\) (рис.\(\PageIndex{2}\)):
- \(\{1+3n\}=\{4,7,10,13,…\}.\)Терміни\(1+3n\) стають довільно великими як\(n→∞\). У цьому випадку ми говоримо, що\(1+3n→∞\) як\(n→∞.\)
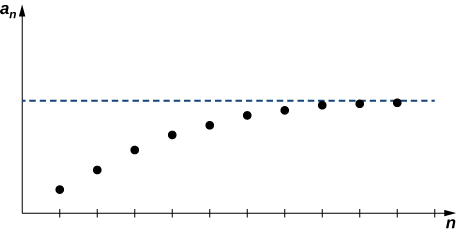
- \(\left\{1− \left(\dfrac{1}{2}\right) ^n\right\}=\left\{ \dfrac{1}{2} ,\dfrac{3}{4},\dfrac{7}{8},\dfrac{15}{16}\,…\right\}.\)Терміни\(1−\left(\dfrac{1}{2}\right)^n→1\) як\(n→∞.\)
- \(\{(−1)^n\}=\{−1,1,−1,1,…\}.\)Терміни чергуються, але не наближаються до одного єдиного значення як\(n→∞.\)
- \(\left\{\dfrac{(−1)^n}{n}\right\}=\left\{−1,\dfrac{1}{2},−\dfrac{1}{3},\dfrac{1}{4},…\right\}.\)Терміни чергуються і для цієї послідовності, але\(\dfrac{(−1)^n}{n}→0\) як\(n→∞.\)
З цих прикладів ми бачимо кілька можливостей поведінки термінів послідовності як\(n→∞\). У двох послідовностях терміни наближаються до кінцевого числа, як і\(n→∞.\) в інших двох послідовностях, терміни цього не роблять. Якщо терміни послідовності наближаються до скінченного числа\(L\) як\(n→∞\), ми говоримо, що послідовність є збіжною послідовністю, а дійсне число L - межа послідовності. Тут ми можемо дати неформальне визначення.
Задано послідовність,\({a_n},\) якщо терміни можуть стати довільно близькими до скінченного числа,\(L\) оскільки n стає досить великим, ми говоримо, що\(\{a_n\}\) це збіжна послідовність і\(L\) є межею послідовності. В даному випадку пишемо
\[\lim_{n→∞}a_n=L. \nonumber \]
Якщо послідовність\(\{a_n\}\) не збігається, ми говоримо, що це розбіжна послідовність.
З малюнка ми бачимо, що терміни в послідовності\(\left\{1− \left(\dfrac{1}{2}\right)^n\right\}\) стають довільно близькими до того\(1\), як\(n\) стає дуже великим. Робимо висновок, що\(\left\{1−\left(\dfrac{1}{2}\right)^n\right\}\) є збіжною послідовністю і її межа є\(1\). На відміну від Figure, ми бачимо, що терміни в послідовності не\(1+3n\) наближаються до кінцевого числа, оскільки\(n\) стає більше. Ми говоримо, що\(\{1+3n\}\) це розбіжна послідовність.
У неформальному визначенні межі послідовності ми використовували терміни «довільно близько» і «досить великий». Хоча ці фрази допомагають проілюструвати значення сходиться послідовності, вони кілька розпливчасті. Якщо бути більш точним, тепер ми представимо більш формальне визначення межі для послідовності і покажемо ці ідеї графічно на малюнку.
Послідовність\(\{a_n\}\) сходиться до дійсного числа\(ε>0\),\(L\) якщо для всіх існує ціле число\(N\) таке, що для всіх\(n ≥ N\)\(|a_n−L| < ε\). Число\(L\) - межа послідовності і пишемо
\[\lim_{n→∞}a_n = L \text{ or } a_n→L. \nonumber \]
У цьому випадку ми говоримо, що послідовність\(\{a_n\}\) є збіжною послідовністю. Якщо послідовність не сходиться, це розбіжна послідовність, і ми говоримо, що межі не існує.
Ми зауважимо, що збіжність або розбіжність послідовності\(\{a_n\}\) залежить тільки від того, що відбувається з термінами\(a_n\) як\(n→∞\). Тому, якщо скінченне число членів\(b_1,b_2,…,b_N\) ставиться перед тим,\(a_1\) щоб створити нову послідовність
\[b_1,\,b_2,\,…,\,b_N,\,a_1,\,a_2,\,…,\nonumber \]
ця нова послідовність сходиться, якщо\(\{a_n\}\) сходиться і розходиться, якщо\(\{a_n\}\) розходиться. Далі, якщо послідовність\(\{a_n\}\) сходиться до\(L\), ця нова послідовність також сходиться до\(L\).
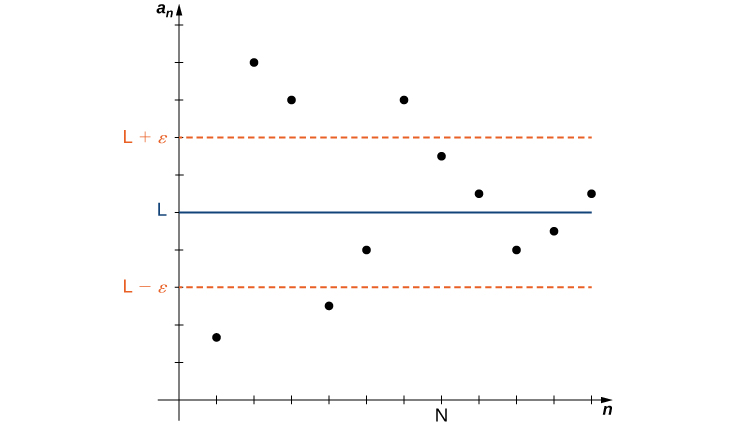
Як визначено вище, якщо послідовність не сходиться, вона називається дивергентною послідовністю. Наприклад, послідовності\(\{1+3n\}\) і\(\left\{(−1)^n\right\}\) показані на малюнку розходяться. Однак різні послідовності можуть розходитися по-різному. Послідовність\(\left\{(−1)^n\right\}\) розходиться тому, що терміни чергуються між\(1\) і\(−1\), але не наближаються до одного значення як\(n→∞\). З іншого боку, послідовність\(\{1+3n\}\) розходиться, оскільки терміни\(1+3n→∞\) як\(n→∞\). Ми говоримо, що послідовність\(\{1+3n\}\) розходиться до нескінченності і пишемо\(\displaystyle \lim_{n→∞}(1+3n)=∞\). Важливо визнати, що це позначення не передбачає обмеження послідовності\(\{1+3n\}\) існує. Послідовність, по суті, розходиться. Написання про те, що межа - нескінченність, призначене лише для того, щоб надати більше інформації про те, чому послідовність розходиться. Послідовність також може розходитися до негативної нескінченності. Наприклад, послідовність\(\{−5n+2\}\) розходиться до негативної нескінченності\(−5n+2→−∞\), тому що як\(n→−∞\). Ми пишемо це як\(\displaystyle \lim_{n→∞}(−5n+2)=→−∞.\)
Оскільки послідовність - це функція, область якої є набором натуральних чисел, ми можемо використовувати властивості меж функцій, щоб визначити, чи збігається послідовність. Наприклад, розглянемо послідовність\(\{a_n\}\) і пов'язану функцію,\(f\) визначену для всіх позитивних дійсних чисел, такі, що\(f(n)=a_n\) для всіх цілих чисел\(n≥1\). Оскільки область послідовності є підмножиною області\(f\), якщо\(\displaystyle \lim_{x→∞}f(x)\) існує, то послідовність сходиться і має однакову межу. Наприклад, розглянемо послідовність\(\left\{\dfrac{1}{n}\right\}\) і пов'язану з нею функцію\(f(x)=\dfrac{1}{x}\). Оскільки функція,\(f\) визначена на всіх дійсних числах,\(x>0\) задовольняє\(f(x)=\dfrac{1}{x}→0\) as\(x→∞\), послідовність\(\left\{\dfrac{1}{n}\right\}\) повинна задовольняти\(\dfrac{1}{n}→0\) як\(n→∞.\)
Розглянемо послідовність\(\{a_n\}\) таку, що\(a_n=f(n)\) для всіх\(n≥1\). Якщо існує дійсне число\(L\) таке, що
\[\lim_{x→∞}f(x)=L, \nonumber \]
потім\(\{a_n\}\) сходиться і
\[\lim_{n→∞}a_n=L. \nonumber \]
Ми можемо використовувати цю теорему\(\displaystyle \lim_{n→∞}r^n\) для оцінки\(0≤r≤1\). Наприклад, розглянемо послідовність\(\left\{(1/2)^n\right\}\) і пов'язану з нею експоненціальну функцію\(f(x)=(1/2)^x\). Так як\(\displaystyle \lim_{x→∞}(1/2)^x=0\), робимо висновок, що послідовність\(\left\{(1/2)^n\right\}\) сходиться і її межа є\(0\). Аналогічно, для будь-якого дійсного числа\(r\) таке\(0≤r<1\), що\(\displaystyle \lim_{x→∞}r^x=0\), а значить і послідовність\(\left\{r^n\right\}\) сходиться. З іншого боку, якщо\(r=1\)\(\displaystyle \lim_{x→∞}r^x=1\), то і значить межа послідовності\(\left\{1^n\right\}\) є\(1\). Якщо\(r>1\)\(\displaystyle \lim_{x→∞}r^x=∞\), а значить, ми не можемо застосувати цю теорему. Однак у цьому випадку, так само, як функція\(r^x\) зростає без обмежень, як\(n→∞\), терміни\(r^n\) в послідовності стають довільно великими як\(n→∞\), і ми робимо висновок, що послідовність\(\left\{r^n\right\}\) розходиться до нескінченності якщо\(r>1\).
Підсумовуємо ці результати щодо геометричної послідовності\({r^n}\):
\(r^n→0\)якщо\(0<r<1\)
\(r^n→1\)якщо\(r=1\)
\(r^n→∞\)якщо\(r>1\).
Пізніше в цьому розділі ми розглянемо випадок, коли\(r<0\).
Ми зараз розглянемо трохи складніші послідовності. Наприклад, розглянемо\(\left\{(2/3)^n+(1/4)^n\right\}.\) послідовність Терміни в цій послідовності складніші, ніж інші послідовності, про які ми говорили, але, на щастя, межа цієї послідовності визначається межами двох послідовностей\(\left\{(2/3)^n\right\}\) і\(\left\{(1/4)^n\right\}\). Як ми описуємо в наступних алгебраїчних граничних законів, оскільки\(\left\{(2/3)^n\right\}\) і\(\left\{1/4)^n\right\}\) обидва сходяться до\(0\), послідовність\(\left\{(2/3)^n+(1/4)^n\right\}\) сходиться до\(0+0=0\). Так само, як ми змогли оцінити межу за участю алгебраїчної комбінації функцій\(f\) і, дивлячись\(g\) на межі\(f\) і\(g\) (див. Вступ до меж), ми можемо оцінити межу послідовності, чиї терміни є алгебраїчними комбінаціями\(a_n\) і \(b_n\)оцінюючи межі\(\{a_n\}\) і\(\{b_n\}\).
Задані послідовності\(\{a_n\}\)\(\{b_n\}\) і і будь-яке дійсне число\(c\), якщо існують константи\(A\) і\(B\) такі, що\(\displaystyle \lim_{n→∞}a_n=A\) і\(\displaystyle \lim_{n→∞}b_n=B\), то
- \(\displaystyle \lim_{n→∞}c=c\)
- \(\displaystyle \lim_{n→∞}ca_n=c\lim_{n→∞}a_n=cA\)
- \(\displaystyle \lim_{n→∞}(a_n±b_n)=\lim_{n→∞}a_n±\lim_{n→∞}b_n=A±B\)
- \(\displaystyle \lim_{n→∞}(a_n⋅b_n)=\big(\lim_{n→∞}a_n\big)⋅\big(\lim_{n→∞}b_n\big)=A⋅B\)
- \(\displaystyle \lim_{n→∞}\left(\dfrac{a_n}{b_n}\right)=\dfrac{\lim_{n→∞}a_n}{\lim_{n→∞}b_n}=\dfrac{A}{B}\), за умови\(B≠0\) і кожного\(b_n≠0.\)
Доводимо частину iii.
Нехай\(ϵ>0\). Так як\(\displaystyle \lim_{n→∞}a_n=A\), існує постійне натуральне число\(N_1\) таке, що для всіх\(n≥N_1\). Так як\(\displaystyle \lim_{n→∞}b_n=B\), існує константа\(N_2\) така, що\(|b_n−B|<ε/2\) для всіх\(n≥N_2\). \(N\)Дозволяти бути найбільшим з\(N_1\) і\(N_2\). Тому для всіх\(n≥N\),\(|(a_n+b_n)−(A+B)|≤|a_n−A|+|b_n−B|<\dfrac{ε}{2}+\dfrac{ε}{2}=ε\).
□
Алгебраїчні граничні закони дозволяють оцінити межі для багатьох послідовностей. Для прикладу розглянемо послідовність\(a_n={\dfrac{1}{n^2}}\). Як було показано раніше,\(\displaystyle \lim_{n→∞}\dfrac{1}{n}=0\). Аналогічно, для будь-якого натурального цілого\(k\), ми можемо зробити висновок, що
\[\lim_{n→∞}\dfrac{1}{n^k}=0. \nonumber \]
У наступному прикладі ми використовуємо цей факт разом із граничними законами для оцінки лімітів для інших послідовностей.
Для кожної з наступних послідовностей визначте, сходиться чи ні послідовність. Якщо вона сходиться, знайдіть її межу.
- \(\left\{5−\dfrac{3}{n^2}\right\}\)
- \(\left\{\dfrac{3n^4−7n^2+5}{6−4n^4}\right\}\)
- \(\left\{\dfrac{2^n}{n^2}\right\}\)
- \(\left\{\left(1+\dfrac{4}{n}\right)^n\right\}\)
Рішення
а Ми це знаємо\(\displaystyle \lim_{n→∞}\dfrac{1}{n}=0\). Використовуючи цей факт, робимо висновок, що
\(\displaystyle \lim_{n→∞}\dfrac{1}{n^2}=\lim_{n→∞}\dfrac{1}{n}.\lim_{n→∞}\dfrac{1}{n}=0.\)
Тому,
\(\displaystyle \lim_{n→∞}\left(5−\dfrac{3}{n^2}\right)=\lim_{n→∞}5−3\lim_{n→∞}\dfrac{1}{n^2}=5−3.0=5.\)
Послідовність сходиться і її межа дорівнює 5.
б. факторинг\(n^4\) з чисельника і знаменника і використовуючи граничні закони вище, ми маємо
\ [\ почати {вирівнювати*}\ lim_ {n→∞}\ dfrac {3n^4−7n^2+5} {6−4n^4} &=\ lim_ {n→∞}\ dfrac {3−\ dfrac {7} {n^2} +\ dfrac {5} {n^4}} {\ dfrac {6} {n^2} 4} −4}\\ [5пт]
&=\ dfrac {\ lim_ {n→∞} (3−\ dfrac {7} {n^2} +\ dfrac {5} {n^4})} {\ lim_ {n→∞} (\ dfrac {6} {n^4} −4)}\\ [5pt]
&=\ dfrac {\ lim_ {n→∞} (3) −\ lim_ {n→∞}\ dfrac {7} {n^2} +\ lim_ {n→∞}\ dfrac {5} {n^4}} {\ lim_ {n→∞}\ dfrac {6} {n^4} −\ lim_ {n→∞} (4)}\\ [5пт]
&=\ dfrac {\ lim_ {n→∞} (3) −7⋅\ lim_ {n→∞} 1} {n^2} +5⋅\ lim_ {n→∞}\ dfrac {1} {n^4}} {6⋅\ lim_ {n→∞}\ dfrac {1} {n^4} −\ lim_ {n→∞} (4)}\\ [5pt]
&=\ dfrac {3−7⋅0+5⋅0} {6⋅0+0} −4} =−\ dfrac {3} {4}. \ end {вирівнювати*}\]
Послідовність сходиться і її межа є\(−3/4\).
c Розглянемо пов'язану функцію,\(f(x)=2^x/x^2\) визначену на всіх дійсних числах\(x>0\). Оскільки\(2^x→∞\) і\(x^2→∞\) як\(x→∞\), застосовуйте правило L'Hôpital і пишіть
\ [\ begin {align*}\ lim_ {x→∞}\ dfrac {2^x} {x^2} &=\ lim_ {x→∞}\ dfrac {2x\ ln2} {2x} &\ text {Візьміть похідні від чисельника та знаменника.}\\ [5pt]
&=\ lim_ {x→∞}\ dfrac {2^x (\ ln2) ^2} {2} &\ text {Візьміть похідні ще раз.}\\ [5pt]
&=∞. \ end {вирівнювати*}\]
Робимо висновок, що послідовність розходиться.
d Розглянемо функцію,\(f(x)=\left(1+\dfrac{4}{x}\right)^x\) визначену на всіх дійсних числах\(x>0\). Ця функція має невизначену форму\(1^∞\) як\(x→∞.\) Let
\(\displaystyle y=\lim_{x→∞}\left(1+\dfrac{4}{x}\right)^x\).
Тепер взявши натуральний логарифм обох сторін рівняння, отримаємо
\(\displaystyle \ln(y)=\ln\left[\lim_{x→∞}\left(1+\dfrac{4}{x}\right)^x\right]\).
Оскільки функція\(f(x)=\ln(x)\) є безперервною у своїй області, ми можемо змінити межу та натуральний логарифм. Тому,
\(\displaystyle \ln(y)=\lim_{x→∞}\left[\ln\left(1+\dfrac{4}{x}\right)^x\right]\).
Використовуючи властивості логарифмів, запишемо
\(\displaystyle \lim_{x→∞}\left[\ln\left(1+\dfrac{4}{x}\right)^x\right]=\lim_{x→∞}x\ln\left(1+\dfrac{4}{x}\right)\).
Оскільки права частина цього рівняння має невизначену форму\(∞⋅0\), перепишіть його як дріб, щоб застосувати правило L'Hôpital. Напишіть
\(\displaystyle \lim_{x→∞}x\ln\left(1+\dfrac{4}{x}\right)=\lim_{x→∞}\dfrac{\ln\left(1+4/x\right)}{1/x}\).
Оскільки права частина тепер у невизначеній формі 0/0, ми можемо застосувати правило L'Hôpital. Ми робимо висновок, що
\(\displaystyle \lim_{x→∞}\dfrac{\ln(1+4/x)}{1/x}=\lim_{x→∞}\dfrac{4}{1+4/x}=4.\)
Тому\(\ln(y)=4\) і\(y=e^4\). Тому, оскільки\(\displaystyle \lim_{x→∞}\left(1+\dfrac{4}{x}\right)^x=e^4\), можна зробити висновок, що послідовність\(\left\{\left(1+\dfrac{4}{n}\right)^n\right\}\) сходиться до\(e^4\).
Розглянемо послідовність\(\left\{(5n^2+1)/e^n\right\}.\) Визначте, сходиться чи ні послідовність. Якщо вона сходиться, знайдіть її межу.
- Підказка
-
Використовуйте правило L'Hôpital.
- Відповідь
-
Послідовність сходиться, і її межа дорівнює\(0\)
Нагадаємо, що якщо\(f\) є безперервною функцією при\(L\) значенні, то\(f(x)→f(L)\) як\(x→L\). Ця ідея стосується і послідовностей. Припустимо\(a_n→L\), послідовність, а функція\(f\) є безперервною в\(L\). Потім\(f(a_n)→f(L)\). Ця властивість часто дозволяє нам знаходити межі для складних послідовностей. Для прикладу розглянемо послідовність\(\sqrt{5−\dfrac{3}{n^2}}\). З Прикладу a. ми знаємо послідовність\(5−\dfrac{3}{n^2}→5\). Оскільки\(\sqrt{x}\) є безперервною функцією при\(x=5\),
\[\lim_{n→∞}\sqrt{5−\dfrac{3}{n^2}}=\sqrt{\lim_{n→∞}(5−\dfrac{3}{n^2})}=\sqrt{5}.\nonumber \]
Розглянемо послідовність\(\{a_n\}\) і припустимо, що існує дійсне число,\(L\) таке, що послідовність\(\{a_n\}\) сходиться до\(L\). Припустимо,\(f\) це неперервна функція в\(L\). Потім існує\(N\) таке ціле число, яке\(f\) визначається при всіх значеннях a for\(n≥N\), а послідовність\(\{f(a_n)\}\) сходиться до\(f(L)\) (рис.\(\PageIndex{4}\)).
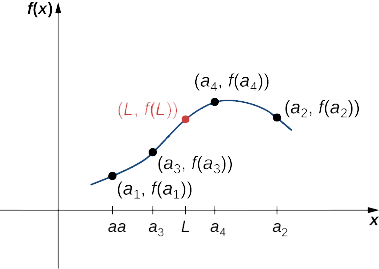
Нехай\(ϵ>0.\) Оскільки\(f\) безперервно в\(L\), існує\(δ>0\) таке, що\(|f(x)−f(L)|<ε\) якщо\(|x−L|<δ\). Оскільки послідовність\(\{a_n\}\) сходиться до\(L\), існує\(N\) така, що\(|a_n−L|<δ\) для всіх\(n≥N\). Тому для всіх\(n≥N\)\(|a_n−L|<δ\), що має на увазі\(|f(a_n)−f(L)|<ε\). Робимо висновок, що послідовність\(\{f(a_n)\}\) сходиться до\(f(L)\).
□
Визначте, чи\(\left\{\cos(3/n^2)\right\}\) сходиться послідовність. Якщо вона сходиться, знайдіть її межу.
Рішення:
Оскільки послідовність\(\left\{3/n^2\right\}\) сходиться до\(0\) і\(\cos x\) є безперервною в\(x=0\), можна зробити висновок, що послідовність\(\left\{\cos(3/n^2)\right\}\) сходиться і
\(\displaystyle \lim_{n→∞}\cos\left(\dfrac{3}{n^2}\right)=\cos 0=1.\)
Визначте, чи\(\left\{\sqrt{\dfrac{2n+1}{3n+5}}\right\}\) сходиться послідовність. Якщо вона сходиться, знайдіть її межу.
- Підказка
-
Розглянемо послідовність\(\left\{\dfrac{2n+1}{3n+5}\right\}.\)
- Відповідь
-
Послідовність сходиться, і її межа є\(\sqrt{2/3}\).
Інша теорема, що включає межі послідовностей, є розширенням теореми стискання для меж, розглянутих у Введенні до меж.
Розглянемо послідовності\(\{a_n\}, \, \{b_n\},\) і\(\{c_n\}\). Припустимо, існує ціле число\(N\) таке, що
\(a_n≤b_n≤c_n\)для всіх\(n≥N.\)
Якщо існує дійсне число\(L\) таке, що
\[\lim_{n→∞}a_n=L=\lim_{n→∞}c_n, \nonumber \]
потім\(\{b_n\}\) сходиться і\(\displaystyle \lim_{n→∞}b_n=L\) (рис.\(\PageIndex{5}\)).
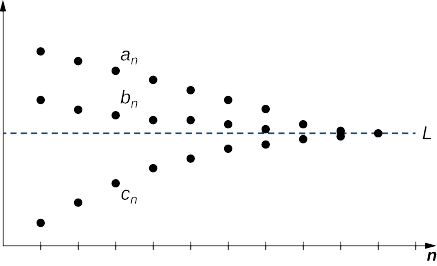
Нехай\(ε>0.\) Оскільки послідовність\(\{a_n\}\) сходиться до\(L\), існує ціле число\(N_1\) таке, що\(|a_n−L|<ε\) для всіх\(n≥N_1\). Аналогічно, оскільки\(\{c_n\}\) сходиться до\(L\), існує ціле число\(N_2\) таке, що\(|c_n−L|<ε\) для всіх\(n≥N_2\). За припущенням існує ціле число\(N\) таке, що\(a_n≤b_n≤c_n\) для всіх\(n≥N\). \(M\)Дозволяти бути найбільшим з\(N_1,\, N_2\), і\(N\). Ми повинні показати це\(|b_n−L|<ε\) для всіх\(n≥M\). Для всіх\(n≥M\),
\[−ε<−|a_n−L|≤a_n−L≤b_n−L≤c_n−L≤|c_n−L|<ε\nonumber \]
Тому\(−ε<b_n−L<ε,\) і робимо висновок, що\(|b_n−L|<ε\) для всіх\(n≥M\), і робимо висновок, що послідовність\({b_n}\) сходиться до\(L\).
□
Скористайтеся теоремою стискання, щоб знайти межу кожної з наступних послідовностей.
- \(\left\{\dfrac{\cos\, n}{n^2}\right\}\)
- \(\left\{\left(−\dfrac{1}{2}\right)^n\right\}\)
Рішення
а Оскільки\(−1≤\cos n≤1\) для всіх цілих чисел\(n\), ми маємо
\(−\dfrac{1}{n^2} ≤ \dfrac{\cos n}{n^2}≤\dfrac{1}{n^2}.\)
Оскільки\(−1/n^2→0\) і\(1/n^2→0\), ми робимо висновок, що\(\cos n/n^2→0\) також.
б. з тих пір
\(−\dfrac{1}{2^n} ≤ \left(−\dfrac{1}{2}\right)^n ≤ \dfrac{1}{2^n}\)
для всіх натуральних чисел,\(n, \, −1/2^n→0\) і\(1/2^n→0,\) ми можемо зробити висновок, що\((−1/2)^n→0.\)
Знайти\(\displaystyle \lim_{n→∞}\dfrac{2n−\sin\, n}{n}.\)
- Підказка
-
Використовуйте той факт, що\(−1≤\sin n≤1.\)
- Відповідь
-
\(2\)
Використовуючи ідею з Прикладу,\(\PageIndex{5}\) b ми робимо висновок, що\(r^n→0\) для будь-якого дійсного числа r такого\(r<−1\), що\(−1<r<0.\) If, послідовність\({r^n}\) розходиться, тому що терміни коливаються і стають довільно великими за величиною. Якщо\(r=−1\), послідовність\({r^n}={(−1)^n}\) розходиться, як обговорювалося раніше. Ось короткий опис властивостей геометричних послідовностей.
\(r^n→0 \text{ if } |r|<1\)
\(r^n→1\text{ if } r=1\)
\(r^n→∞\text{ if } r>1\)
\(\left\{r^n\right\} \text{ diverges if } r≤−1\)
Обмежені послідовності
Тепер звернемо увагу на одну з найважливіших теорем, що включають послідовності: теорему про монотонну збіжність. Перш ніж викладати теорему, потрібно ввести деяку термінологію і мотивацію. Ми починаємо з визначення того, що означає для послідовності, яка буде обмежена.
Послідовність\(\{a_n\}\) обмежується вище, якщо існує дійсне число,\(M\) таке, що
\(a_n≤M\)
для всіх натуральних чисел\(n\).
Послідовність\(\{a_n\}\) обмежується нижче, якщо існує дійсне число,\(m\) таке, що
\(m≤a_n\)
для всіх натуральних чисел\(n\).
Послідовність\(\{a_n\}\) є обмеженою послідовністю, якщо вона обмежена вище і обмежена нижче.
Якщо послідовність не обмежена, вона є необмеженою послідовністю.
Наприклад, послідовність\(\{1/n\}\) обмежена вище, тому що\(1/n≤1\) для всіх натуральних чисел\(n\). Він також обмежений нижче, тому що\(1/n≥0\) для всіх натуральних чисел\(n\). Отже,\(\{1/n\}\) є обмеженою послідовністю. З іншого боку, розглянемо послідовність\(\left\{2^n\right\}\). Тому що\(2^n≥2\) для всіх\(n≥1\) послідовність обмежена нижче. Однак послідовність не обмежена вище. Отже,\(\left\{2^n\right\}\) є необмеженою послідовністю.
Зараз ми обговорюємо взаємозв'язок між обмеженістю і конвергенцією. Припустимо\(\{a_n\}\), послідовність необмежена. Тоді вона не обмежена вище, або не обмежена нижче, або обидва. У будь-якому випадку існують терміни an, які довільно великі за величиною, оскільки\(n\) стає більшими. В результаті послідовність\(\{a_n\}\) не може сходитися. Тому обмеженість є необхідною умовою для зближення послідовності.
Якщо послідовність\(\{a_n\}\) сходиться, то вона обмежена.
Зауважте, що обмежена послідовність не є достатньою умовою для зближення послідовності. Наприклад, послідовність\(\left\{(−1)^n\right\}\) обмежена, але послідовність розходиться, оскільки послідовність коливається між\(1\)\(−1\) і ніколи не наближається до кінцевого числа. Зараз ми обговоримо достатню (але необов'язкову) умову для зближення обмеженої послідовності.
Розглянемо обмежену послідовність\(\{a_n\}\). Припустимо,\(\{a_n\}\) послідовність збільшується. Тобто,\(a_1≤a_2≤a_3….\) Оскільки послідовність збільшується, терміни не коливаються. Тому є дві можливості. Послідовність могла розходитися до нескінченності, або вона могла сходитися. Однак, оскільки послідовність обмежена, вона обмежена вище, і послідовність не може розходитися до нескінченності. Робимо висновок, що\(\{a_n\}\) сходиться. Для прикладу розглянемо послідовність
\[\left\{\dfrac{1}{2},\,\dfrac{2}{3},\,\dfrac{3}{4},\,\dfrac{4}{5},\,…\right\}. \nonumber \]
Оскільки ця послідовність збільшується і обмежується вище, вона сходиться. Далі розглянемо послідовність
\[\left\{2,\,0,\,3,\,0,\,4,\,0,\,1,\,−\dfrac{1}{2},\,−\dfrac{1}{3},\,−\dfrac{1}{4},\,…\right\}. \nonumber \]
Незважаючи на те, що послідовність не збільшується для всіх значень\(n\), ми бачимо, що\(−1/2<−1/3<−1/4<⋯\). Тому, починаючи з восьмого члена\(a_8=−1/2\), послідовність збільшується. У цьому випадку ми говоримо, що послідовність з часом збільшується. Так як послідовність обмежена вище, вона сходиться. Також вірно, що якщо послідовність зменшується (або врешті-решт зменшується) і обмежена нижче, вона також сходиться.
\(\{a_n\}\)Послідовність збільшується для всіх,\(n≥n_0\) якщо
\(a_n≤a_{n+1}\)для всіх\(n≥n_0\).
Послідовність\(\{a_n\}\) зменшується для всіх,\(n≥n_0\) якщо
\(a_n ≥ a_{n+1}\)для всіх\(n≥n_0\).
Послідовність\(\{a_n\}\) - це монотонна послідовність для всіх,\(n≥n_0\) якщо вона збільшується для всіх\(n≥n_0\) або зменшується для всіх\(n≥n_0\).
Тепер ми маємо необхідні визначення для констатації теореми монотонної збіжності, яка дає достатню умову збіжності послідовності.
Якщо\(\{a_n\}\) є обмеженою послідовністю і існує додатне ціле число\(n_0\) таке, що\(\{a_n\}\) є монотонним для всіх\(n≥n_0\), то\(\{a_n\}\) сходиться.
Доказ цієї теореми виходить за рамки цього тексту. Замість цього ми надаємо графік, щоб інтуїтивно показати, чому ця теорема має сенс (рис.\(\PageIndex{6}\)).
У наступному прикладі показано, як теорема монотонної збіжності може бути використана для доведення збіжності послідовності.
Для кожної з наступних послідовностей використовуйте теорему монотонної збіжності, щоб показати послідовність збіжності та знайти її межу.
- \(\left\{\dfrac{4^n}{n!}\right\}\)
- \(\{a_n\}\)визначено рекурсивно такий, що
\(a_1=2\) і\(a_{n+1}=\dfrac{a_n}{2}+\dfrac{1}{2a_n}\) для всіх\(n≥2.\)
Рішення
а. виписуючи перші кілька термінів, ми бачимо, що
\(\left\{\dfrac{4^n}{n!}\right\}=\left\{4,\,8,\,\dfrac{32}{3},\,\dfrac{32}{3},\,\dfrac{128}{15},\,…\right\}.\)
Спочатку терміни збільшуються. Однак після третього терміну терміни зменшуються. Фактично терміни зменшуються для всіх\(n≥3\). Ми можемо показати це наступним чином.
\(a_{n+1}=\dfrac{4^{n+1}}{(n+1)!}=\dfrac{4}{n+1}⋅\dfrac{4^n}{n!}=\dfrac{4}{n+1}⋅a_n≤a_n\)якщо\(n≥3.\)
Тому послідовність зменшується для всіх\(n≥3\). Далі послідовність обмежується нижче тим,\(0\) що\(4n/n!≥0\) для всіх натуральних чисел\(n\). Тому за теоремою монотонної збіжності послідовність сходиться.
Щоб знайти межу, скористаємося тим, що послідовність сходиться і нехай\(\displaystyle L=\lim_{n→∞}a_n\). Тепер відзначимо це важливе спостереження. Розглянемо\(\displaystyle \lim_{n→∞}a_{n+1}\). Так як
\(\{a_{n+1}\}=\{a_2,\,a_3,\,a_4,\,…\},\)
єдина відмінність між послідовностями\(\{a_{n+1}\}\) і\(\{a_n\}\) полягає в тому, що\(\{a_{n+1}\}\) опускає перший член. Оскільки скінченне число членів не впливає на збіжність послідовності,
\(\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}a_n=L.\)
Поєднання цього факту з рівнянням
\(a_{n+1}=\dfrac{4}{n+1}a_n\)
і беручи межу обох сторін рівняння
\(\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}\dfrac{4}{n+1}a_n\),
можна зробити висновок, що
\(L=0⋅L=0.\)
б. виписуючи перші кілька термінів,
\(\left\{2,\,\dfrac{5}{4},\,\dfrac{41}{40},\,\dfrac{3281}{3280},\,…\right\}.\)
ми можемо здогадатися, що послідовність зменшується і обмежена нижче\(1\). Щоб показати, що послідовність обмежена нижче\(1\), ми можемо показати, що
\(\dfrac{a_n}{2}+\dfrac{1}{2a_n}≥1.\)
Щоб показати це, спочатку перепишіть
\(\dfrac{a_n}{2}+\dfrac{1}{2a_n}=\dfrac{a^2_n+1}{2a_n}\).
Так як\(a_1>0\) і\(a_2\) визначається як сума позитивних членів,\(a_2>0.\) аналогічно всім термінам\(a_n>0\). Тому,
\(\dfrac{a^2n+1}{2a_n}≥1\)
якщо і тільки якщо
\(a^2_n+1≥2a_n\).
Переписування нерівності\(a^2_n+1≥2a_n\) як\(a^2_n−2a_n+1≥0\), так і з використанням того, що
\(a^2_n−2a_n+1=(a_n−1)^2≥0\)
оскільки квадрат будь-якого дійсного числа є невід'ємним, можна зробити висновок, що
\(\dfrac{a^n}{2}+\dfrac{1}{2a_n}≥1.\)
Щоб показати, що послідовність зменшується, ми повинні показати, що\(a_{n+1}≤a_n\) для всіх\(n≥1\). Так як\(1≤a^2_n\), випливає, що
\(a^2_n+1≤2a^2_n\).
Розділивши обидві сторони на\(2a_n\), отримуємо
\(\dfrac{a_n}{2}+\dfrac{1}{2a_n}≤a_n.\)
Використовуючи визначення\(a_{n+1}\), робимо висновок, що
\(a_{n+1}=\dfrac{a_n}{2}+\dfrac{1}{2a_n}≤a_n\).
Оскільки\(\{a_n\}\) обмежений нижче і зменшується, за теоремою монотонної збіжності він сходиться.
Щоб знайти межу, нехай\(\displaystyle L=\lim_{n→∞}a_n\). Потім за допомогою рекуррентних відносин і той факт\(\displaystyle \lim_{n→∞}a_n=\lim_{n→∞}a_{n+1}\), що, ми маємо
\(\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}(\dfrac{a_n}{2}+\dfrac{1}{2a_n})\),
і тому
\(L=\dfrac{L}{2}+\dfrac{1}{2L}\).
Помноживши обидві сторони цього рівняння на\(2L\), приходимо до рівняння
\(2L^2=L^2+1\).
Вирішуючи це рівняння,\(L,\) ми робимо висновок про те\(L^2=1\), що має на увазі\(L=±1\). Так як всі терміни позитивні, то межа\(L=1\).
Розглянемо послідовність,\(\{a_n\}\) визначену рекурсивно таким\(a_1=1\) чином,\(a_n=a_{n−1}/2\). Використовуйте теорему про збіжність монотонних, щоб показати, що ця послідовність сходиться і знайти її межу.
- Підказка
-
Показати послідовність зменшується і обмежена нижче.
- Відповідь
-
\(0\).
Числа Фібоначчі визначаються рекурсивно послідовністю\(\left\{F_n\right\}\), де\(F_0=0, \, F_1=1\) і для\(n≥2,\)
\(F_n=F_{n−1}+F_{n−2}.\)
Тут ми розглянемо властивості чисел Фібоначчі.
1. Випишіть перші двадцять чисел Фібоначчі.
2. Знайдіть замкнуту формулу для послідовності Фібоначчі, виконавши наступні кроки.
a Розглянемо рекурсивно визначену послідовність\({x_n}\), де\(x_0=c\) і\(x_{n+1}=ax_n\). Показати, що цю послідовність можна описати замкнутою формулою\(x_n=ca^n\) для всіх\(n≥0.\)
б. використовуючи результат з частини а. в якості мотивації, шукати рішення рівняння
\(F_n=F_{n−1}+F_{n−2}\)
форми\(F_n=cλ^n\). Визначити, які два значення для\(λ\) дозволять\(F_n\) задовольнити це рівняння.
c Розглянемо два рішення з частини б.:\(λ_1\) і\(λ_2\). Нехай\(F_n=c_1λ_1^n+c_2λ_2^n\). Використовуйте початкові умови\(F_0\) і\(F_1\) для визначення значень для констант\(c_1\)\(c_2\) і запишіть замкнуту формулу\(F_n\).
3. Скористайтеся відповіддю в 2 с., щоб показати, що
\[\lim_{n→∞}\dfrac{F_{n+1}}{F_n}=\dfrac{1+\sqrt{5}}{2}.\nonumber \]
Число\(ϕ=(1+\sqrt{5})/2\) відоме як золоте перетин (Малюнок і Малюнок).


Ключові концепції
- Для визначення збіжності послідовності, заданої явною формулою\(a_n=f(n)\), використовуються властивості меж для функцій.
- Якщо\(\{a_n\}\) і\(\{b_n\}\) є збіжними послідовностями, які сходяться до\(A\) і\(B,\) відповідно, і\(c\) є будь-яким дійсним числом, то послідовність\(\{ca_n\} \) сходиться до\(c\cdot A,\) послідовності\(\{a_n±b_n\}\)\(\{a_n\cdot b_n\}\) сходяться до\(A±B,\) послідовності сходяться до\(A⋅B,\) і послідовність\(\{a_n/b_n\}\) сходиться до\(A/B,\) наданої\(B≠0.\)
- Якщо послідовність обмежена і монотонна, то вона сходиться, але не всі збігаються послідовності монотонні.
- Якщо послідовність необмежена, вона розходиться, але не всі розбіжні послідовності необмежені.
- Геометрична послідовність\(\left\{r^n\right\}\) сходиться тоді і тільки якщо\(|r|<1\) або\(r=1\).
Глосарій
- арифметична послідовність
- послідовність, в якій різниця між кожною парою послідовних членів однакова називається арифметичною послідовністю
- обмежений вище
- послідовність\(\{a_n\}\) обмежена вище, якщо існує константа\(M\) така, що\(a_n≤M\) для всіх натуральних чисел\(n\)
- обмежений нижче
- послідовність\(\{a_n\}\) обмежена нижче, якщо існує константа\(M\) така, що\(M≤a_n\) для всіх натуральних чисел\(n\)
- обмежена послідовність
- послідовність\(\{a_n\}\) обмежена, якщо існує константа\(M\) така, що\(|a_n|≤M\) для всіх натуральних чисел\(n\)
- конвергентна послідовність
- збіжна послідовність - це послідовність,\(\{a_n\}\) для якої існує дійсне число\(L\)\(a_n\) таке, яке довільно близьке до тих\(L\) пір, поки\(n\) є досить великим
- розбіжна послідовність
- послідовність, яка не є сходженням є розходиться
- явна формула
- послідовність може бути визначена явною формулою, такою, що\(a_n=f(n)\)
- геометрична послідовність
- послідовність,\(\{a_n\}\) в якій співвідношення\(a_{n+1}/a_n\) однакове для всіх натуральних чисел\(n\) називається геометричною послідовністю
- змінна індексу
- індекс, який використовується для визначення термінів у послідовності, називається індексом
- межа послідовності
- дійсне число,\(L\) до якого сходиться послідовність, називається межею послідовності
- монотонна послідовність
- зростаюча або зменшується послідовність
- рецидивний зв'язок
- рекуррентне відношення - це зв'язок, в якому термін\(a_n\) в послідовності визначається з точки зору більш ранніх термінів у послідовності
- послідовність
- упорядкований список номерів форми\(a_1,\,a_2,\,a_3,\,…\) - це послідовність
- термін
- число\(a_n\) в послідовності\(\{a_n\}\) називається\(n^{\text{th}}\) терміном послідовності
- необмежена послідовність
- послідовність, яка не обмежена, називається необмеженою
