Skip to main content
LibreTexts - Ukrayinska

1.4: Основна факторизація

  1. Last updated
  2. Save as PDF
  • Page ID
    57233

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    У заяві 3 · 4 = 12 число 12 називається твором, в той час як 3 і 4 називаються факторами.

    Приклад 1

    Знайти всі цілі числові фактори 18.

    Рішення

    Нам потрібно знайти всі цілі числові пари, добуток яких дорівнює 18. На думку спадають такі пари.

    1 · 18 = 18 і 2 · 9 = 18 і 3 · 6 = 18.

    Значить, фактори 18 є (по порядку) 1, 2, 3, 6, 9 і 18.

    Вправа

    Знайти всі цілі числові фактори 21.

    Відповідь

    1, 3, 7 і 21

    подільність

    У прикладі 1 ми побачили 3 · 6 = 18, зробивши 3 і 6 коефіцієнти 18. Оскільки ділення є оберненою множенням, тобто ділення на число скасовує множення цього числа, це відразу забезпечує

    18 ÷ 6 = 3 і 18 ÷ 3 = 6.

    Тобто 18 ділиться на 3 і 18 ділиться на 6. Коли ми говоримо, що 18 ділиться на 3, ми маємо на увазі, що коли 18 ділиться на 3, залишається нульовий залишок.

    Ділимий

    Нехай a і b будуть цілими числами. Тоді a ділиться на b, якщо і тільки якщо залишок дорівнює нулю, коли a ділиться на b. У цьому випадку ми говоримо, що «b - дільник a».

    Приклад 2

    Знайти всі цілі дільники числа 18.

    Рішення

    У прикладі 1 ми побачили, що 3 · 6 = 18. Тому 18 ділиться як на 3, так і на 6 (18 ÷ 3 = 6 і 18 ÷ 6 = 3). Значить, коли 18 ділиться на 3 або 6, залишок дорівнює нулю. Тому 3 і 6 - дільники 18. Відзначаючи інші продукти в прикладі 1, повний список дільників 18 становить 1, 2, 3, 6, 9 та 18.

    Вправа

    Знайти всі цілі дільники числа 21.

    Відповідь

    1, 3, 7 і 21.

    Приклад 1 і Приклад 2 показують, що при роботі з цілими числами слова коефіцієнт і дільник взаємозамінні.

    Фактори та дільники

    Якщо c = a · b, то a і b називаються множниками c. Обидва a і b також називаються дільниками c.

    Тести на подільність

    Існує ряд дуже корисних тестів на подільність.

    Ділиться на 2. Якщо ціле число закінчується на 0, 2, 4, 6 або 8, то число називається парним числом і ділиться на 2. Прикладами парних чисел є 238 і 1,246 (238 ÷ 2 = 119 і 1, 246 ÷ 2 = 623). Число, яке не є парним, називається непарним числом. Прикладами непарних чисел є 113 і 2,339.

    Ділиться на 3. Якщо сума цифр цілого числа ділиться на 3, то саме число ділиться на 3. Прикладом може служити 141. Сума цифр 1 + 4 + 1 = 6, яка ділиться на 3. Тому 141 також ділиться на 3 (141 ÷ 3 = 47).

    Ділиться на 4. Якщо число, представлене останніми двома цифрами цілого числа, ділиться на 4, то саме число ділиться на 4. Прикладом є 11,524. Останні дві цифри представляють 24, яке ділиться на 4 (24 ÷ 4 = 6). Отже, 11 524 ділиться на 4 (11 524 ÷ 4 = 2, 881).

    Ділимо на 5. Якщо ціле число закінчується нулем або 5, то число ділиться на 5. Прикладами є 715 і 120 (715÷5 = 143 і 120÷5 = 24).

    Ділимо на 6. Якщо ціле число ділиться на 2 і на 3, то воно ділиться на 6. Прикладом може служити 738. По-перше, 738 рівний і ділиться на 2. По-друге, 7+3+8=18, що ділиться на 3. Значить, 738 ділиться на 3. Оскільки 738 ділиться як на 2, так і на 3, він ділиться на 6 (738 ÷ 6 = 123).

    Ділимо на 8. Якщо число, представлене останніми трьома цифрами цілого числа, ділиться на 8, то саме число ділиться на 8. Прикладом може служити 73 024. Останні три цифри представляють число 24, яке ділиться на 8 (24÷8 = 3). Таким чином, 73 024 також ділиться на 8 (73, 024÷8 = 9, 128).

    Ділимо на 9. Якщо сума цифр цілого числа ділиться на 9, то саме число ділиться на 9. Прикладом може служити 117. Сума цифр 1 + 1 + 7 = 9, яка ділиться на 9. Значить, 117 ділиться на 9 (117 ÷ 9 = 13).

    Прості числа

    Почнемо з визначення простого числа.

    Просте число

    Ціле число (крім 1) є простим числом, якщо його єдиними множниками (дільниками) є 1 і саме. Аналогічно, число є простим тоді і лише тоді, коли воно має рівно два множники (дільники).

    Приклад 3

    Які з цілих чисел 12, 13, 21 і 37 є простими числами?

    Рішення

    • Коефіцієнтами (дільниками) 12 є 1, 2, 3, 4, 6 і 12. Отже, 12 не є простим числом.
    • Коефіцієнтами (дільниками) 13 є 1 і 13. Оскільки його єдиними дільниками є 1 і сам, 13 є простим числом.
    • Коефіцієнтами (дільниками) 21 є 1, 3, 7 і 21. Отже, 21 не є простим числом.
    • Коефіцієнтами (дільниками) 37 є 1 і 37. Оскільки його єдиними дільниками є 1 і сам, 37 є простим числом.

    Вправа

    Які з цілих чисел 15, 23, 51 і 59 є простими числами?

    Відповідь

    23 і 59

    Приклад 4

    Перерахуйте всі прості числа менше 20.

    Рішення

    Простими числами менше 20 є 2, 3, 5, 7, 11, 13, 17 і 19.

    Ви спробуєте!

    Перерахуйте всі прості числа менше 100.

    Складені числа

    Якщо ціле число не є простим числом, то воно називається складовим числом.

    Приклад 5

    Ціле число 1,179 просте або складене?

    Рішення

    Зверніть увагу, що 1 + 1 + 7 + 9 = 18, що ділиться як на 3, так і на 9. Отже, 3 і 9 обидва дільники 1,179. Тому 1179 - це складене число.

    Вправа

    Ціле число 2,571 просте або складене?

    Відповідь

    Композитний

    Факторні дерева

    Зараз ми навчимося виражати складене число як унікальний добуток простих чисел. Найпопулярнішим пристроєм для досягнення цієї мети є дерево факторів.

    Приклад 6

    Експрес 24 як добуток простих множників.

    Рішення

    Ми використовуємо факторне дерево, щоб розбити 24 на добуток простих чисел.

    Знімок екрана 2019-08-07 в 8.00.41 PM.png

    На кожному рівні дерева розбийте поточне число на добуток двох факторів. Процес завершується, коли всі «обведені листя» внизу дерева є простими числами. Розставляючи фактори в «обведеному листі» по порядку,

    24 = 2 · 2 · 2 · 3.

    Остаточна відповідь не залежить від вибору продукту, зробленого на кожному рівні дерева. Ось ще один підхід.

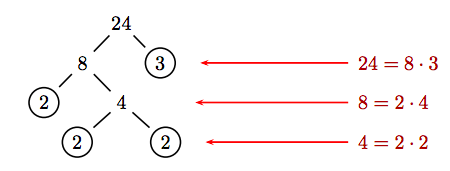
    Знімок екрана 2019-08-07 в 8.00.48 PM.png

    Остаточну відповідь можна знайти, включивши всі фактори з «обведеного листя» в кінці кожної гілки дерева, що дає однаковий результат, а саме 24 = 2 · 2 · 2 · 3.

    Альтернативний підхід

    Деякі надають перевагу багаторазовому діленню на 2, поки результат не буде ділитися на 2. Потім спробуйте багаторазово розділити на наступний простий, поки результат не буде ділитися на це просте. Процес завершується, коли останній результуючий частка дорівнює числу 1.

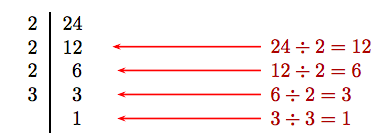
    Знімок екрана 2019-08-07 в 8.00.56 PM.png

    Перший стовпець розкриває просту факторизацію; тобто 24 = 2 · 2 · 2 · 3.

    Вправа

    Експрес 36 як добуток простих множників.

    Відповідь

    2 · 2 · 3 · 3.

    Той факт, що альтернативний підхід у прикладі 6 дав той же результат, є значним.

    Унікальна теорема факторизації

    Кожне ціле число може бути однозначно враховано як добуток простих чисел.

    Цей результат гарантує, що якщо прості множники впорядковані від найменших до найбільших, кожен отримає однаковий результат при розбиванні числа на добуток простих множників.

    Показники

    Почнемо з визначення експоненціального виразу.

    Експоненти

    Вираз a m визначається як середнє

    \( a^{m}=\underbrace{a \cdot a \cdot \ldots \cdot a}_{m \text { times }}\)

    Число a називається основою експоненціального виразу, а число m називається показником. Показник m говорить нам повторити базу a як множник m раз.

    Приклад 7

    Оцініть 2, 5, 2, 3, і 5 2.

    Рішення

    • У випадку з 2 5 ми маємо

    2 5 = 2 · 2 · 2 · 2

    = 32.

    • У випадку з 3 3, ми маємо

    3 = 3 · 3 · 3

    = 27.

    • У випадку з 5 2, ми маємо

    5 2 = 5 · 5

    = 25.

    Вправа

    Оцініть: 3 5.

    Відповідь

    243.

    Приклад 8

    Висловіть рішення на прикладі 6 в компактному вигляді за допомогою експонентів.

    Рішення

    У прикладі 6 ми визначили просту факторизацію 24.

    24 = 2 · 2 · 2 · 3

    Тому що 2 · 2 · 2=23, ми можемо написати це більш компактно.

    24 = 2 3 · 3

    Вправа

    Просте коефіцієнт 54.

    Відповідь

    2 · 3 · 3 · 3

    Приклад 9

    Оцініть вираз 2 3 · 3 2 · 5 2.

    Рішення

    Спочатку підніміть кожен коефіцієнт до заданого показника, потім виконайте множення по порядку (зліва направо).

    2 3 · 3 2 · 5 2 = 8 · 9 · 25

    = 72 · 25

    = 1800

    Вправа

    Оцініть: 3 3 · 5 2.

    Відповідь

    675

    Додаток

    Квадрат - це прямокутник з чотирма рівними сторонами.

    Площа площі

    Давайте представляємо довжину кожної сторони квадрата.

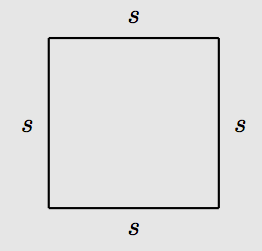
    Знімок екрана 2019-08-07 о 8.08.27 PM.png

    Оскільки квадрат також є прямокутником, ми можемо знайти площу квадрата, помноживши його довжину та ширину. Однак в цьому випадку довжина і ширина обидва рівні s, тому A = (s) (s) (s) = s 2. Значить, формула для площі квадрата

    А = s 2.

    приклад 10

    Край квадрата дорівнює 13 сантиметрам. Знайдіть площу квадрата.

    Рішення

    Підставте s = 13 см в формулу площі.

    А = с 2

    = (13 см) 2

    = (13 см) (13 см)

    = 169 см 2

    Значить, площа квадрата становить 169 см 2; тобто 169 квадратних сантиметрів.

    Вправа

    Край квадрата становить 15 метрів. Знайдіть площу квадрата.

    Відповідь

    225 квадратних метрів

    Вправи

    У вправах 1-12 знайти всі дільники заданого числа.

    1. 30

    2. 19

    3. 83

    4. 51

    5. 91

    6. 49

    7. 75

    8. 67

    9. 64

    10. 87

    11. 14

    12. 89

    У вправах 13-20 яке з наступних чисел не ділиться на 2?

    13. 117, 120, 342, 230

    14. 310, 157, 462, 160

    15. 30, 22, 16, 13

    16. 382, 570, 193, 196

    17. 105, 206, 108, 306

    18. 60, 26, 23, 42

    19. 84, 34, 31, 58

    20. 66, 122, 180, 63

    У Вправах 21-28 яке з наступних чисел не ділиться на 3?

    21. 561, 364, 846, 564

    22. 711, 850, 633, 717

    23. 186, 804, 315, 550

    24. 783, 909, 504, 895

    25. 789, 820, 414, 663

    26. 325, 501, 945, 381

    27. 600, 150, 330, 493

    28. 396, 181, 351, 606

    У Вправах 29-36 яке з наступних чисел не ділиться на 4?

    29. 3797, 7648, 9944, 4048

    30. 1012, 928, 717, 1592

    31. 9336, 9701, 4184, 2460

    32. 2716, 1685, 260, 9788

    33. 9816, 7517, 8332, 7408

    34. 1788, 8157, 7368, 4900

    35. 1916, 1244, 7312, 7033

    36. 740, 5844, 2545, 9368

    У Вправах 37-44 яке з наступних чисел не ділиться на 5?

    37. 8920, 4120, 5285, 9896

    38. 3525, 7040, 2185, 2442

    39. 8758, 3005, 8915, 3695

    40. 340, 1540, 2485, 2543

    41. 2363, 5235, 4145, 4240

    42. 9030, 8000, 5445, 1238

    43. 1269, 5550, 4065, 5165

    4. 7871, 9595, 3745, 480

    У вправах 45-52 яке з наступних чисел не ділиться на 6?

    45. 328, 372, 90, 528

    46. 720, 288, 148, 96

    47. 744, 174, 924, 538

    48. 858, 964, 930, 330

    49. 586, 234, 636, 474

    50. 618, 372, 262, 558

    51. 702, 168, 678, 658

    52. 780, 336, 742, 312

    У вправах 53-60, яке з наступних чисел не ділиться на 8?

    53. 1792, 8216, 2640, 5418

    54. 2168, 2826, 1104, 2816

    5. 8506, 3208, 9016, 208

    56. 2626, 5016, 1392, 1736

    57. 4712, 3192, 2594, 7640

    58. 9050, 9808, 8408, 7280

    59. 9808, 1232, 7850, 7912

    60. 3312, 1736, 9338, 3912

    У вправах 61-68, яке з наступних чисел не ділиться на 9?

    61. 477, 297, 216, 991

    62. 153, 981, 909, 919

    63. 153, 234, 937, 675

    64. 343, 756, 927, 891

    65. 216, 783, 594, 928

    66. 504, 279, 307, 432

    67. 423, 801, 676, 936

    68. 396, 684, 567, 388

    У вправах 69-80 визначте задане число як просте, складене або ні інше.

    69. 19

    70. 95

    71. 41

    72. 88

    73. 27

    74. 61

    75. 91

    76. 72

    77. 21

    78. 65

    79. 23

    80. 36

    У вправах 81-98 знайти просту факторизацію натурального числа.

    81. 224

    82. 320

    83. 108

    84. 96

    85. 243

    86. 324

    87. 160

    88. 252

    89. 32

    90. 128

    91. 360

    92. 72

    93. 144

    94. 64

    95. 48

    96. 200

    97. 216

    98. 392

    У вправах 99-110 обчислити точне значення заданого експоненціального виразу.

    99. 5 2 · 4 1

    100. 2 3 · 4 1

    101. 0 1

    102. 1 3

    103. 3 · 0 2

    104. 3 3 · 2 2

    105. 4 1

    106. 5 2

    107. 4 3

    108. 4 2

    109. 3 3 · 1 2

    110. 5 2 · 2 3

    У вправах 111-114 знайдіть площу квадрата з заданою стороною.

    111. 28 дюймів

    112. 31 дюйм

    113. 22 дюйма

    114. 13 дюймів

    Створіть дерева факторів для кожного числа у Вправи 115-122. Запишіть просту факторизацію для кожного числа в компактному вигляді, використовуючи показники.

    115. 12

    116. 18

    117. 105

    118. 70

    119. 56

    120. 56

    121. 72

    122. 270

    123. Сито Ератосфена. Ця вправа вводить Сито Ератосфена, стародавній алгоритм знаходження простих чисел менше певного числа n, вперше створений грецьким математиком Ератосфаном. Розглянемо сітку цілих чисел від 2 до 100.

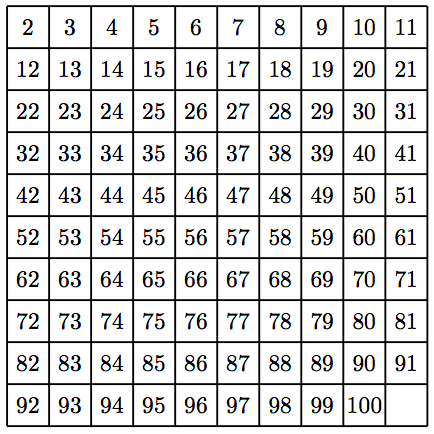
    Знімок екрана 2019-08-07 в 8.53.48 PM.png

    Щоб знайти прості числа менше 100, дійте наступним чином.

    i) Викреслити всі кратні 2 (4, 6, 8 і т.д.)

    ii) Наступне число списку, яке не було викреслено, є простим числом.

    iii) Викреслити зі списку всі кратні числу, яке ви визначили на кроці (ii).

    iv) Повторюйте кроки (ii) та (iii), поки ви більше не зможете вдарити більше кратні.

    v) Усі невизначені числа в списку є простими числами.

    Відповіді

    1. 1, 2, 3, 5, 6, 10, 15, 30

    3. 1, 83

    5. 1, 7, 13, 91

    7. 1, 3, 5, 15, 25, 75

    9. 1, 2, 4, 8, 16, 32, 64

    11. 1, 2, 7, 14

    13. 117

    15. 13

    17. 105

    19. 31

    21. 364

    23. 550

    25. 820

    27. 493

    29. 3797

    31. 9701

    33. 7517

    35. 7033

    37. 9896

    39. 8758

    41. 2363

    43. 1269

    45. 328

    47. 538

    49. 586

    51. 658

    53. 5418

    55. 8506

    57. 2594

    59. 7850

    61. 991

    63. 937

    65. 928

    67. 676

    69. прем'єр

    71. прем'єр

    73. композит

    75. композит

    77. композит

    79. прем'єр

    81. 2 · 2 · 2 · 2 · 7

    83. 2 · 2 · 3 · 3

    85. 3 · 3 · 3 · 3

    87. 2 · 2 · 2 · 2 · 5

    89. 2 · 2 · 2 · 2

    91. 2 · 2 · 2 · 3 · 5

    93. 2 · 2 · 2 · 2 · 3 · 3

    95. 2 · 2 · 2 · 3

    97. 2 · 2 · 2 · 3 · 3

    99. 100

    101. 0

    103. 0

    105. 4

    107. 64

    109. 27

    111. 784 у 2

    113. 484 у 2

    115. 12 = 22 · 3

    117. 105 = 3 · 5 · 7

    119. 56 = 23 · 7

    121. 72 = 23 · 32

    123. Незабитими числами є прості числа: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97