2: Спеціальна структура та рішення ОДУ
- Page ID
- 61198
Послідовна тема у всіх ОДА полягає в тому, що «особлива структура» рівнянь може виявити розуміння природи розв'язків. Тут ми розглянемо дуже основне і важливе властивість автономних рівнянь:
«Часові зрушення розв'язків автономних ОД також є розв'язками ОДА (але з іншою початковою умовою)».
Зараз ми покажемо, як в цьому переконатися.
Протягом цього курсу ми будемо вважати, що існування та унікальність розв'язків тримається на області та часовому інтервалі, достатньому для наших аргументів та обчислень.
Починаємо з встановлення налаштування. Розглянуто автономне векторне поле, визначене на\(\mathbb{R}^n\):
\[\dot{x} = f(x) \quad x(0) = x_{0}, \quad x \in \mathbb{R}^n, \label{2.1}\]
з розчином позначається:
\[x(t, 0, x_{0}), \,x(0, 0, x_{0}) = x_{0}.\]
Тут ми беремо початковий час, щоб бути\(t_{0} = 0\). Незабаром ми побачимо, що для автономних рівнянь це можна зробити без втрати спільності. Тепер вибираємо\(s \in \mathbb{R}\) (\(s \ne 0\), який слід розглядати як фіксовану константу). Ми повинні показати наступне:
\[\dot{x}(t+s) = f(x(t+s))\label{2.2}\]
Це те, що ми маємо на увазі під фразою тимчасові зрушення рішень. Це співвідношення випливає відразу з розрахунку правила ланцюга:
\[\frac{d}{dt} = \frac{d}{d(t+s)} \frac{d(t+s)}{dt} = \frac{d}{d(t+s)}. \label{2.3}\]
Нарешті, нам потрібно визначити початкову умову для зрушеного за часом рішення. Для оригінального рішення у нас є:
\[x(t, 0, x_{0}), x(0, 0, x_{0}) = x_{0}, \label{2.4}\]
і за час зрушеного рішення у нас є:
\[x(t + s, 0, x_{0}), x(s, 0, x_{0}). \label{2.5}\]
Саме з цієї причини, без втрати спільності, для автономних векторних полів ми можемо взяти початковий час\(t_{0} = 0\). Це дозволяє спростити аргументи в позначеннях для розв'язків автономних векторних полів, т\(x(0, 0, x_{0}) = x(0, x_{0}) = x_{0}\).\(x(t, 0, x_{0}) \equiv x(t, x_{0})\) Е.
Приклад\(\PageIndex{5}\): The time-shift property of autonomous vector fields
Розглянемо наступне одновимірне автономне векторне поле:
\[\dot{x} = \lambda x, x(0) = x_{0}, x \in \mathbb{R}, \lambda \in \mathbb{R}. \nonumber\]
Рішення дається:
\[x(t, 0, x_{0}) = x(t, x_{0}) = e^{\lambda t}x_{0}. \nonumber\]
Час зсунутого рішення задається:
\[x(t+s, x_{0}) = e^{\lambda (t+s)}x_{0}. \nonumber\]
Ми бачимо, що це рішення ОДА з наступними розрахунками:
\[\frac{d}{dt}x(t+s, x_{0}) = \lambda e^{\lambda (t+s)}x_{0} = \lambda x(t+s, x_{0}), \nonumber\]
з початковим станом:
\[x(s, x_{0}) = e^{\lambda s}x_{0}. \nonumber\]
Підводячи підсумок, ми бачимо, що розв'язки автономних векторних полів задовольняють наступним трьом властивостям:
- \(x(0, x_{0}) = x_{0}\)
- \(x(t, x_{0})\)знаходиться\(C^{r}\) в\(x_{0}\)
- \(x(t+s, x_{0}) = x(t, x(s, x_{0}))\)
Власність один якраз відображає прийняті нами позначення. Property 2 - це твердження властивостей, що виникають внаслідок існування та унікальності рішень. Властивість 3 використовує дві характеристики рішень. Одним з них є властивість «зсуву часу» для автономних векторних полів, які ми довели. Інша - «унікальність рішень», оскільки ліва сторона та права частина Property 3 задовольняють однаковій початковій умові при t = 0.
Ці три властивості є визначальними властивостями потоку, тобто a. Іншими словами, ми розглядаємо рішення як визначення карти точок у фазовому просторі. Властивість групи виникає з властивості 3, тобто властивості зсуву часу. Для того, щоб підкреслити цю властивість «карти фазового простору», введемо загальне позначення для потоку наступним чином:
\[x(t, x_{0}) \equiv \phi_{t}(\cdot) \nonumber\]
де «·» в аргументі\(\phi_{t}(\cdot)\) відображає той факт, що потік є функцією на фазовому просторі. За допомогою цього позначення три властивості потоку записуються наступним чином:
- \(\phi_{0}(\cdot)\)це карта ідентичності.
- \(\phi_{t}(\cdot)\)\(C^r\)припадає на кожну т.
- \(\phi_{t+s}(\cdot) = \phi_{t} \circ \phi_{s}(\cdot)\)
Ми часто використовуємо словосполучення «потік, що генерується (автономним) векторним полем». Автономний знаходиться в дужках, оскільки розуміється, що коли ми розглядаємо потоки, ми розглядаємо рішення автономних векторних полів. Це пов'язано з тим, що неавтономні векторні поля не обов'язково задовольняють властивість зсуву у часі, як ми зараз показуємо на прикладі.
Приклад\(\PageIndex{6}\): An example of a nonautonomous vector field not having the time-shift property
Розглянемо наступне одновимірне векторне поле на\(\mathbb{R}\):
\[\dot{x} = \lambda tx\), \)x(0) = x_{0}, x \in \mathbb{R}\), \(\lambda \in \mathbb{R}. \nonumber\]
Це векторне поле відокремлюється, і рішення легко знайти:
\[x(t, 0, x_{0}) = x_{0}e^{\frac{\lambda}{2}t^2}. \nonumber\]
Час зсунутого «рішення» задається:
\[x(t+s, 0, x_{0}) = x_{0}e^{\frac{\lambda}{2}(t+s)^2}. \nonumber \]
Ми показуємо, що це не задовольняє векторне поле з наступним розрахунком:
\(\frac{d}{dt}x(t+s, 0, x_{0}) = x_{0}e^{\frac{\lambda}{2}(t+s)^2}\lambda (t+s)\).
\(\ne \lambda tx(t+s, 0, x_{0})\).
Можливо, більш простий приклад, який ілюструє, що неавтономні векторні поля не задовольняють властивість зсуву часу, є наступним.
Приклад\(\PageIndex{7}\)
Розглянемо наступне одновимірне неавтономне векторне поле:
\(\dot{x} = e^{t}\),\(x \in \mathbb{R}\).
Рішення дається:
\(x(t) = e^t\).
Легко перевірити, що функція зі зміщенням часу:
\(x(t+s) = e^{t+s}\),
не задовольняє рівнянню.
При вивченні ОДУ певні типи рішень досягли рівня популярності, значною мірою виходячи з їх значущості в додатках. Вони є
- рівноважні рішення,
- періодичні розчини,
- гетероклінічні розчини,
- гомоклінічні рішення.
Визначимо кожен з них.
ВИЗНАЧЕННЯ 8: РІВНОВАГА
Точка в\(x = \bar{x} = \mathbb{R}^n\) фазовому просторі, яка є рішенням ОДА, тобто
\(f(\bar{x}) = 0, f(\bar{x}, t) = 0\),
називається точкою рівноваги.
Наприклад, x = 0 - точка рівноваги для наступних автономних і неавтономних одновимірних векторних полів, відповідно,
- \(\dot{x} = x\),\(x \in \mathbb{R}\),
- \(\dot{x} = tx\),\(x \in \mathbb{R}\).
Періодичне рішення - це просто рішення, яке є періодичним за часом. Його визначення однакове як для автономних, так і для неавтономних векторних полів.
ВИЗНАЧЕННЯ 9: ПЕРІОДИЧНІ РІШЕННЯ
\(x(t, t_{0}, x_{0})\)Розв'язок є періодичним, якщо існує T > 0 такий, що
\(x(t, t_{0}, x_{0}) = x(t+T, t_{0}, x_{0})\)
Гомоклінічні та гетероклінічні розчини мають важливе значення в різних сферах застосування. Їх визначення не настільки просте, як визначення рівноваги та періодичних розв'язків, оскільки вони можуть бути визначені та узагальнені до багатьох різних налаштувань. Ми будемо розглядати тільки ці спеціальні рішення для автономних векторних полів, і розчини гомоклінічних або гетероклінічних до рівноважних розв'язків.
ВИЗНАЧЕННЯ 10 (ГОМОКЛІНІЧНІ ТА ГЕТЕРОКЛІНІЧНІ РОЗЧИНИ)
Припустимо\(\bar{x}_{1}\) і\(\bar{x}_{2}\) є точками рівноваги автономного векторного поля, тобто
\(f(\bar{x}_{1}) = 0\),\(f(\bar{x}_{2}) = 0\).
\(x(t, t_{0}, x_{0})\)Траєкторія, як кажуть, гетероклінічна до\(\bar{x}_{1}\) і\(\bar{x}_{2}\) якщо
\(lim_{t \rightarrow \infty} x(t, t_{0}, x_{0}) = \bar{x}_{2}\),
\[lim_{t \rightarrow -\infty} x(t, t_{0}, x_{0}) = \bar{x}_{1}, \label{2.11}\]
Якщо\(\bar{x}_{1} = \bar{x}_{2}\) траєкторія, як кажуть, гомоклінічна до\(\bar{x}_{1} = \bar{x}_{2}\).
Приклад\(\PageIndex{8}\): equilibrium points and heteroclinic orbits
Розглянемо наступне одновимірне автономне векторне поле на\(\mathbb{R}\):
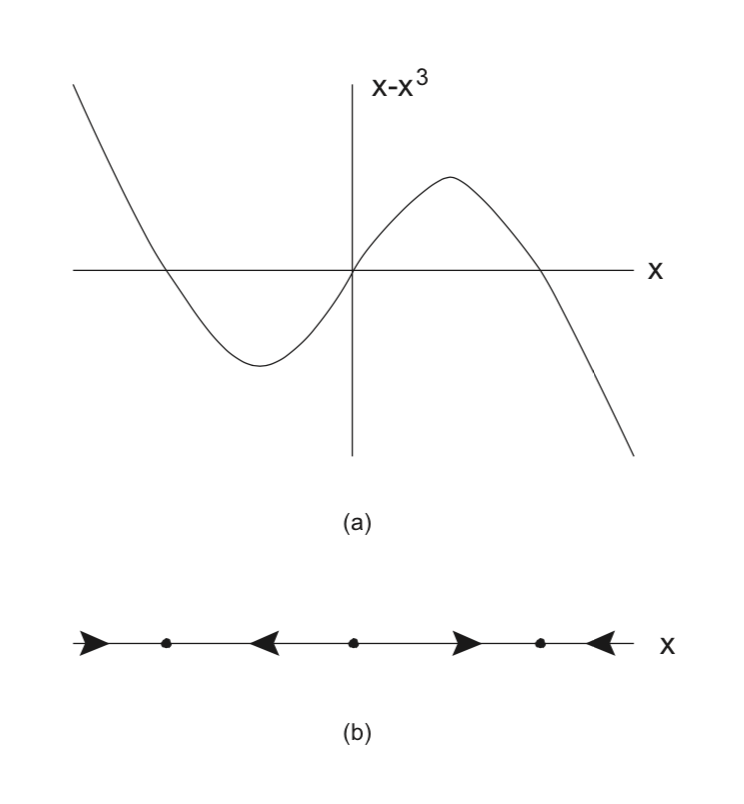
\[\dot{x} = x-x^3 = x(1-x^2), x \in \mathbb{R}. \label{2.12}\]
Це векторне поле має три точки рівноваги на\(x = 0, \pm 1\).
На рис. 2.1 ми показуємо графік векторного поля (2.12) в панелі а) і динаміку фазової лінії в панелі b).
Суцільні чорні точки на панелі b) відповідають точкам рівноваги, і вони, в свою чергу, відповідають нулям векторного поля, показаного на панелі а). Між його нулями векторне поле має фіксований знак (тобто позитивний або негативний), що відповідає тому, що є або збільшенням, або зменшенням. На це вказує напрямок стрілок на панелі б).
Наша дискусія про траєкторії, як і цей приклад, підводить нас до точки, коли закономірно ввести важливе поняття інваріантної множини. Хоча це загальна ідея, яка стосується як автономних, так і неавтономних систем, в цьому курсі ми обговоримо це поняття лише в контексті автономних систем. Відповідно, давайте\(\phi_{t}(\cdot)\) позначимо потік, що генерується автономним векторним полем.
ВИЗНАЧЕННЯ 11: ІНВАРІАНТНИЙ НАБІР
Набір, як кажуть,\(M \subset \mathbb{R}^n\) є інваріантним, якщо
\[x \in M \Rightarrow \phi_{t}(x) \in M\]
\(\forall t\).
Іншими словами, набір є інваріантним (щодо потоку), якщо ви починаєте в наборі, і залишитеся в наборі, назавжди.
Якщо задуматися, то повинно бути зрозуміло, що інваріантні множини - це множини траєкторій. Будь-яка єдина траєкторія - це інваріантна множина. Весь фазовий простір - це інваріантна множина. Найцікавіші випадки - це ті, що «між ними». Також повинно бути зрозуміло, що об'єднання будь-яких двох інваріантних множин також є інваріантною множиною (просто застосувати визначення інваріантної множини до об'єднання двох, або більше, інваріантних множин).
Існують певні ситуації, коли нас цікавлять множини, які є інваріантними лише для позитивного часу — позитивними інваріантними множинами.
ВИЗНАЧЕННЯ 12: ПОЗИТИВНА ІНВАРІАНТНА МНОЖИНА
Безліч\(M \subset \mathbb{R}^n\), як кажуть, позитивний інваріант, якщо
\(x \in M \Rightarrow \phi_{t}(x) \in M\)\(\forall t>0\).
Існує подібне поняття негативних інваріантних множин, але узагальнення цього з визначення позитивних інваріантних множин має бути очевидним, тому виписувати подробиці не будемо.
Що стосується прикладу 8, то три точки рівноваги є інваріантними множинами, а також замкнутими інтервалами\([-1, 0]\) та [0, 1]. Чи існують інші інваріантні набори?
