5: Поведінка поблизу Equilbria - лінеаризація

Приклад$\PageIndex{10}$

Розглянемо наступні лінійні, автономні ОДУ:

$$\begin{pmatrix} {\dot{x_{1}}}\\ {\dot{x_{2}}} \end{pmatrix} = \begin{pmatrix} {2}&{1}\\ {1}&{2} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} \label{5.2}$$

де

$$A = \begin{pmatrix} {2}&{1}\\ {1}&{2} \end{pmatrix}, \label{5.3}$$

Крок 1. Обчислити власні значення A.

Власні значення А, що позначаються$\lambda$, задаються розв'язками характеристичного многочлена:

$det \begin{pmatrix} {2-\lambda}&{1}\\ {1}&{2-\lambda} \end{pmatrix} = (2-\lambda)^2-1 = 0$

$$= \lambda^{2}-4\lambda+3 = 0, \label{5.4}$$

або

$\lambda_{1,2} = 2 \pm \frac{1}{2}\sqrt{16-12} = 3, 1$

Крок 2. Обчислити власні вектори A.

Для кожного власне значення обчислюємо відповідний власнийвектор. Свій вектор, відповідний власному значенню 3, знаходить шляхом розв'язання:

$$\begin{pmatrix} {2}&{1}\\ {1}&{2} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} = 3\begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.5}$$

або

$$2x_{1}+x_{2} = 3x_{1}, \label{5.6}$$

$$x_{1}+2x_{2} = 3x_{2}. \label{5.7}$$

Обидва ці рівняння дають одне і те ж рівняння, оскільки два рівняння залежні:

$$x_{2} = x_{1} \label{5.8}$$ .

Тому приймаємо як власний вектор, відповідний власному значенню 3:

$$\begin{pmatrix} {1}\\ {1} \end{pmatrix} \label{5.9}$$

Далі обчислюємо власне вектор, відповідний власному значенню 1. Це дається розв'язком наступних рівнянь:

$$\begin{pmatrix} {2}&{1}\\ {1}&{2} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} = \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.10}$$

або

$$2x_{1}+x_{2} = x_{1}, \label{5.11}$$

$$x_{1}+2x_{2} = x_{2}. \label{5.12}$$

Обидва ці рівняння дають одне і те ж рівняння:

$$x_{2} = -x_{1}. \label{5.13}$$

Тому візьмемо за свій вектор, відповідний власному значенню:

$$\begin{pmatrix} {1}\\ {-1} \end{pmatrix} \label{5.14}$$

Крок 3. Використовуйте власні вектори A для формування матриці перетворення T.

Для стовпців$T$ візьмемо власні вектори, відповідні власним значенням 1 і 3:

$$T = \begin{pmatrix} {1}&{1}\\ {-1}&{1} \end{pmatrix} \label{5.15}$$

з оберненою заданою:

$$T^{-1} = \frac{1}{2}\begin{pmatrix} {1}&{-1}\\ {1}&{1} \end{pmatrix} \label{5.16}$$

Крок 4. Обчислити$\Lambda = T^{-1}AT$.

У нас є:

$T^{-1}AT = \dfrac{1}{2}\begin{pmatrix} {1}&{-1}\\ {1}&{1} \end{pmatrix} \begin{pmatrix} {2}&{1}\\ {1}&{2} \end{pmatrix} \begin{pmatrix} {1}&{1}\\ {-1}&{1} \end{pmatrix}$

$= \frac{1}{2}\begin{pmatrix} {1}&{-1}\\ {1}&{1} \end{pmatrix} \begin{pmatrix} {1}&{3}\\ {-1}&{3} \end{pmatrix}$

$$= \begin{pmatrix} {1}&{0}\\ {0}&{3} \end{pmatrix} \equiv \Lambda \label{5.17}$$

Тому в$u_{1}-u_{2}$ координатах (5.2) стає:

$$\begin{pmatrix} {\dot{u_{1}}}\\ {\dot{u_{2}}} \end{pmatrix} = \begin{pmatrix} {1}&{0}\\ {0}&{3} \end{pmatrix} \begin{pmatrix} {u_{1}}\\ {u_{2}} \end{pmatrix} \label{5.18}$$

У$u_{1}-u_{2}$ координатах легко помітити, що початок є нестійкою точкою рівноваги.

Крок 5. Обчислити$e^{At} = Te^{\lambda t}T^{-1}$.

У нас є:

$e^{AT} = \frac{1}{2}\begin{pmatrix} {1}&{1}\\ {-1}&{1} \end{pmatrix} \begin{pmatrix} {e^{t}}&{0}\\ {0}&{e^{3t}} \end{pmatrix} \begin{pmatrix} {1}&{-1}\\ {1}&{1} \end{pmatrix}$

$= \frac{1}{2}\begin{pmatrix} {1}&{1}\\ {-1}&{1} \end{pmatrix} \begin{pmatrix} {e^{t}}&{-e^{t}}\\ {e^{3t}}&{e^{3t}} \end{pmatrix}$

$$= \begin{pmatrix} \frac{1}{2}{e^{t}+e^{3t}}&{-e^{t}+e^{3t}}\\ {-e^{t}+e^{3t}}&{e^{t}+e^{3t}} \end{pmatrix} \label{5.19}$$

Ми бачимо, що походження також нестабільне в вихідних$x_{1}-x_{2}$ координатах. Його відносять до джерела, і це характеризується тим, що всі власні значення А мають позитивну дійсну частину. Фазовий портрет проілюстрований на рис.5.1.

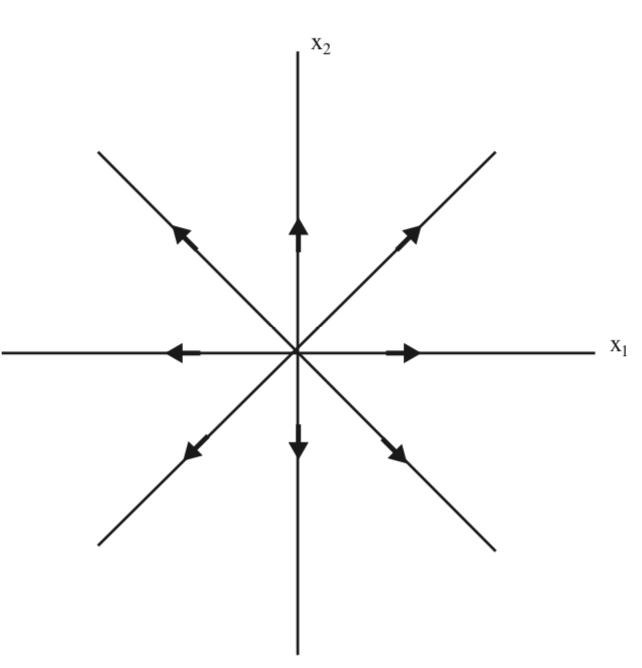
Зауважимо це можна зробити висновок про поведінку$e^{At}$ як$t \rightarrow \infty$ з поведінки,$e^{\Lambda t}$$t \rightarrow \infty$ оскільки Т не залежить від t.

Приклад$\PageIndex{11}$

Розглянемо наступні лінійні, автономні ОДУ:

$$\begin{pmatrix} {\dot{x_{1}}}\\ {\dot{x_{2}}} \end{pmatrix} = \begin{pmatrix} {-1}&{-1}\\ {9}&{-1} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} \label{5.20}$$

де

$$A = \begin{pmatrix} {-1}&{-1}\\ {9}&{-1} \end{pmatrix}, \label{5.21}$$

Крок 1. Обчислити власні значення A.

Власні значення А, що позначаються$\lambda$, задаються розв'язками характеристичного многочлена:

$det \begin{pmatrix} {-1-\lambda}&{-1}\\ {9}&{-1-\lambda} \end{pmatrix} = (-1-\lambda)^2+9 = 0$,

$$= \lambda^{2}+2\lambda+10 = 0, \label{5.22}$$

або

$\lambda_{1,2} = -1 \pm \frac{1}{2}\sqrt{4-40} = -1 \pm 3i$

Власні вектори є складними, тому ми знаємо, що він не діагональний над дійсними числами. Це означає, що ми не можемо знайти реальні власні вектори, щоб він міг бути перетворений у форму, де є дійсні числа на діагоналі та нулі у записах поза діагоналлю. Найкраще, що ми можемо зробити, це перетворити його у форму, де реальні частини власне значення знаходяться на діагоналі, а уявні частини знаходяться на вимкненому діагональному розташуванні, але вимкнені діагональні елементи відрізняються знаком мінус.

Крок 2. Обчислити власні вектори A.

Власний вектор A, відповідний власному вектору,$-1-3i$ є розв'язком наступних рівнянь:

$$\begin{pmatrix} {-1}&{-1}\\ {9}&{-1} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} = (-1-3i) \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.23}$$

або

$$-x_{1}-x_{2} = -x_{1}-3ix_{2}, \label{5.24}$$

$$9x_{1}-x_{2} = -x_{2}-3ix_{2}. \label{5.25}$$

Розв'язок цих рівнянь дається:

$\begin{pmatrix} {1}\\ {3i} \end{pmatrix} = \begin{pmatrix} {1}\\ {0} \end{pmatrix}+i \begin{pmatrix} {0}\\ {3} \end{pmatrix}$

Крок 3. Використовуйте власні вектори A для формування матриці перетворення T.

Для першого стовпця T візьмемо дійсну частину свого вектора, відповідну власному значенню$-1-3i$, а для другого - комплексну частину свого вектора:

$$T = \begin{pmatrix} {1}&{0}\\ {0}&{3} \end{pmatrix} \label{5.26}$$

з оберненою заданою:

$$T^{-1} = \begin{pmatrix} {1}&{0}\\ {0}&{\frac{1}{3}} \end{pmatrix} \label{5.27}$$

Крок 4. Обчислити$\Lambda = T^{-1}AT$.

$T^{-1}AT = \frac{1}{2}\begin{pmatrix} {1}&{0}\\ {0}&{\frac{1}{3}} \end{pmatrix} \begin{pmatrix} {-1}&{-1}\\ {9}&{-1} \end{pmatrix} \begin{pmatrix} {1}&{0}\\ {0}&{3} \end{pmatrix}$

$= \begin{pmatrix} {1}&{0}\\ {0}&{\frac{1}{3}} \end{pmatrix} \begin{pmatrix} {-1}&{-3}\\ {9}&{-3} \end{pmatrix}$

$$= \begin{pmatrix} {-1}&{-3}\\ {3}&{-1} \end{pmatrix} \equiv \Lambda \label{5.28}$$

$\Lambda$У цій формі ми знаємо з попереднього розділу, що:

$$e^{\Lambda t} = e^{-t}\begin{pmatrix} {cos3t}&{-sin3t}\\ {sin3t}&{cos3t} \end{pmatrix} \label{5.29}$$

Тоді у нас є:

$e^{At} = Te^{\Lambda t}T^{-1}$.

З цього виразу можна зробити висновок, що$e^{At} \rightarrow 0$ як$t \rightarrow \infty$. Звідси походження асимптотично стабільне. Його називають раковиною, і вона характеризується реальними частинами власних значень А, що є негативними. Фазова площина начерчена на рис.5.2.

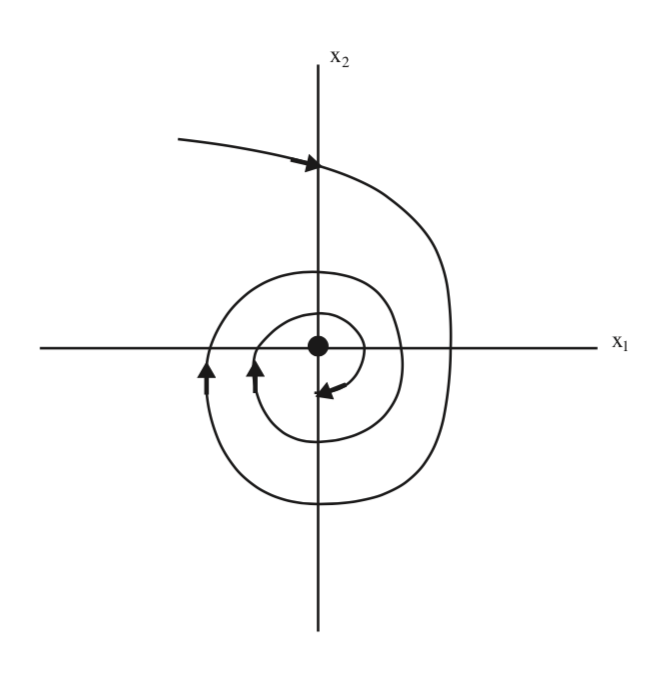
Приклад$\PageIndex{12}$

Розглянемо наступні лінійні, автономні ОДУ:

$$\begin{pmatrix} {\dot{x_{1}}}\\ {\dot{x_{2}}} \end{pmatrix} = \begin{pmatrix} {-1}&{1}\\ {1}&{1} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} \label{5.30}$$

де

$$A = \begin{pmatrix} {-1}&{1}\\ {1}&{1} \end{pmatrix}, \label{5.31}$$

Крок 1. Обчислити власні значення A.

Власні значення А, що позначаються$\lambda$, задаються розв'язками характеристичного многочлена:

$det \begin{pmatrix} {-1-\lambda}&{1}\\ {1}&{1-\lambda} \end{pmatrix} = (-1-\lambda)(1-\lambda)-1 = 0$

$$= \lambda^{2}-2 = 0, \label{5.32}$$

які є

$\lambda_{1,2} = \pm\sqrt{2}$

Крок 2. Обчислити власні вектори A.

Власний вектор, відповідний власному значенню,$\sqrt{2}$ задається розв'язком наступних рівнянь:

$$\begin{pmatrix} {-1}&{1}\\ {1}&{1} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} = \sqrt{2}\begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.33}$$

або

$$-x_{1}+x_{2} = \sqrt{2}x_{1}, \label{5.34}$$

$$x_{1}+x_{2} = \sqrt{2}x_{2}. \label{5.35}$$

Рішення дається:

$x_{2} = (1+\sqrt{2})x_{1}$.

що відповідає власному вектору

$\begin{pmatrix} {1}\\ {1+\sqrt{2}} \end{pmatrix}$

Власний вектор, відповідний власному значенню,$-\sqrt{2}$ задається розв'язком наступних рівнянь:

$$\begin{pmatrix} {-1}&{1}\\ {1}&{1} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} = -\sqrt{2}\begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.36}$$

або

$$-x_{1}+x_{2} = -\sqrt{2}x_{1}, \label{5.37}$$

$$x_{1}+x_{2} = -\sqrt{2}x_{2}. \label{5.38}$$

Рішення дається:

$x_{2} = (1-\sqrt{2})x_{1}$.

що відповідає власному вектору:

$\begin{pmatrix} {1}\\ {1-\sqrt{2}} \end{pmatrix}$

Крок 3. Використовуйте власні вектори A для формування матриці перетворення T.

Для стовпців T візьмемо власні вектори, відповідні власним значенням$\sqrt{2}$ і$-\sqrt{2}$:

$$T = \begin{pmatrix} {1}&{1}\\ {1+\sqrt{2}}&{1-\sqrt{2}} \end{pmatrix} \label{5.39}$$

з оберненою заданою:

$$T^{-1} = -\frac{1}{2\sqrt{2}}\begin{pmatrix} {1-\sqrt{2}}&{-1}\\ {-1-\sqrt{2}}&{1} \end{pmatrix} \label{5.40}$$

Крок 4. Обчислити$\Lambda = T^{-1}AT$. У нас є:

$T^{-1}AT = -\frac{1}{2\sqrt{2}}\begin{pmatrix} {1-\sqrt{2}}&{-1}\\ {-1-\sqrt{2}}&{1} \end{pmatrix} \begin{pmatrix} {-1}&{1}\\ {1}&{1} \end{pmatrix} \begin{pmatrix} {1}&{1}\\ {1+\sqrt{2}}&{1-\sqrt{2}} \end{pmatrix}$

$= -\frac{1}{2\sqrt{2}}\begin{pmatrix} {1-\sqrt{2}}&{-1}\\ {-1-\sqrt{2}}&{1} \end{pmatrix} \begin{pmatrix} {\sqrt{2}}&{-\sqrt{2}}\\ {2+\sqrt{2}}&{2-\sqrt{2}} \end{pmatrix}$

$$= \begin{pmatrix} {\sqrt{2}}&{0}\\ {0}&{-\sqrt{2}} \end{pmatrix} \equiv \Lambda \label{5.41}$$

Тому в$u_{1}-u_{2}$ координатах (5.30) стає:

$$\begin{pmatrix} {\dot{u_{1}}}\\ {\dot{u_{2}}} \end{pmatrix} = \begin{pmatrix} {\sqrt{2}}&{0}\\ {0}&{-\sqrt{2}} \end{pmatrix} \begin{pmatrix} {u_{1}}\\ {u_{2}} \end{pmatrix} \label{5.42}$$

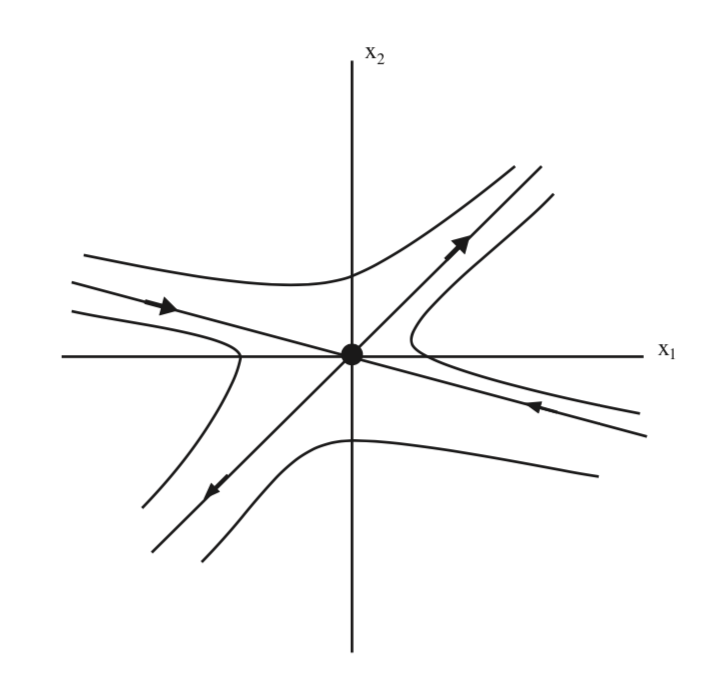
Фазовий портрет (5.42) показаний в 5.3.

Легко помітити, що походження нестабільне для (5.42). На рис. 5.3 ми бачимо, що походження має структуру сідлової точки, і ми хочемо вивчити цю ідею далі.

У$u_{1}-u_{2}$ координатах проліт власноговектора, відповідного власному значенню,$\sqrt{2}$ задається$u_{2} = 0$, тобто$u_{1}$ віссю. Проліт власного вектора, відповідного власному значенню,$-\sqrt{2}$ задається$u_{1} = 0$, тобто$u_{2}$ віссю. Більш того, ми бачимо з форми (5.42), що ці координатні осі є інваріантними. $u_{1}$Віссю називають нестабільним підпростором, позначається$E^{u}$, а$u_{2}$ вісь іменується як стійкий підпростір, позначається$E^{s}$. Іншими словами, нестабільний підпростір - це проміжок свого вектора, відповідного власному значенню з додатною дійсною частиною, а стабільний підпростір - проліт свого вектора, відповідного власному значенню, що має від'ємну дійсну частину. Стабільні та нестабільні підпростори є інваріантними підпросторами щодо потоку, породженого (5.42).

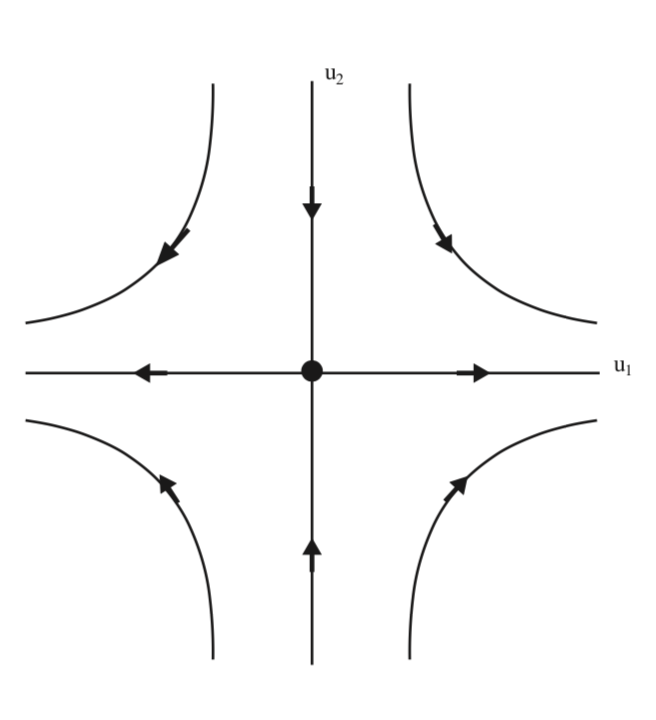
Стабільні та нестабільні підпростори відповідають осям координат у системі координат, заданих власними векторами. Далі ми хочемо зрозуміти, як вони будуть відображатися в вихідних$x_{1}-x_{2}$ координатах. Це досягається шляхом перетворення їх у вихідні координати за допомогою матриці перетворення (Equation\ ref {5.39}).

Спочатку ми трансформуємо нестабільний підпростір від$u_{1}-u_{2}$ координат до$x_{1}-x_{2}$ координат. У$u_{1}-u_{2}$ координатах точки на нестабільному підпросторі мають координати$(u_{1}, 0)$. Діючи на ці точки з Т дає:

$$T\begin{pmatrix} {u_{1}}\\ {0} \end{pmatrix} = \begin{pmatrix} {1}&{1}\\ {1+\sqrt{2}}&{1-\sqrt{2}} \end{pmatrix} \begin{pmatrix} {u_{1}}\\ {0} \end{pmatrix} = \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.43}$$

що дає наступне відношення між точками на нестабільному підпросторі в$u_{1}-u_{2}$ координатах до точок$x_{1}-x_{2}$ координат:

$$u_{1} = x_{1}, \label{5.44}$$

$$(1+\sqrt{2})u_{1} = x_{2}, \label{5.45}$$

або

$$(1 + \sqrt{2})x_{1} = x_{2}. \label{5.46}$$

Це рівняння для нестабільного підпростору в$x_{1}-x_{2}$ координатах, яке ми проілюструємо на рис.5.4.

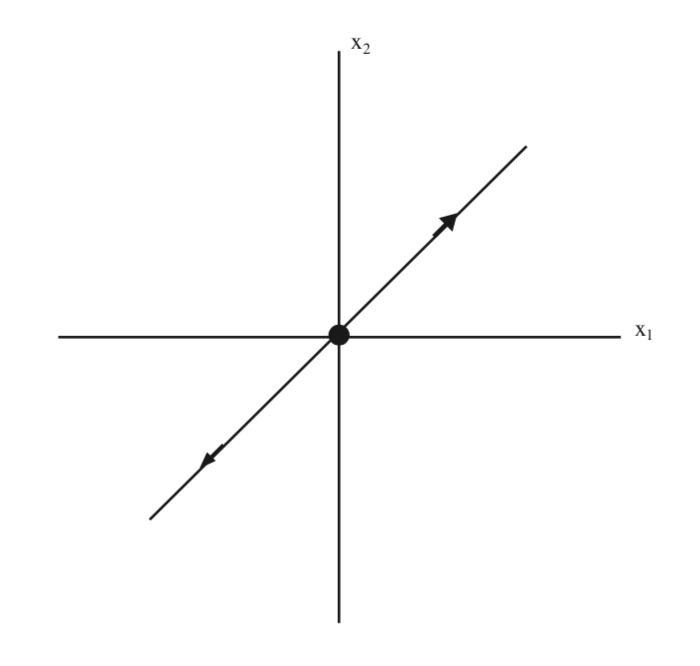
Далі ми трансформуємо стабільний підпростір від$u_{1}-u_{2}$ координат до$x_{1}-x_{2}$ координат. У$u_{1}-u_{2}$ координатах точки на стійкому підпросторі мають координати$(0, u_{2})$. Діючи на ці точки з Т дає:

$$T\begin{pmatrix} {0}\\ {u_{2}} \end{pmatrix} = \begin{pmatrix} {1}&{1}\\ {1+\sqrt{2}}&{1-\sqrt{2}} \end{pmatrix} \begin{pmatrix} {0}\\ {u_{2}} \end{pmatrix} = \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.47}$$

що дає наступне відношення між точками на стабільному підпросторі в$u_{1}-u_{2}$ координатах до точок$x_{1}-x_{2}$ координат:

$$u_{2} = x_{1}, \label{5.48}$$

$$(1-\sqrt{2})u_{2} = x_{2}, \label{5.49}$$

або

$$(1-\sqrt{2})x_{1} = x_{2}. \label{5.50}$$

Це рівняння для стійкого підпростору в$x_{1}-x_{2}$ координатах, яке ми проілюструємо на рис.5.5.

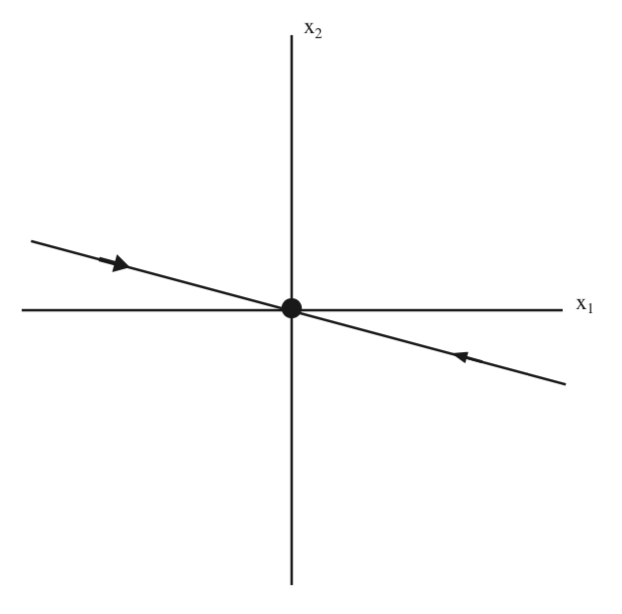
На рис. 5.6 ми проілюструємо як стабільний, так і нестабільний підпростори у вихідних координатах.