7.1: Регулярні багатокутники
- Page ID
- 58955
Правильний багатокутник - це багатокутник, в якому всі сторони рівні і всі кути рівні, Прикладами правильного багатокутника є рівносторонній трикутник (3 сторони), квадрат (4 сторони), правильний п'ятикутник (5 сторін) і правильний шестикутник (6 сторін). Кути правильного багатокутника легко знайти за допомогою методів розділу 1.5.
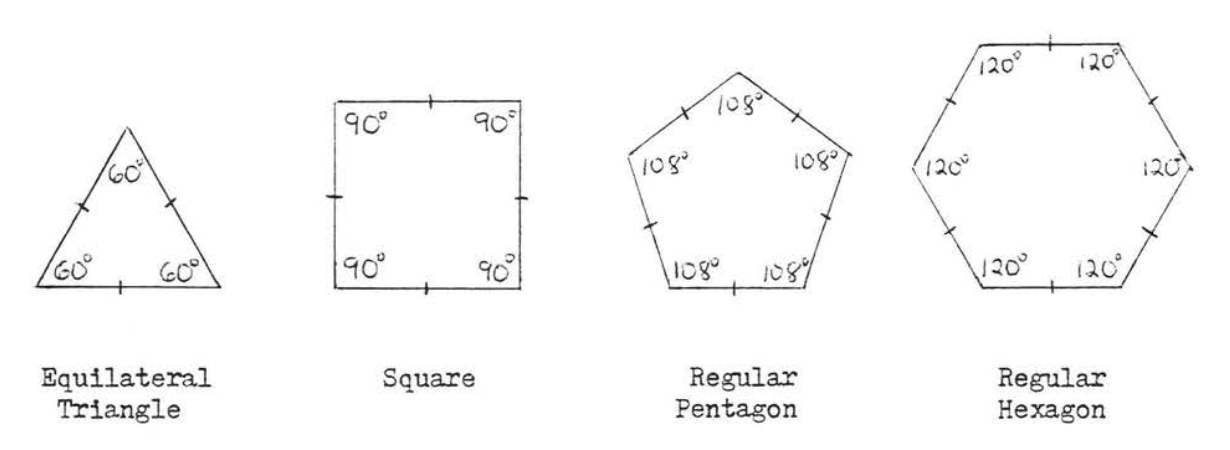
Припустимо, ми намалюємо бісектрису кута кожного кута правильного багатокутника, Ми знайдемо ці бісектриси кута всі зустрічаються в одній точці (рис.\(\PageIndex{2}\)).
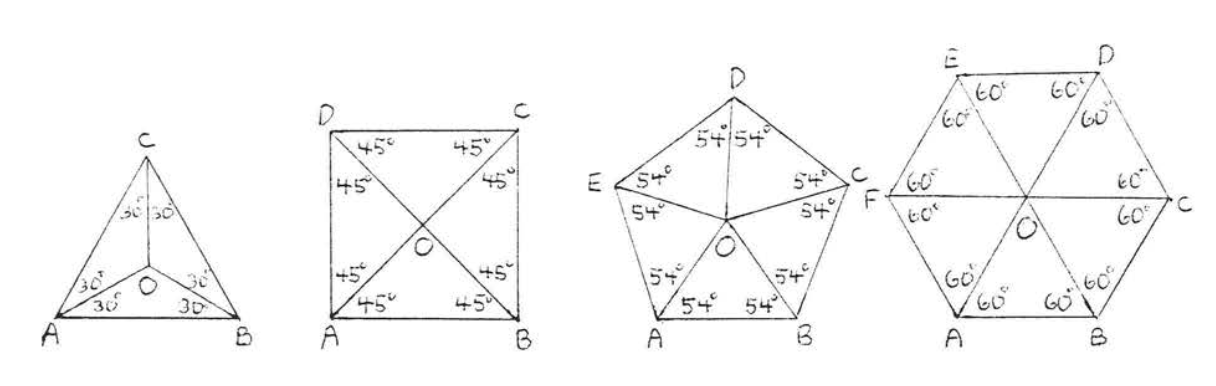
Бісектриси кута кожного кута правильного багатокутника зустрічаються в одній точці. Цю точку називають центром правильного багатокутника.
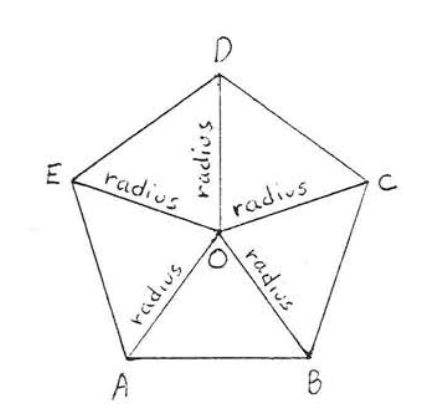
На рисунку\(\PageIndex{2}\). \(O\)центр кожного правильного багатокутника. Відрізок кожного бісектриси кута від центру до вершини називається радіусом. Наприклад\(OA, OB, OC, OD\), і\(OE\) являють собою п'ять радіусів правильного п'ятикутника\(ABCDE\).
Радіуси правильного багатокутника ділять багатокутник на конгруентні рівнобедрені трикутники. Всі радіуси рівні.
На малюнку\(\PageIndex{3}\) радіуси\(OA, OB, OC, OD\), а\(OE\) правильний п'ятикутник розділити на п'ять рівнобедрених трикутників с\(OA = OB =OC = OD = OE\).
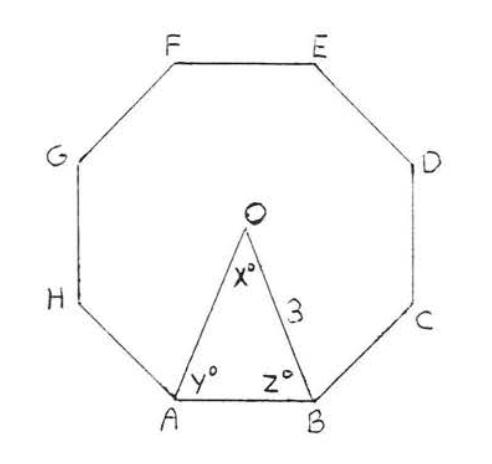
Знайдіть і радіус\(CA\), і кути\(x^{\circ}\)\(y^{\circ}\), і\(z^{\circ}\) в правильному восьмикутнику (восьмигранний малюнок):
Рішення
Радіуси ділять восьмикутник на 8 конгруентних рівнобедрених трикутників. Тому\(OA = OB = 3\).
\(x^{\circ} = \dfrac{1}{8} (360^{\circ}) = 45^{\circ}\).
\(y^{\circ}= z^{\circ} = \dfrac{1}{2}(180^{\circ} - 45^{\circ}) = \dfrac{1}{2} (135^{\circ}) = 67 \dfrac{1}{2}^{\circ}\).
Відповідь:\(OA = 3, x^{\circ} = 45^{\circ}, y^{\circ} = z^{\circ} = 67 \dfrac{1}{2}^{\circ}\).
Теорема\(\PageIndex{1}\) та теорема\(\PageIndex{2}\) здаються правдивими інтуїтивно, але ми перевіряємо їх формальним доказом:
Доказ теореми\(\PageIndex{1}\) та теореми\(\PageIndex{2}\): Доведемо ці теореми для правильного п'ятикутника. Доказ для інших правильних багатокутників аналогічний.
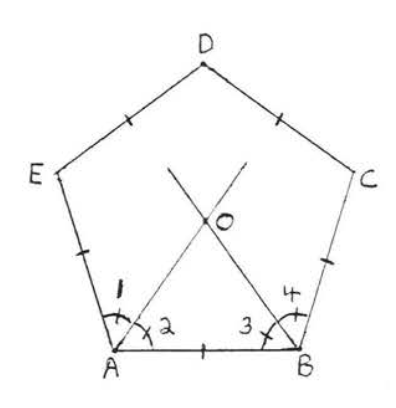
Намалюйте бісектриси кута\(\angle A\) і\(\angle B\) як показано на малюнку\(\PageIndex{4}\) and call their point of intersection \(O\). We will show \(OC, OD\), and \(OE\) are the angle bisectors of \(\angle C\), \(\angle D\), and \(\angle E\) respectively.
\(\angle EAB = \angle ABC\) since the angles of a regular pentagon are equal. \(\angle 1 = \angle 2 = \dfrac{1}{2}\) of \(\angle EAB = \dfrac{1}{2}\) of \(\angle ABC = \angle 3 = \angle 4\) since \(OA\) and \(OB\) are angle bisectors.
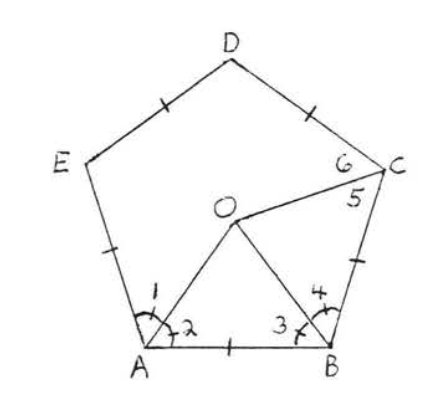
Малювати\(OC\) (Малюнок\(\PageIndex{5}\)). \(AB = BC\) since the sides of a regular pentagon are equal. Therefore \(\triangle AOB \cong \triangle COB\) by \(SAS = SAS\). Therefore \(\angle 5 = \angle 2 = \dfrac{1}{2}\) of \(\angle EAB = \dfrac{1}{2}\) of \(\angle BCD\). So \(OC\) is the angle bisector of \(\angle BCD\).
Аналогічно ми можемо показати бісектриси\(\triangle BOC \cong \triangle DOC\), \(\triangle COD \cong \triangle EOD\), \(\triangle DOE \cong \triangle AOE\) and that \(OD\) and \(OE\) are кута. Трикутники все рівнобедрені, тому що їх базові кути рівні. На цьому доказ завершено.
Відрізок лінії, проведений від центру перпендикулярно сторонам правильного багатокутника, називається апофемом (див. Рис.\(PageIndex{6}\)).
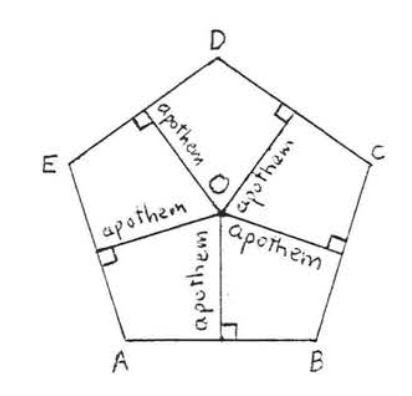
Апофеми правильного багатокутника всі рівні, Вони розділяють сторони правильного багатокутника.
- Доказ
-
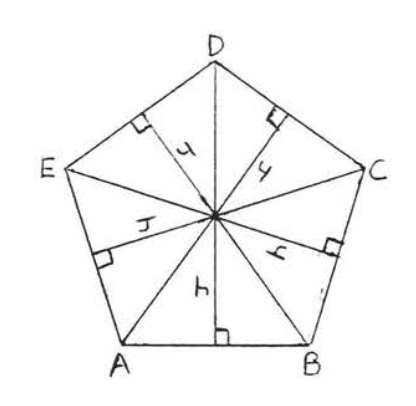
Всі апофеми рівні, оскільки вони є висотами конгруентних рівнобедрених трикутників, утворених радіусами (див. Теорема\(\PageIndex{2}\)), Кожен апофем ділить рівнобедрений трикутник на два конгруентні прямокутні трикутники, Тому кожен апофем бісектує сторону багатокутника, що ми хотіли довести.
Знайдіть апофем правильного п'ятикутника зі стороною 20, до найближчої десятої.
Рішення
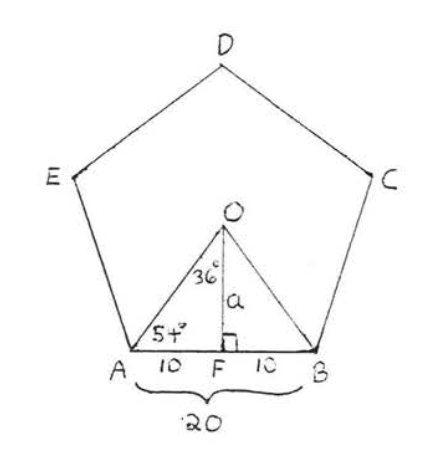
На\(\PageIndex{8}\) малюнку
\(\angle AOB = \dfrac{1}{5} (360^{\circ}) = 72^{\circ}\),
\(\angle AOF = \dfrac{1}{2}\angle AOB = \dfrac{1}{2} (72^{\circ}) = 36^{\circ}\),
і\(\angle OAF = 90^{\circ} - 36^{\circ} = 54^{\circ}\).
\(\begin{array} {rcl} {\tan 54^{\circ}} & = & {\dfrac{a}{10}} \\ {(10)1.3764} & = & {\dfrac{a}{10}(10)} \\ {13.764} & = & {a} \\ {13.8} & = & {a} \end{array}\)
Відповідь: 13.8
Апофем правильного багатокутника важливий, оскільки він використовується для пошуку площі:
Площа правильного багатокутника - половина добутку апотема і периметра.
\[A = \dfrac{1}{2} a P\]
- Доказ
-
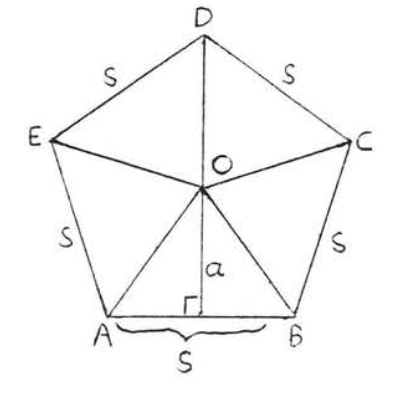
Малюнок\(PageIndex{9}\). Площа\(\triangle AOB\) є\(\dfrac{1}{2}\) як, де\(s\) знаходиться сторона п'ятикутника. Доведено теорему для правильного п'ятикутника. Доказ для інших правильних багатокутників аналогічний.
Радіуси правильного п'ятикутника ділять правильний п'ятикутник на п'ять конгруентних трикутників. Площа кожного трикутника дорівнює\(\dfrac{1}{2}\) як, де\(s\) сторона п'ятикутника (рис.\(PageIndex{9}\)). Отже, площа п'ятикутника = 5 (\ dfrac {1} {2} as) =\ dfrac {1} {2} a (5s) =\ dfrac {1} {2} aP\), що є формулою, яку ми хотіли довести.
Знайдіть площу правильного п'ятикутника зі стороною 20, до найближчої десятої.
Рішення
З прикладу,\(\PageIndex{2}\) який ми знаємо\(a = 13.764\). По периметру\(P = (5)(20) = 100\). Тому\(A = \dfrac{1}{2} aP = \dfrac{1}{2} (13.764)(100) = \dfrac{1}{2} (1376.4) = 688.2\).
Відповідь: 688.2
Щоб знайти периметр правильного багатокутника, все, що нам потрібно зробити, це помножити довжину сторони на кількість сторін. Наприклад, п'ятикутник фігури\(\PageIndex{8}\) має периметр\(P = 5(20)=100\). Однак також корисно мати формулу периметра, коли відомий лише радіус:
Периметр правильного багатокутника\(n\) сторін з радіусом\(r\) задається за формулою
\[P = 2 rn \sin \dfrac{180^{\circ}}{n}\]
- Доказ
-
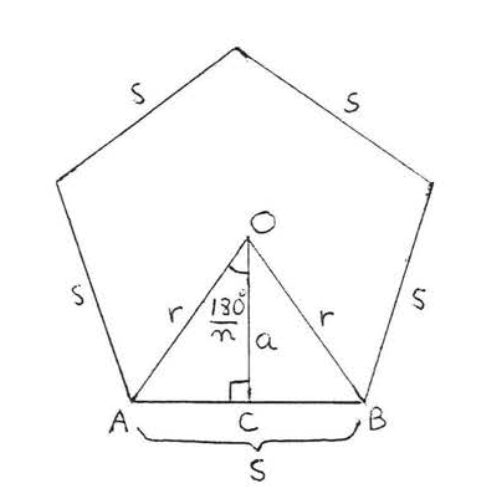
Малюнок\(\PageIndex{10}\): Правильний багатокутник з радіусом\(r\) і стороною\(s\). Давайте позначимо правильний багатокутник, як на малюнку\(PageIndex{10}\). Оскільки радіуси правильного багатокутника ділять багатокутник на\(n\) конгруентні трикутники (теорема\(\PageIndex{2}\)), ми маємо
\(\angle AOB = \dfrac{1}{n} (360^{\circ}) = \dfrac{360^{\circ}}{n}.\)
За теоремою\(\PageIndex{3}\) апофем\(OC\)\(AOB\) ділиться на два конгруентні прямокутні трикутники, так
\(\angle AOC = \dfrac{1}{2} \angle AOB = \dfrac{1}{2} (\dfrac{360^{\circ}}{n}) = \dfrac{180^{\circ}}{n}.\)
Застосовуючи тригонометрію до прямокутного трикутника,\(AOC\) ми маємо
\(\begin{array} {rcl} {\sin \dfrac{180^{\circ}}{n}} & = & {\dfrac{AC}{r}} \\ {(r)\sin \dfrac{180^{\circ}}{n}} & = & {\dfrac{AC}{r} (r)} \\ {r \sin \dfrac{180^{\circ}}{n}} & = & {AC} \end{array}\)
Так як\(OC\) бісекції\(AB\),
\(s = 2(AC)= 2r\sin \dfrac{180^{\circ}}{n}\)
і тому
\(P = ns = n(2r \sin \dfrac{180^{\circ}}{n}) = 2rn \sin \dfrac{180^{\circ}}{n}\)
яка є формулою, яку ми хочемо довести.
Знайдіть периметр правильного п'ятикутника радіусом 10, до найближчої десятої.
Рішення
П'ятикутник має\(n = 5\) бортики. Використовуючи формулу теореми\(\PageIndex{5}\),\(P = 2rn \sin \dfrac{180^{\circ}}{n} = 2(10)(5) \sin \dfrac{180^{\circ}}{5} = 100 \sin 36^{\circ} = 100(.5878) = 58.78 = 58.8.\)
Відповідь: 58.8.
Він також може дати явні формули для різних правильних багатокутників, як показано в наступній таблиці:
| Звичайна фігура | \(n\) | \(n \sin \dfrac{180^{\circ}}{n}\) | \(P = 2 rn \sin \dfrac{180^{\circ}}{n}\) |
|---|---|---|---|
| Трикутник | \ (n\) ">3 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(3 \sin 60^{\circ} = 2.5980\) | \ (P = 2 рн\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(5.1960\ r\) |
| Квадрат | \ (n\) ">4 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(4 \sin 45^{\circ} = 2.8284\) | \ (P = 2 рн\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(5.6568\ r\) |
| Пентагон | \ (n\) ">5 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(5 \sin 36^{\circ} = 2.9390\) | \ (P = 2 рн\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(5.8780\ r\) |
| Шестикутник | \ (n\) ">6 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(6 \sin 30^{\circ} = 3.0000\) | \ (P = 2 рн\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(6.0000\ r\) |
| Декагон | \ (n\) ">10 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(10 \sin 18^{\circ} = 3.090\) | \ (P = 2 рн\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(6.180\ r\) |
| 45-стороння фігура | \ (n\) ">45 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(45 \sin 4^{\circ} = 3.139\) | \ (P = 2 рн\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(6.278\ r\) |
| 90-стороння фігура | \ (n\) ">90 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(90 \sin 2^{\circ} = 3.141\) | \ (P = 2 рн\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(6.282\ r\) |
| 1000-стороння фігура | \ (n\) ">1000 | \ (n\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(1000 \sin 180^{\circ} = 3.1416\) | \ (P = 2 рн\ sin\ dfrac {180^ {\ circ}} {n}\) ">\(6.283\ r\) |
З таблиці\(\PageIndex{1}\) ми бачимо, що зі збільшенням кількості сторін периметр правильного багатокутника стає приблизно в 6,28 рази більше радіуса. Ви також можете визнати, що значення\(n \sin \dfrac{180^{\circ}}{n}\) наближається до числа\(\pi\). До цього моменту ми повернемося, коли обговоримо окружність кола в розділі 7.5.
Знайдіть периметр правильного п'ятикутника висотою радіусом 10, до найближчого десятого.
Рішення
Зі столу
\[ \begin{align*} P &= 5.8780\ r \\[4pt] &= 5.8780(10) \\[4pt] &= 58.78 \\[4pt] &= 58.8 \end{align*}.\]
Відповідь: 58.8.
Знайдіть апофем і площу правильного п'ятикутника радіусом 10, до найближчої десятої.
Рішення
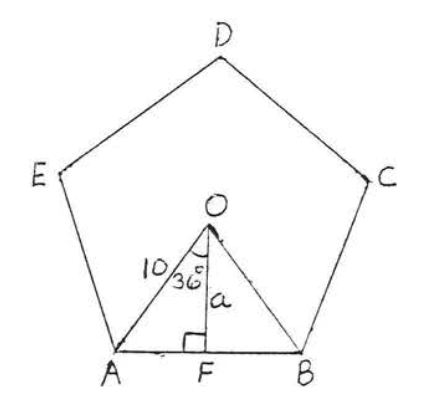
На малюнку\(\PageIndex{11}\)
\[\angle AOB = \dfrac{1}{5} (360^{\circ}) = 72^{\circ} \nonumber\]
і
\[\angle AOF = \dfrac{1}{2} \angle AOB = \dfrac{1}{2} (72^{\circ}) = 36^{\circ}. \nonumber\]
Застосовуючи тригонометрію до прямокутного трикутника\(AOF\),
\(\begin{array} {rcl} {\cos 36^{\circ}} & = & {\dfrac{a}{10}} \\ {(10).8090} & = & {\dfrac{a}{10}(10)} \\ {8.090} & = & {a} \end{array}\)
З прикладу\(\PageIndex{4}\),\(P = 58.78\). Тому, за теоремою\(\PageIndex{4}\),
\(A = \dfrac{1}{2} a P = \dfrac{1}{2} (8.09) (58.78) = \dfrac{1}{2} (475.5302) = 237.7651 = 237.8.\)
Відповідь:\(a = 8.1, P = 237.8\).
У 1936 році археологи розкопали групу стародавніх вавилонських таблиць, що містять формули для площ правильних багатокутників з трьох, чотирьох, п'яти, шести і семи сторін, Є докази того, що регулярні полігони були зазвичай використані в архітектурі і конструкції інших стародавніх цивілізацій, а також, класична Проблема грецької математики полягала в тому, щоб побудувати правильний багатокутник, використовуючи лише лінійку і компас, Регулярні багатокутники зазвичай вивчалися стосовно кіл. Як ми побачимо далі в цьому розділі, формули для площі та периметра кола можуть бути отримані з відповідних формул для правильних багатокутників.
Проблеми
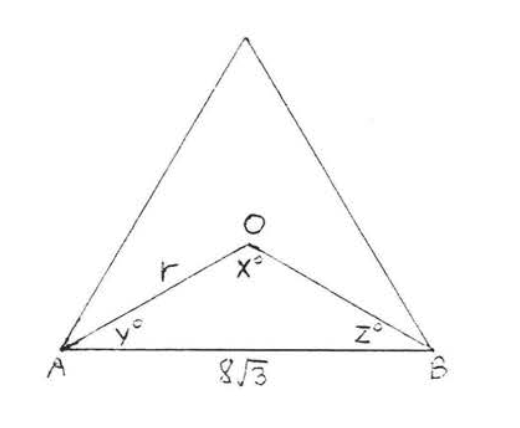
1 - 6. Знайдіть кути\(x^{\circ}, y^{\circ}, z^{\circ}\) і радіус\(r\) правильних багатокутників:
1.
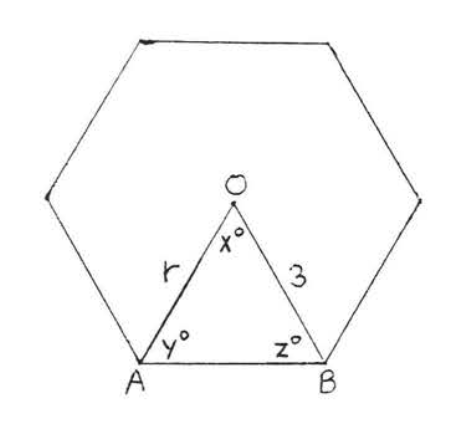
2.
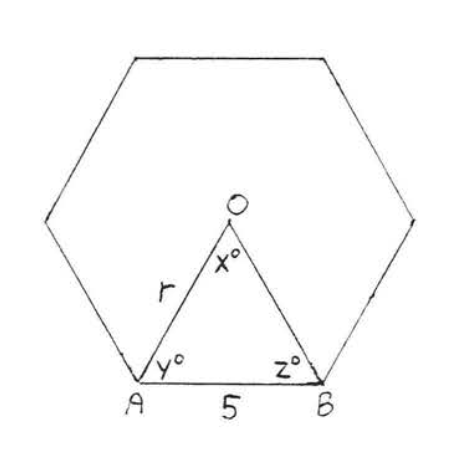
3.
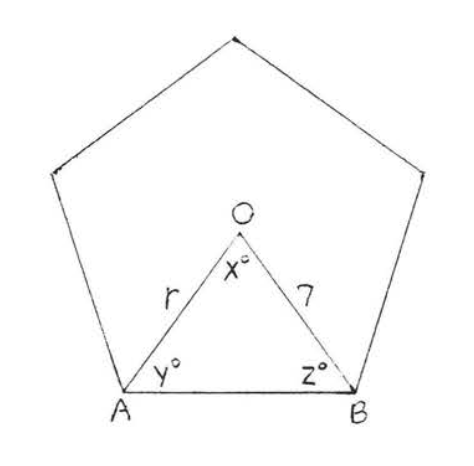
4.
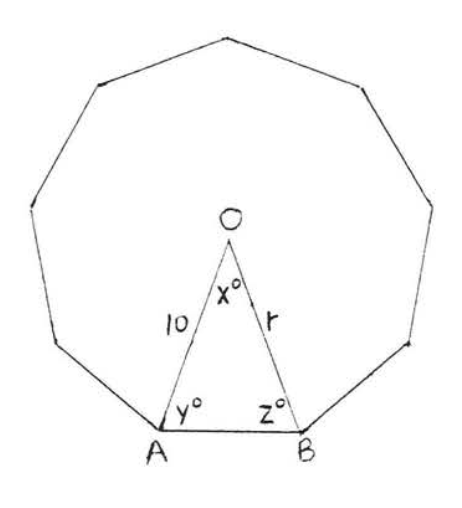
5.
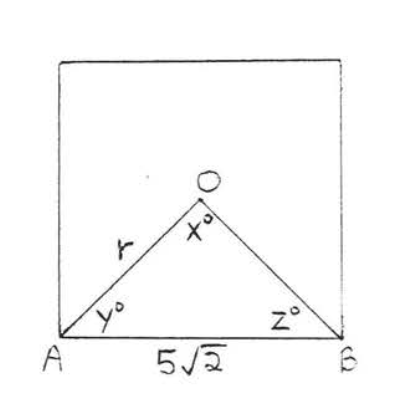
6.
7 - 18. Знайдіть апофем, периметр і площу до найближчої десятої:
7. звичайний п'ятикутник зі стороною 40.
8. звичайний п'ятикутник зі стороною 16.
9. звичайний шестикутник зі стороною 20.
10. звичайний шестикутник зі стороною 16.
11. звичайний декагон (десятистороння фігура) зі стороною 20.
12. звичайний нонагон (дев'ятистороння фігура) зі стороною 20.
13. звичайний п'ятикутник з радіусом 20.
14. звичайний п'ятикутник з радіусом 5.
15. звичайний шестикутник з радіусом 10.
16. правильний шестикутник з радіусом 20.
17. звичайний декагон з радіусом 10.
18. звичайний нонагон з радіусом 20.
