5.23: Побудувати регулярні багатокутники
- Page ID
- 54746
Побудувати креслення рівносторонніх трикутників, квадратів і правильних багатокутників за допомогою компаса і straightedge. Створіть багатокутники за допомогою Geogebra.
Конструкції правильних багатокутників
Використовуйте компас, щоб побудувати коло, як показано нижче на аркуші паперу. Опишіть, як скласти папір два рази, щоб допомогти вам побудувати квадрат.

Регулярні багатокутники
Правильний багатокутник - це багатокутник, який є рівнокутним і рівностороннім. Це означає, що всі його кути однакові, а всі його сторони мають однакову довжину.
Найосновнішим прикладом правильного багатокутника є рівносторонній трикутник, трикутник з трьома конгруентними сторонами і трьома конгруентними кутами. Квадрати - це також правильні багатокутники, тому що всі їх кути однакові (\(90^{\circ}\)), а всі їх сторони мають однакову довжину. Правильні багатокутники з п'ятьма і більше сторонами не мають спеціальних назв. Замість цього слово regular використовується для їх опису. Наприклад, правильний шестикутник - це шестикутник (6-сторонній багатокутник), кути якого всі однакові міри, а сторони все однакові довжини.
Всі правильні багатокутники мають симетрію обертання. Це означає, що обертання менше ніж\(360^{\circ}\) перенесе правильний багатокутник на себе. Насправді, правильний n-односторонній багатокутник має симетрію обертання для будь-якого кратного\(\dfrac{360^{\circ}}{n}\).
Конструкції - це покрокові процеси, що використовуються для створення точних геометричних фігур. Для створення конструкції своїми руками є кілька інструментів, які можна використовувати:
- Компас: Пристрій, що дозволяє створити коло із заданим радіусом. Компаси можуть не тільки допомогти вам створити кола, але також вони можуть допомогти вам копіювати відстані.
- Straightedge: Все, що дозволяє виробляти пряму лінію. Прямолінійний край не повинен вміти вимірювати відстані. Індексна картка добре працює як прямий край. Ви також можете використовувати лінійку як прямий край, якщо ви використовуєте її лише для малювання прямих ліній, а не для вимірювання.
- Папір: Коли геометрична фігура знаходиться на аркуші паперу, сам папір можна скласти, щоб побудувати нові лінії.
Ви можете побудувати деякі правильні багатокутники вручну, якщо пам'ятаєте визначення та властивості цих правильних багатокутників. За допомогою додаткового програмного забезпечення для геометрії або транспортира ви можете побудувати будь-який правильний багатокутник.
Давайте розглянемо приклад проблеми.
\(\overline{AB}\)це одна сторона того, що стане рівностороннім трикутником\(\Delta ABC\). Потрібно поставити крапку\(C\) в потрібному місці, щоб вийшов рівносторонній трикутник. Де повинна\(C\) бути розміщена точка щодо точок\(A\) і\(B\)?
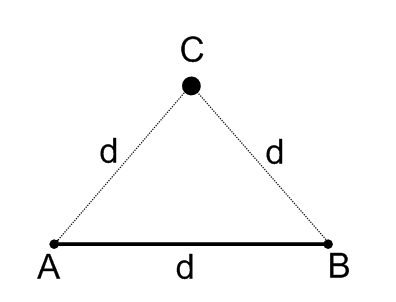
Нехай відстань між\(A\) і\(B\) буде\(d\). Точка\(C\) повинна бути d далеко від точки,\(A\) а також\(d\) далеко від точки\(B\).
Використовуйте прямий край, щоб намалювати відрізок лінії\(\overline{AB}\). Використовуйте ідеї з Прикладу А для побудови рівностороннього трикутника\(\Delta ABC\).
Використовуйте циркуль для вимірювання довжини\(\overline{AB}\).
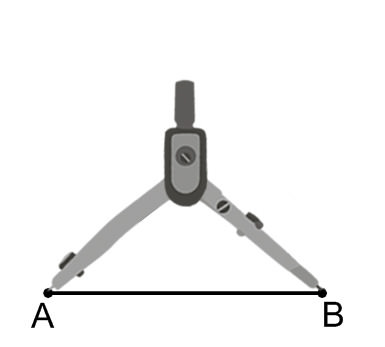
Зробіть часткове коло точок, які є довжиною\(\overline{AB}\) від точки\(A\).
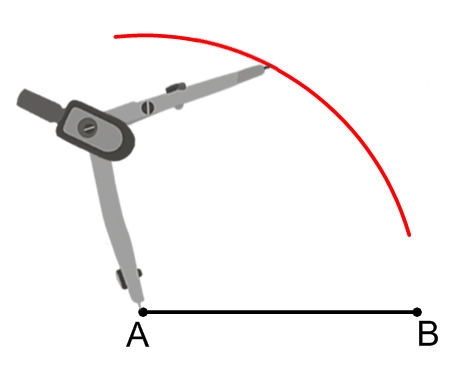
Зробіть ще одне часткове коло точок, які є довжиною\(\overline{AB}\) від точки\(B\).
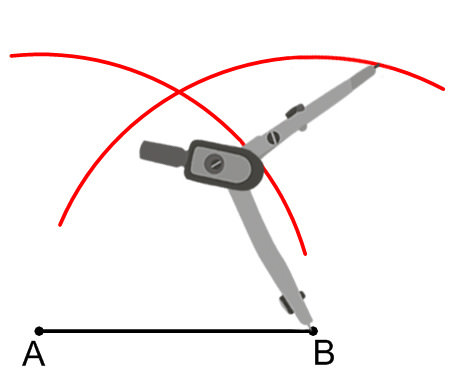
Точка перетину цих двох часткових кіл - точка\(C\).
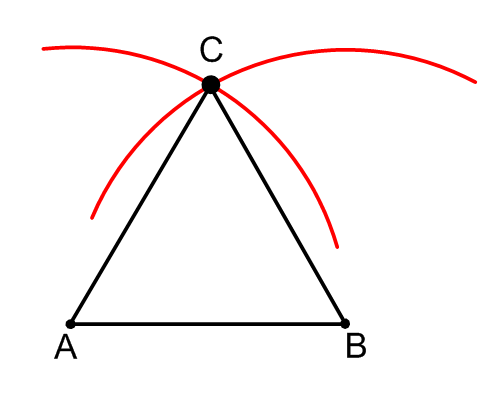
Точки\(A\)\(B\),\(C\),, і\(D\) знаходяться на колі з центром у точці\(O\). Доведіть, що\(ABCD\) це квадрат.
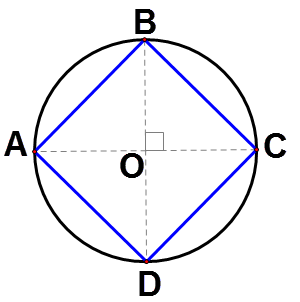
\(\overline{AO}\cong \overline{BO}\cong \overline{CO}\cong \overline{DO}\)тому що всі вони є радіусами одного кола. Так як\(\angle BOC\) це прямий кут\(\angle BOA\),\ кут AOD\) і\(\angle COD\) повинен бути також прямим кутом. Тому,\(\angle BOC\cong \angle BOA\cong \angle AOD\cong \angle COD\). Це означає, що\(\Delta BOC\cong \Delta AOB\cong \Delta DOA\cong \Delta COD\) за допомогою SAS\ cong\). \(\overline{AB}\cong \overline{BC}\cong \overline{CD}\cong \overline{DA}\)тому що вони є відповідними частинами конгруентних трикутників.
Всі чотири трикутники є рівнобедреними, оскільки кожен з них має дві конгруентні сторони. Це означає, що їх базові кути конгруентні. Оскільки кут вершини кожного трикутника є\(90^{\circ}\), базові кути кожного трикутника повинні бути\(45^{\circ} (90+45+45=180)\). Чотири кути, що складають чотирикутник, складаються з двох цих\(45^{\circ}\) кутів, і тому кожен\(90^{\circ}\).
Оскільки чотирикутник має чотири конгруентні сторони та чотири\(90^{\circ}\) кути, це квадрат.
Приклад\(\PageIndex{1}\)
Раніше вас попросили описати, як скласти папір два рази, щоб допомогти вам побудувати квадрат.
Рішення
Складіть коло так, щоб дві половинки перекривалися, щоб створити складку, яка є діаметром.
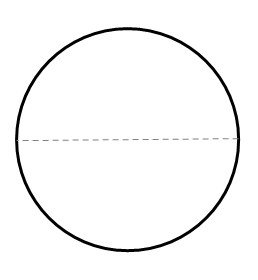
Знову складіть коло навпіл, щоб створити перпендикулярну бісектрису діаметра. Для цього складіть так, щоб зустрілися дві кінцеві точки діаметра. Друга складка теж буде діаметром.
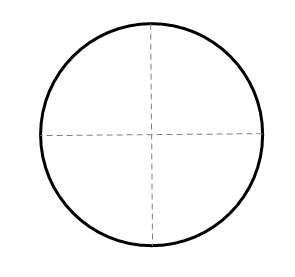
Зверніть увагу, що два діаметри перпендикулярні один одному. З'єднайте чотири точки перетину на колі, щоб побудувати квадрат.
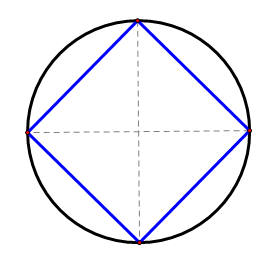
Ви можете бути впевнені, що це квадрат через доказ у прикладі C.
Приклад\(\PageIndex{2}\)
Правильний шестикутник нижче був розділений на шість конгруентних трикутників. Який тип трикутників вони бувають? Поясніть.
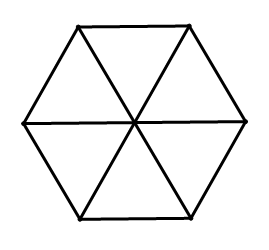
Рішення
Вони повинні бути рівносторонніми трикутниками.
- Повне коло є\(360^{\circ}\), тому кожен кут в центрі шестикутника повинен бути\(\dfrac{360^{\circ} }{6}=60^{\circ}\). * Ось чому регулярні шестикутники демонструють симетрію обертання в кратних\(60^{\circ}\) . *
- Шість трикутників є конгруентними, тому шість сегментів, що з'єднують центр шестикутника з вершинами, повинні бути конгруентними. Це означає, що шість трикутників є рівнобедреними.
- Базові кути кожного з рівнобедрених трикутників повинні бути\(\dfrac{180−60}{2}=60^{\circ}\).
- Міра кожного кута всіх трикутників є\(60^{\circ}\), тому всі трикутники рівносторонні.
Приклад\(\PageIndex{3}\)
Шість точок були рівномірно розташовані по колу нижче. Поясніть, чому створюється правильний шестикутник, коли ці точки з'єднані.
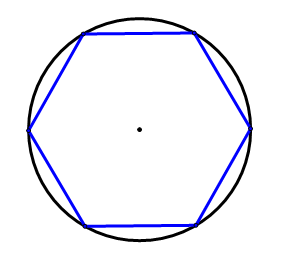
Рішення
Оскільки шість точок розташовані рівномірно, кожен з відрізків, що з'єднують шість точок, повинен бути однакової довжини. Тому багатокутник повинен бути правильним. Оскільки сторін шість, це повинен бути правильний шестикутник.
Приклад\(\PageIndex{4}\)
Побудуйте правильний шестикутник, вписаний в коло.
Рішення
«Вписані в коло» означає, що всі шість вершин шестикутника знаходяться на одному колі. Почніть з побудови кола і точки на колі.

Ви знаєте, що радіус кола такий же, як довжина кожної сторони кола (див. Керувану практику #1). Тому ваша мета полягає в тому, щоб розмістити шість точок навколо кола, які знаходяться на тій же відстані один від одного, що і радіус кола. Тримайте компас відкритим на ту ж ширину, що і радіус кола, і зробіть одну нову позначку на колі.
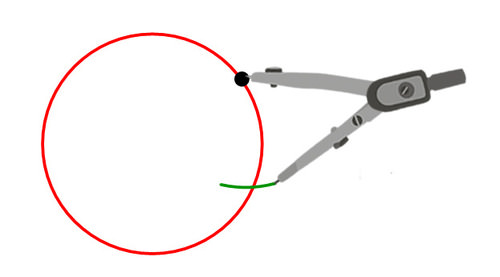
Продовжуйте робити нові позначки по колу, які знаходяться на однаковій відстані один від одного.

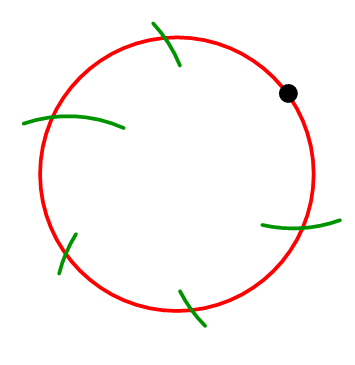
З'єднайте точки перетину, щоб сформувати правильний шестикутник.
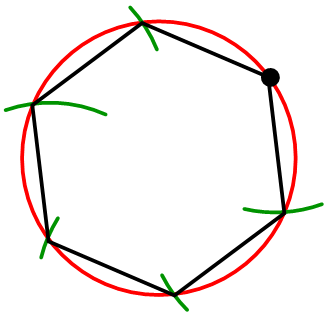
Рецензія
1. Побудувати рівносторонній трикутник.
2. Побудувати ще один рівносторонній трикутник.
3. Поясніть, чому працює ваш процес побудови рівносторонніх трикутників.
4. Побудуйте квадрат, вписаний в коло, зробивши дві складки.
5. Обґрунтуйте, чому багатокутник, який ви створили, насправді є квадратом.
Використовуйте свій straightedge для побудови\(\overline{AB}\).
6. Побудувати перпендикулярну бісектрису\(\overline{AB}\).
7. Побудуйте коло діаметром\(\overline{AB}\).
8. Побудуйте квадрат, вписаний в коло, з'єднавши чотири кінцеві точки діаметрів.
9. Розширте свою конструкцію до регулярного восьмикутника, розрізаючи кожен з прямих кутів у центрі кола.
10. Побудуйте правильний шестикутник, вписаний в коло.
11. Поясніть, чому метод побудови правильного шестикутника спирається на коло.
12. Поясніть, як ви могли б розширити свою конструкцію правильного шестикутника до конструкції регулярного 12-кутника.
13. Побудувати рівносторонній трикутник. Поясніть, як можна побудувати коло, яке проходить через три точки рівностороннього трикутника.
14. З огляду на рівносторонній трикутник, вписаний у коло, як можна розширити конструкцію, щоб побудувати правильний шестикутник?
15. З огляду на коло і транспортир, поясніть, як можна було створити звичайний п'ятикутник.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 5.4.
Лексика
| Термін | Визначення |
|---|---|
| Звичайний багатокутник | Правильний багатокутник - це багатокутник з усіма сторонами однакової довжини і всіма кутами однаковою мірою. |
| Рівносторонній | Багатокутник рівносторонній, якщо всі його сторони мають однакову довжину. |
| Рівнокутні | Багатокутник рівнокутний, якщо всі кути однакові. |