6.5: Площа трапеції
- Page ID
- 58880
На\(\PageIndex{1}\) малюнку\(b_1\) і\(b_2\) є підстави трапеції\(ABCD\) і\(h\) є висотою або висотою. Формула для площі наведена в наступній теоремі:
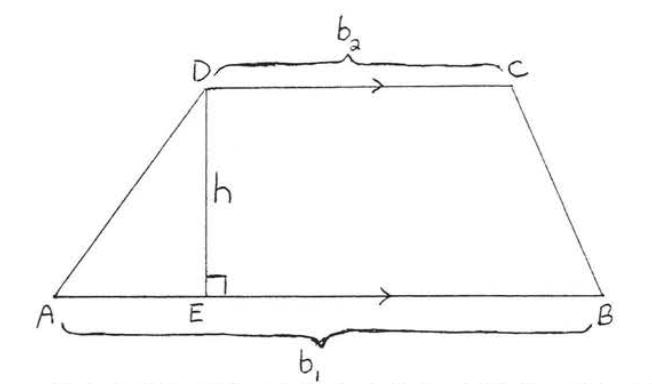
Площа трапеції дорівнює половині добутку її висоти і суми її підстав.
\[A = \dfrac{1}{2} h(b_1 + b_2)\]
- Доказ
-
На\(\PageIndex{1}\) малюнку малюємо\(BD\) (див. Малюнок\(\PageIndex{2}\)). Зверніть увагу, що\(CD = b_2\) є базою і\(BF = h\) є висотою\(\triangle BCD\). Площа трапеції\(ABCD =\) Площа\(\triangle ABD\) + Площа\(\triangle BCD\) =\(\dfrac{1}{2} b_1h + \dfrac{1}{2} b_2 h = \dfrac{1}{2} h(b_1 + b_2)\).
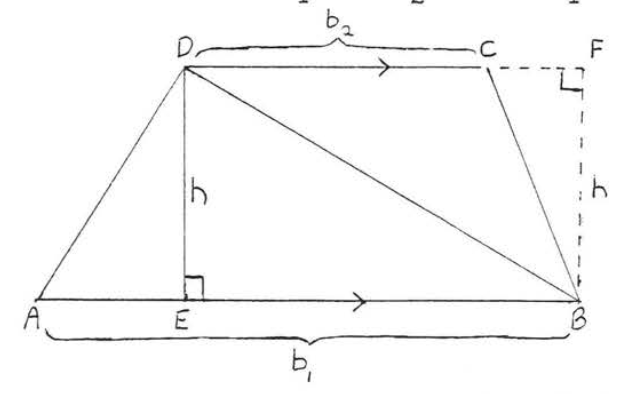
Малюнок\(\PageIndex{2}\): Малювати\(BD\). \(CD\)є підставою і\(BF\) є висотою\(\triangle BCD\).
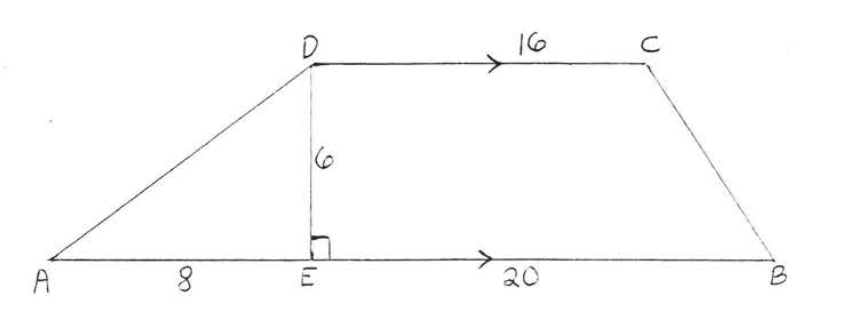
Знайдіть місцевість:
Рішення
\(A = \dfrac{1}{2} h(b_1 + b_2)= \dfrac{1}{2} (6)(28 + 16) = \dfrac{1}{2} (6)(44) = 132\).
Відповідь:\(A = 132\).
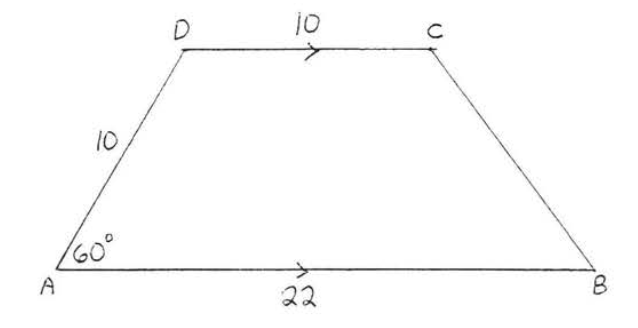
Знайдіть площу і периметр:
Рішення
Намалюйте висоти\(DE\) і\(CF\) (Малюнок\(\PageIndex{3}\)). \(\triangle ADE\)\(30^{\circ}-60^{\circ}-90^{\circ}\)трикутник. Так\(AE\) = короткий катет =\(\dfrac{1}{2}\) гіпотенуза =\(\dfrac{1}{2}(10) = 5\), а\(DE\) = довгий катет = (короткий катет) (\(\sqrt{3}\)) =\(5\sqrt{3}\). \(CDEF\)це прямокутник так\(EF = CD = 10\). Тому\(BF = AB - EF = 22 -10 - 5 = 7\). Нехай\(x = BC\).
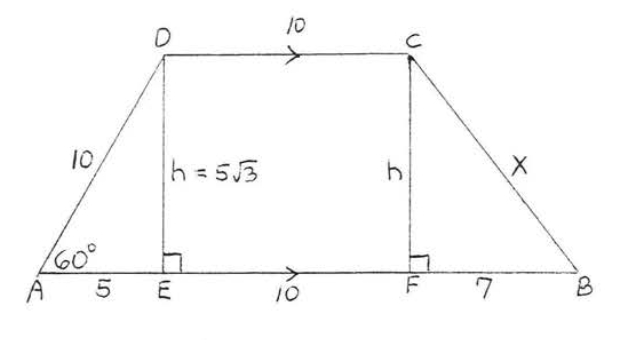
\[\begin{array} {rcl} {\text{CF}^2 + \text{BF}^2} & = & {\text{BC}^2} \\ {(5\sqrt{3})^2 + 7^2} & = & {x^2} \\ {75 + 49} & = & {x^2} \\ {124} & = & {x^2} \\ {x} & = & {\sqrt{124} = \sqrt{4} \sqrt{31} = 2\sqrt{31}} \end{array}\]
Площа =\(\dfrac{1}{2} h(b_1 + b_2) = \dfrac{1}{2} (5\sqrt{3}) (22 + 10) = \dfrac{1}{2} (5\sqrt{3})(32) = 80\sqrt{3}\).
Периметр =\(22 + 10 + 10 + 2\sqrt{31} = 42 + 2\sqrt{31}\).
Відповідь:\(A = 80\sqrt{3}\),\(P = 42 + 2\sqrt{31}\).
Проблеми
1 - 2. Знайдіть площу\(ABCD\):
1.
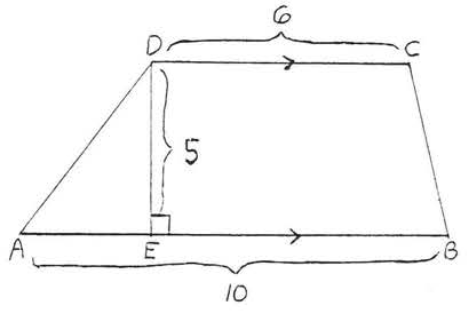
2.
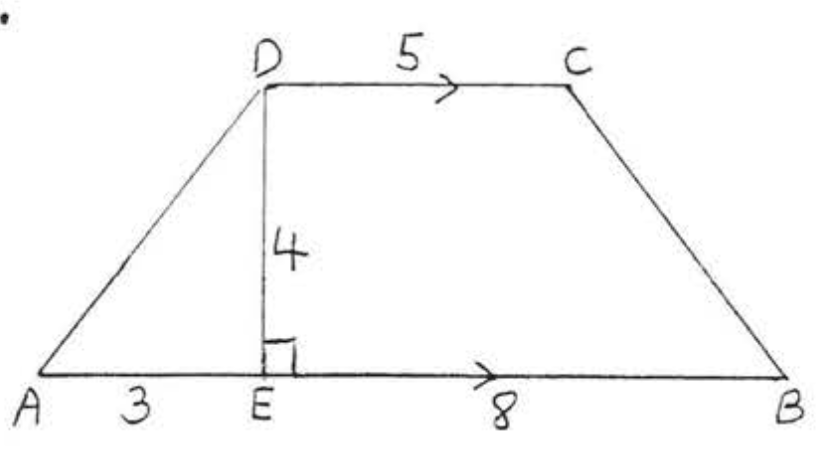
3 - 12. Знайдіть площу і периметр\(ABCD\):
3.
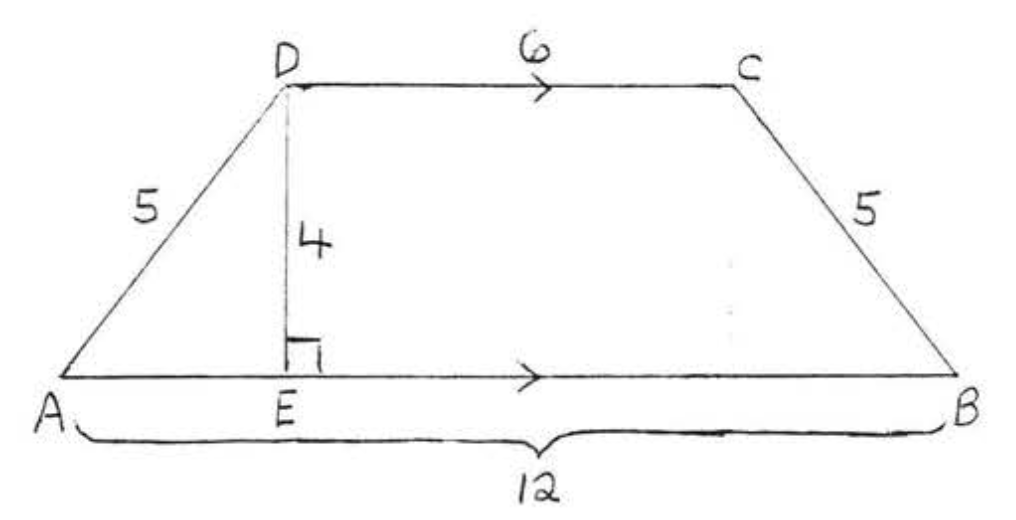
4.
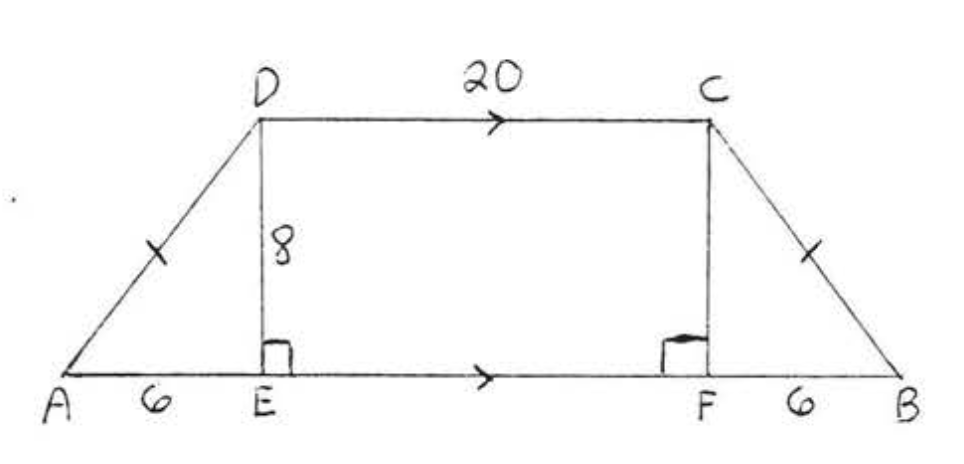
5.
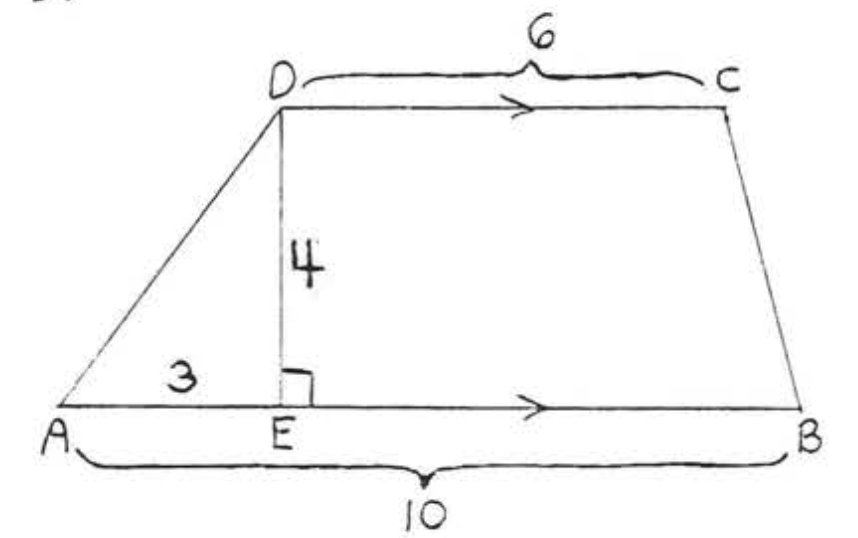
6.
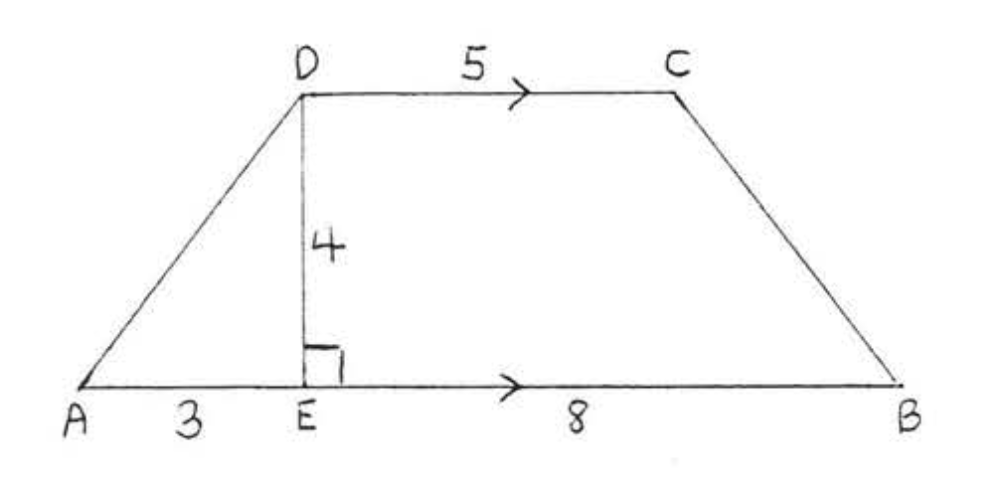
7.
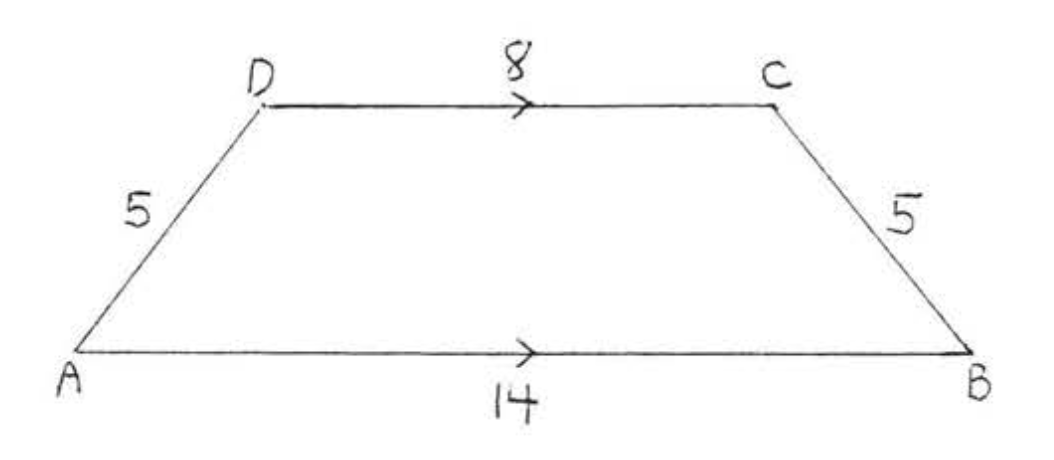
8.
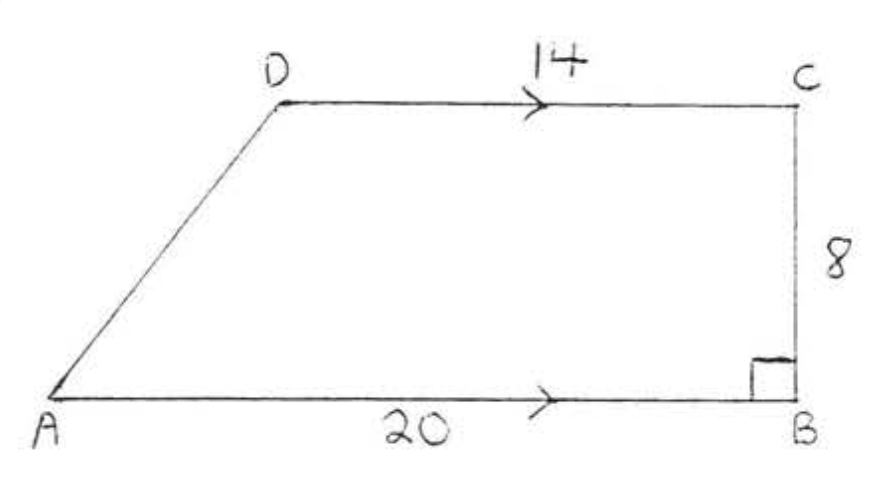
9.
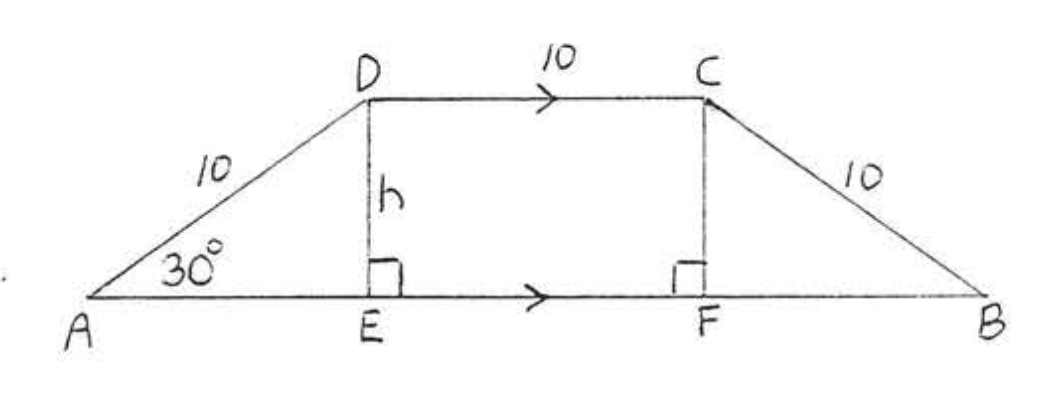
10.
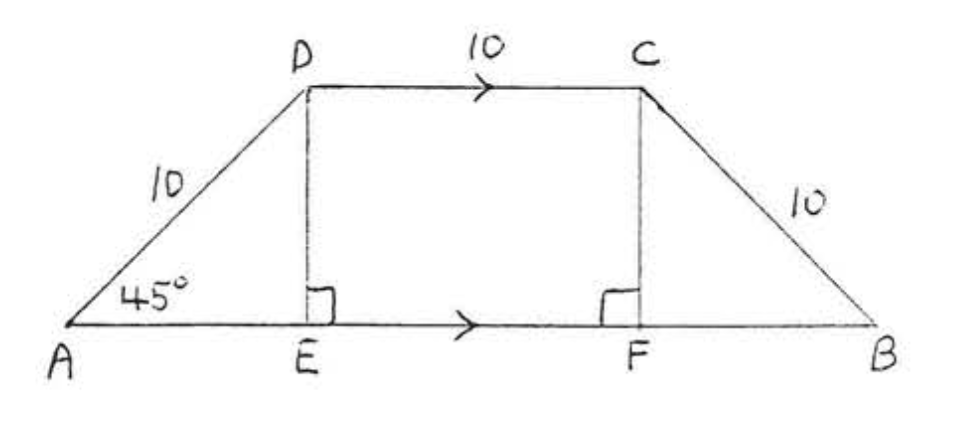
11.
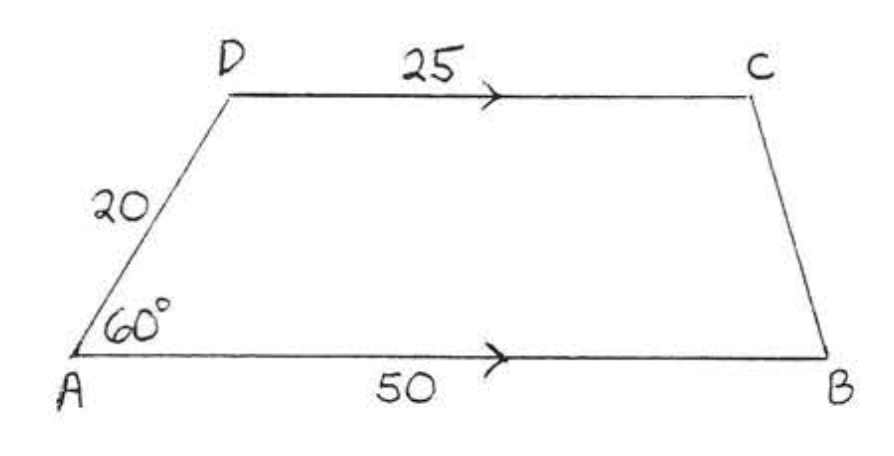
12.
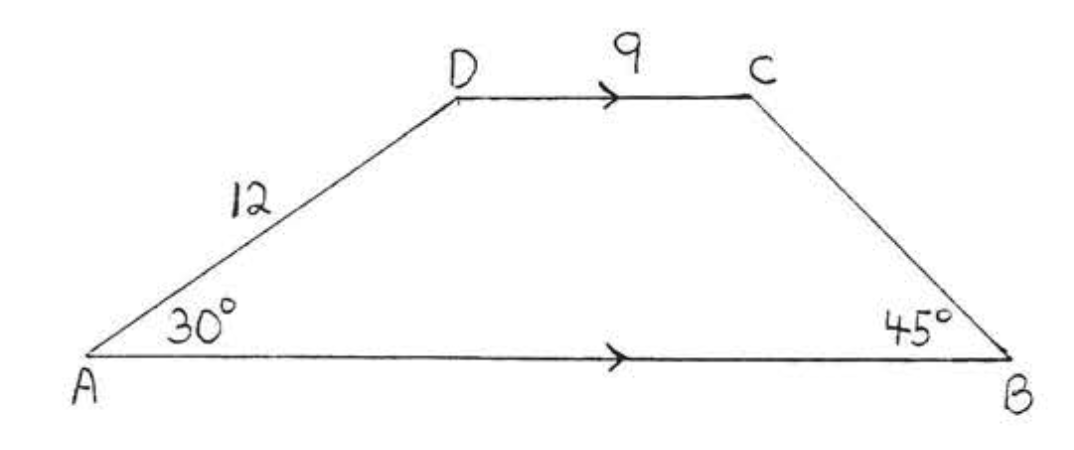
13 - 14. Знайдіть площу і периметр до найближчої десятої частини\(ABCD\):
13.
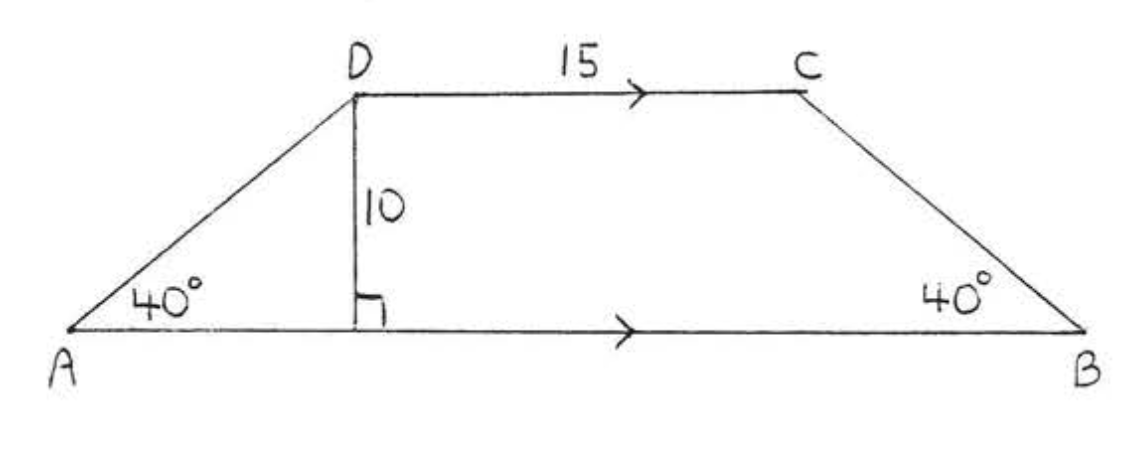
14.
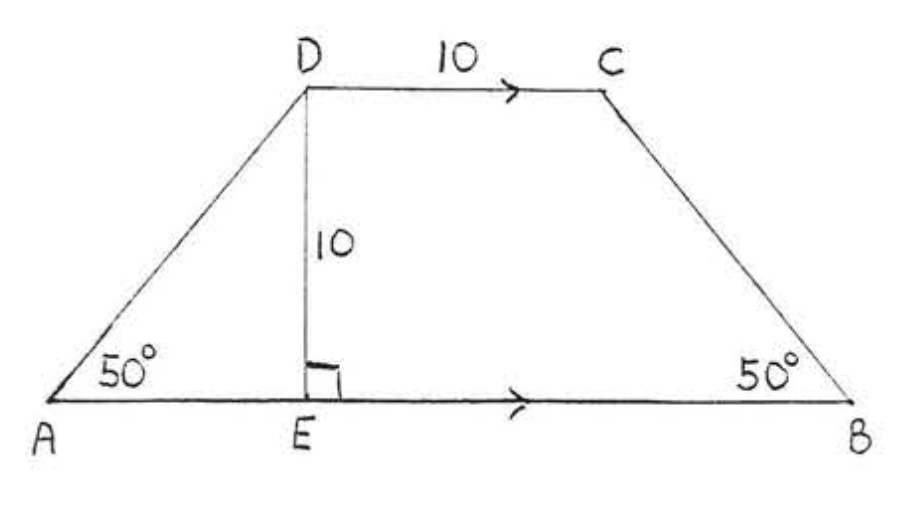
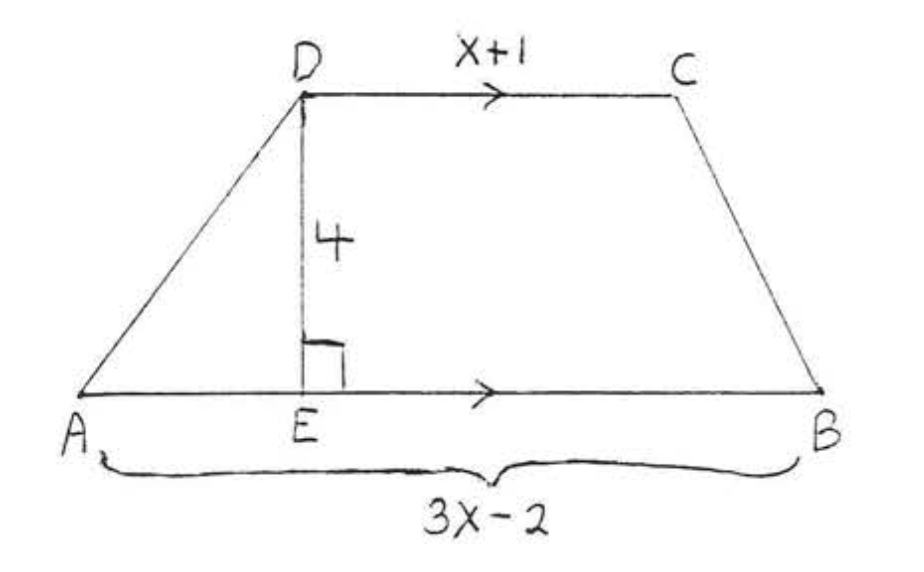
15. Знайти,\(x\) якщо площа\(ABCD\) дорівнює 50:
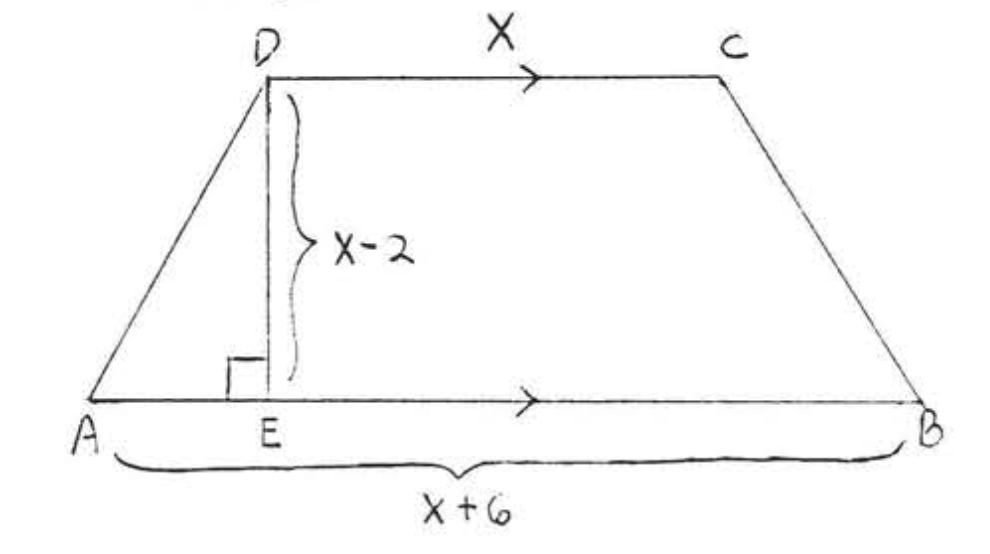
16. Знайти,\(x\) якщо площа 30:\(ABCD\)