3.2: Інші чотирикутники

У цьому розділі ми розглянемо інші чотирикутники зі спеціальними властивостями: ромб, прямокутник, квадрат і трапеція.

Малюнок$\PageIndex{1}$: Ромб.

Малюнок$\PageIndex{2}$: Ромб з діагоналями.

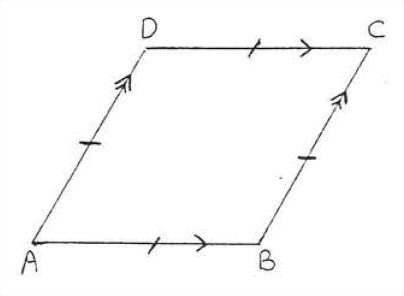
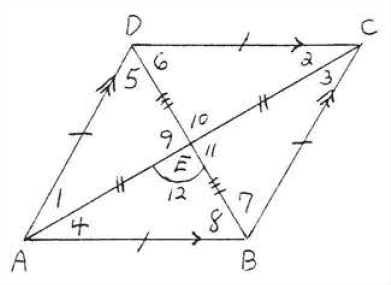
Ромб - це паралелограм, в якому всі сторони рівні (рис.$\PageIndex{1}$). Він має всі властивості паралелограма плюс деякі додаткові, а також. Намалюємо діагоналі$AC$ і$BD$ (рис.$\PageIndex{2}$). За теоремою$\PageIndex{3}$ розділу 3.1 діагоналі розділяють один одного. Звідси

$$\triangle ADE \cong \triangle CDE \cong \triangle CBE \cong \triangle ABE \nonumber$$

по$SSS = SSS$. Відповідні кути конгруентних трикутників рівні:

$$\angle 1 = \angle 2 = \angle 3 = \angle 4, \nonumber$$

$$\angle 5 = \angle 6 = \angle 7 = \angle 8 \nonumber$$

і

$$\angle 9 = \angle 10 = \angle 11 = \angle 12. \nonumber$$

$\angle 9$і$\angle 10$ є додатковими на додаток до рівних, отже$\angle 9 = \angle 10 = \angle 11 = \angle 12 = 90^{\circ}$. Ми довели наступну теорему:

Теорема$\PageIndex{1}$

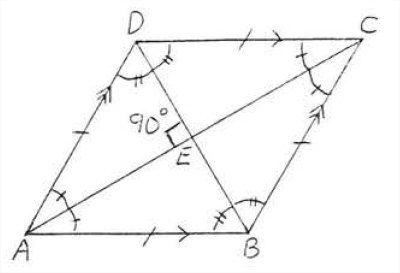
Діагоналі ромба перпендикулярні і бісекційні кути. Див$\PageIndex{3}$. Малюнок.

Малюнок$\PageIndex{3}$: Діагоналі ромба перпендикулярні і бісекційні кути.

Приклад$\PageIndex{1}$

Знайти$w$,$x$,$y$, і$z$:

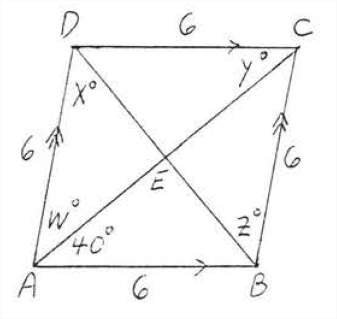
Рішення

$ABCD$є ромбом, оскільки це паралелограм, всі сторони якого дорівнюють 6. Згідно теоремі$\PageIndex{1}$, діагоналі перпендикулярні і бісекційні кути. Тому$w^{\circ}=40^{\circ}$ з$AC$ бісекцій$\angle BAD$. $\angle AED = 90^{\circ}$так$x^{\circ} = 180^{\circ} - (90^{\circ} + 40^{\circ}) = 180^{\circ} - 130^{\circ} = 50^{\circ}$ (сума кутів$\angle AED$ є$180^{\circ}$). Нарешті$y^{\circ} = w^{\circ} = 40^{\circ}$ (порівняйте з малюнком$\PageIndex{3}$) і$z^{\circ} = x^{\circ} = 50^{\circ}$.

Відповідь

$w = 40, x = 50, y = 40, z = 50$.

$\PageIndex{4}$На малюнку зображений ромб$ABCD$ Прикладу$\PageIndex{1}$ з усіма його кутами ідентифіковані.

Малюнок$\PageIndex{4}$: Ромб Прикладу$\PageIndex{1}$ з усіма кутами ідентифіковані.

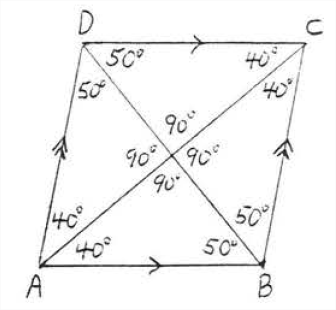
Прямокутник - це паралелограм, в якому всі кути є прямими кутами (рис.$\PageIndex{5}$). Він має всі властивості паралелограма плюс деякі додаткові, а також. Насправді не потрібно говорити, що всі кути є прямими кутами:

Малюнок$\PageIndex{5}$: Прямокутник.

Малюнок$\PageIndex{6}$: Паралелограм з одним прямим кутом також повинен бути прямокутником.

Теорема$\PageIndex{2}$

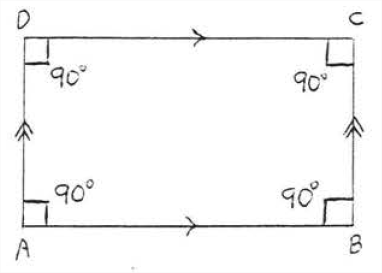
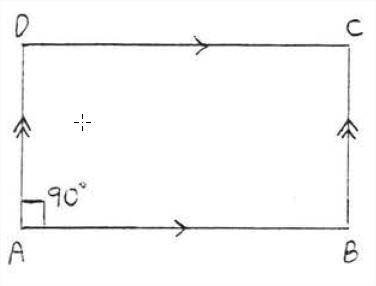
Паралелограм з одним прямим кутом повинен бути прямокутником.

На малюнку$\PageIndex{6}$$\angle A$ якщо прямий кут, то всі інші кути повинні бути прямими кутами теж.

Доказ

На малюнку$\PageIndex{6}$,$\angle C = \angle A = 90^{\circ}$ тому що протилежні кути паралелограма рівні (Теорема$\PageIndex{1}$, розділ 3.1). $\angle B = 90^{\circ}$і$\angle D = 90^{\circ}$ тому, що послідовні кути паралелограма є додатковими (Теорема$\PageIndex{2}$, розділ 3.2).

Приклад$\PageIndex{2}$

Знайти$x$ і$y$:

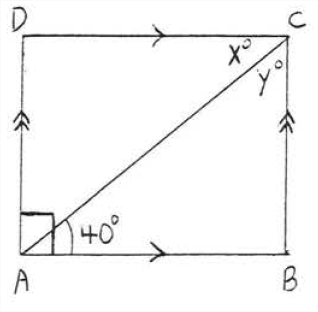
Рішення

Теорема$\PageIndex{2}$,$ABCD$ являє собою прямокутник. $x^{\circ}=40^{\circ}$тому що внутрішні кути чергуються паралельними лініями$AB$ і$CD$ повинні бути рівними. Так як фігура являє собою прямокутник$\angle BCD = 90^{\circ}$ і$y^{\circ} = 90^{\circ} - x^{\circ} = 90^{\circ} - 40^{\circ} = 50^{\circ}.$

Відповідь:$x = 40, y = 50$

Намалюємо діагоналі прямокутника$ABCD$ (рис.$\PageIndex{7}$).

Малюнок$\PageIndex{7}$: Прямокутник З намальованими діагоналями.

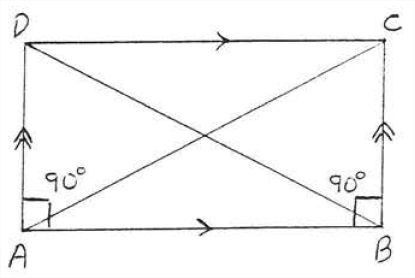
Ми покажемо$\triangle ABC \cong \triangle BAD$. $AB = BA$через ідентичність. $\angle A = \angle B = 90^{\circ}$. $BC = AD$тому що протилежні сторони паралелограма рівні. Потім$\triangle ABC \cong \triangle BAD$ мимо$SAS = SAS$. Тому$AC =$ діагональні діагоналі,$B D$ оскільки вони відповідають сторонам конгруентних трикутників. Ми довели:

Теорема$\PageIndex{3}$

Діагоналі прямокутника рівні. На малюнку$\PageIndex{7}$,$AC = BD$.

Приклад$\PageIndex{3}$

Знайти$w$,$x$,$y$,$z$,$AC$ і$BD$:

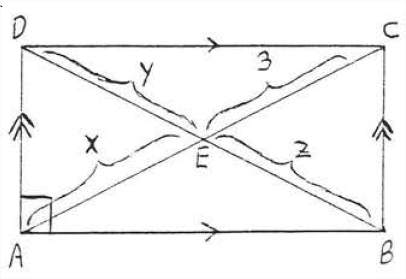
Рішення

$x = 3$тому що діагоналі паралелограма розсікають один одного. Отже$AC = 3 + 3 = 6$. $BD = AC = 6$так як діагоналі прямокутника рівні (теорема$\PageIndex{3}$). Тому$y = z = 3$ так як діагональ$BD$ розділена на діагональ$AC$.

Відповідь:$x= y = z = 3$ і$AC = BD = 6$.

Приклад$\PageIndex{4}$

Знайти$x$$y$, і$z$:

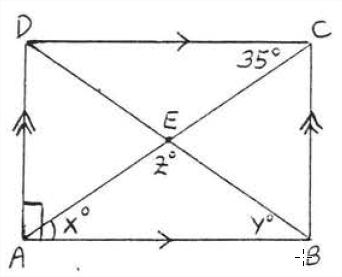
Рішення

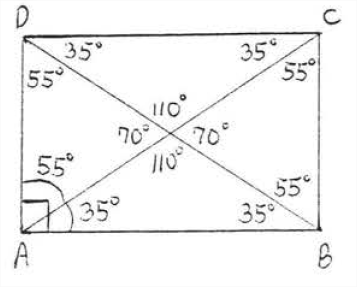
$x^{\circ} = 35^{\circ}$, Тому що поперемінні внутрішні кути паралельних ліній рівні. $y^{\circ} = x^{\circ} = 35^{\circ}$тому що вони є базовими кутами рівнобедреного трикутника$ABE$ так (AE= BE\), тому що діагоналі прямокутника рівні і бісекція один одного). $z^{\circ} = 180^{\circ} - (x^{\circ} + y^{\circ}) = 180^{\circ} - (35^{\circ} + 35^{\circ}) = 180^{\circ} - 70^{\circ} = 110^{\circ}$. $\PageIndex{8}$На малюнку зображений прямокутник$ABCD$ з усіма кутами ідентифіковані.

Відповідь:$x=y=z=3, A C=B D=6$.

Малюнок$\PageIndex{8}$: Прямокутник Прикладу$\PageIndex{4}$ з усіма визначеними кутами.

Площа

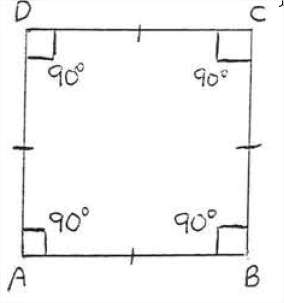
Квадрат - це прямокутник з усіма його сторонами рівними. Тому це також ромб. Так що він має всі властивості прямокутника і всі властивості ромба.

Малюнок$\PageIndex{9}$: Квадрат.

Малюнок$\PageIndex{10}$: Трапеція.

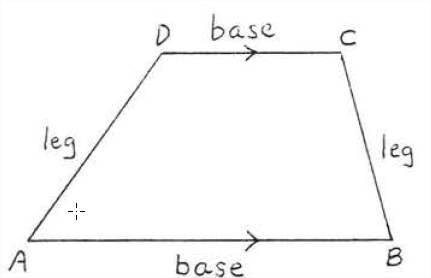
Трапеція - це чотирикутник з двома і тільки двома сторонами паралельними. Паралельні сторони називаються підставами, а дві інші сторони називаються ніжками. На малюнку$\PageIndex{8}$$AB$ і$CD$ є підстави$AD$ і і$BC$ є ноги. $\angle A$і$\angle B$ являють собою пару базових кутів. $\angle C$і$\angle D$ є ще однією парою базових кутів.

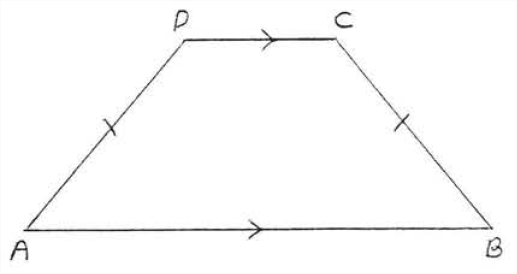
Рівнобедрений трапеція - це трапеція, в якій ноги рівні. На малюнку$\PageIndex{8}$,$ABCD$ являє собою рівнобедрену трапецію с$AD = BC$. Рівнобедрений трапеція має наступну властивість:

Теорема$\PageIndex{4}$

Базові кути рівнобедреної трапеції рівні. На малюнку$\PageIndex{11}$,$\angle A = \angle B$ і$\angle C = \angle D$

Малюнок$\PageIndex{11}$: Рівнобедрений трапеція

Приклад$\PageIndex{5}$

Знайти$x, y$, і$z:$

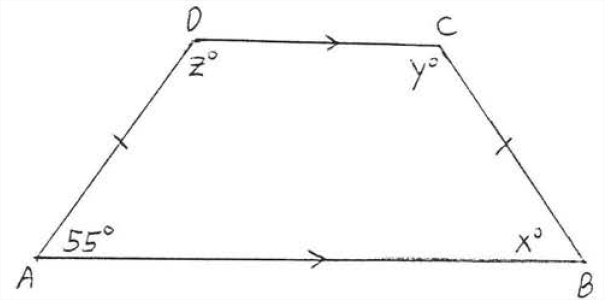
Рішення

$x^{\circ}=55^{\circ}$тому що$\angle A$ і$\angle B$, базові кути рівнобедреної трапеції$ABCD$, рівні. Тепер внутрішні кути паралельних ліній на тій же стороні поперечної є додатковими (Теорема 3 розділ 1.4). Тому$y^{\circ} = 180^{\circ} - x^{\circ} = 180^{\circ} - 55^{\circ} = 125^{\circ}$ і$z^{\circ} = 180^{\circ} - 55^{\circ} = 125^{\circ}$.

Відповідь:$x = 22$,$y = z = 125$.

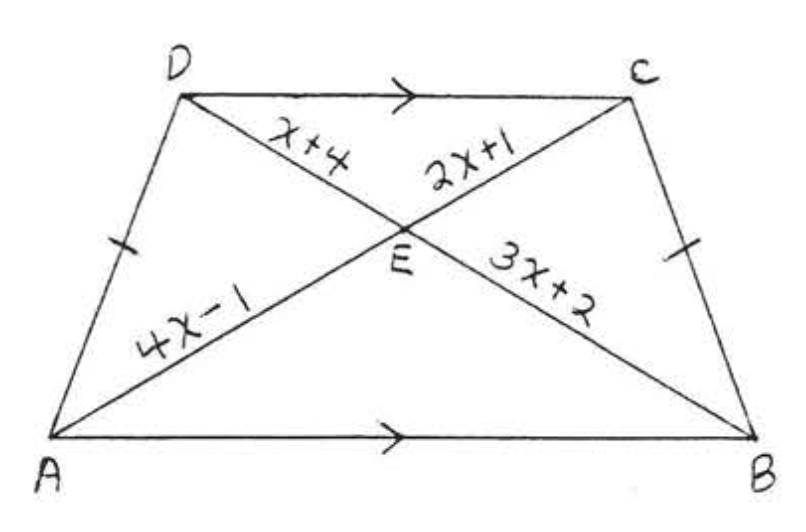
Доказ теореми$\PageIndex{4}$: Draw $DE$ parallel to $CB$ as in Figure $\PageIndex{12}$. $\angle 1 = \angle B$ because corresponding angles of parallel lines are equal, $DE = BC$ because they are the opposite sides of parallelogram $BCDE$. Therefore $AD = DE$. So $\triangle ADE$ is isosceles and its base angles, $\angle A$ and $\angle 1$, are equal. We have proven $A = \angle 1 = \angle B$. To prove $\angle C = \angle D$, observe that they are both supplements of $\angle A = \angle B$ (Theorem $\PageIndex{3}$, section 1.4).

Рівнобедрений трапеція має одну додаткову властивість:

Теорема$\PageIndex{5}$

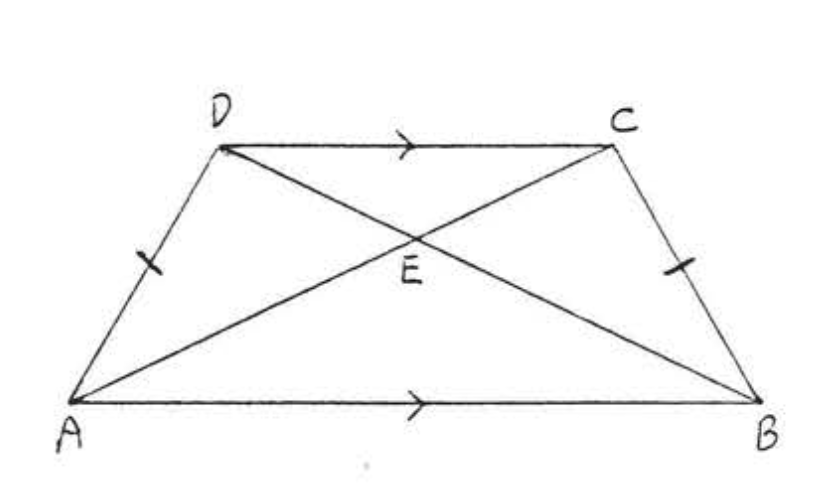
Діагоналі трикутної трапеції рівні.

На малюнку$\PageIndex{13}$, $AC = BD$

Малюнок$\PageIndex{13}$. The diagonals $AC$ and $BD$ are equal.

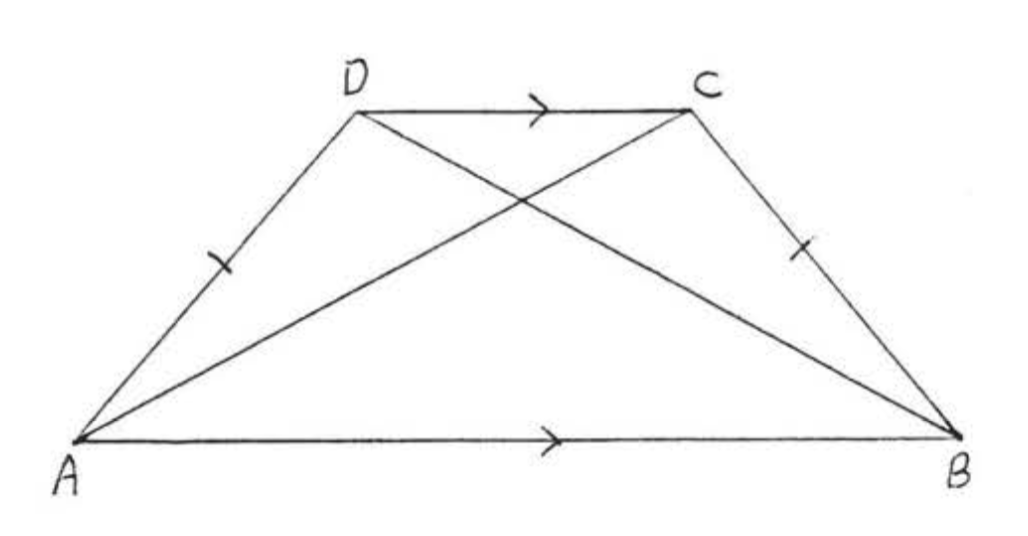
Доказ

$BC = AD$, наведено,$\angle ABC = \angle BAD$ оскільки вони є базовими кутами рівнобедрених трапецій$ABCD$ (теорема$\PageIndex{4}$). $AB = BA$, identity. Therefore $\triangle ABC \cong \triangle BAD$ by $SAS = SAS$. So $AC = BD$ because they are corresponding sides of the congruent triangles.

Приклад$\PageIndex{6}$

Знайти$x$, якщо$AC = \dfrac{2}{x}$ і$BD = 3 - x$:

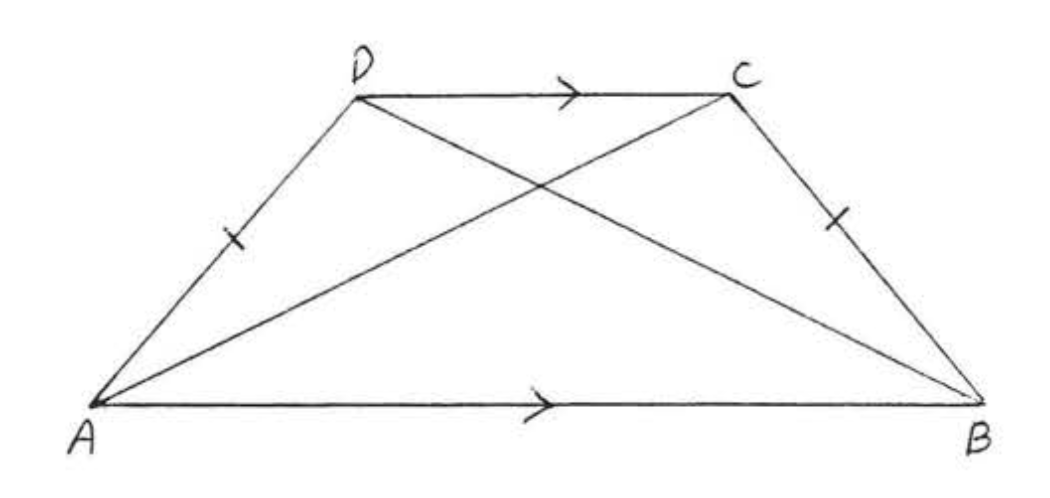
Рішення

За теоремою$\PageIndex{5}$,

$\begin{array} {rcl} {AC} & = & {BD} \\ {\dfrac{2}{x}} & = & {3 - x} \\ {(x)\dfrac{2}{x}} & = & {(3 - x)(x)} \\ {2} & = & {3x - x^2} \\ {x^2 - 3x + 2} & = & {0} \\ {(x - 1)(x - 2)} & = & {0} \end{array}$

$\begin{array} {rcl} {x - 1} & = & {0} \\ {x} & = & {1} \end{array}$$\begin{array} {rcl} {x - 2} & = & {0} \\ {x} & = & {2} \end{array}$

Перевірте,$x = 1$:

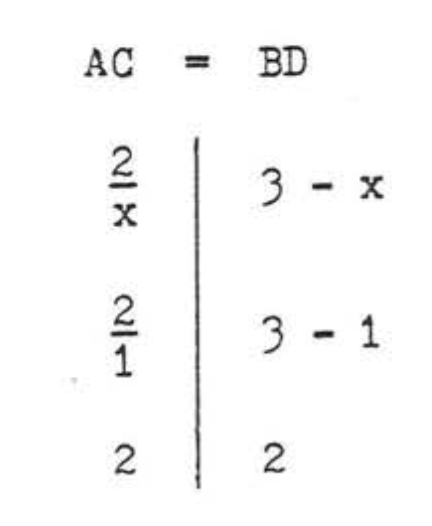
Перевірте,$x = 2$:

Відповідь:$x = 1$ or $x = 2$.

РЕЗЮМЕ

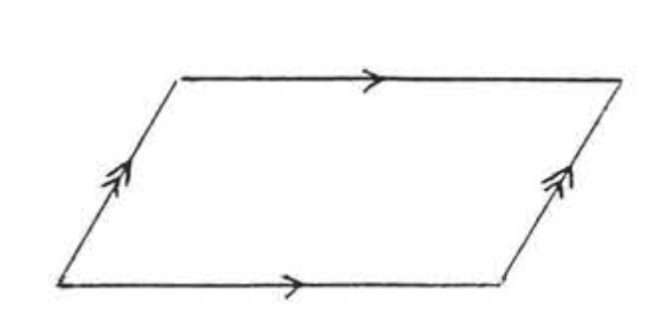
ПАРАЛЕЛОГРАМ

Чотирикутник, в якому протилежні сторони паралельні.

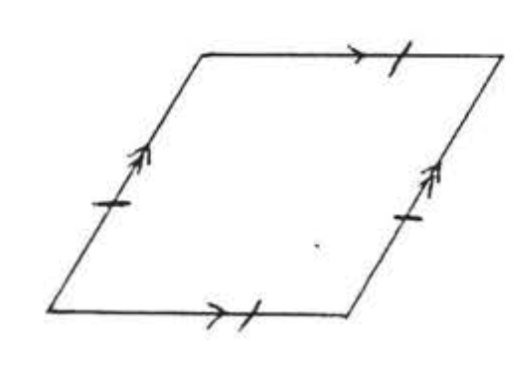
РОМБ

Паралелограм, в якому всі сторони рівні.

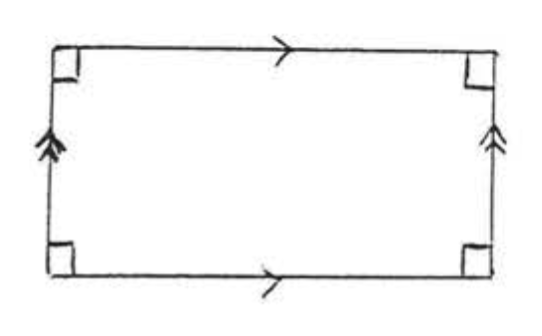
ПРЯМОКУТНИК

Паралелограм, в якому всі кути рівні$90^{\circ}$.

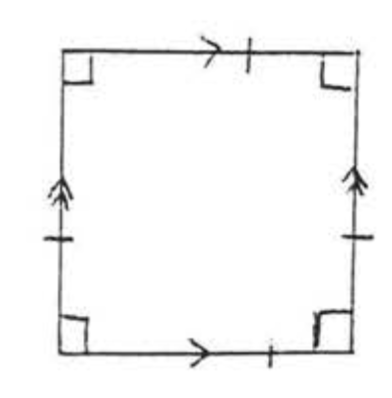
КВАДРАТ

Паралелограм, який є одночасно ромбом і прямокутником.

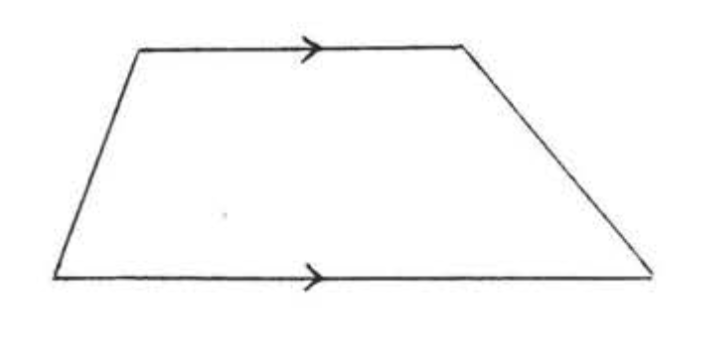
ТРАПЕЦІЯ

Чотирикутник з однією парою паралельних сторін.

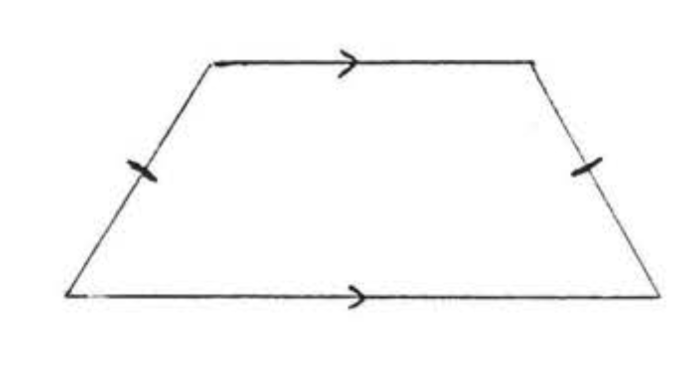
РІВНОБЕДРЕНИЙ ТРАПЕЦІЇ

Трапеція, в якій непаралельні сторони рівні.

ВЛАСТИВОСТІ ЧОТИРИКУТНИКІВ

	Протилежні сторони паралельні	Протилежні сторони рівні	протилежні кути	Діагоналі розсікають один одного	Діагоналі рівні	Діагоналі перпендикулярні	Діагоналі бісекції кутів	Всі сторони рівні	Всі кути рівні
Паралелограм	ТАК	ТАК	ТАК	ТАК	-	-	-	-	-
Ромб	ТАК	ТАК	ТАК	ТАК	-	ТАК	ТАК	ТАК	-
Прямокутник	ТАК	ТАК	ТАК	ТАК	ТАК	-	-	-	ТАК
Трапеція	*	-	-	-	-	-	-	-	-
Рівнобедрений трапеція	*	*	-	-	ТАК	-	-	-	-

*Тільки одна пара.

Проблеми

Для кожного з наступних станів будь-які теореми, які використовуються при отриманні вашої відповіді.

1. Знайти$w, x, y$, і$z$:

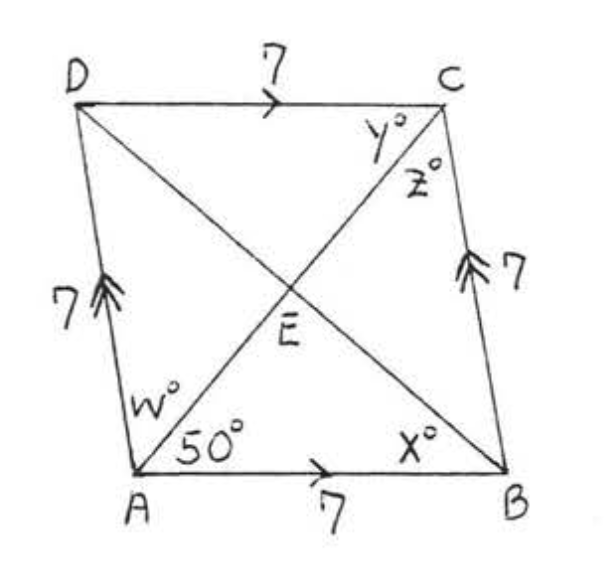
2. Знайти$w, x, y$, і$z$:

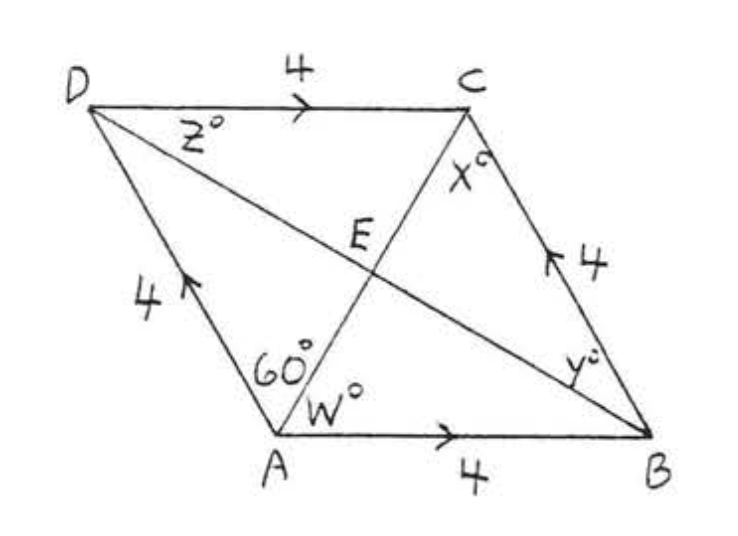
3. Знайти$x$ і$y$:

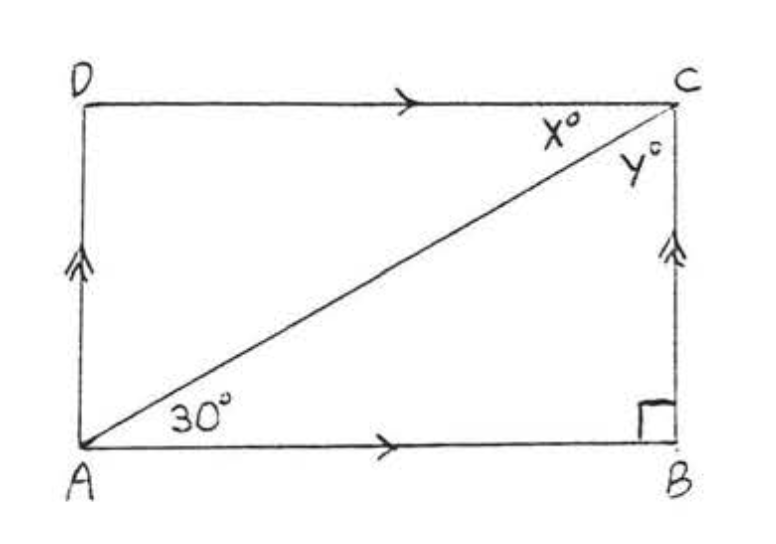
4. Знайти$x$ і$y$:

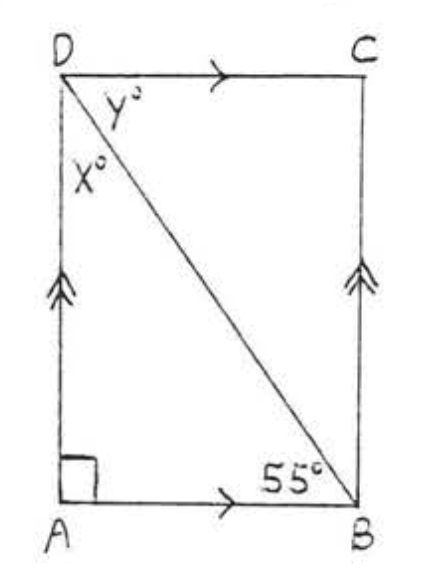
5. Знайти$x, y, z, AC$ і$BD$:

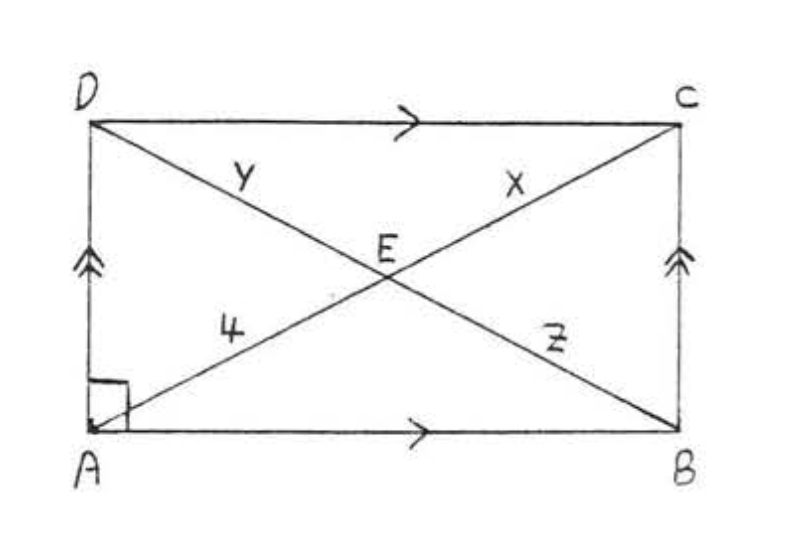
6. Знайти$x, y$, і$z$:

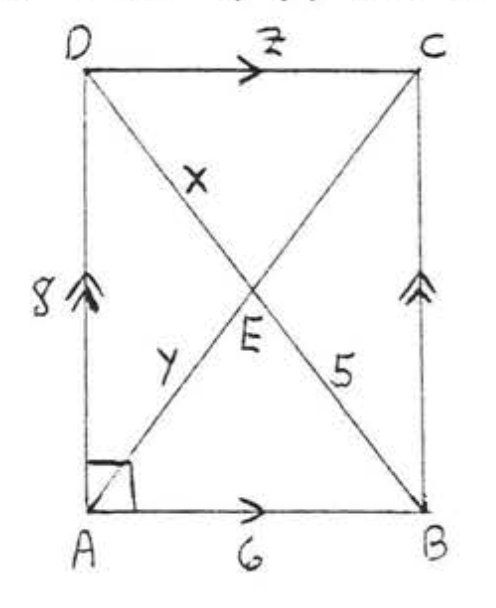
7. Знайти$x, y$, і$z$:

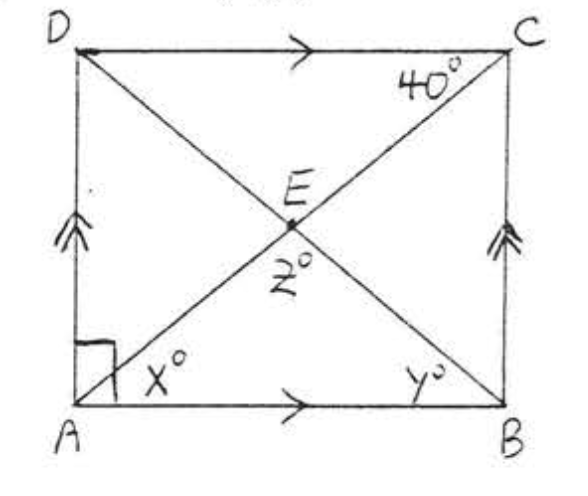
8. Знайти$x, y$, і$z$:

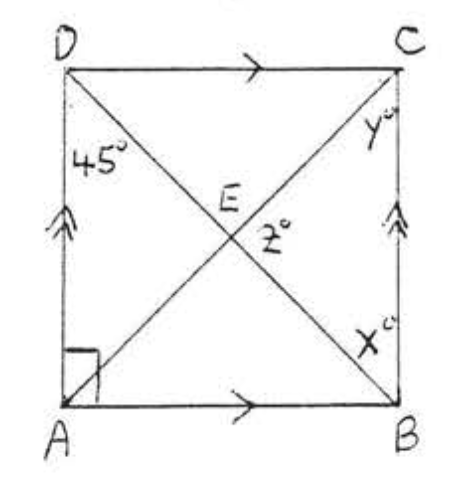
9. Знайти$x$, якщо$AC = \dfrac{3}{x}$ і$BD = 4x - 1$:

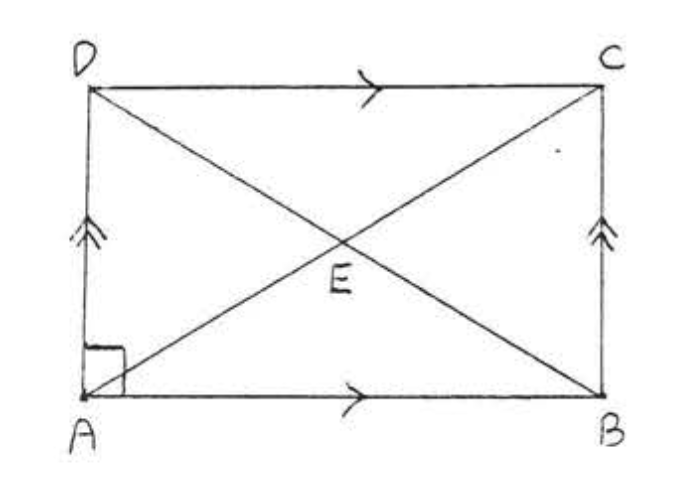
10. Знайти$x$ і$y$:

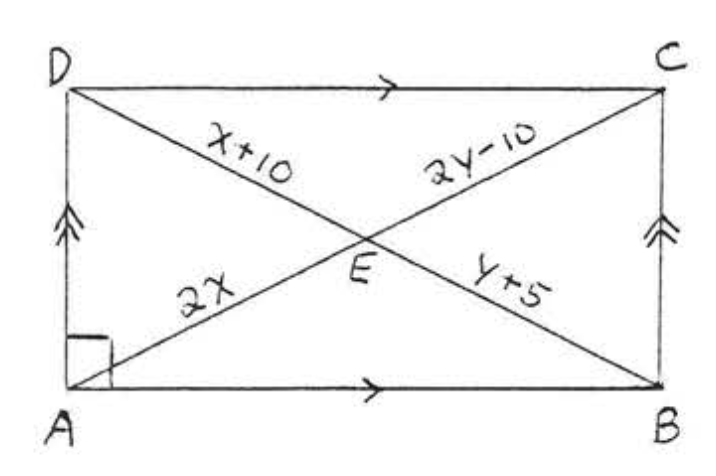
11. Знайти$x, y$, і$z$:

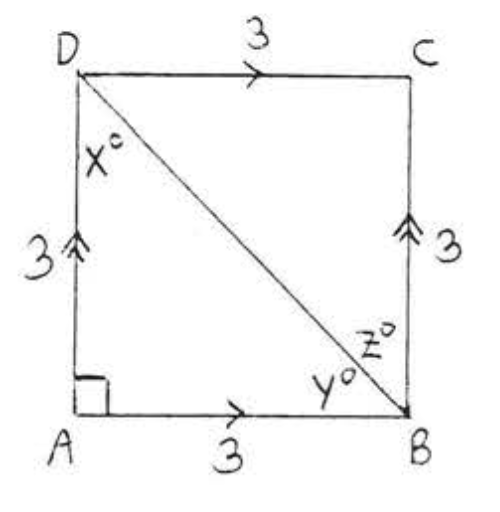
12. Знайти$x, y$, і$z$:

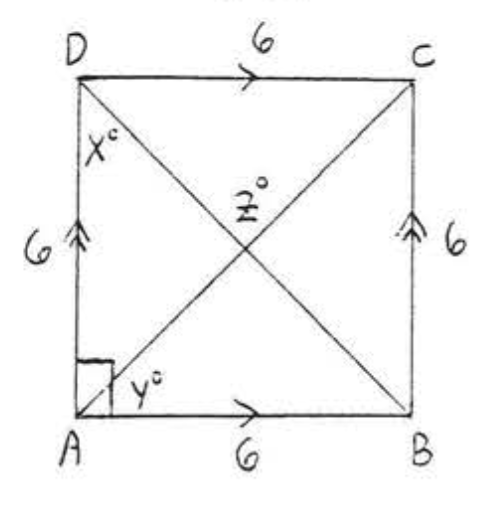
13. Знайти$x, y$, і$z$:

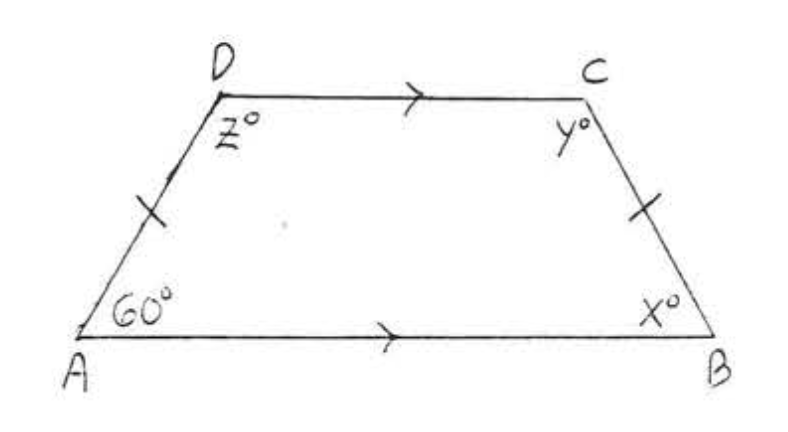
14. Знайти$x, y$, і$z$:

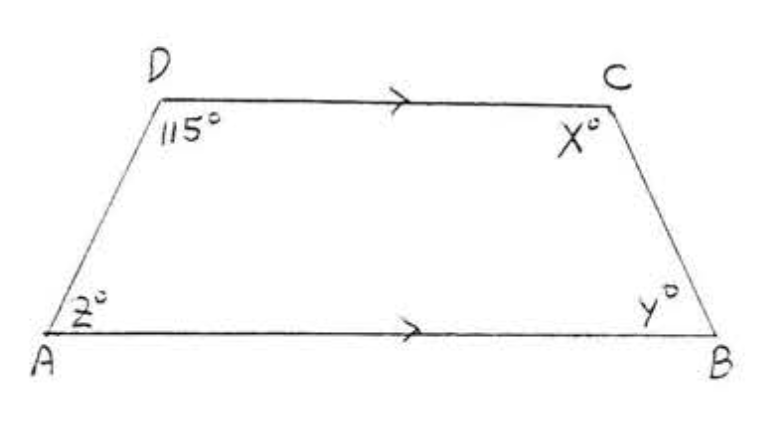
15. Знайти$x$ і$y$:

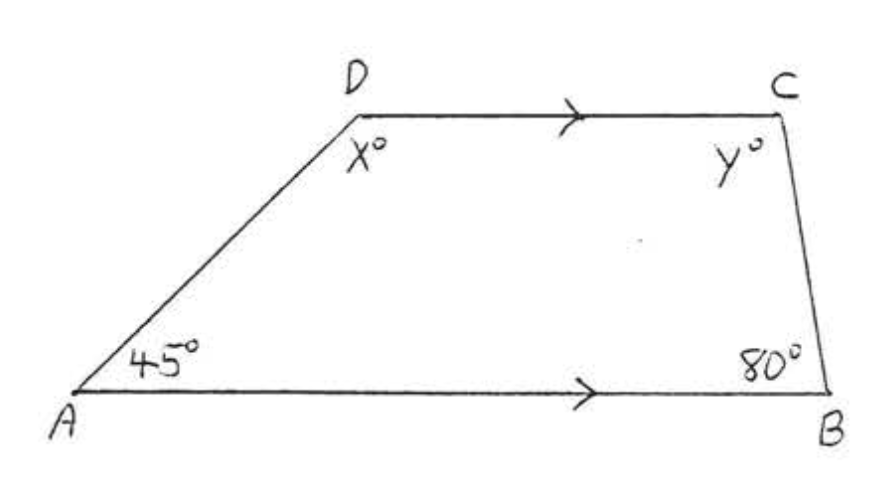
16. Знайти$x, y, \angle A, \angle B, \angle C$, і$\angle D$:

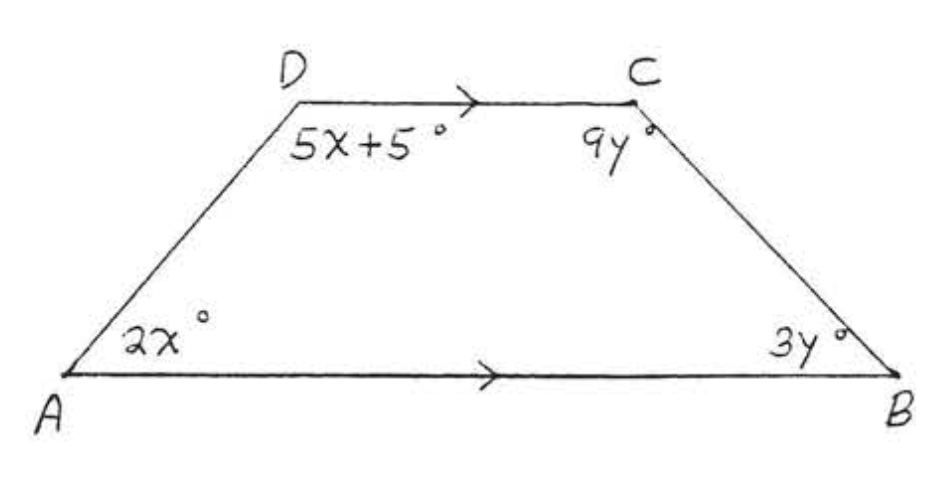
17. Знайти$w, x, y$, і$z$:

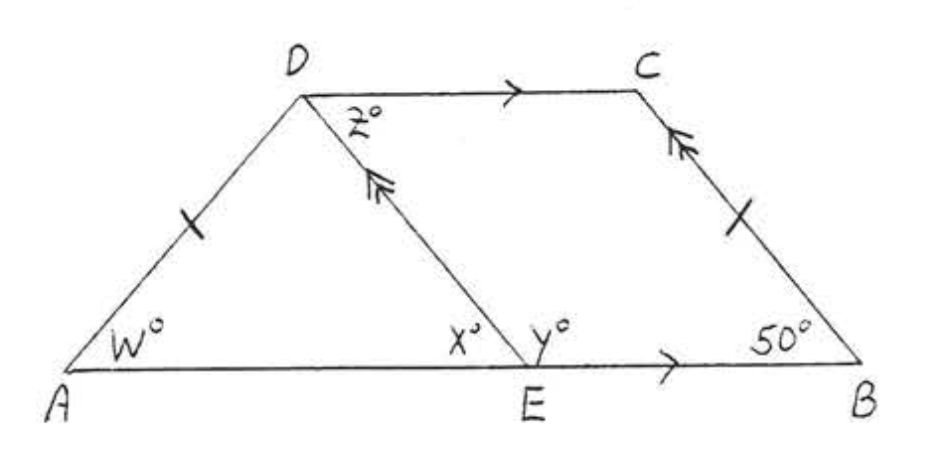
18. Знайти$x, y$, і$z$:

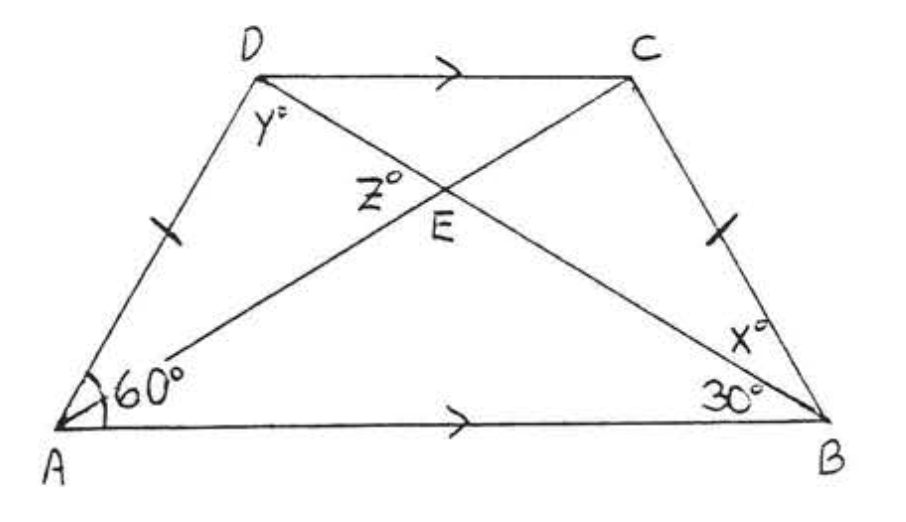
19. Знайти$x$, якщо$AC = x^2 - 13$ і$BD = 2x + 2$:

20. Знайти$x$,$AC$ і$BD$: