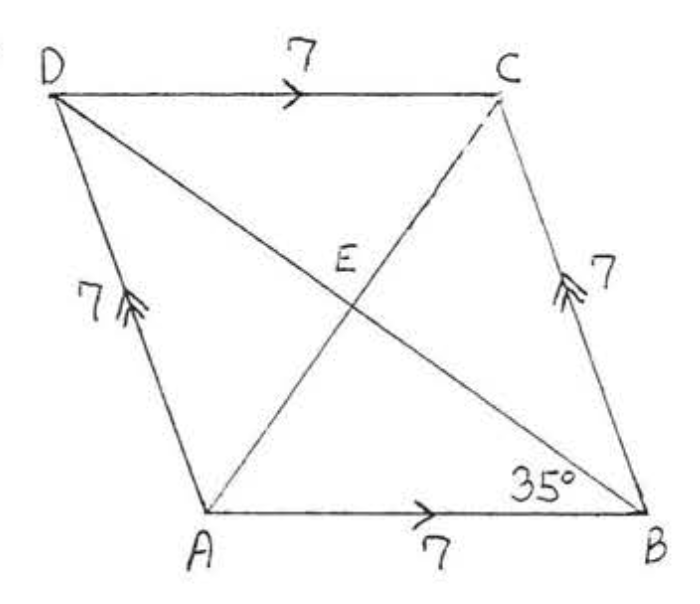
6.4: Площа ромба

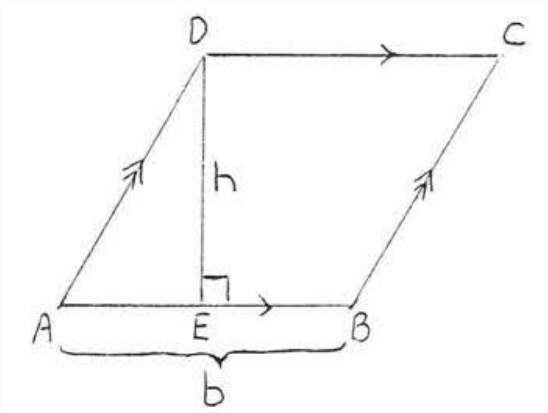
Площа ромба можна знайти, скориставшись формулою площі паралелограма$A=bh$, так як ромб - це особливий вид паралелограма (рис.$\PageIndex{1}$). Однак, якщо діагоналі відомі, замість неї можна використовувати наступну формулу (рис.$\PageIndex{2}$):

Малюнок$\PageIndex{1}$: Площа Томб$ABCD$ є$bh$. Малюнок$\PageIndex{2}$: Площа ромба$ABCD$ дорівнює$\dfrac{1}{2} d_1d_2$

Теорема$\PageIndex{1}$

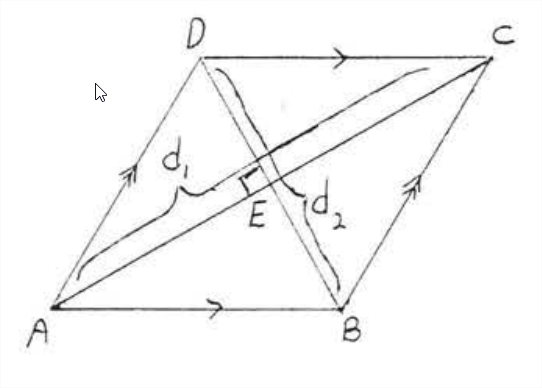
Площа ромба - половина добутку діагоналей.

$$A=\dfrac{1}{2} a_{1} a_{2}$$

Доказ

Посилаючись на малюнок$\PageIndex{2}$,

Площа$\triangle ABC$ =$\dfrac{1}{2} bh = \dfrac{1}{2} (AC)(BE) = \dfrac{1}{2} d_1 (\dfrac{1}{2} d_2) = \dfrac{1}{4} d_1d_2$.

Площа$\triangle ADC$ =$\dfrac{1}{2} bh = \dfrac{1}{2} (AC)(DE) = \dfrac{1}{2} d_1 (\dfrac{1}{2} d_2) = \dfrac{1}{4} d_1d_2$.

Площа ромба$ABCD$ = Площа$\triangle ABC$ + Площа$\triangle ADC$ =\ dfrac {1} {4} d_1d_2 +\ dfrac {1} {4} d_1d_2 =\ dfrac {1} {2} d_1d_2\).

Приклад$\PageIndex{1}$

Знайдіть площу ромба:

Рішення

$A=\dfrac{1}{2} a_{1} d_{2}=\dfrac{1}{2}(8)(6)=\dfrac{1}{2}(48)=24$

Відповідь: 24.

Приклад$\PageIndex{2}$

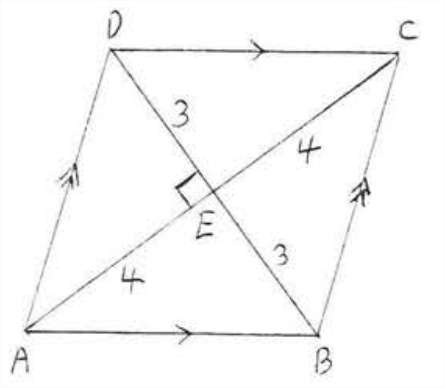
Знайдіть площу і периметр ромба:

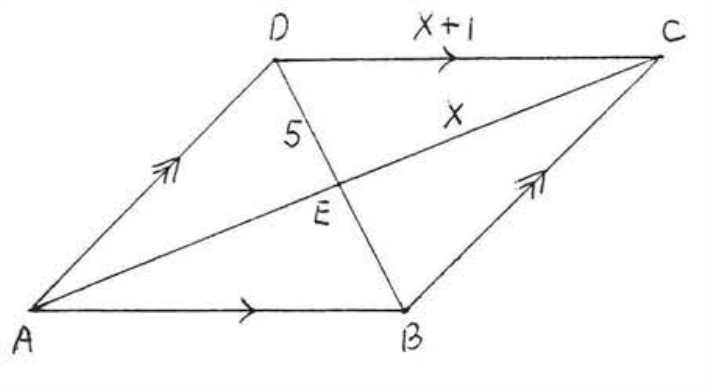
Рішення

Діагоналі ромба перпендикулярні, так$\triangle CDE$ це прямокутний трикутник. Тому ми можемо застосувати теорему Піфагора.

$$\begin{array} {rcl} {5^2 + x^2} & = & {(x+1)^2} \\ {25 + x^2} & = & {x^2 + 2x + 1} \\ {24} & = & {2x} \\ {12} & = & {x} \end{array}$$

$d_1 = 12 + 12 = 24$. $d_2 = 5 + 5 =10$. $A = \dfrac{1}{2}d_1d_2 = \dfrac{1}{2} (24)(10) = 120$.

$CD = x + 1 = 12 + 1= 13$.

Периметр = 13 + 13 + 13 + 13 = 52.

Відповідь:$A = 120$,$P = 52$.

Приклад$\PageIndex{3}$

Знайдіть площу ромба:

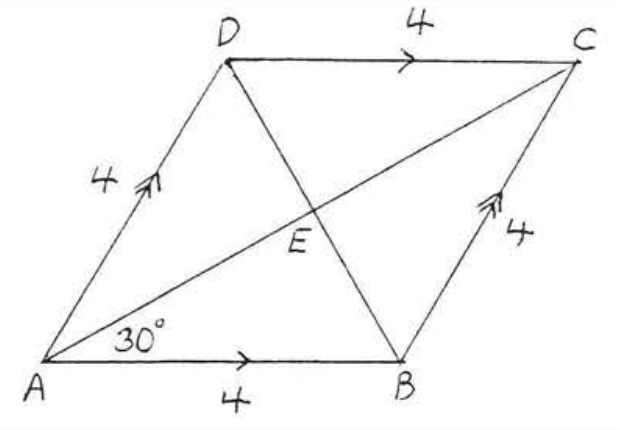
Рішення

Як і в прикладі 4.5.6 розділу 4.5, отримуємо$AC = 4\sqrt{3}$ і$BD = 4$, Площа =$\dfrac{1}{2} d_1d_2 = \dfrac{1}{2} (AC)(BD) = \dfrac{1}{2}(4\sqrt{3})(4) = 8\sqrt{3}$.

Відповідь:$A = 8\sqrt{3}$.

Проблеми

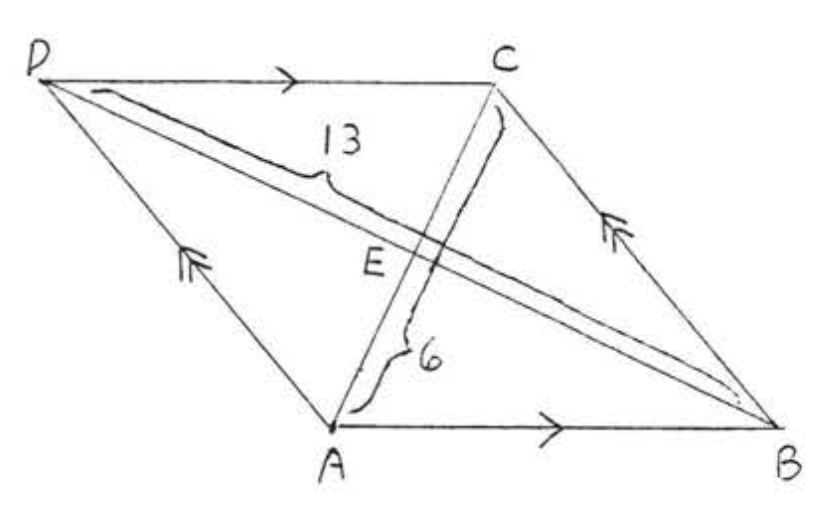
1 - 2. Знайдіть площу ромба:

1.

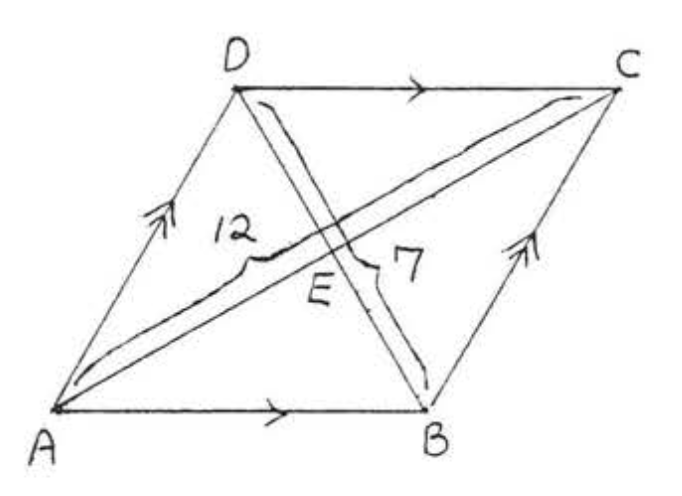
2.

3 - 8. Знайдіть площу і периметр ромба:

3.

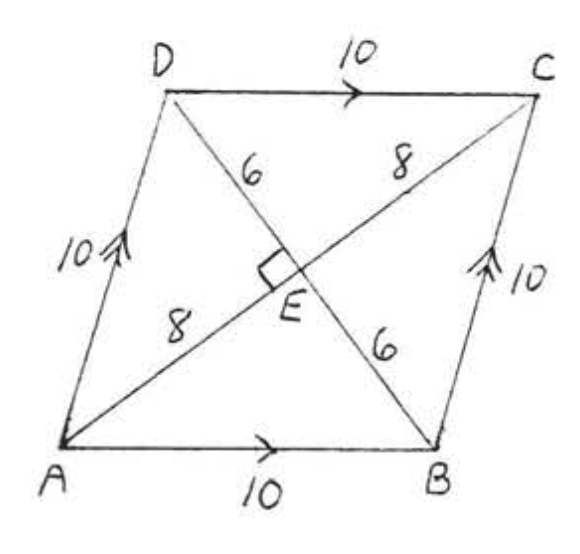
4.

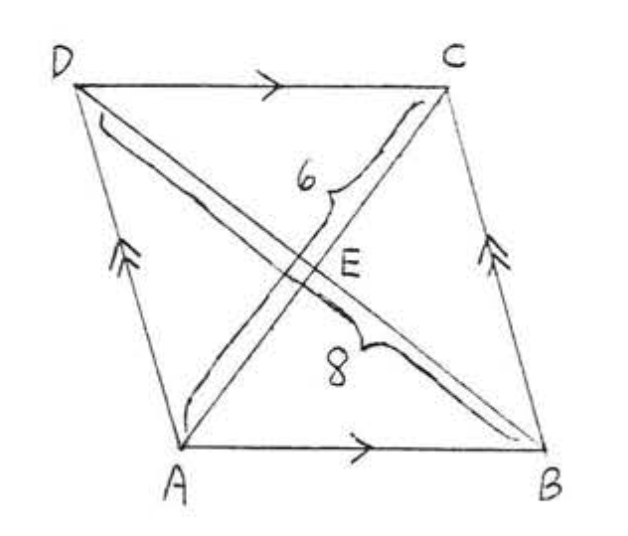
5.

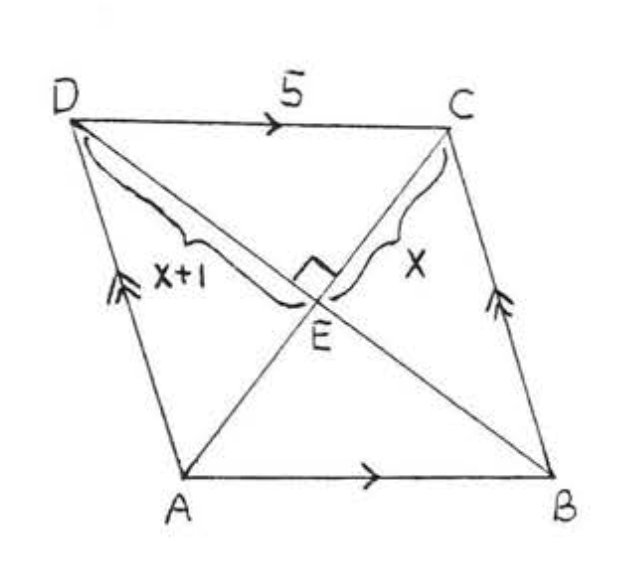
6.

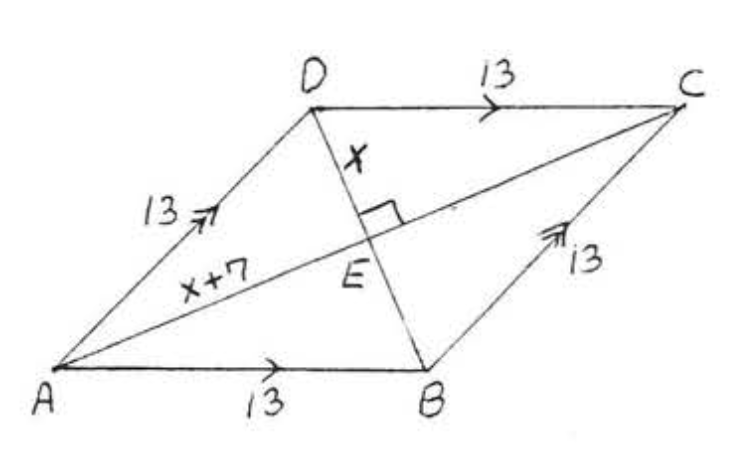
7.

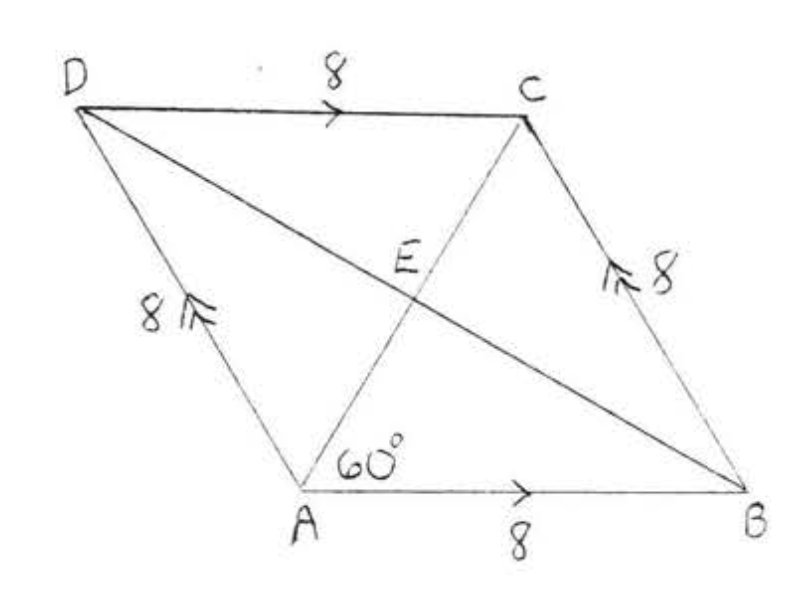
8.

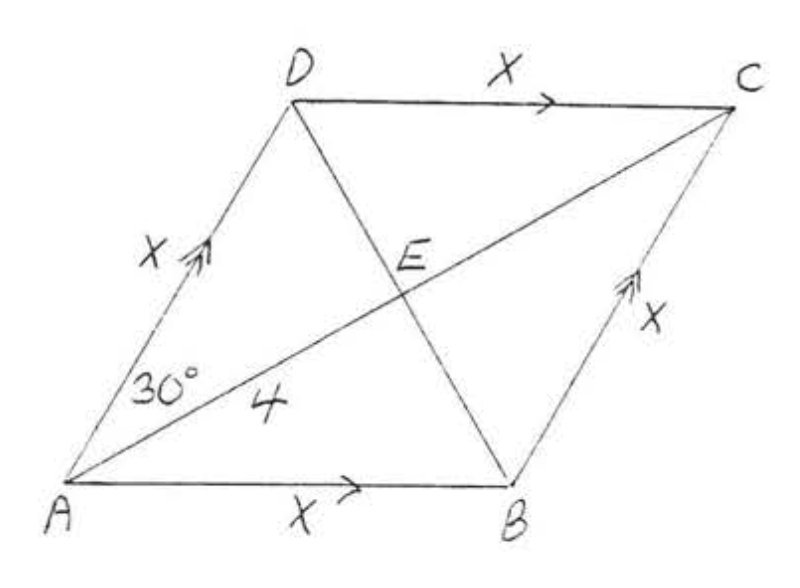
9 - 10. Знайдіть площу до найближчої десятої:

9.

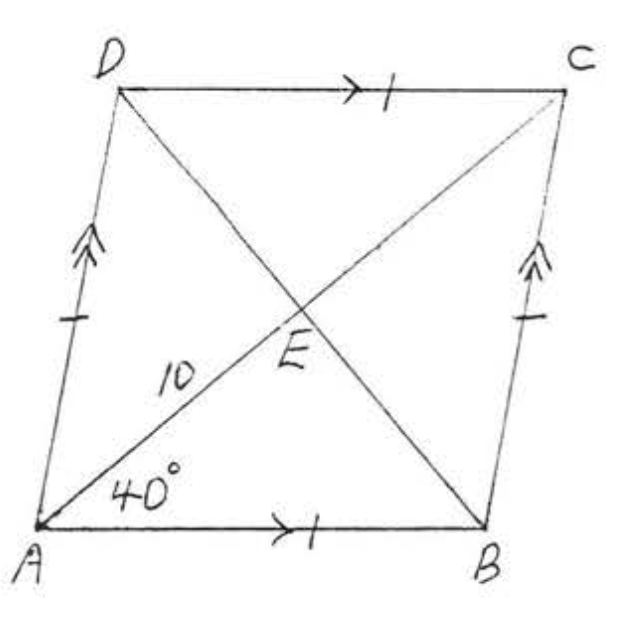
10.