Skip to main content
LibreTexts - Ukrayinska

13.2: Трикутники

  1. Last updated
  2. Save as PDF
  • Page ID
    77955

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Я почну з геометричної теореми, що включає трикутники, яка буде корисна в міру просування до нашої мети обчислення орбітальних елементів.


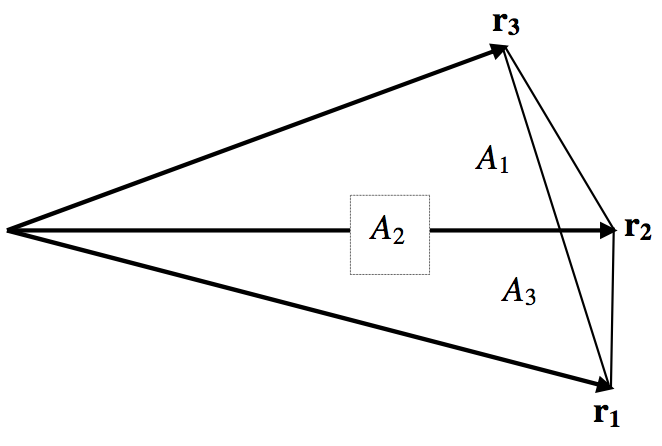
    Малюнок 13.1.png
    \(\text{FIGURE XIII.1}\)

    \(\text{XIII.1}\)На малюнку показані три компланарних вектора. Чітко можна висловити\(\textbf{r}_2\) як лінійну комбінацію двох інших. Тобто, повинна бути можливість знайти коефіцієнти такі, що

    \[\textbf{r}_2 = a_1 \textbf{r}_1 + a_3 \textbf{r}_3 . \label{13.2.1}\]

    Позначення, яке я збираюся використовувати, виглядає наступним чином:

    • Площа трикутника, утвореного з'єднанням кінчиків\(\textbf{r}_2\) і\(\textbf{r}_3\) є\(A_1\).
    • Площа трикутника, утвореного з'єднанням кінчиків\(\textbf{r}_3\) і\(\textbf{r}_1\) є\(A_2\).
    • Площа трикутника, утвореного з'єднанням кінчиків\(\textbf{r}_1\) і\(\textbf{r}_2\) є\(A_3\).

    Щоб знайти коефіцієнти в Equation\ ref {13.2.1}, помножте обидві сторони на\(\textbf{r}_1 \times\):

    \[\textbf{r}_1 \times \textbf{r}_2 = a_3 \textbf{r}_1 \times \textbf{r}_3 . \label{13.2.2}\]

    Два векторних добутку є паралельними векторами (кожен з них перпендикулярний площині паперу), величин\(2A_3\) і\(2A_2\) відповідно. (\(2A_3\)Це площа паралелограма, з якого вектори\(\textbf{r}_1\) і\(\textbf{r}_2\) утворюють дві сторони.)

    \[\therefore a_3 = A_3/A_2 . \label{13.2.3}\]

    Аналогічно шляхом множення обох сторін Equation\ ref {13.2.1} на\(\textbf{r}_3 \times\) це буде встановлено, що

    \[a_1 = A_1/ A_2 . \label{13.2.4}\]

    Отже, ми знаходимо, що

    \[A_2 \textbf{r}_2 = A_1 \textbf{r}_1 + A_3 \textbf{r}_3 . \label{13.2.5}\]