1.5: Трикутники
- Page ID
- 58811
Трикутник утворюється, коли три прямих відрізка пов'язані частиною площини. Відрізки лінії називаються сторонами трикутника. Точка, де зустрічаються дві сторони, називається вершиною трикутника, а утворений кут називається кутом трикутника. Символ трикутника є\(\triangle\).
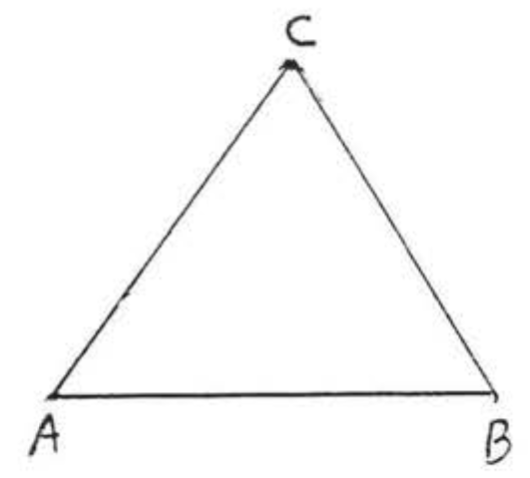
Трикутник на малюнку\(\PageIndex{1}\) позначається символом\(\triangle ABC\) (\(\triangle BCA\)або або і\(\triangle CAB\) т.д.).
- Його сторони є\(AB\),\(AC\), і\(BC\).
- Його вершини є\(A, B\), і\(C\).
- Його кути є\(\angle A\),\(\angle B\), і\(\angle C\).
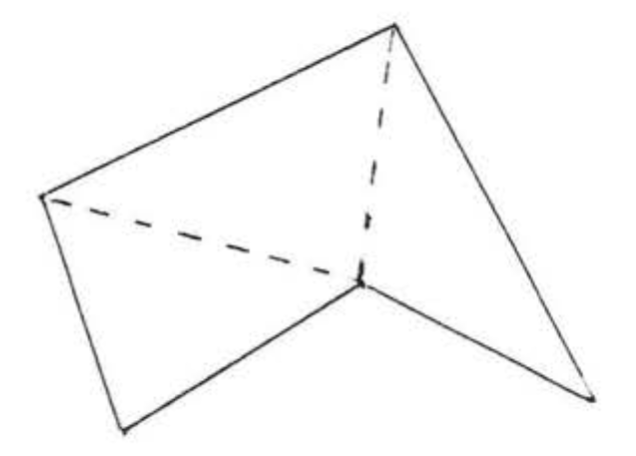
Трикутник є найважливішою фігурою в геометрії площини, Це тому, що фігури з більш ніж трьома сторонами завжди можна розділити на трикутники (рис.\(\PageIndex{2}\)). Якщо ми знаємо властивості трикутника, ми можемо поширити ці знання і на вивчення інших фігур.
Фундаментальним властивістю трикутників є наступне:
Сума кутів трикутника дорівнює\(180^{\circ}\).
На малюнку\(\triangle ABC\)\(\PageIndex{1}\), \(\angle A + \angle B + \angle C = 180^{\circ}\).
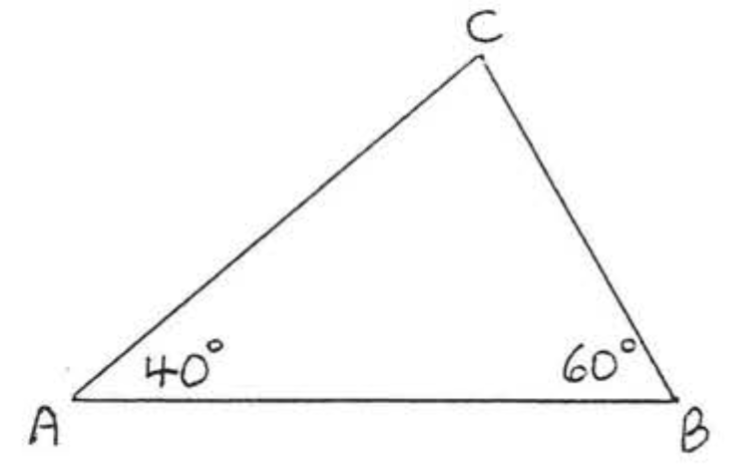
Знайти\(\angle C\):
Рішення
\[\begin{array} {rcl} {\angle A + \angle B + \angle C} & = & {180^{\circ}} \\ {40^{\circ} + 60^{\circ} + \angle C} & = & {180^{\circ}} \\ {100^{\circ} + \angle C} & = & {180^{\circ}} \\ {\angle C} & = & {180^{\circ} - 100^{\circ}} \\ {\angle C} & = & {80^{\circ}} \end{array} \nonumber\]
Відповідь:\(\angle C = 80^{\circ}\)
Доказ теореми\(\PageIndex{1}\):\(C\) Наскрізний малюнок\(DE\) паралельно\(AB\) (див. Рис.\(\PageIndex{3}\)). Зверніть увагу, що ми використовуємо паралельний постулат тут,\(\angle 1 = \angle A\) і\(\angle 3 = \angle B\) тому що вони чергуються внутрішні кути паралельних ліній, Тому\(\angle A + \angle B + \angle C = \angle 1 + \angle 3 + \angle 2 = 180^{\circ}\).

Ми можемо перевірити теорему, виміряючи кути трикутника\(\PageIndex{1}\) за допомогою транспортира і приймаючи суму, Однак жоден вимірювальний прилад не є абсолютно точним, розумно очікувати відповіді, такі як\(179^{\circ}\),\(182^{\circ}\)\(180.5^{\circ}\), і т.д Мета нашого математичного доказу полягає в тому, щоб запевнити нас, що сума кутів кожного трикутника повинна бути точно\(180^{\circ}\).
Знайти\(x\):

Рішення
\[\begin{array} {rcl} {\angle A + \angle B + \angle C} & = & {180^{\circ}} \\ {2x + 3x + 4x} & = & {180} \\ {9x} & = & {180} \\ {x} & = & {20} \end{array} \nonumber\]
Перевірка:

Відповідь:\(x = 20\).
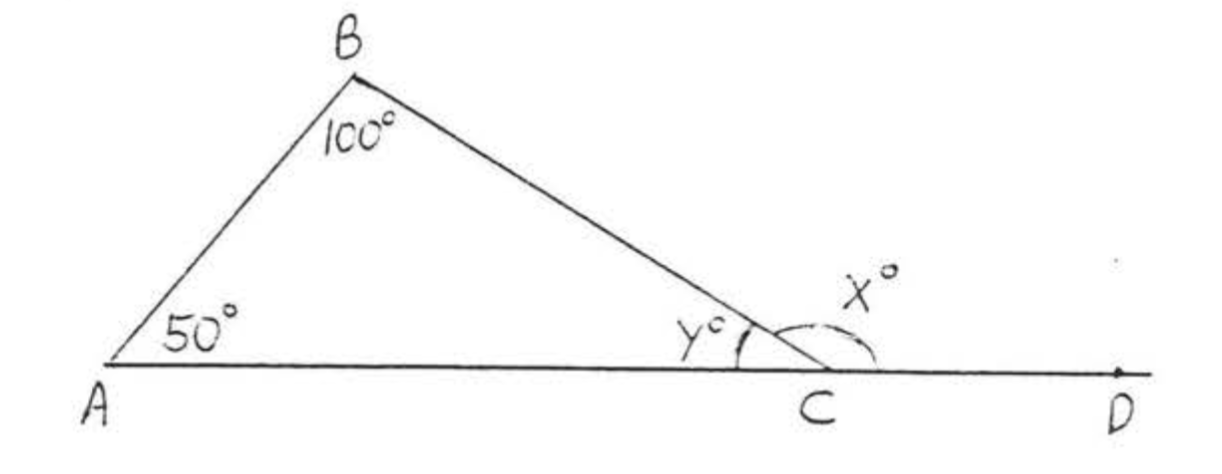
Знайти\(y\) і\(x\):
Рішення
\[\begin{array} {rcl} {50 + 100 + y} & = & {180} \\ {150 + y} & = & {180} \\ {y} & = & {180 - 150} \\ {y} & = & {30} \\ {} & & {} \\ {x} & = & {180 - 30 = 150} \end{array}\]
Відповідь:\(y = 30\),\(x = 150\).
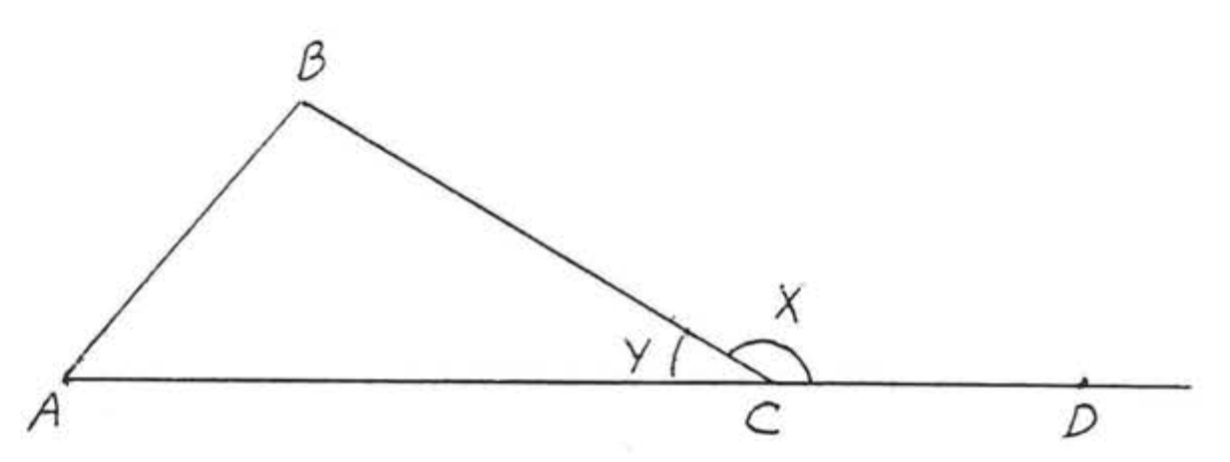
На малюнку\(\PageIndex{4}\),\(\angle x\) називається зовнішній кут\(\triangle ABC\),\(\angle A\)\(\angle B\), і\(\angle y\) називаються внутрішніми кутами\(\triangle ABC\). \(\angle A\)і\(\angle B\), як кажуть, внутрішні кути віддалені від зовнішнього кута\(\angle x\).
Результати Прикладу\(\PageIndex{3}\) припускають наступну теорему.
Зовнішній кут дорівнює сумі двох віддалених внутрішніх кутів,
На малюнку\(\PageIndex{4}\),\(\angle x = \angle A + \angle B\).
Знайти\(x\):

Рішення
Використовуючи теорему\(\PageIndex{2}\),\(x^{\circ} = 100^{\circ} + 50^{\circ} = 150^{\circ}\).
Відповідь:\(x = 150\).
Доказ теореми\(\PageIndex{2}\): Ми представляємо цей доказ у формі подвійного стовпця, з твердженнями в лівій колонці та причиною кожного твердження в правій колонці. Останнє твердження - теорема, яку ми хочемо довести.
| Заяви | причини |
| 1. \(\angle A + \angle B + \angle y = 180^{\circ}\) | 1. Сума кутів трикутника дорівнює\(180^{\circ}\). |
| 2. \(\angle A + \angle B = 180^{\circ} - \angle y\) | 2. Відніміть\(\angle y\) з обох сторін рівняння, твердження 1. |
| 3. \(\angle x = 180^{\circ} - \angle y.\) | 3. \(\angle x\)і\(\angle y\) є додатковими. |
| 4. \(\angle x = \angle A + \angle B\). | 4. Обидва\(\angle x\) (твердження 3) і\(\angle A + \angle B\) (твердження 2) рівні\(180^{\circ} - \angle y\). |
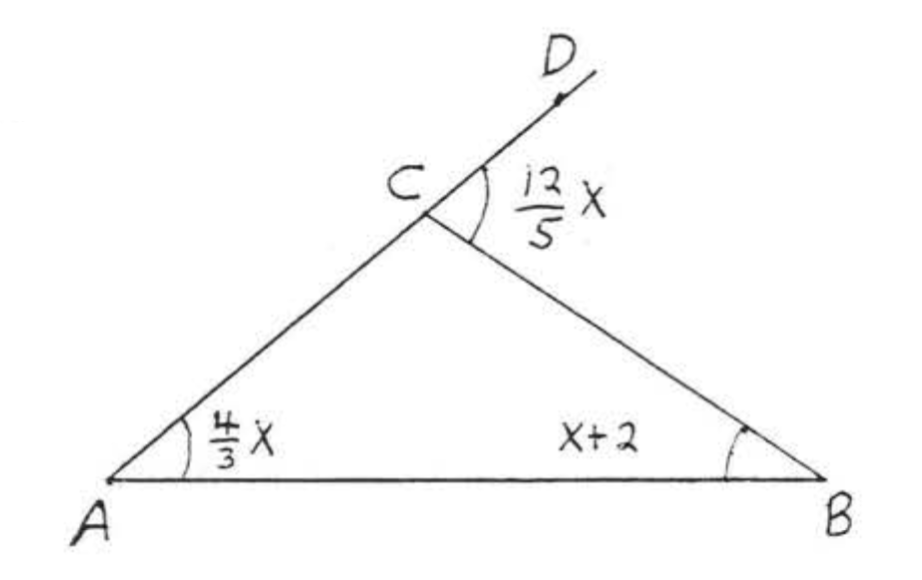
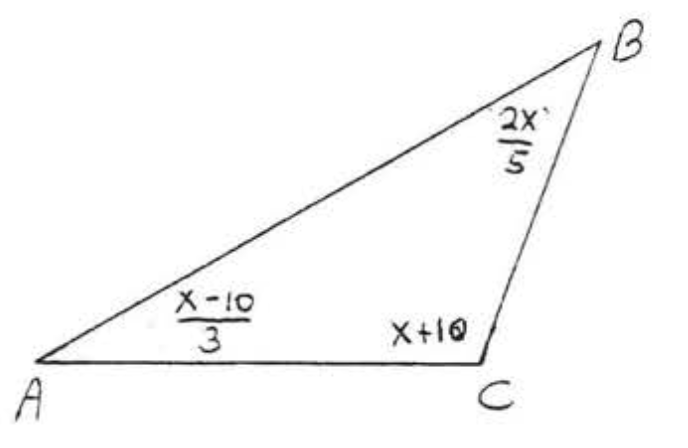
Знайти\(x\):
Рішення
\(\angle BCD\)являє собою зовнішній кут з виносними внутрішніми кутами\(\angle A\) і\(\angle B\). За теоремою\(\PageIndex{2}\),
\[\begin{array} {rcl} {\angle BCD} & = & {\angle A + \angle B} \\ {\dfrac{12}{5} x} & = & {\dfrac{4}{3} x + x + 2} \end{array}\]
Найменш спільний знаменник (1, c, d) дорівнює 15.
\[\begin{array} {rcl} {\begin{array} {c} {^3} \\ {(\cancel{15})} \end{array} \dfrac{12}{\cancel{5}} x} & = & {\begin{array} {c} {^3} \\ {(\cancel{15})} \end{array} \dfrac{4}{\cancel{3}} x + (15)x + (15)(2)} \\ {36x} & = & {20x + 15x + 30} \\ {36x} & = & {35x + 30} \\ {36x - 35x} & = & {30} \\ {x} & = & {30} \end{array} \nonumber\]
Перевірка:
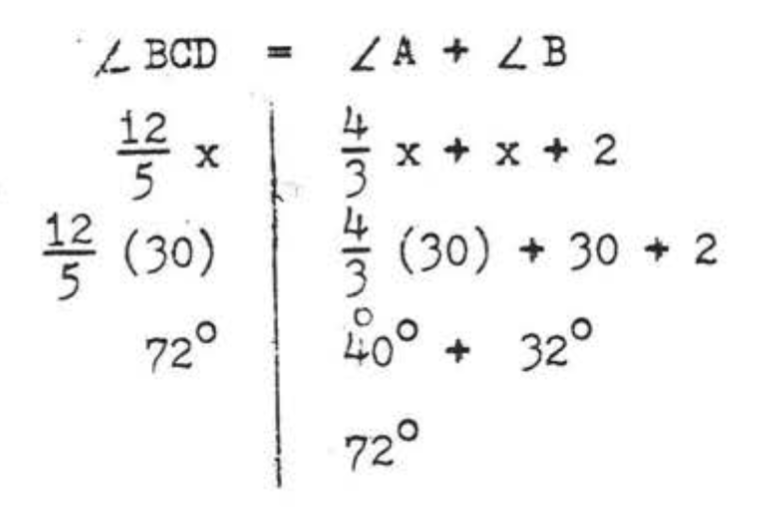
Відповідь:\(x = 30\).
Нашу роботу над сумою кутів трикутника можна легко розширити і на інші фігури:
Знайти суму кутів чотирикутника (чотиристороння фігура),
Рішення
Розділіть чотирикутник на два трикутники, як показано на малюнку,
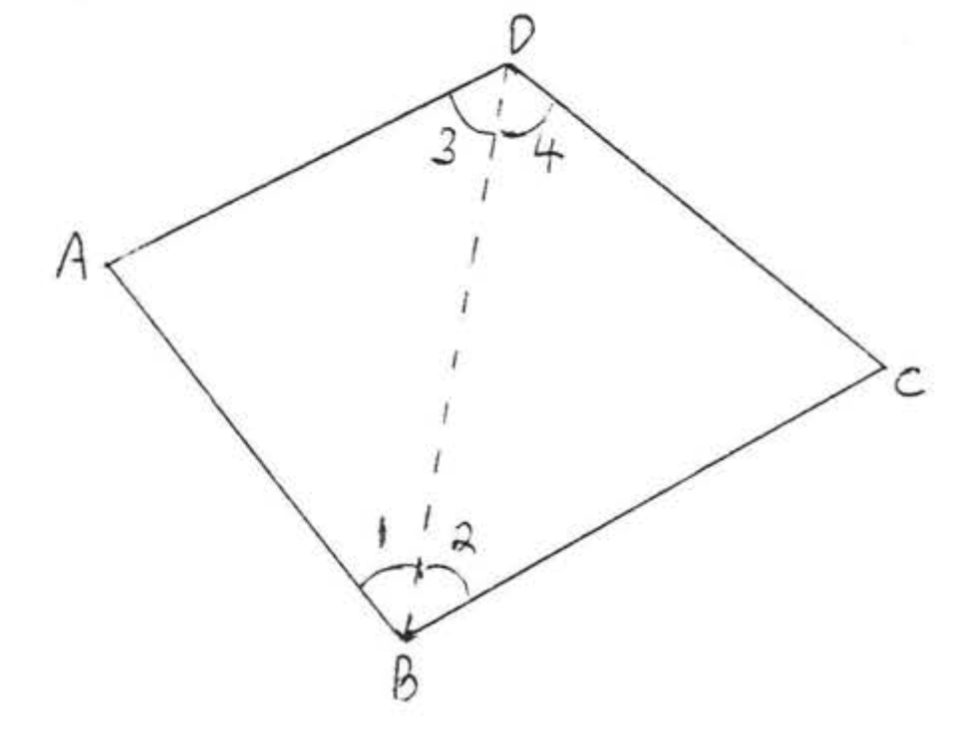
\[\begin{array} {rcl} {\angle A + \angle B + \angle C + \angle D} & = & {\angle A + \angle 1 + \angle 3 + \angle 2 + \angle 4 + \angle C} \\ {} & = & {180^{\circ} + 180^{\circ}} \\ {} & = & {360^{\circ}} \end{array} \nonumber\]
Відповідь:\(360^{\circ}\).
Знайти суму кутів п'ятикутника (п'ятигранної фігури).
Рішення
Розділіть п'ятикутник на три трикутника, як показано, сума дорівнює сумі кутів трьох трикутників =\((3)(180^{\circ}) = 540^{\circ}\).
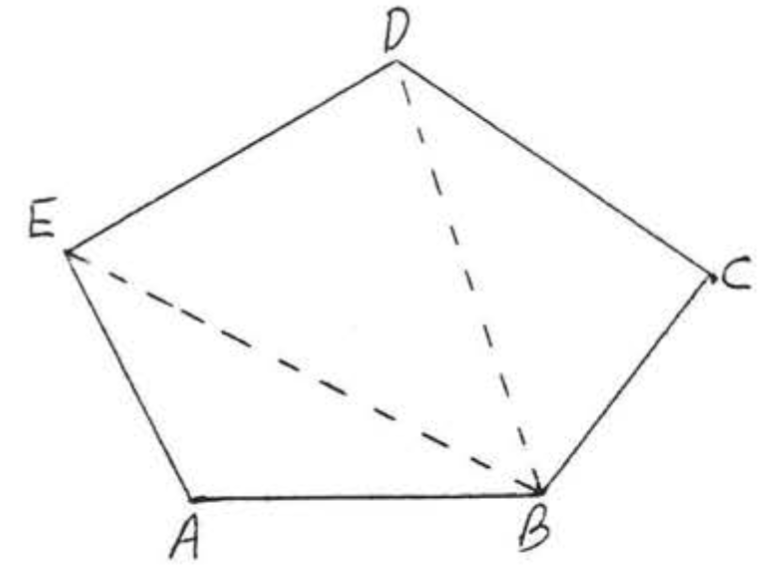
Відповідь:\(540^{\circ}\).
Існує ще один простий принцип, який ми виведемо з теореми\(\PageIndex{1}\), Розглянемо два трикутника на малюнку\(\PageIndex{5}\).

Нам дано, що\(\angle A = \angle D = 60^{\circ}\) і\(\angle B = \angle E = 40^{\circ}\). Короткий розрахунок показує, що ми також повинні мати\(\angle C = \angle F = 80^{\circ}\). Це говорить про наступну теорему:
Якщо два кути одного трикутника рівні відповідно двом кутам іншого трикутника, то і інші їх кути теж рівні.
На малюнку\(\PageIndex{6}\), if \(\angle A = \angle D\) and \(\angle B = \angle E\) then \(\angle C = \angle F\).
- Доказ
-
\(\angle C = 180^{\circ} - (\angle A + \angle B) = 180^{\circ} - (\angle D + \angle E) = \angle F\).

Малюнок\(\PageIndex{6}\). \(\angle A = \angle D\) and \(\angle B = \angle E\).
Наша теорема\(\PageIndex{1}\), яка стверджує, що сума кутів трикутника є\(180^{\circ}\), є одним з найважливіших наслідків паралельного постулату, Тому одним із способів перевірки істинності паралельного постулату (див. Історичну записку в розділі 1.4) є перевірка Правда теореми\(\PageIndex{1}\), Це насправді спробував німецький математик, астроном і фізик, Карл Фрідріх Гаусс (1777 - 1855). (Це той самий Гаусс, ім'я якого використовується як одиниця виміру в теорії магнетизму), Гаусс виміряв суму кутів трикутника, утвореного трьома гірськими вершинами Німеччини, знайшов суму кутів на 14,85 секунди більше\(180^{\circ}\) (60 секунд 1 хвилина, 60 хвилин = 1 градус). Однак це невелике перевищення могло бути пов'язано з експериментальною помилкою, тому сума могла бути насправді\(180^{\circ}\).
Окрім експериментальної помилки, існує ще одна складність, пов'язана з перевіркою теореми про кутову суму. Згідно неевклідової геометрії Лобачевського сума кутів трикутника завжди менше\(180^{\circ}\). У неевклідової геометрії Рімана сума кутів завжди більше, ніж\(180^{\circ}\), Однак в обох випадках різниця від\(180^{\circ}\) незначна, якщо трикутник не дуже великий, Жодна теорія не говорить нам точно, наскільки великий такий трикутник повинен бути, Навіть якщо ми виміряли кути дуже великий трикутник, як один, утворений трьома зірками, і виявив, що сума не відрізняється від\(180^{\circ}\), ми могли б тільки сказати, що теорема про суму кута і паралельний постулат, мабуть, вірні для цих великих відстаней, Ці відстані все ще можуть бути занадто малі, щоб ми могли визначити, яка геометрична система найкраще описує всесвіт в цілому,
Проблеми
1 - 12. Знайдіть\(x\) і всі відсутні кути кожного трикутника:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13 - 14. Знайти\(x, y\), і\(z\):
13. 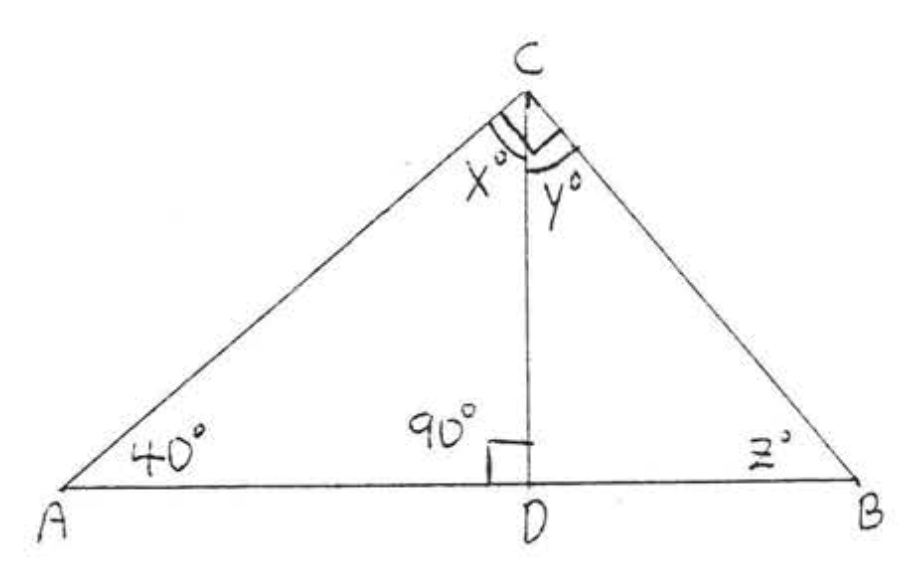 14.
14. 
15 - 20. Знайти\(x\):
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21. Знайти суму кутів шестикутника (6-гранна фігура).
22. Знайти суму кутів восьмикутника (8-гранна фігура).
23 - 26. Знайти\(x\):
23.  24.
24. 
25.  26.
26. 
