1.3: Кутові класифікації
- Page ID
- 58803
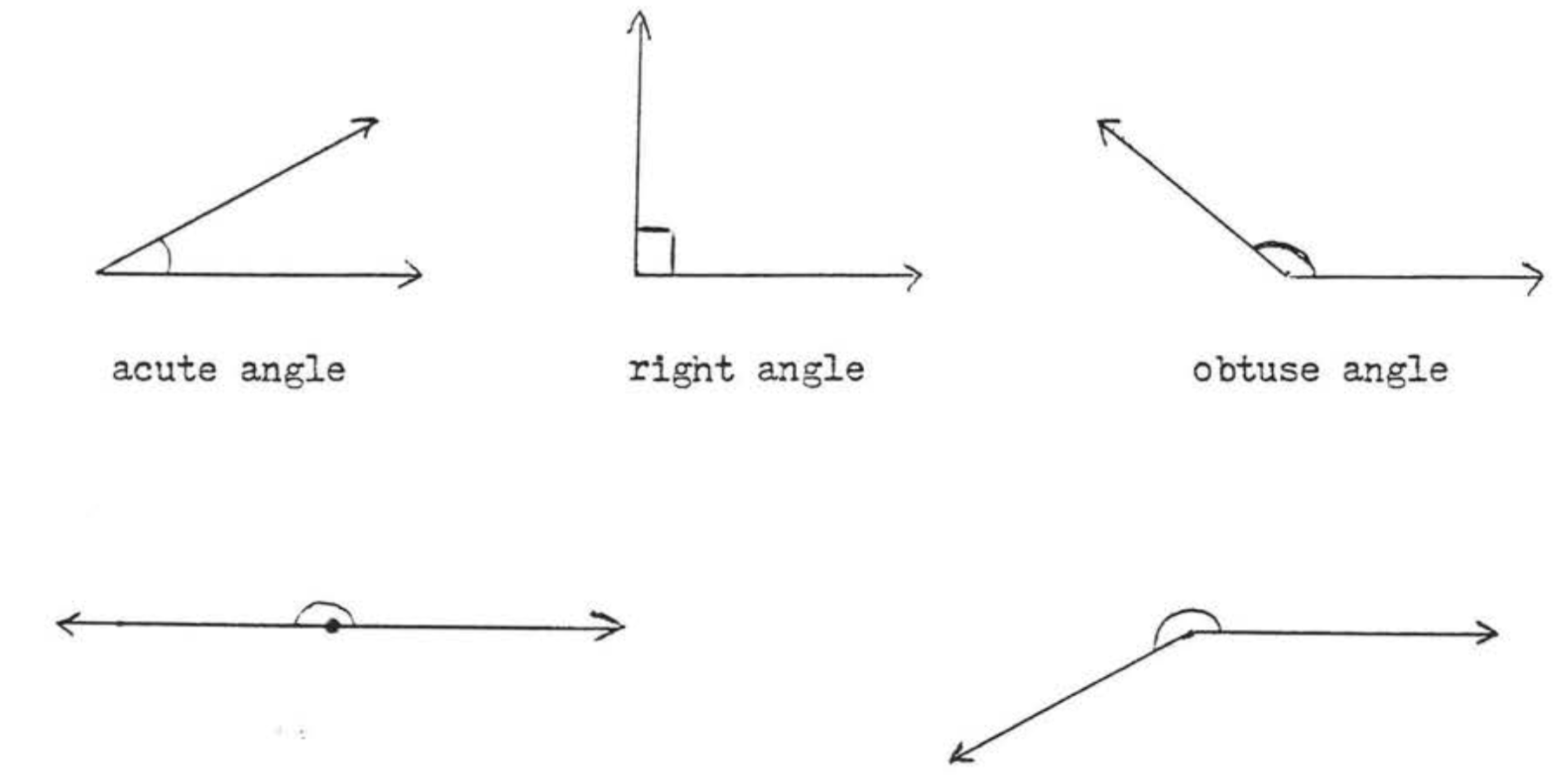
Кути класифікуються за їх мірками наступним чином:
- Гострий кут - це кут, міра якого знаходиться між\(0^{\circ}\) і\(90^{\circ}\).
- Прямим кутом називається кут, міра якого є\(90^{\circ}\). Ми часто використовуємо маленький квадрат, щоб позначити прямий кут.
- Тупий кут - це кут, міра якого знаходиться між\(90^{\circ}\) і\(180^{\circ}\).
- Прямий кут - це кут, міра якого є\(180^{\circ}\). Прямий кут - це всього лише пряма лінія, одна з її точок позначена як вершина.
- Рефлекторний кут - це кут, міра якого більше\(180^{\circ}\).
Зверніть увагу, що кут можна виміряти двома способами. На малюнку\(\PageIndex{2}\),\(\angle ABC\) це рефлекс\(240^{\circ}\) або тупий кут в\(120^{\circ}\) залежності від того, як він вимірюється. Якщо не вказано інше, ми завжди будемо вважати, що кут має міру менше\(180^{\circ}\).

Лінії перпендикулярні, якщо вони зустрічаються, утворюючи прямі кути. На малюнку\(\PageIndex{3}\),\(\overleftrightarrow{AB}\) перпендикулярно\(\overleftrightarrow{CD}\). Символ перпендикуляра є\(\perp\) і пишемо\(\overleftrightarrow{AB} \perp \overleftrightarrow{CD}\).
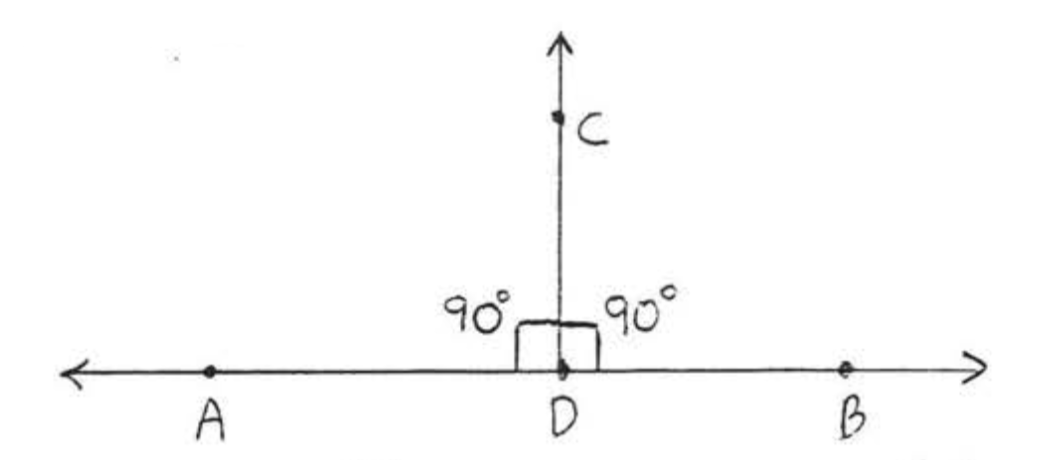
Перпендикулярна бісектриса відрізка лінії - це лінія, перпендикулярна відрізку лінії в його середній точці, На малюнку\(\PageIndex{4}\),\(\overleftrightarrow{CD}\) є перпендикулярною бісектриса\(AB\).

Два кути називаються взаємодоповнюючими, якщо сума їх мір дорівнює\(90^{\circ}\). Кожен кут називається доповненням іншого. Наприклад, кути\(60^{\circ}\) і\(30^{\circ}\) є взаємодоповнюючими.

Знайдіть доповнення\(40^{\circ}\) кута.
Рішення
\(90^{\circ} - 40^{\circ} = 50^{\circ}\).
Відповідь:\(50^{\circ}\).
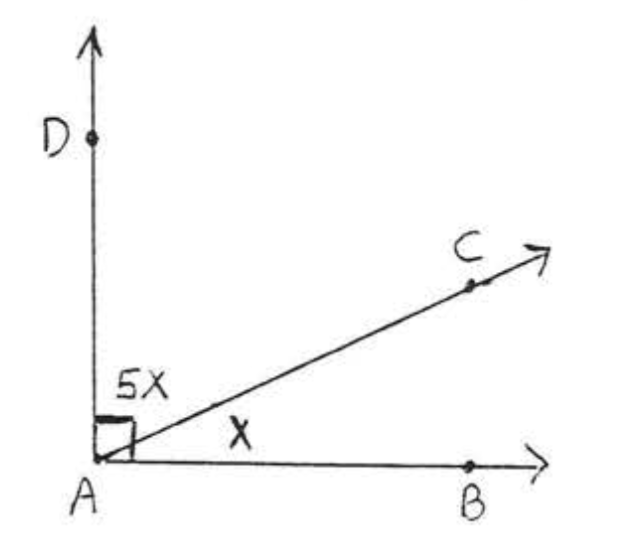
Знайдіть\(x\) і доповнюють кути:

Рішення
З тих пір\(\angle BAD = 90^{\circ}\),
\[\begin{array} {rcl} {x^2 + x} & {90^{\circ}} \\ {x^2 + x - 90} & {0} \\ {(x - 9)(x + 10)} & {0} \end{array}\]
\[\begin{array} {rcl} {x - 9} & = & {0} \\ {x} & = & {9} \end{array}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{array} {rcl} {x + 10} & = & {0} \\ {x} & = & {-10} \end{array}\]
\(\angle CAD = x = 90^{\circ}\). \(\angle CAD = x = -10^{\circ}.\)
\(\angle BAC = x^2 = 9^2 = 81^{\circ}\).
\(\angle BAC = \angle CAD = 81^{\circ} + 9^{\circ} = 90^{\circ}\).
Ми відхиляємо відповідь,\(x = -10\) оскільки міра кута завжди позитивна. (У тригонометрії при введенні спрямованих кутів кути можуть мати негативну міру. Однак у цій книзі всі кути будуть розглядатися як позитивні міри,)
Перевірка,\(x = 9\):

Відповідь:\(x = 9\),\(\angle CAD = 9^{\circ}\),\(\angle BAC = 81^{\circ}\).
Два кута називаються додатковими, якщо сума їх мір дорівнює\(180^{\circ}\). Кожен кут називається доповненням іншого. Наприклад, кут нахилу\(150^{\circ}\) і\(30^{\circ}\) є додатковими.

Знайдіть доповнення під кутом\(40^{\circ}\).
Рішення
\(180^{\circ} - 40^{\circ} = 140^{\circ}\).
Відповідь:\(140^{\circ}\).
Знайдіть\(x\) і додаткові кути:

Рішення
З тих пір\(\angle ADB = 180^{\circ}\),
\[\begin{array} {rcl} {4x - 20 + x} & = & {180^{\circ}} \\ {5x} & = & {180 + 20} \\ {5x} & = & {200} \\ {x} & = & {40} \end{array}\]
\(\angle ADC = 4x - 20 = 4(40) - 20 = 160 - 20 = 140^{\circ}\)
\(\angle BDC = x = 40^{\circ}\),
\(\angle ADC + \angle BDC = 140^{\circ} + 40^{\circ} = 180^{\circ}\).
Перевірка:

Відповідь
\(x = 40, \angle ADC = 140^{\circ}, \angle BDC = 40^{\circ}\).
Знайти\(x, y, z\):

Рішення
\(x^{\circ} = 180^{\circ} - 80^{\circ} = 100^{\circ}\)тому що\(x^{\circ}\) і\(80^{\circ}\) є мірами додаткових кутів.
\[\begin{array} {l} {y^{\circ} = 180^{\circ} - x^{\circ} = 180^{\circ} - 100^{\circ} = 80^{\circ}.} \\ {z^{\circ} = 180^{\circ} - 80^{\circ} = 100^{\circ}.} \end{array}\]
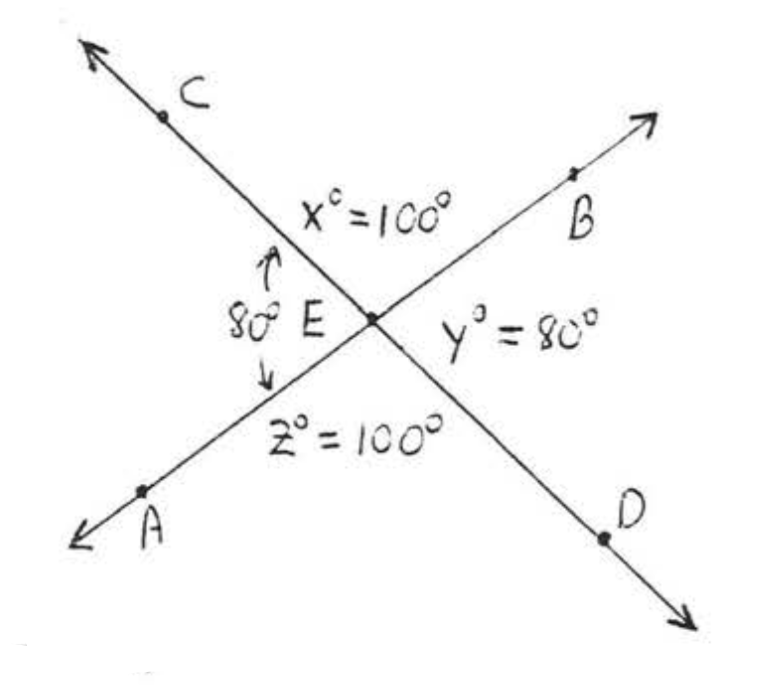
Відповідь:\(x = 100\),\(y = 80\),\(z = 100\).
Коли дві лінії перетинаються, як у прикладі E, вони утворюють дві пари кутів, які протилежні один одному називаються вертикальними кутами, На малюнку\(\PageIndex{7}\),\(\angle x\) і\(\angle x'\) є однією парою вертикальних кутів. \(\angle y\)і\(\angle y'\) a.re інша пара вертикальних кутів, Як запропонував приклад\(\PageIndex{5}\), \(\angle x = \angle x'\) and \(\angle y = \angle y'\). To see this in general, we can reason as follows: \(\angle x\) is the supplement of \(\angle y\) so \(\angle x = 180^{\circ} - \angle y\). \(\angle x'\) is also the supplement of \(\angle y\) so \(\angle x' = 180 - \angle y\). Therefore \(\angle x = \angle x'\). Similarly, we can show \(\angle y = \angle y'\). Therefore vertical angles are always equal.

Тепер ми можемо використовувати «вертикальні кути рівні» у вирішенні завдань:
Знайти\(x, y\), і\(z\):

Рішення
\(\angle x = 180^{\circ} - 80^{\circ} = 100^{\circ}\)тому що\(\angle x\) є доповненням\(80^{\circ}\).
\(\angle y = 80^{\circ}\)тому що вертикальні кути рівні.
\(\angle z = \angle x = 100^{\circ}\)тому що вертикальні кути рівні.
Відповідь:\(x = 100\),\(y = 80\),\(z = 100\).
Знайти\(x\):

Рішення
Так як вертикальні кути рівні,\(10x^2 = 40^{\circ}\).
\(\begin{array} {rclcrcl} {\text{Method 1:} \ \ \ \ \ \ 10x^2} & = & {40} & \ \ \ \ \ \ \ \ \ & {\text{Method 2:} \ \ \ \ \ \ 10x^2} & = & {40} \\ {10x^2 - 40} & = & {0} & \ \ \ \ \ \ \ \ \ & {\dfrac{10x^2}{10}} & = & {\dfrac{40}{10}} \\ {(10)(x^2 - 4)} & = & {0} & \ \ \ \ \ \ \ \ \ & {x^2} & = & {4} \\ {x^2 - 4} & = & {0} & \ \ \ \ \ \ \ \ \ & {x} & = & {\pm 2} \\ {(x + 2)(x - 2)} & = & {0} & \ \ \ \ \ \ \ \ \ & {} & & {} \end{array}\)
\(\begin{array} {rcl} {x + 2} & = & {0} \\ {x} & = & {-2} \end{array}\)\(\begin{array} {rcl} {x - 2} & = & {0} \\ {x} & = & {2} \end{array}\)
Якщо\(x = 2\) тоді\(\angle AEC = 10x^2 = 10(2)^2 = 10(4) = 40^{\circ}\).
Якщо\(x = -2\) тоді\(\angle AEC = 10x^2 = 10(-2)^2 = 10(4) = 40^{\circ}\).
Ми приймаємо рішення,\(x =-2\) хоча і\(x\) негативне, оскільки значення кута все\(10x^2\) ще позитивне.
Перевірка:

Відповідь:\(x = 2\) або\(x = -2\).
На схемі,\(AB\) являє собою дзеркало,\(CD\) являє собою промінь світла, що наближається до дзеркала з\(C\), і\(E\) являє собою око людини, яка спостерігає промінь, як він відбивається від дзеркала в\(D\). Відповідно до закону фізики\(\angle CDA\), званому кутом падіння, дорівнює\(\angle EDB\), називається кутом відбиття. Якщо\(\angle CDE = 60^{\circ}\), скільки дорівнює кут падіння?

Рішення
Нехай\(\x^{\circ} = \angle CDA = \angle EDB\).
\[\begin{array} {rcl} {x + x + 60} & = & {180} \\ {2x + 60} & = & {180} \\ {2x} & = & {120} \\ {x} & = & {60} \end{array}\]
Відповідь:\(60^{\circ}\)
Приклад теореми є твердженням «вертикальні кути завжди рівні». Теорема - це твердження, яке ми можемо довести, що це правда. Доказ - це процес міркування, який використовує твердження, які вже відомі як правдиві, щоб показати істинність нового твердження. Прикладом доказу є обговорення, що передує твердженню «вертикальні кути завжди рівні». Ми використовували факти про додаткові кути, які вже були відомі, щоб встановити нове твердження, що «вертикальні кути завжди рівні».
В ідеалі ми хотіли б довести всі твердження в математиці, які, на нашу думку, є правдивими. Однак, перш ніж ми зможемо почати доводити що-небудь, нам потрібні справжні твердження, з яких почати. Такі твердження повинні бути настільки самоочевидними, щоб не вимагати доказів самі. Твердження такого роду, яке ми вважаємо істинним без доказів, називається постулатом або аксіомою. Прикладом постулату є припущення, що всі кути можна виміряти в градусах. Це було використано, фактично не будучи заявленим у нашому доказі, що «вертикальні кути завжди рівні»,
Теореми, докази та постулати складають серце математики, і ми зіткнемося з багатьма іншими з них, продовжуючи вивчення геометрії.
Проблеми
1. Знайти доповнення під кутом
- \(37^{\circ}\)
- \(45^{\circ}\)
- \(53^{\circ}\)
- \(60^{\circ}\)
2. Знайти доповнення під кутом
- \(30^{\circ}\)
- \(40^{\circ}\)
- \(50^{\circ}\)
- \(81^{\circ}\)
3 - 6. Знайдіть\(x\) і доповнюють кути:
3.  4.
4. 
5.  6.
6. 
7. Знайдіть доповнення під кутом
- \(30^{\circ}\)
- \(37^{\circ}\)
- \(90^{\circ}\)
- \(120^{\circ}\)
8. Знайдіть доповнення під кутом
- \(45^{\circ}\)
- \(52^{\circ}\)
- \(85^{\circ}\)
- \(135^{\circ}\)
9 - 14. Знайдіть\(x\) і додаткові кути:
9. 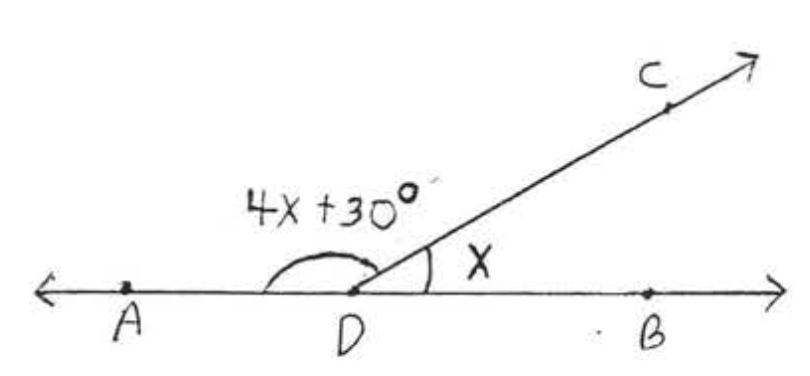 10.
10. 
11.  12.
12. 
13. 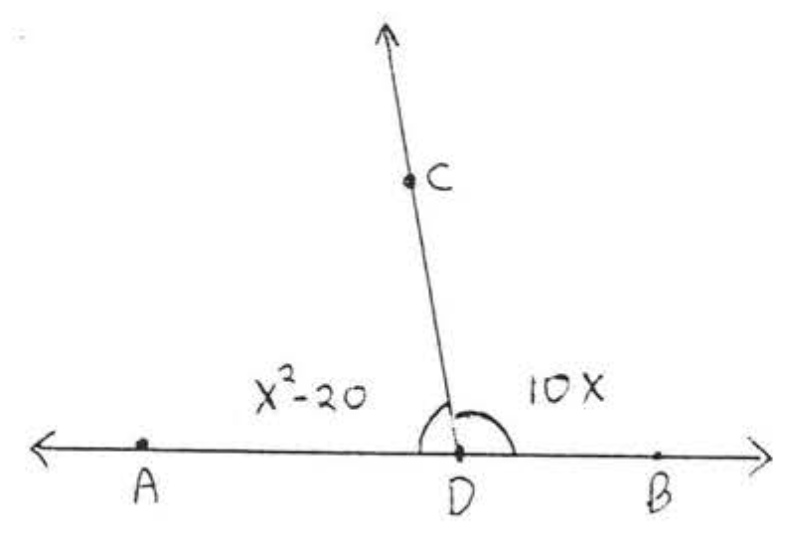 14.
14. 
15 - 22. Знайти\(x, y\), і\(z\):
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21.  22.
22. 
23 - 26. Знайти\(x\):
23.  24.
24. 
25.  26.
26. 
27. Знайти кут падіння,\(\angle CDA\):

28. Знайдіть,\(x\) чи дорівнює кут падіння\(40^{\circ}\):

