15.1: Проективне завершення

Last updated
Save as PDF

Page ID: 59161

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У евклідовій площині дві різні лінії можуть мати одну або нульову точку перетину (в останньому випадку лінії паралельні). Наша мета полягає в тому, щоб розширити евклідову площину ідеальними точками так, щоб будь-які дві різні лінії мали рівно одну точку перетину.

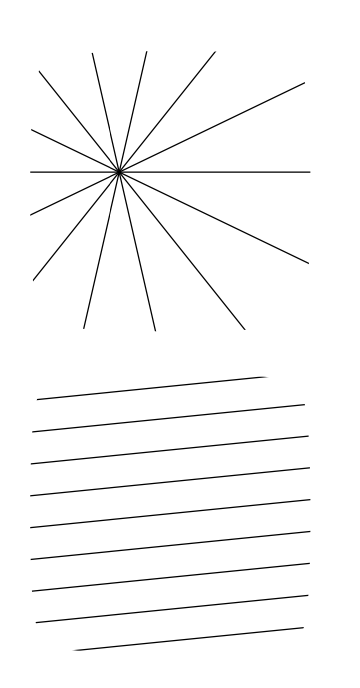
$2021-02-25 пнг$

Сукупність ліній в евклідовій площині називається одночасними, якщо всі вони перетинаються в одній точці або всі вони попарно паралельно. Максимальний набір одночасних ліній в площині називається олівцем. Є два типи олівців: центральні олівці містять всі лінії, що проходять через фіксовану точку, яка називається центром олівця, а паралельний олівець містить попарно паралельні лінії.

Кожна точка в евклідовій площині однозначно визначає центральний олівець з центром у ньому. Зверніть увагу, що будь-які дві лінії повністю визначають олівець, що містить обидва.

Додамо по одній ідеальній точці для кожного паралельного олівця, і припустимо, що всі ці ідеальні точки лежать на одній ідеальній лінії. Також припускаємо, що ідеальна лінія належить кожному паралельному олівцю.

Отримаємо так звану реальну проективну площину, або проективне завершення початкової площини. Він поставляється зі структурою падіння - ми говоримо, що три точки лежать на одному рядку, якщо відповідні олівці містять загальну лінію. Проективна геометрія вивчає цю структуру падінь.

Опишемо точки проективного завершення в координатах. Паралельний олівець містить ідеальну лінію і лінії$y = m \cdot x+b$ з фіксованим нахилом$m$; якщо$m=\infty$, ми припустимо, що лінії задаються рівняннями$x=a$. Тому реальна проективна площина містить кожну точку$(x,y)$ координатної площини плюс ідеальну лінію, яка містить одну ідеальну точку$P_m$ для кожного нахилу$m \in \mathbb{R} \cup \{\infty\}$.