15.7: Подвійність

Last updated
Save as PDF

Page ID: 59153

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Припустімо, що задано біекцію$P \leftrightarrow p$ між множиною ліній і множиною точок площини.

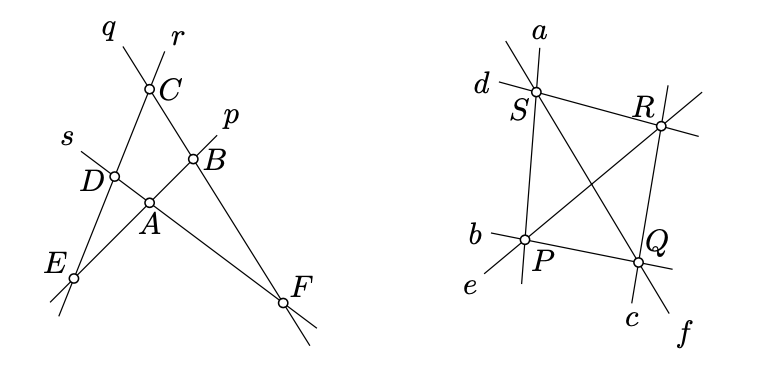
$2021-02-26 пнг$
Подвійні конфігурації

Тобто, задану точку$P$, позначаємо$p$ відповідною лінією; а навпаки, дану лінію$\ell$ позначаємо$L$ відповідною точкою.

Біджекція між точками та лініями називається подвійністю (Стандартне визначення подвійності є більш загальним; ми розглядаємо особливий випадок, який також називають полярністю.), якщо

$P\in \ell \ \ \ \Leftrightarrow \ \ \ p\ni L.$

для будь-якої точки$P$ і лінії$\ell$.

Вправа$\PageIndex{1}$

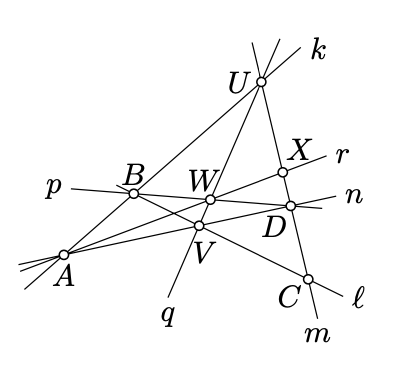
Розглянемо конфігурацію ліній і точок на схемі.

Почніть з загального чотирикутника$KLMN$ і розширте його на подвійну діаграму; позначте лінії і точки, використовуючи вищеописану угоду.

$2021-02-26 9.57.png$

Підказка: Малювати$a = (KN)$,$b = (KL)$,$c = (LM)$,$d = (MN)$, позначити$P = b \cap d$, і продовжувати.

Вправа$\PageIndex{2}$

Покажіть, що евклідова площина не допускає подвійності.

Підказка: Припустимо, що існує подвійність. Виберіть дві окремі паралельні лінії$\ell$ і$m$. Нехай$L$ і$M$ будуть їх подвійні точки. $s = (ML)$Поставте, тоді його подвійна точка$S$ повинна лежати на обох$\ell$ і$m$ - протиріччя.

Теорема$\PageIndex{1}$

Реальна проективна площина допускає подвійність.

Доказ

Розглянемо площину$\Pi$ і точку$O \not\in \Pi$ в просторі; припустимо, що$\hat{\Pi}$ позначає відповідну реальну проективну площину.

Нагадаємо, що$\Phi$ і$\Psi$ позначають сукупність всіх ліній і площин, що проходять через$O$. Згідно з спостереженням 15.3.1,$P\leftrightarrow\dot{P}$ між точками і між лініями$\hat{\Pi}$$\Phi$ і$\ell \leftrightarrow \dot{\ell}$ між ними існують двобічності в$\hat{\Pi}$ і$\Psi$ такі, що$P\in\ell$ якщо і тільки якщо$\dot{P} \subset \dot{\ell}$.

Залишилося побудувати біекцію$\dot{\ell} \leftrightarrow \dot{L}$ між$\Phi$ і$\Psi$ таким, що

\[\dot{P} \subset \dot{\ell} \ \ \ \iff \ \ \ \dot{p} \supset \dot{L}\]

для будь-яких двох ліній$\dot{P}$ і$\dot{L}$ проходження через$O$.

Встановити$\dot{\ell}$, щоб бути площиною через$O$, яка перпендикулярна до$\dot{L}$. Зверніть увагу, що обидві умови 15.7.1 еквівалентні$\dot{P} \perp \dot{L}$; отже, результат випливає.

Вправа$\PageIndex{3}$

Розглянемо евклідову площину з$(x,y)$ -координатами; припустимо, що$O$ позначає походження. Задану точку$P\ne O$ з координатами$(a,b)$ розглянемо пряму,$p$ задану рівнянням$a\cdot x+b\cdot y=1$.

Показати, що відповідність$P$ до$p$ поширюється на подвійність реальної проективної площини.

Який рядок відповідає$O$?

Яка точка відповідає прямій$a\cdot x +b\cdot y=0$?

Підказка

Припустимо,$M = (a, b)$ і лінія$s$ задана рівнянням$p \cdot x + q \cdot y = 1$. Тоді$M \in s$ еквівалентно$p \cdot a + q \cdot b = 1$.

Останнє еквівалентно$m \ni S$ де m - лінія, задана рівнянням$a \cdot x+b\ cdot y = 1$ і$S = (p, q)$.

Щоб розширити цей біекція на всю проективну площину, припустимо, що (1) ідеальна лінія відповідає початку і (2) ідеальна точка, задана олівцем ліній$b \cdot x−a \cdot y = c$ для різних значень c, відповідає прямій, заданій рівнянням$a \cdot x + b \cdot y =0$.

Подвійність говорить про те, що лінії і точки мають однакові права з точки зору захворюваності. Це дає можливість сформулювати еквівалентне подвійне твердження будь-якому твердженню в проективній геометрії. Наприклад, подвійний оператор для «точок$X$$Y$, і$Z$ лежати на одній лінії$\ell$" буде «лінії»$x$$y$, і$z$ перетинаються в одній точці $L$". Сформулюємо подвійне твердження для теореми Десарьє (теорема 15.6.1).

Теорема$\PageIndex{2}$ Dual Desargues' theorem

Розглянемо колінеарні точки$X$$Y$, і$Z$. Припустимо, що

Потім лінії$(AA')$$(BB')$, і$(CC')$ є одночасними.

У цій теоремі точки$X$$Y$, і$Z$ подвійні до ліній$(AA')$$(BB')$, і$(CC')$ в початковій формулюванні, і навпаки.

Як тільки теорема Десарьє доведена, застосовуючи дуальність (теорему$\PageIndex{1}$), ми отримуємо дуальну теорему Десарьє. Зауважте, що дуальна теорема Десарьє є зворотною до оригінальної теореми Десарьє (теорема 15.6.1).

Вправа$\PageIndex{4}$

Сформулюйте дуальну теорему Паппуса (див. Теорему 15.6.2).

Підказка

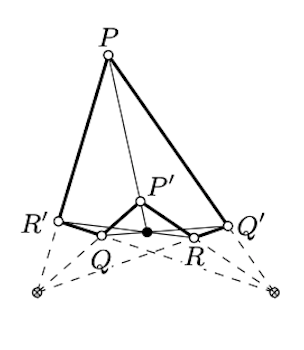
$2021-02-26 пнг$

Припустімо, що один набір одночасних рядків$a, b, c$, а інший набір$a', b', c'$ одночасних рядків задано. Набір

$\begin{array} {rclcrclcrcl} {P} & = & {b \cap c',} & \ \ \ \ & {Q} & = & {c \cap a',} & \ \ \ \ & {R} & = & {a \cap b',} \\ {P'} & = & {b' \cap c} & \ \ \ \ & {Q'} & = & {c' \cap a,} & \ \ \ \ & {R'} & = & {a' \cap b.} \end{array}$

Потім лінії$(PP')$$(QQ')$, і$(RR')$ є одночасними. (Це частковий випадок теореми Бріанкона.)

Вправа$\PageIndex{5}$

Вирішити наступну будівельну проблему

використання подвійної теореми Десарьє;
використовуючи теорему Паппуса або її подвійну.

Підказка

Припустимо$(AA')$ і$(BB')$ є заданими лініями і$C$ є заданою точкою. Застосуйте подвійну теорему Десарьє ($\PageIndex{2}$теорему) побудувати$C'$ так$(AA'), (BB')$, що і$(CC')$ є одночасними. З тих пір$(AA') \parallel (BB')$, ми отримуємо, що$(AA') \parallel (BB') \parallel (CC')$.

Тепер припустимо, що$P$ це задана точка і$(R'Q)$,$(P'R)$ є задані паралельні лінії. Спробуйте побудувати точку,$Q'$ як у дуальній теоремі Паппа (див. Розв'язок вправи$\PageIndex{4}$).

Проблема$\PageIndex{1}$

За двома паралельними лініями побудуйте третю паралельну лінію через задану точку лише лінійкою.

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Теорема\(\PageIndex{1}\)

Вправа\(\PageIndex{3}\)

Теорема\(\PageIndex{2}\) Dual Desargues' theorem

Вправа\(\PageIndex{4}\)

Вправа\(\PageIndex{5}\)

Проблема\(\PageIndex{1}\)