15.8: Будівництво полярного

Last updated
Save as PDF

Page ID: 59152

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

У цьому розділі ми опишемо потужний трюк, який можна використовувати в конструкціях з лінійкою.

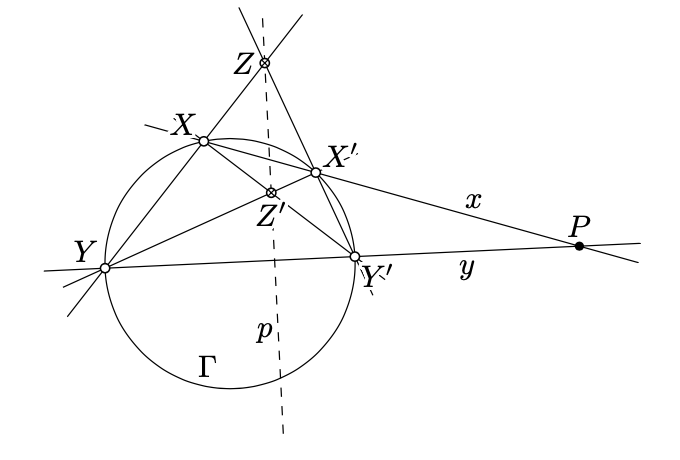
$2021-02-26 пнг$

Припустимо,$\Gamma$ це коло в площині$P\notin \Gamma$ і.Draw дві лінії$x$ і$y$ через$P$ які перетинаються$\Gamma$ в двох парах точок$X$,$X'$ і $Y$,$Y'$. Нехай$Z=(XY) \cap (X'Y')$ і$Z'=(XY') \cap(X'Y)$. Розглянемо лінію$p=(ZZ')$.

Претензія$\PageIndex{1}$

Побудована лінія$p=(ZZ')$ не залежить від вибору ліній$x$ і$y$.

Більш того,$P \leftrightarrow p$ може бути розширена до подвійності така, що будь-яка точка$P$ на колі$\Gamma$ відповідає прямій$p$ дотичній до$\Gamma$ at$P$.

Ми будемо використовувати цю претензію без доказів, але доказ не є важким. Якщо$P$ лежить зовні$\Gamma$, це можна зробити, рухаючись$P$ до нескінченності, зберігаючи$\Gamma$ фіксований як набір. Якщо$P$ лежить всередині$\Gamma$, це можна зробити, рухаючись$P$ до центру$\Gamma$. Існування відповідних проективних перетворень випливає з ідеї у вправі 16.3.1.

Лінія$p$ називається полярної точки$P$ по відношенню до$\Gamma$.

Точка$P$ називається $p$полюсом прямої щодо$\Gamma$.

Вправа$\PageIndex{1}$

Поверніть описану конструкцію. Тобто, задавши коло$\Gamma$ і пряму,$p$ яка не є дотичною$\Gamma$, побудувати$P$ таку точку, щоб описувана конструкція для$P$ і$\Gamma$ виробляла пряму$p$.

Підказка: Припустимо$p = (QR)$; позначають$q$ і$r$ подвійні лінії, вироблені конструкцією. Тоді, за$P$ претензією$\PageIndex{1}$, є точкою перетину$q$ і$r$.

Вправа$\PageIndex{2}$

$p$Дозволяти бути полярною$P$ лінією точки по відношенню до кола$\Gamma$. Припустимо, що$p$ перетинається$\Gamma$ в точках$V$ і$W$. Покажіть, що лінії$(PV)$ і$(PW)$ дотичні до$\Gamma$.

Придумайте лише лінійку побудови дотичних ліній до заданого кола$\Gamma$ через задану точку$P\not\in \Gamma$.

Підказка: Лінія$v$ полярна до$V$ дотична до$\Gamma$. Оскільки$V \in p$, за$\PageIndex{1}$ претензією, ми отримуємо, що$P \in v$; тобто$(PV) = v$. Звідси випливає твердження.

Вправа$\PageIndex{3}$

Припустимо дві концентричні кола$\Gamma$ і$\Gamma'$ задані. Побудуйте загальний центр$\Gamma$ і лише за$\Gamma'$ допомогою лінійки.

Підказка

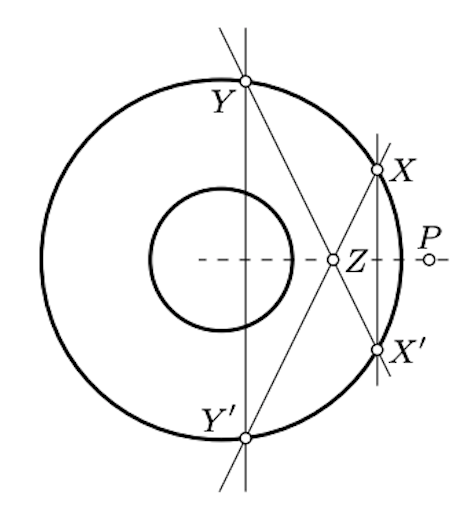
$2021-02-26 пнг$

Виберіть точку$P$ поза більшим колом. Побудувати лінії подвійні$P$ для обох кіл. Зверніть увагу, що ці дві лінії паралельні.

Припустимо, що лінії перетинають більшу окружність в двох парах точок$X, X'$ і$Y, Y'$. Набір$Z = (XY) \cap (X'Y')$. Зверніть увагу, що лінія$(PZ)$ проходить через загальний центр.

Центр - це перетин$(PZ)$ і інша лінія побудована таким же чином.

Вправа$\PageIndex{4}$

Припустимо, що задано лінію$\ell$ і коло$\Gamma$ з її центром$O$. Припустимо$O\notin \ell$. Побудуйте перпендикуляр тільки$\ell$ з лінійкою.$O$

Підказка: Побудувати полярні лінії до двох точок на$\ell$. $L$Позначте шляхом перетину цих двох ліній. Зверніть увагу, що$\ell$ є полярним до$L$ і тому$(OL) \perp \ell$.

Претензія\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)

Вправа\(\PageIndex{4}\)