7.4: Кути трикутників

Last updated
Save as PDF

Page ID: 59051

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Теорема$\PageIndex{1}$

У будь-якому$\triangle ABC$, у нас є

$\measuredangle ABC + \measuredangle BCA + \measuredangle CAB \equiv \pi.$

Доказ

Спочатку зауважте,$\triangle ABC$ що якщо вироджений, то рівність випливає з Слідство 2.4.1. Далі припускаємо, що$\triangle ABC$ є невиродженим.

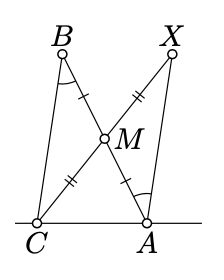
$2021-02-09 пнг$

$X$Дозволяти відображенням$C$ через середину$M$$[AB]$. За пропозицією 7.2.1$\measuredangle BAX = \measuredangle ABC$. Зверніть увагу, що$(AX)$ це відображення$(CB)$ поперек$M$; отже, теорема 7.2.1,$(AX) \parallel (CB)$.

Так як$[BM]$ і$[MX]$ не перетинаються$(CA)$$B, M$, точки і$X$ лежать на одній стороні$(CA)$. Застосовуючи поперечну властивість для поперечного$(CA)$ до$(AX)$ і$(CB)$, ми отримуємо, що

\[\measuredangle BCA + \measuredangle CAX \equiv \pi.\]

З тих пір$\measuredangle BAX = \measuredangle ABC$, у нас є

$\measuredangle CAX \equiv \measuredangle CAB + \measuredangle ABC$

Остання ідентичність і 7.4.1 мають на увазі теорему.

Вправа$\PageIndex{1}$

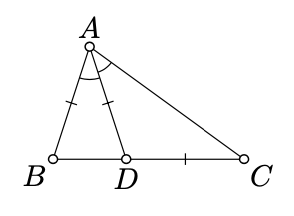
$2021-02-09 пнг$

$\triangle ABC$Дозволяти бути невиродженим трикутником. Припустимо, є$D \in [BC]$ такий момент, що

$\measuredangle BAD \equiv \measuredangle DAC, BA = AD = DC.$

Знайдіть кути$\triangle ABC$.

Підказка: Застосовуйте двічі теорему 4.3.1 і двічі теорему$\PageIndex{1}$.

Вправа$\PageIndex{2}$

Покажіть, що

$|\measuredangle ABC| + |\measuredangle BCA| + |\measuredangle CAB| = \pi$

для будь-якого$\triangle ABC$.

Підказка

Якщо$\triangle ABC$ вироджений, то одна з вимірювань кута дорівнює,$\pi$ а дві інші - 0. Звідси і результат.

Припустімо$\triangle ABC$, що є невиродженим. Набір$\alpha = \measuredangle CAB$,$\beta = \measuredangle ABC$, і$\gamma = \measuredangle BCA$.

За теоремою 3.3.1, можна припустити, що$0 < \alpha, \beta, \gamma < \pi$. Тому,

\[0 > \alpha + \beta + \gamma < 3 \cdot \pi.\]

За$\Pageindex{1}$ теоремою

\[\alpha + \beta +\gamma \equiv \pi.\]

З 7.4.2 і 7.4.3 випливає результат.

Вправа$\PageIndex{3}$

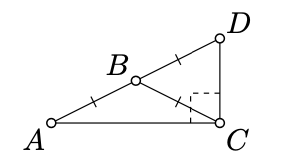
$\triangle ABC$Дозволяти бути ізоселевий невироджений трикутник з основою$[AC]$. Припустимо,$D$ це відображення$A$ поперек$B$. Покажіть,$\angle ACD$ що правильно.

$2021-02-09 пнг$

Підказка: Застосовуйте двічі теорему 4.3.1 і двічі теорему$\PageIndex{1}$.

Вправа$\PageIndex{4}$

$\triangle ABC$Дозволяти рівнобедрений невироджений трикутник з основою$[AC]$. Припустімо, що коло проходить через$A$, по центру в точці на$[AB]$, і$(BC)$ дотичною до точки$X$. Покажіть, що$\measuredangle CAX = \pm \dfrac{\pi}{4}$.

Підказка

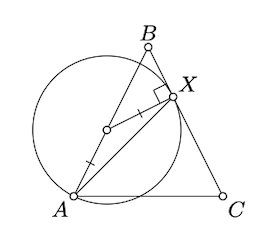
$2021-02-09 пн$

Припустимо, що$O$ позначає центр кола.

Зверніть увагу, що$\triangle AOX$ є рівнобедреним і$\angle OXC$ є правильним. Застосовуючи теорему$\PageIndex{1}$ і теорему 4.3.1 і спрощуючи, ми повинні отримати$4 \cdot \measuredangle CAX \equiv \pi$.

Покажіть, що$\angle CAX$ має бути гострим. Звідси випливає, що$\measuredangle CAX = \pm \dfrac{\pi}{4}$.

Вправа$\PageIndex{5}$

Покажіть, що для будь-якого чотирикутника$ABCD$ ми маємо

$\measuredangle ABC + \measuredangle BCD + \measuredangle CDA + \measuredangle DAB \equiv 0$.

Підказка: Застосувати теорему$\PageIndex{1}$ до$\triangle ABC$ і$\triangle BDA$.

Теорема\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)

Вправа\(\PageIndex{4}\)

Вправа\(\PageIndex{5}\)