7.1: Паралельні лінії

Last updated
Save as PDF

Page ID: 59042

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

$2021-02-09 пнг$

Внаслідок Аксіоми II будь-які дві різні лінії$\ell$ і$m$ мають або одну спільну точку, або жодної. У першому випадку вони перетинаються (коротко$\ell \nparallel m$); у другому випадку l і m кажуть, що паралельні (коротко,$\ell \parallel m$); крім того, лінія завжди розглядається як паралельна собі.

Щоб підкреслити, що дві лінії на схемі паралельні, відзначимо їх стрілками одного типу.

Пропозиція$\PageIndex{1}$

Дозволяти$\ell, m$, і$n$ бути три рядки. Припустимо, що$n \perp m$ і$m \perp \ell$. Потім$\ell \parallel n$.

Доказ: Припустимо, навпаки; тобто,$\ell \nparallel m$. Тоді є точка, скажімо$Z$, перетину$\ell$ і$n$. Потім за теоремою 5.3.1,$\ell = n$. Оскільки будь-яка лінія паралельна собі, ми маємо це$\ell \parallel n$ — протиріччя.

Теорема$\PageIndex{1}$

Для будь-якої точки$P$ і будь-якої лінії$\ell$ існує унікальна лінія$m$, яка проходить через$P$ і паралельна$\ell$.

Вищевказана теорема має дві частини, існування та єдиність. На доказ унікальності будемо використовувати метод подібних трикутників.

Доказ

Застосовуйте теорему 5.3.1 два рази, спочатку побудуйте$n$ пряму,$P$ яка перпендикулярна$\ell$, а по-друге, щоб побудувати лінію$n$ через$P$ перпендикулярну$m$. Потім застосуйте Пропозицію$\PageIndex{1}$.

Унікальність. Якщо$P \in \ell$, то$m =\ell$ за визначенням паралельних ліній. Далі припускаємо$P \not\in \ell$.

Побудуємо лінії$n \ni P$ і$m \ni P$ як на доказі існування, так$m \parallel \ell$.

Припустимо, що є ще одна лінія$s \ni P$ паралельно$\ell$. Виберіть точку$Q \in s$, яка$\ell$ лежить з тієї ж сторони від$m$. $R$Дозволяти бути точкою стопи$Q$ на$n$.

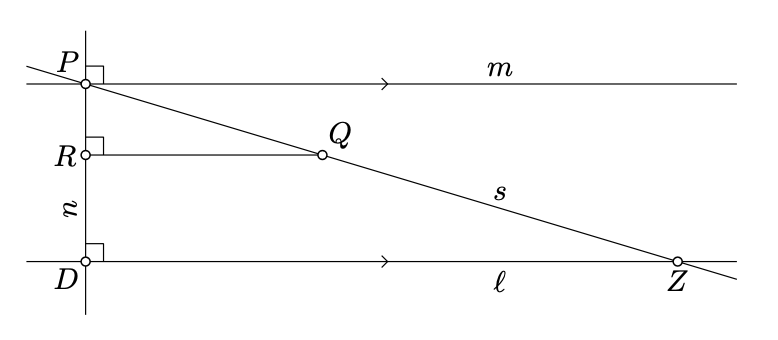
$2021-02-09 пнг$

$D$Дозволяти точка перетину$n$ і$\ell$. Згідно з пропозицією$\PageIndex{1}$$(QR) \parallel m$. Тому$Q, R$, і$\ell$ ляжте на одну сторону$m$. Зокрема,$R \in [PD)$.

Вибирайте$Z \in [PQ)$ такі, що

$\dfrac{PZ}{PQ} = \dfrac{PD}{PR}.$

За умовою подібності SAS (або еквівалентно аксіомою V) ми маємо це$\triangle RPQ \sim \triangle DPZ$; отже$(ZD) \perp (PD)$. Звідси випливає, що$Z$ лежить на$\ell$ і$s$ - умові.

Слідство$\PageIndex{2}$

Припустимо$\ell, m$, і$n$ є рядки такі, що$\ell \parallel m$ і$m \parallel n$. Потім$\ell \parallel n$.

Доказ: Припустимо, навпаки; тобто,$\ell \nparallel n$. Тоді є сенс$P \in \ell \cap n$. За теоремою$\PageIndex{1}$,$n = \ell$ — протиріччя.

Зверніть увагу, що з визначення ми маємо, що$\ell \parallel m$ якщо і тільки якщо$m \parallel \ell$. Тому, згідно з вищенаведеним наслідком,$\parallel$ "" - це відношення еквівалентності. Тобто для будь-яких ліній$\ell, m$ і$n$ дотримуються такі умови:

(i)$\ell \parallel \ell$;
(ii) якщо$\ell \parallel m$, то$m \parallel \ell$;
(iii) якщо$\ell \parallel m$ і$m \parallel n$, то$\ell \parallel n$.

Вправа$\PageIndex{1}$

Нехай$k, \ell, m$, і$n$ бути лінії такі$k \perp \ell$, що$\ell \perp m$, і$m \perp n$. Покажіть, що$k \nparallel n$.

Підказка: Застосуйте пропозицію$\PageIndex{1}$, щоб показати це$k \parallel m$. За наслідком$\PageIndex{2}$,$k \parallel n \Rightarrow m \parallel n$. Останнє суперечить цьому$m \perp n$.

Вправа$\PageIndex{1}$

Зробіть лінійку і компас побудови лінії через задану точку, яка паралельна заданій лінії.

Підказка: Повторіть конструкцію у вправі 5.7.1 двічі.

Пропозиція\(\PageIndex{1}\)

Теорема\(\PageIndex{1}\)

Слідство\(\PageIndex{2}\)

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{1}\)