7.6: Метод координат

Last updated
Save as PDF

Page ID: 59035

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Наступна вправа є важливою; вона показує, що наше аксіоматичне визначення узгоджується з визначенням моделі.

Вправа$\PageIndex{1}$

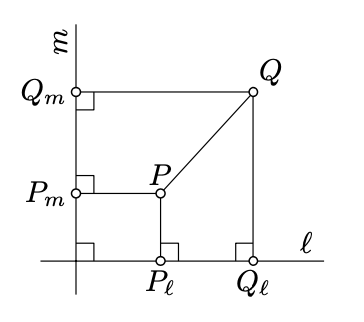
$2021-02-11 пн$

$m$Дозволяти$\ell$ і бути перпендикулярними лініями в евклідовій площині. З огляду на точку$P$, нехай$P_{\ell}$ і$P_m$ позначають точки стопи$P$ на$\ell$ і$m$ відповідно.

Покажіть, що для будь-якого$X \in \ell$ і$Y \in m$ є унікальний момент$P$ такий, що$P_{\ell} = X$ і$P_m = Y$.
Покажіть, що$PQ^2 = P_{\ell}Q_{\ell}^2 + P_m Q_m^2$ для будь-якої пари очок$P$ і$Q$.
Зробіть висновок, що площина ізометрична до$(\mathbb{R}^2, d_2)$.

Підказка

(а). Використовуйте єдиність паралельної прямої (Теорема 7.1.1).

(б). Використовуйте лему 7.5.1 та теорему Піфагора (Теорема 6.2.1)

Після того, як ця вправа буде вирішена, ми можемо застосувати метод координат для вирішення будь-якої задачі в геометрії евклідової площини. Цей метод є потужним і універсальним; він буде розвиватися далі в главі 18.

Вправа$\PageIndex{2}$

Використовуйте Вправу,$\PageIndex{1}$ щоб дати альтернативний доказ теореми 3.5.1 в евклідовій площині.

Тобто довести, що дані дійсні числа$a, b$, і$c$ такі, що

$0 < a \le b \le c \le a + b$,

є трикутник$ABC$ такий$a = BC$, що$b = CA$, і$c = AB$.

Підказка

Набір$A = (0, 0), B = (c, 0)$, і$C = (x, y)$. Зрозуміло$AB = c$,$AC^2 = x^2 + y^2$ і$BC^2 = (c - x)^2 + y^2$.

Залишається показати, що існує пара дійсних чисел$(x, y)$, які задовольняють наступній системі рівнянь:

$\begin{cases} b^2 = x^2 + y^2 \\ a^2 = (c- x)^2 + y^2 \end{cases}$

якщо$0 < a \le b \le c \le a + c$.

Вправа$\PageIndex{3}$

Розглянемо дві різні точки$A = (x_A, y_A)$ і$B = (x_B, y_B)$ на координатній площині. Показати, що перпендикулярна бісектриса до$[AB]$ описується рівнянням

$2 \cdot (x_B - x_A) \cdot x + 2 \cdot (y_B - y_A) \cdot y = x_B^2 + y_B^2 - x_A^2 - y_B^2$.

Зробіть висновок, що лінія може бути визначена як підмножина координатної площини наступного типу:

Розв'язки рівняння$a \cdot x + b \cdot y = c$ для деяких констант$a, b$, і$c$ таких, що$a \ne 0$ або$b \ne 0$.
Безліч точок$(a \cdot t + c, b \cdot t + d)$ для деяких констант$a, b, c$, і$d$ таких, що$a \ne 0$ або$b \ne 0$ і все$t \in \mathbb{R}$.

Підказка

Зверніть увагу, що$MA = MB$ якщо і тільки якщо

$(x - x_A)^2 + (y - y_A)^2 = (x - x_B)^2 + (y - y_B)^2$

де$M = (x, y)$. Щоб довести першу частину, спростіть це рівняння. Для інших частин використовуйте, щоб будь-яка лінія була перпендикулярною бісектрисою до деякого відрізка лінії.

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)