Skip to main content
LibreTexts - Ukrayinska

7.5: Паралелограми

  1. Last updated
  2. Save as PDF
  • Page ID
    59034

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

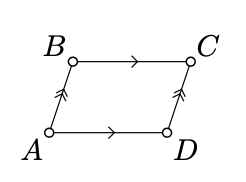
    2021-02-11 пнг

    Чотирикутник\(ABCD\) в евклідовій площині називається невиродженим, якщо на одній прямій не\(A, B, C, D\) лежать три точки.

    Невироджений чотирикутник називається паралелограмом, якщо його протилежні сторони паралельні.

    Лемма\(\PageIndex{1}\)

    Будь-який паралелограм центрально симетричний відносно середини однієї з його діагоналей.

    Зокрема, якщо\(\square ABCD\) це паралелограм, то

    (а) його діагоналі\([AC]\) і\([BD]\) перетинаються один з одним в їх середніх точках;

    (б)\(\measuredangle ABC = \measuredangle CDA\);

    (c)\(AB = CD\).

    Доказ

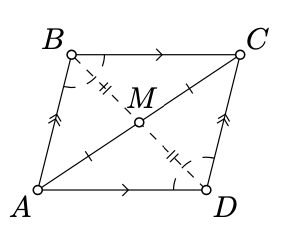
    2021-02-11 пнг

    \(\square ABCD\)Дозволяти бути паралелограм. \(M\)Позначають середньою точкою\([AC]\).

    Оскільки\((AB)\parallel (CD)\), Теорема 7.2.1 передбачає, що\((CD)\) це відображення\((AB)\) поперек\(M\). Таким же чином\((BC)\) відбувається відображення\((DA)\) поперек\(M\). Оскільки\(\square ABCD\) є невиродженим, то випливає, що\(D\) є відображенням\(B\) поперек\(M\); іншими словами,\(M\) це середина\([BD]\).

    Решта тверджень слідують, оскільки відображення поперек\(M\) є прямим рухом площини (див. Пропозиція 7.2.1).

    Вправа\(\PageIndex{1}\)

    Припустимо,\(ABCD\) це чотирикутник такий, що

    \(AB = CD = BC = DA.\)

    Такий, що\(ABCD\) є паралелограмом.

    Підказка

    Так\(\triangle ABC\) як рівнобедрений,\(\measuredangle CAB = \measuredangle BCA\).

    За ССС,\(\triangle ABC \cong \triangle CDA\). Тому,\(\pm \measuredangle DCA = \measuredangle BCA = \measuredangle CAB\).

    Так як\(D \ne C\), отримуємо «-» в останній формулі. Використовуйте поперечну властивість (теорема 7.3.1), щоб показати це\((AB) \parallel (CD)\). Повторіть аргумент, щоб показати це\((AD) \parallel (BC)\).

    Чотирикутник, як у вправі вище, називається ромбом.

    Чотирикутник ABCD називається прямокутником, якщо кути ABC, BCD, CDA та DAB мають рацію. Зверніть увагу, що згідно поперечному властивості (теорема 7.3.1) будь-який прямокутник є паралелограмом.

    Прямокутник з рівними сторонами називається квадратом.

    Вправа\(\PageIndex{2}\)

    Показати, що паралелограм\(ABCD\) є прямокутником, якщо і тільки якщо\(AC = BD\).

    Підказка

    За Лемма\(\PageIndex{1}\) і ССС,\(AC = BD\) якщо і тільки якщо\(\angle ABC = \pm \measuredangle BCD\). За поперечною властивістю (Теорема 7.3.1),\(\measuredangle ABC + \measuredangle BCD \equiv \pi\).

    Тому\(AC = BD\) якщо і тільки якщо\(\measuredangle ABC = \measuredangle BCD = \pm \dfrac{\pi}{2}\).

    Вправа\(\PageIndex{3}\)

    Показати, що паралелограм\(ABCD\) є ромбом тоді і тільки якщо\((AC) \perp (BD)\).

    Підказка

    Закріпіть паралелограм\(ABCD\). За лемою\(\PageIndex{1}\), його діагоналі\([AC]\) і\([BD]\) мають загальну середину; позначають її по\(M\).

    Використовуйте SSS та Lemma\(\PageIndex{1}\), щоб показати, що

    \(AB = CD \Leftrightarrow \triangle AMB \cong \triangle AMD \Leftrightarrow \measuredangle AMB = \pm \dfrac{\pi}{2}.\)

    Припустимо\(\ell \parallel m\), і\(X, Y \in m\). Нехай\(X'\) і\(Y'\) позначають точки стопи\(X\) і\(Y\) далі\(\ell\). Зверніть увагу, що\(\square XYY'X'\) це прямокутник. Лемма\(\PageIndex{1}\),\(XX' = YY'\). Тобто будь-яка точка на\(m\) лежить на однаковій відстані від\(\ell\). Ця відстань називається відстанню між\(\ell\) і\(m\).