7.3: Поперечна властивість

Last updated
Save as PDF

Page ID: 59060

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

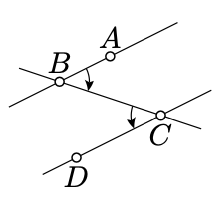
Якщо лінія$t$ перетинає кожну пряму$\ell$ і$m$ в одній точці, то ми говоримо, що$t$ є поперечним до$\ell$ і$m$. Наприклад, на схемі лінія ($CB$) - поперечна до ($AB$) і ($CD$).

$2021-02-09 пнг$

Теорема$\PageIndex{1}$: Transversal Property

$(AB) \parallel (CD)$якщо і тільки якщо

\[2 \cdot (\measuredangle ABC + \measuredangle BCD) \equiv 0. \nonumber\]

Аналогічно

$\measuredangle ABC + \measuredangle BCD \equiv 0$або$\measuredangle ABC + \measuredangle BCD \equiv \pi.$

Причому якщо$(AB) \ne (CD)$, то в першому випадку$A$ і$D$ лежать на протилежні сторони$(BC)$; у другому випадку$A$ і$D$ лежати на тих же сторонам$(BC)$.

Доказ

Частина «тільки якщо». $O$Позначають середньою точкою$[BC]$.

Припустимо$(AB) \parallel (CD)$. Відповідно до теореми 7.2.1,$(CD)$ є відображенням$(AB)$ поперек$O$.

Нехай$A'$ буде відображенням$A$ поперек$O$. Тоді$A' \in (CD)$ і за пропозицією 7.2.1 ми маємо це

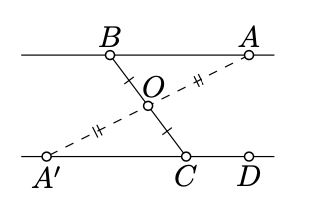
$2021-02-09 пн$

\[\measuredangle ABO = \measuredangle A'CO.\]

Зверніть увагу, що

\[\measuredangle ABO \equiv \measuredangle ABC, \ \ \ \ \measuredangle A'CO \equiv \measuredangle BCA'.\]

Так як$A', C$ і$D$ лежати на одній лінії, Вправа 2.4.2 має на увазі, що

\[2 \cdot \measuredangle BCD \equiv 2 \cdot \measuredangle BCA'.\]

Нарешті, зауважте, що 7.3.2, 7.3.3 та 7.3.4 означають 7.3.1.

«Якщо» -частина. За теоремою 7.2.1 існує унікальна лінія$(CD)$ через$C$, яка паралельна$(AB)$. З частини «тільки якщо» ми знаємо, що 7.3.1 тримає.

З іншого боку, є унікальна лінія$(CD)$ така, що 7.3.1 тримає. Дійсно, припустимо, є дві такі лінії$(CD)$ і$(CD')$, то

$2 \cdot (\measuredangle ABC + \measuredangle BCD) \equiv 2 \cdot (\measuredangle ABC + \measuredangle BCD') \equiv 0$.

Тому$2 \cdot \measuredangle BCD \equiv 2 \cdot BCD'$ і за допомогою вправи 2.4.2$D' \in (CD)$, або еквівалентно лінія$(CD)$ збігається з$(CD')$.

Тому якщо 7.3.1 тримає, то$(CD) \parallel (AB)$.

Нарешті, якщо$(AB) \ne (CD)$$A$ і$D$ лежати на протилежних сторонам$(BC)$, то$\angle ABC$ і$\angle BCD$ мають протилежні ознаки. Тому

$-\pi < \measuredangle ABC + \measuredangle BCD < \pi.$

Застосовуючи 7.3.1, отримуємо$\measuredangle ABC + \measuredangle BCD = 0$.

Аналогічно якщо$A$ і$D$ лежати на одній стороні$(BC)$, то$\angle ABC$ і$\angle BCD$ мають такий же знак. Тому

$0 < |\measuredangle ABC + \measuredangle BCD| < 2\cdot \pi$

і 7.3.1 означає, що$\measurdangle ABC + \measuredangle BCD \equiv \pi$.

Вправа$\PageIndex{1}$

$\triangle ABC$Дозволяти бути невиродженим трикутником, і$P$ лежить між$A$ і$B$. Припустимо, що лінія$\ell$ проходить через$P$ і паралельна$(AC)$. Покажіть, що$\ell$ перетинає сторону$[BC]$ в іншій точці, скажімо$Q$, і

$\triangle ABC \sim \triangle PBQ.$

Зокрема,

$\dfrac{PB}{AB} = \dfrac{QB}{CB}.$

Підказка

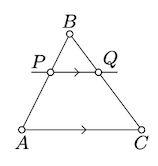
$2021-02-09 пнг$

Оскільки$\ell \parallel (AC)$ вона не може перетинатися$[AC]$. За теоремою Паша (теорема 3.4.1),$\ell$ повинен перетнути іншу сторону$\triangle ABC$. Тому$\ell$ хрест$[BC]$; позначимо точку перетину по$Q$.

Використовуйте поперечну властивість (Теорема$\PageIndex{1}$), щоб показати це$\measuredangle BAC = \measuredangle BPQ$. Цей же аргумент показує, що$\measuredangel ACB = \measuredangle PQB$; залишається застосувати умову подібності АА.

Вправа$\PageIndex{2}$

Трисекти заданий відрізок за допомогою лінійки і циркуля.

Відповідь: Припустимо, нам потрібно перетнути відрізок$[AB]$. Побудувати лінію$\ell \ne (AB)$ з чотирма точками$A, C_1, C_2, C_3$ такі, що$C_1$ і$C_2$ трисекти$[AC_3]$. Намалюйте лінію$(BC_3)$ і проведіть паралельні лінії через$C_1$ і$C_2$. Точки перетину цих двох ліній з$(AB)$ перетинають відрізок$[AB]$.

Теорема\(\PageIndex{1}\): Transversal Property

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)