7.7: Аполлонське коло

Last updated
Save as PDF

Page ID: 59041

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Вправи в цьому розділі наведені як ілюстрації до методу координат — він не буде використовуватися далі в продовженні.

Вправа$\PageIndex{1}$

Показати, що для фіксованих дійсних значень$a$$b$, і$c$ рівняння

$x^2 + y^2 + a \cdot x + b \cdot y + c = 0$

описує коло, одноточкову множину або порожню множину.

Показати, що якщо це коло, то він має центр$(- \dfrac{a}{2}, -\dfrac{b}{2})$ і радіус$r = \dfrac{1}{2} \cdot \sqrt{a^2 + b^2 - 4 \cdot c}$.

Підказка

Перепишіть його наступним чином і подумайте

$(x + \dfrac{a}{2})^2 + (y + \dfrac{b}{2})^2 = (\dfrac{a}{2})^2 + (\dfrac{b}{2})^2 - c$.

Вправа$\PageIndex{2}$

Скористайтеся попередньою вправою, щоб показати, що задано дві різні точки$A$$B$ та додатне дійсне число$k \ne 1$, місце$M$ розташування точок,$AM = k \cdot BM$ таких як коло.

$2021-02-15 пнг$

Підказка

Ми можемо вибрати координати так, що$B = (0, 0)$ і$A = (a, 0)$ для деяких$a > 0$. Якщо$M = (x, y)$, то рівняння$AM = k \cdot BM$ можна записати в координатах як

$k^2 \cdot (x^2 + y^2) = (x - a)^2 + y^2.$

Залишилося переписати це рівняння як у Вправі$\PageIndex{1}$.

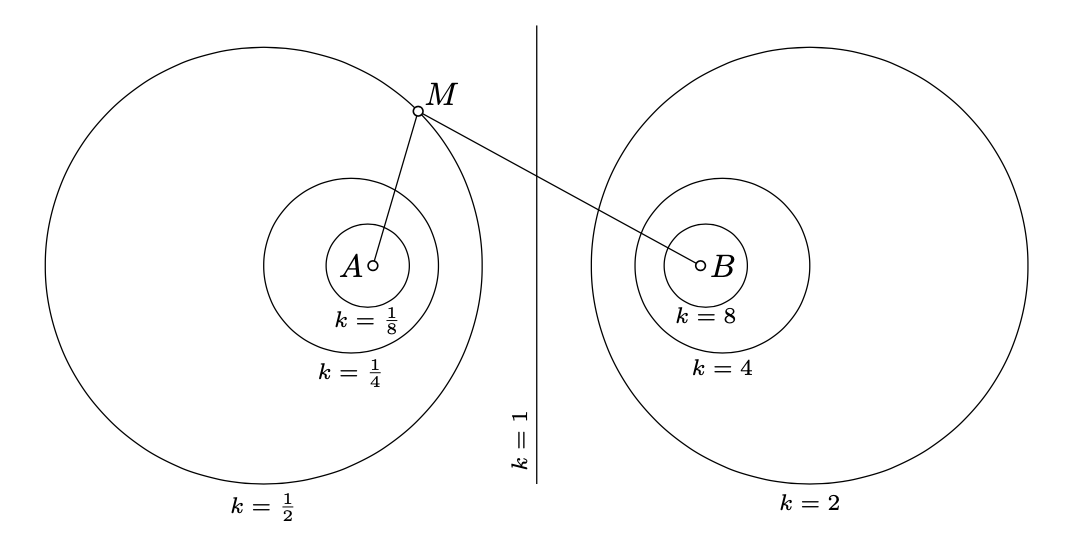
Коло у вправі вище - приклад так званого аполлонського кола з фокусами$A$ і$B$. Мало хто з цих кіл для різних значень$k$ показані на діаграмі; бо$k = 1$, вона стає перпендикулярною бісектрисою до$[AB]$.

Вправа$\PageIndex{3}$

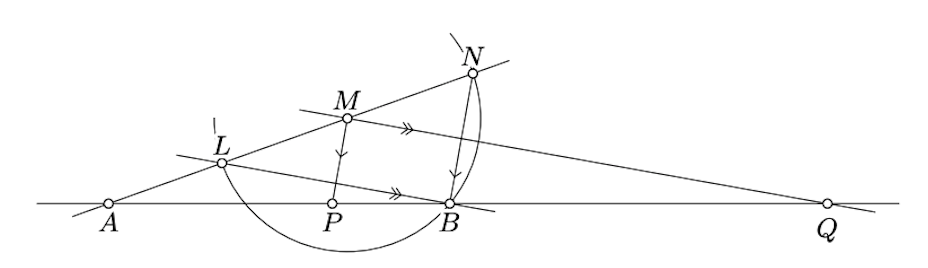
Зробіть лінійку і компас побудови аполлонського кола з заданими$A$ фокусами і$B$ через задану точку$M$.

Підказка

Припустимо$M \not\in (AB)$. Покажіть і використовуйте, що точки$P$ і$Q$ побудовані на наступній схемі лежать на аполлонівському колі.

$2021-02-15 пнг$

Вправа\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)