2.5: Вертикальні кути

Last updated
Save as PDF

Page ID: 59137

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

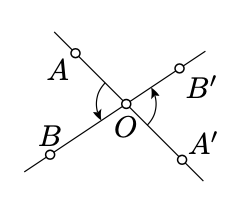
Пара кутів$AOB$ і$A'OB'$ називається вертикальною, якщо точка$O$ лежить між$A$$A'$$B$ і між ними і$B'$ одночасно.

Пропозиція$\PageIndex{1}$

Вертикальні кути мають рівні міри.

Доказ

Припустимо, що кути$AOB$ і$A'OB'$ вертикальні. Зверніть увагу, що$\angle AOA'$ і$\angle BOB'$ є прямими. Тому,$\measuredangle AOA' = \measuredangle BOB' = \pi$.

$2021-02-02 пнг$

Звідси випливає, що

\[\begin{array} {rcl} {0} & = & {\measuredangle AOA' - \measuredangle BOB' \equiv} \\ {} & equiv & {\measuredangle AOB + \measuredangle BOA' - \measuredangle BOA' - \measuredangle A'OB' \equiv} \\ {} & \equiv & {\measuredangle AOB - \measuredangle A'OB'.} \end{array}\]

Так як$-\pi < \measuredangle AOB \le \pi$ і$-\pi < \measuredangle A'OB' \le \pi$, ми отримуємо, що$\measuredangle AOB = \measuredangle A'OB'$.

Вправа$\PageIndex{1}$

Припустимо,$O$ це середина для обох сегментів$[AB]$ і$[CD]$. Доведіть, що$AC = BD$.

Підказка: Застосовуючи пропозицію 2.5.1, ми отримуємо це$\measuredangle AOC = \measuredangle BOD$. Залишилося застосувати Аксіому IV.