2.4: Прямий кут

Last updated
Save as PDF

Page ID: 59136

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Якщо$\measuredangle AOB = \pi$, ми говоримо, що$\angle AOB$ це прямий кут. Зверніть увагу, що за пропозицією 2.3.2, якщо$\angle AOB$ є прямим, то так є$\angle BOA$.

Ми говоримо, що точка$O$ лежить між точками$A$ і$B$, якщо$O \ne A$$O \ne B$, і$O \in [AB]$.

Теорема$\PageIndex{1}$

$AOB$Кут прямий, якщо і тільки якщо$O$ лежить між$A$ і$B$.

Доказ

За пропозицією 2.2.2 ми можемо припустити, що$OA = OB = 1$.

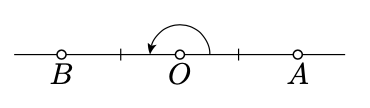
$2021-02-02 пнг$

Частина «Якщо». Припустимо$O$ брехня між$A$ і$B$. Набір$\alpha = \measuredangle AOB$.

Застосовуючи Axiom IIIa, отримуємо полустрочку$[OA')$ таку, що$\alpha = \measuredangle BOA'$. За пропозицією 2.2.2 можна припустити, що$OA' = 1$. Відповідно до Аксіоми IV,

$\triangle AOB \cong \triangle BOA'$.

Припустимо, що$f$ позначає відповідний рух площини;$f$ тобто рух таке$f(A) = B$, що$f(O) = O$, і$f(B) = A'$.

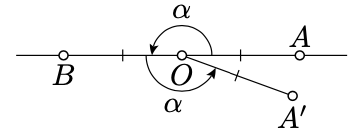
$2021-02-02 пнг$

Тоді

$O = f(O) \in f(AB) = (A'B)$.

Тому обидва рядки$(AB)$ і$(A'B)$ містять$B$ і$O$. За аксіомою II,$(AB) = (A'B)$.

За визначенням прямої,$(AB)$ містить рівно дві точки$A$ і$B$ на відстані 1 від$O$. Так як$OA' = 1$ і$A' \ne B$, ми отримуємо, що$A = A'$.

За аксіомою IIiB та пропозицією 2.3.1 ми отримуємо, що

\[\begin{array} {rcl} {2 \cdot \alpha} & = & {\measuredangle AOB + \measuredangle BOA' =} \\ {} & = & {\measuredangle AOB + \measuredangle BOA \equiv} \\ {} & equiv & {\measuredangle AOA =} \\ {} & = & {0} \end{array}\]

Тому, за вправою 1.8.1$\alpha$, або 0, або$\pi$.

Оскільки$[OA) \ne [OB)$ ми маємо це$\alpha \ne 0$, див. Вправа 2.3.1. Тому,$\alpha = \pi$.

«Тільки якщо» частина. Припустимо, що$\measuredangle AOB = \pi$. Розглянемо лінію$(OA)$ і вибираємо точку$B'$ на$(OA)$ так, щоб$O$ лежала між$A$ і$B'$.

Зверху ми маємо це$\measuredangle AOB' = \pi$. Застосовуючи Axiom IIia, отримуємо це$[OB) = [OB')$. Зокрема,$O$ лежить між$A$ і$B$.

Трикутник$ABC$ називається виродженим якщо$A, B$, і$C$ лежати на одній лінії. Наступний наслідок є лише переформулюванням теореми 2.4.1.

Слідство$\PageIndex{1}$

Трикутник вироджується тоді і тільки тоді, коли один з його кутів дорівнює$\pi$ або 0. Більше того, у виродженому трикутнику кутові заходи 0, 0, і$\pi$.

Вправа$\PageIndex{1}$

Показати, що три різні точки$A, O$, і$B$ лежать на одній лінії, якщо і тільки якщо

$2 \cdot \measuredangle AOB \equiv 0$.

Підказка: Застосувати пропозицію 2.3.1, теорему 2.4.1 та вправу 1.8.1.

Вправа$\PageIndex{2}$

$C$Дозволяти$A, B$ і бути три точки відмінні від$O$. Покажіть, що$B, O$ і$C$ лежати на одному рядку, якщо і тільки якщо

$2 \cdot \measuredangle AOB \equiv 2 \cdot \measuredangle AOC$.

Підказка: Аксіома IIIб,$2 \cdot \measuredangle BOC \equiv 2 \cdot \measuredangle AOC - 2 \cdot \measuredangle AOB = 0$. За вправою 1.8.1 він має на увазі, що$\measuredangle BOC$ це або 0 або$\pi$. Залишається застосувати Exercsie 2.3.1 і Theorem 2.4.1 відповідно в цих двох випадках.

Вправа$\PageIndex{3}$

Показати, що існує невироджений трикутник.

Відповідь

Закріпіть дві точки$A$ і$B$ передбачені аксіомою I.

Виправте дійсне число$0 < \alpha < \pi$. За аксіомою IIia є$C$ такий момент, що$\measuredangle ABC = \alpha$. Використовуйте Proposition 2.2.1, щоб показати, що$\triangle ABC$ є невиродженим.