1.10: Конгруентні трикутники

Last updated
Save as PDF

Page ID: 59186

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Наша наступна мета - надати суворе значення для (iv) Розділу 1.1. Для цього ми вводимо поняття конгруентних трикутників, тому замість «якщо ми обертаємо або зсуваємо, ми не побачимо різниці», ми говоримо, що для трикутників конгруентність бічного кута тримає; тобто два трикутники є конгруентними, якщо вони мають дві пари рівних сторін і однаковий кут вимірювання між цими сторонами .

Впорядкована трійка різних точок в метричному просторі$\mathcal{X}$, скажімо$A, B, C$, називається трикутником$ABC$ (коротко$\triangle ABC$). Зверніть увагу, що$ACB$ трикутники$ABC$ і вважаються різними.

Два трикутника$A'B'C'$ і$ABC$ називаються конгруентними (його можна записати як$\triangle A'B'C' \cong \triangle ABC$), якщо є рух$f: \mathcal{X} \to \mathcal{X}$ такий, що

$A' = f(A)$,$B' = f(B)$ і$C' = f(C)$.

$\mathcal{X}$Дозволяти бути метричний простір, і$f, g: \mathcal{X} \to \mathcal{X}$ бути два рухи. Відзначимо, що зворотне$f^{-1}: \mathcal{X} \to \mathcal{X}$, а також композиція$f \circ g: \mathcal{X} \to \mathcal{X}$ - це теж рухи.

Звідси випливає, що$\cong$ "" - це відношення еквівалентності; тобто будь-який трикутник, конгруентний собі, і наступні дві умови дотримуються:

Якщо$\triangle A'B'C' \cong \triangle ABC$, то$\triangle ABC \cong \triangle A'B'C'$.
Якщо$\triangle A''B''C'' \cong \triangle A'B'C'$ і$\triangle A'B'C' \cong \triangle ABC$, то
\[\triangle A''B''C'' \cong \triangle ABC.\]

Зверніть увагу, що якщо$\triangle A'B'C' \cong \triangle ABC$, то$AB = A'B', BC = B'C'$ і$CA = C'A'$.

Для дискретної метрики, а також деяких інших показників, конверс також тримається. Наступний приклад показує, що він не тримається в літаку Манхеттена:

Приклад$\PageIndex{1}$

Розглянемо три$A = (0, 1), B = (1, 0)$ пункти і$C = (-1, 0)$ на Манхеттенському літаку$(\mathbb{R}^2, d_1)$. Зверніть увагу, що

\[d_1 (A, B) = d_1 (A, C) = d_1 (B, C) = 2.\]

З одного боку,

$\triangle ABC \cong \triangle ACB.$

Дійсно, карта$(x, y) \mapsto (-x, y)$ - це рух,$(\mathbb{R}^2, d_1)$ який посилає$A \mapsto A, B \mapsto C$, і$C \mapsto B$.

З іншого боку,

$\triangle ABC \not\cong \triangle BCA.$

$2021-01-28 4.03.57.png$

Дійсно, аргументуючи протиріччям, припускайте, що$\triangle ABC \cong \triangle BCA$; тобто є рух$f$$(\mathbb{R}^2, d_1)$ того, що послати$A \mapsto B, B \mapsto C,$ і$C \mapsto A$.

Ми говоримо, що$M$ це середина$A$ і$B$ якщо

$d_1(A, M) = d_1(B, M) = \dfrac{1}{2} \cdot d_1(A, B).$

Зверніть увагу, що точка$M$ є середньою точкою$A$ і$B$ якщо і тільки тоді, коли$f(M)$ є серединою$B$ і$C$.

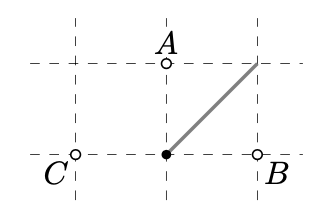
Набір середніх точок для$A$ і$B$ нескінченний, він містить всі точки$(t, t)$ для$t \in [0, 1]$ (це сірий відрізок на малюнку вище). З іншого боку, середина для$B$ і$C$ є унікальною (це чорна точка на малюнку). Таким чином, карта$f$ не може бути об'єктивною — протиріччям.