1.7: Кути

Last updated
Save as PDF

Page ID: 59194

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Наша наступна мета - ввести кути та кутові заходи; після цього твердження «ми можемо виміряти кути» стане суворим; див. (iii) Розділ 1.1.

Впорядкована пара напівліній, які починаються в одній точці, називається кутом. Кут$AOB$ (також позначається$\angle AOB$) - пара напівліній$[OA)$ і$[OB)$. У цьому випадку точка$O$ називається вершиною кута.

Інтуїтивно вимір кута говорить про те, наскільки потрібно повернути першу півлінію проти годинникової стрілки, таким чином вона отримує положення другої половини кута. Приймається повний поворот$2 \cdot \pi$; він відповідає вимірюванню кута в радіанах. (На деякий час ви можете подумати, що$\pi$ це позитивне реальне число, яке вимірює розмір половини обороту в певних одиницях. Його конкретне значення не$\pi \approx 3.14$ буде мати значення протягом тривалого часу.

Кутова міра$\angle AOB$ позначається$\measuredangle AOB$; це дійсне число в інтервалі$(-\pi, \pi]$.

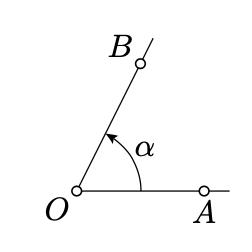
$2021-01-28 2.56.01.PNG$

Позначення$\angle AOB$ і$\measuredangle AOB$ виглядають схожі; вони також мають близькі, але різні значення, які краще не плутати. Наприклад, рівність$\angle AOB = \angle A'O'B'$ означає, що$[OA) = [O'A')$ і$[OB) = [O'B')$; зокрема,$O = O'$. З іншого боку, рівність$\measuredangle AOB = \measuredangle A'O'B'$ означає лише рівність двох дійсних чисел; у цьому випадку$O$ може відрізнятися від$O'$.

Ось перша властивість вимірювання кута, яка стане частиною аксіоми.

Дано$[OA)$ полустрочку і$\alpha \in (-\pi, \pi]$ є унікальна напівлінія$[OB)$ така, що$\measuredangle AOB = \alpha$.