11.8: Відображення та симетрія
- Page ID
- 62859
Відображення і симетрія в лінії
Припустимо, у нас є лінія,\(S\) а точка\(z_1\) не на\(S\). Відбиття\(z_1\) in\(S\) - це точка\(z_2\) так,\(S\) що перпендикулярна бісектриса до відрізка лінії\(\overline{z_1 z_2}\). Оскільки існує рівно одна така точка\(z_2\), відображення точки в прямій є унікальним.
Якщо\(z_2\) це відображення\(z_1\) в\(S\), ми говоримо, що\(z_1\) і\(z_2\) симетричні по відношенню до лінії\(S\).
На малюнку нижче точки\(z_1\) і\(z_2\) симетричні в\(x\) -осі. Точки\(z_3\) і\(z_4\) симетричні в лінії\(S\).
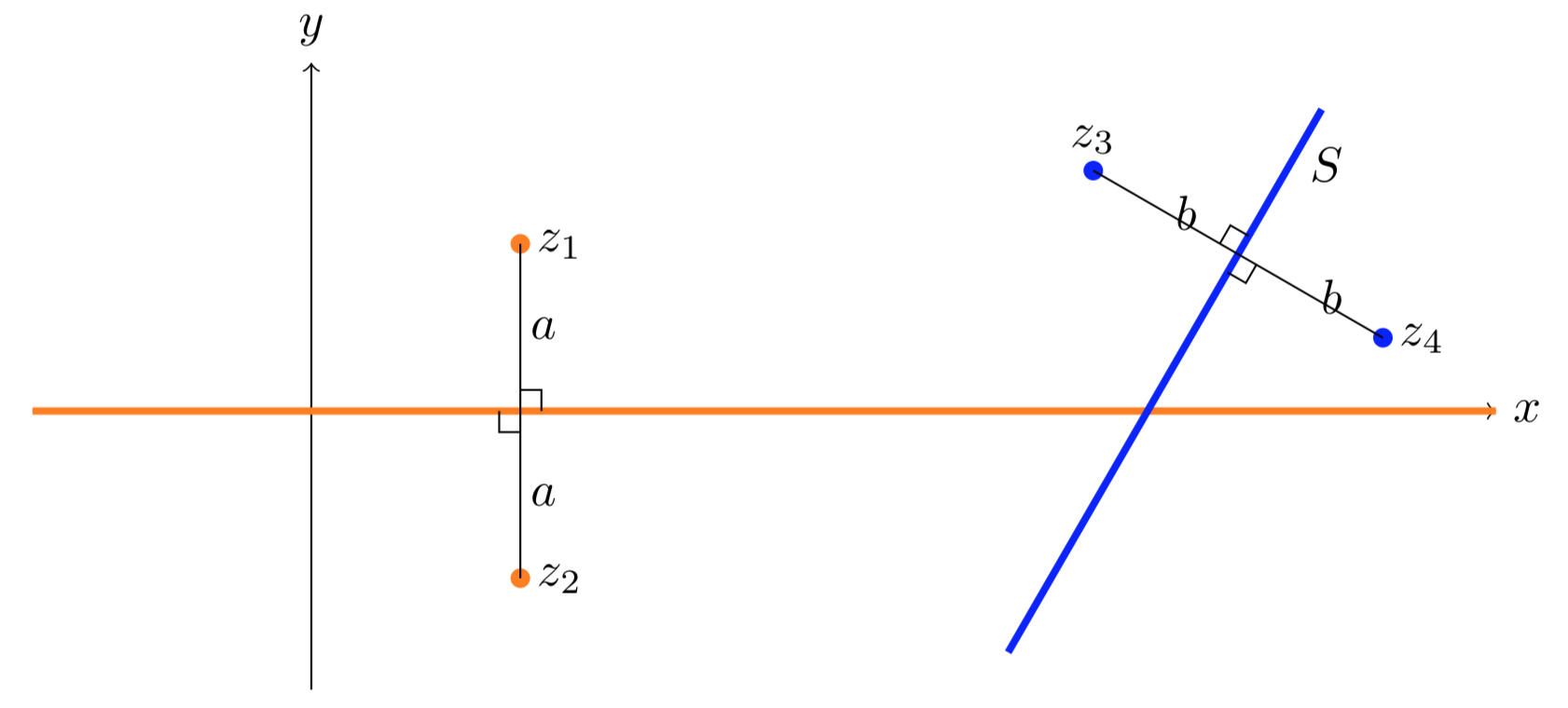
Для того, щоб визначити відображення точки в колі, нам потрібно попрацювати трохи більше. Озираючись назад на попередній приклад, ми можемо показати наступне.
Якщо\(z_1\) і\(z_2\) симетричні в лінії\(S\), то будь-яке коло наскрізь\(z_1\) і\(z_2\) перетинається\(S\) ортогонально.
- Доказ
-
Викликати коло\(C\). \(S\)Оскільки перпендикулярна бісектриса хорди\(C\), центр\(C\) лежить на\(S\). Тому\(S\) є радіальною лінією, тобто вона перетинається\(C\) ортогонально.
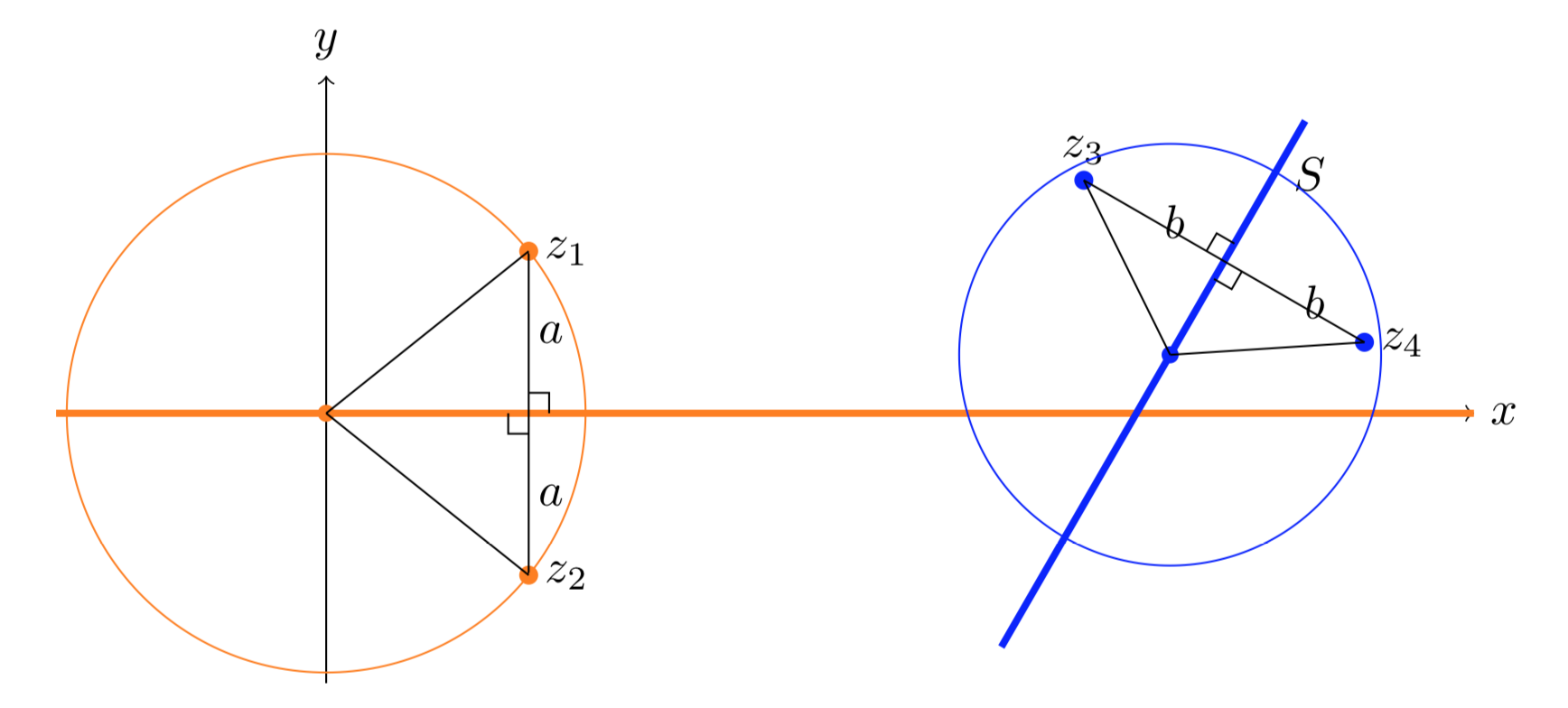
Кола через симетричні точки перетинають лінію під прямим кутом.
Відображення і симетрія в колі
Ми адаптуємо це для нашого визначення відображення в колі. Щоб логіка текла правильно, потрібно почати з визначення симетричних пар точок.
Припустимо,\(S\) це лінія або коло. Пара точок\(z_1, z_2\) називається симетричною відносно того,\(S\) якщо кожна лінія або коло через дві точки перетинаються\(S\) ортогонально.
Спочатку ми констатуємо майже тривіальний факт.
Дробові лінійні перетворення зберігають симетрію. Тобто якщо\(z_1, z_2\) симетричні по лінії або колу\(S\), то, для FLT\(T\),\(T(z_1)\) і\(T(z_2)\) симетричні в\(T(S)\).
- Доказ
-
Визначення симетрії відбувається з точки зору ліній і кіл, і кутів. Дробові лінійні перетворення відображають лінії та кола на лінії та кола і, будучи конформними, зберігають кути.
Припустимо,\(S\) це лінія або коло\(z_1\), а точка не на\(S\). Є унікальний момент\(z_2\) такий, що пара\(z_1, z_2\) симетрична в\(S\).
- Доказ
-
\(T\)Дозволяти дробове лінійне перетворення, яке\(S\) відображає на лінію. Ми знаємо, що\(w_1 = T(z_1)\) має унікальне відображення\(w_2\) в цьому рядку. Так як\(T^{-1}\) зберігає симетрію,\(z_1\) і\(z_2 = T^{-1} (w_2)\) симетричні в\(S\). Так як\(w_2\) унікальна точка симетрична до того\(w_1\) ж, вірно для\(z_2\) vis-a-vis\(z_1\). Це все показано на малюнку нижче.
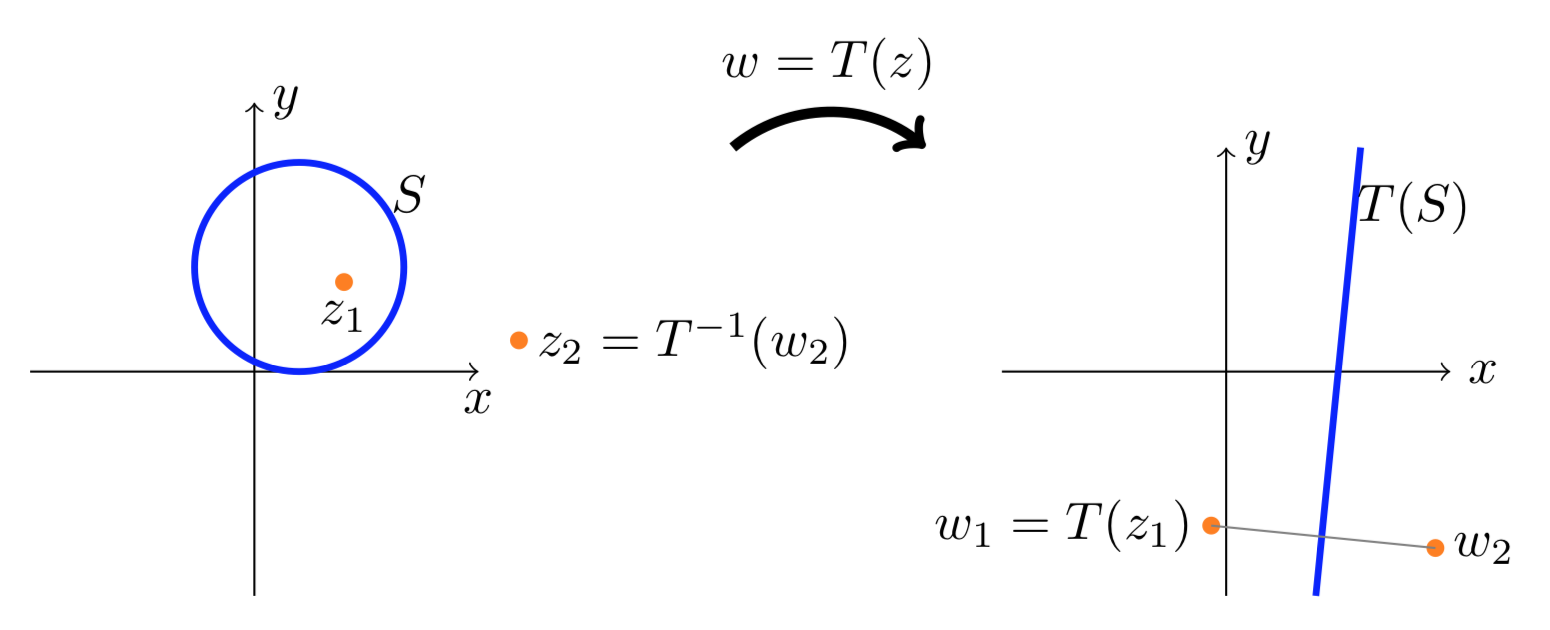
Тепер ми можемо визначити відображення в колі.
Точка\(z_2\) в теоремі 11.8.1 називається відображенням\(z_1\) в\(S\).
Відображення в одиничному колі
Використовуючи функцію збереження симетрії дробових лінійних перетворень, ми починаємо з лінії і трансформуємо в коло. \(R\)Дозволяти реальна вісь і\(C\) одиниця окружності. Ми знаємо FLT
\[T(z) = \dfrac{z - i}{z + i}\]
карти\(R\) до\(C\). Ми також знаємо, що точки\(z\) і\(\overline{z}\) симетричні в\(R\). Тому
\[w_1 = T(z) = \dfrac{z - i}{z + i} \ \ \ \text{and} \ \ \ w_2 = T(\overline{z}) = \dfrac{\overline{z} - i}{\overline{z} + i}\]
симетричні в\(D\). Дивлячись на формули, зрозуміло, що\(w_2 = 1/\overline{w_1}\). Це досить важливо, щоб ми виділили його як теорему.
Відображення\(z = x + iy = re^{i \theta}\) в одиничному колі
\[\dfrac{1}{\overline{z}} = \dfrac{z}{|z|^2} = \dfrac{x + iy}{x^2 + y^2} = \dfrac{e^{i \theta}}{r}.\]
Розрахунки з\(1/\overline{z}\) все тривіальні.
- Можна, але більш виснажливим і менш проникливим, дійти до цієї теореми прямим розрахунком.
- Якщо\(z\) знаходиться на одиничному колі, то\(1/\overline{z} = z\). Тобто\(z\) є власне відображення в одиничному колі —як і повинно бути.
- Центр кола 0 симетричний точці в\(\infty\).
На малюнку нижче показані три пари точок, симетричних в одиничному колі:
\(z_1 = 2; \ w_1 = \dfrac{1}{2}, \ z_2 = 1 + i; \ w_2 = \dfrac{1 + i}{2},\ z_3 = -2 + i; \ w_3 = \dfrac{-2 + i}{5}.\)
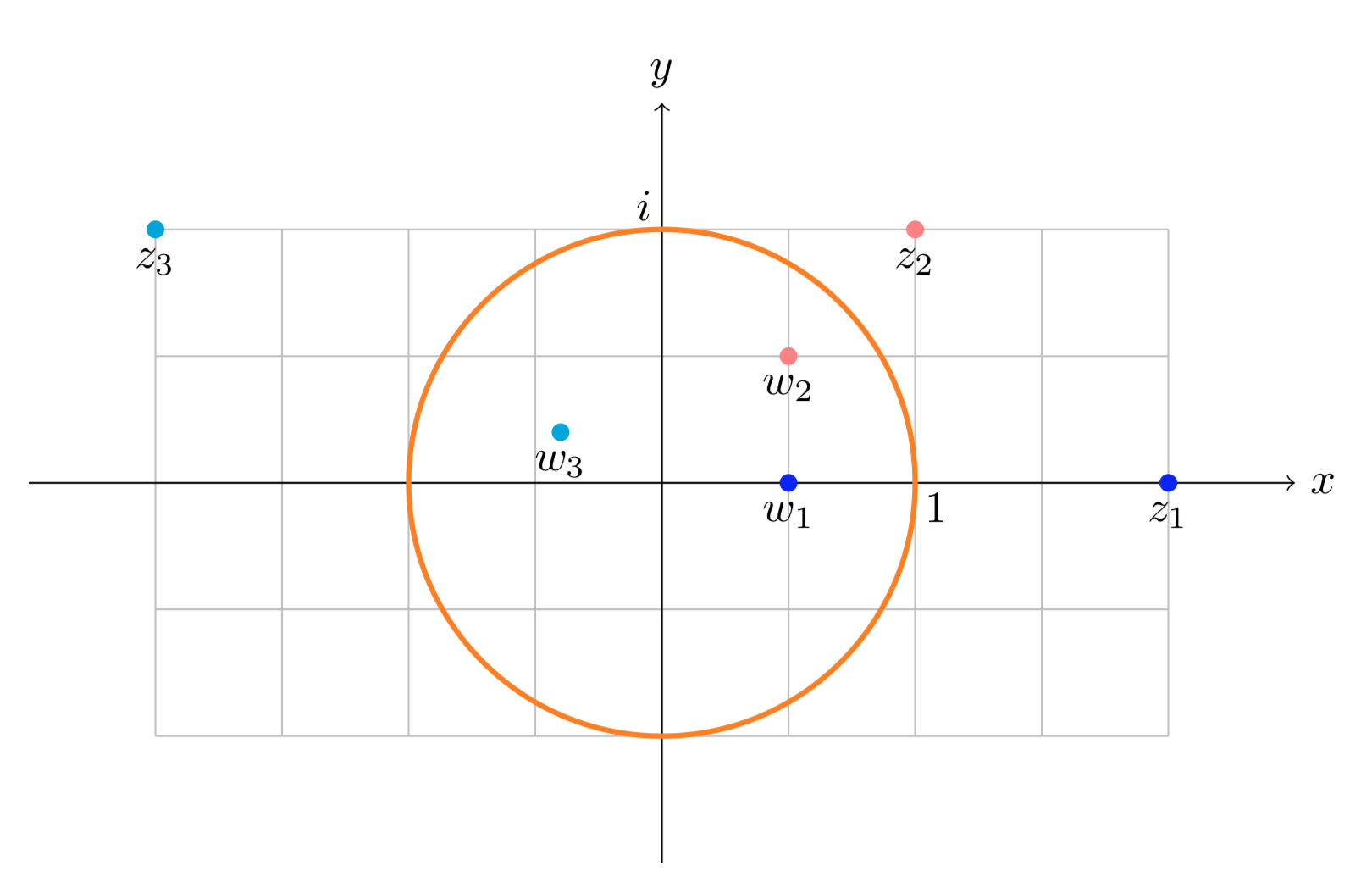
Пари точок\(z_j\):\(w_j\) симетричні в одиничному колі.
Припустимо\(S\),\(z_1\) це коло\(|z| = R\) і пінта не на\(S\). Знайдіть відображення\(z_1\) в С.
Рішення
Наша стратегія полягає в тому,\(S\) щоб зіставити одиничне коло, знайти відображення, а потім зіставити одиничне коло назад\(S\).
Почніть з карти\(T(z) = w = z/R\). Чітко\(T\)\(S\) відображає одиничний коло і
\[w_1 = T(z_1) = z_1/R.\]
Відображення\(w_1\) є
\[w_2 = 1/\overline{w_1} = R/\overline{z}_1.\]
Відображення назад від одиничного кола у\(T^{-1}\) нас є
\[z_2 = T^{-1} (w_2) = Rw_2 = R^2/\overline{z}_1.\]
Тому відображення\(z_1\) є\(R^2/\overline{z}_1.\)
Ось три пари точок, симетричних по колу радіуса 2. Зверніть увагу, що це та ж цифра, що і вище, з усім подвоєним.
\(z_1 = 4;\ w_1 = 1,\ z_2 = 2 + 2i;\ w_2 = 1 + i, \ z_3 = -4 + 2i;\ w_3 = \dfrac{-4 + 2i}{5}.\)
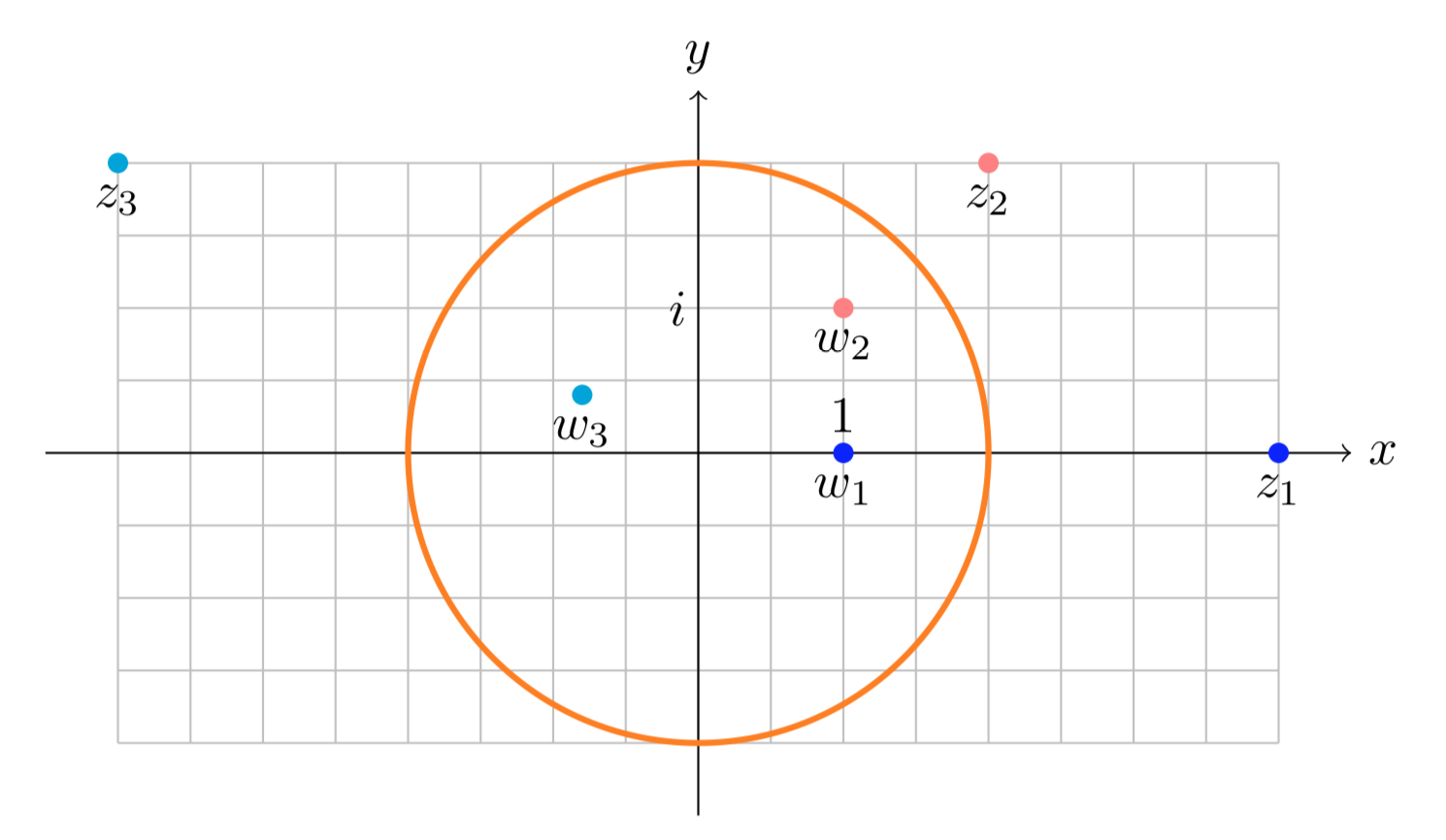
Пари точок\(z_j\);\(w_j\) симетричні по колу радіуса 2.
Знайти відображення\(z_1\) в колі радіуса з\(R\) центром в\(c\).
Рішення
Нехай\(T(z) = (z - c)/R\). \(T\)відображає коло з центром\(c\) до одиничного кола. Зворотна карта
\[T^{-1} (w) = Rw + c.\]
Отже, відображення\(z_1\) задається відображенням\(z\) до\(T(z)\), відображаючи це в одиничному колі, і відображення назад до вихідної геометрії с\(T^{-1}\). Тобто відображення\(z_2\) є
\[z_1 \to \dfrac{z_1 - c}{R} \to \dfrac{R}{\overline{z_1 - c}} \to z_2 = \dfrac{R^2}{\overline{z_1 - c}} + c.\]
Тепер ми можемо зафіксувати наступний важливий факт.
Для кола\(S\) з центром\(c\) пара\(c\),\(\infty\) симетрична по відношенню до кола.
- Доказ
-
Це безпосередній наслідок формули відображення точки по колу. Наприклад, відображення в\(z\) одиничному колі є\(1/\overline{z}\). Отже, відображення 0 - нескінченність.
Показати, що якщо коло і лінія не перетинаються, то є пара точок\(z_1, z_2\), які симетричні по відношенню як до лінії, так і по колу.
Рішення
Зсуваючи, масштабуючи та обертаючи, ми можемо знайти дробове лінійне перетворення\(T\), яке відображає коло та лінію до наступної конфігурації: Коло відображається на одиничному колі, а лінія - до вертикальної лінії\(x = a > 1\).
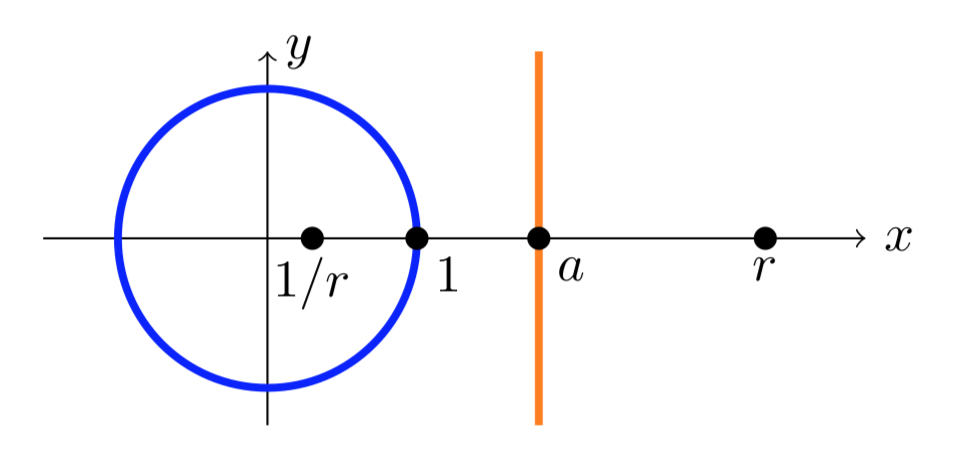
Для будь-яких реальних\(r\),\(w_1 = r\) і\(w_2 = 1/r\) симетричні в одиничному колі. Ми можемо вибрати конкретні\(r\) так, щоб\(r\) і\(1/r\) були рівновіддалені від\(a\), тобто також симетричні в лінії\(x = a\). Геометрично зрозуміло, що це можна зробити. Алгебраїчно вирішуємо рівняння
\[\dfrac{r + 1/r}{2} = a \ \ \Rightarrow \ \ r^2 - 2ar + 1 = 0 \ \ \Rightarrow \ \ r = a + \sqrt{a^2 - 1} \ \ \Rightarrow \ \ \dfrac{1}{r} = a - \sqrt{a^2 - 1}.\]
Таким чином\(z_1 = T^{-1} (a + \sqrt{a^2 - 1})\) і\(z_2 = T^{-1} (a - \sqrt{a^2 - 1})\) є необхідними балами.
Показати, що якщо два кола не перетинаються, то є пара точок\(z_1, z_2\), симетричних по відношенню до обох кіл.
Рішення
Використовуючи дробове лінійне перетворення, яке відображає одне з кіл на пряму (а іншу - на коло), ми можемо зменшити проблему до того, що в попередньому прикладі.
Показати, що будь-які два кола, які не перетинаються, можуть бути відображені відповідно до концентричних кіл.
Рішення
Викликати кола\(S_1\) і\(S_2\). У попередньому прикладі почніть з пари точок\(z_1, z_2\), які симетричні в обох колах. Далі виберіть дробове лінійне перетворення\(T\), яке відображає\(z_1\) 0 та\(z_2\) нескінченність. Наприклад,
\[T(z) = \dfrac{z - z_1}{z - z_2}.\]
Так як\(T\) зберігає симетрію 0 і\(\infty\) симетричні в колі\(T(S_1)\). Це означає, що 0 є центром\(T(S_1)\). Аналогічно 0 є центром\(T(S_2)\). Таким чином,\(T(S_1)\) і\(T(S_2)\) є концентричними.