11.9: Тече навколо циліндрів
- Page ID
- 62842
Теорема про коло Мілна-Томсона
Теорема Мілна-Томсона дозволяє вставити коло в двовимірний потік і подивитися, як регулюється потік. Спочатку викладемо і доведемо теорему.
Якщо\(f(z)\) складний потенціал з усіма його особливостями зовні,\(|z| = R\) то
\[\Phi (z) = f(z) + \overline{f(\dfrac{R^2}{\overline{z}})}\]
це складний потенціал з раціоналізацією\(|z| = R\) та тими ж особливостями, що і\(f\) в регіоні\(|z| > R\).
- Доказ
-
Спочатку зверніть увагу, що\(R^2/\overline{z}\) це відображення\(z\) в колі\(|z| = R\).
Далі ми повинні побачити, що\(\overline{f(R^2/\overline{z})}\) є аналітичним для\(|z| > R\). За припущенням\(f(z)\) є аналітичним для\(|z| < R\), тому його можна виразити як ряд Тейлора
\[f(z) = a_0 + a_1 z + a_2 z^2 + \ ...\]
Тому,
\[\overline{f(\dfrac{R^2}{\overline{z}})} = \overline{a_0} + \overline{a_1} \dfrac{R^2}{z} + \overline{a_2} (\dfrac{R^2}{z})^2 + \ ...\]
Всі особливості\(f\) знаходяться поза межами\(|z| = R\), тому серія Тейлора в Рівнянні 11.10.2 сходиться для\(|z| \le R\). Це означає, що ряд Лорана в рівнянні 11.10.3 сходиться для\(|z| \ge R\). Тобто\(\overline{f(R^2/\overline{z})}\) є аналітичним\(|z| \ge R\), тобто не вводить жодних сингулярів\(\Phi (z)\) назовні\(|z| = R\).
Останнє, що потрібно показати,\(|z| = R\) це обтічність для\(\Phi (z)\). Це випливає, тому що для\(z = Re^{i \theta}\)
\[\Phi (Re^{i \theta}) = f(Re^{i \theta} + \overline{f(Re^{i \theta})}\]
це реально. Тому
\[\psi (Re^{i \theta} = \text{Im} (\Phi (Re^{i \theta}) = 0.\]
Приклади
Думайте про те\(f(z)\), що представляє потік, можливо, з джерелами або вихорами зовні\(|z| = R\). Потім\(\Phi (z)\) представляє новий потік, коли в потоці розміщується кругова перешкода. Ось кілька прикладів.
Ми знаємо з теми 6, що\(f(z) = z\) є складним потенціалом для рівномірного потоку праворуч. Отже,
\[\Phi (z) = z + R^2/z\]
є потенціалом для рівномірного потоку навколо кола радіуса,\(R\) зосередженого на початку координат.
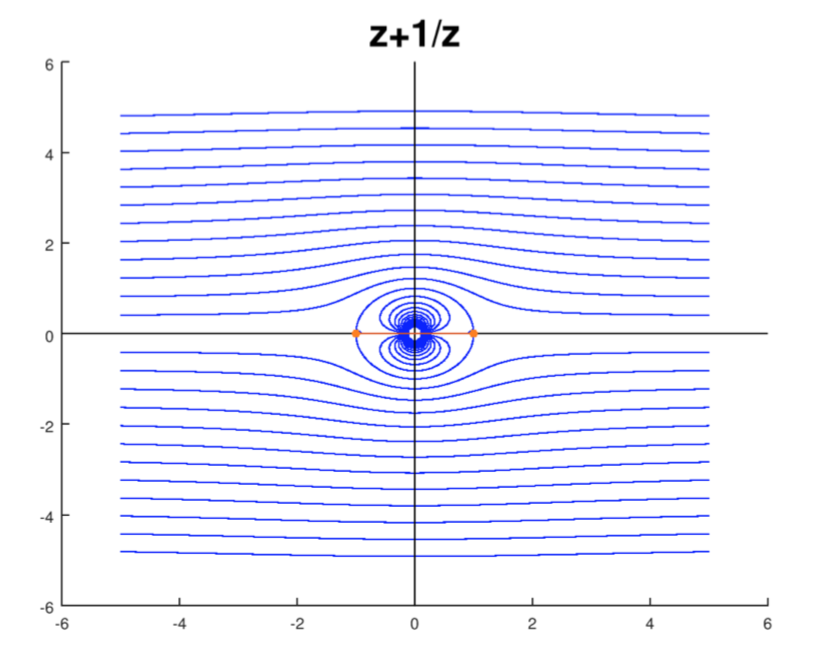
Рівномірний потік по колу
Просто тому, що вони виглядають красиво, фігура включає в себе обтічні лінії всередині кола. Вони не взаємодіють з потоком поза колом.
Зверніть увагу, що при\(z\) отриманні великого потоку виглядає рівномірним. Ми можемо бачити це аналітично, тому що
\[\Phi '(z) = 1 - R^2/z^2\]
переходить до 1, як\(z\) стає великим. (Нагадаємо, що поле швидкості є (\(\phi _x, \phi _y\)), де\(\Phi = \phi + i \psi \ ...\))
Тут джерело знаходиться в\(z = -2\) (поза одиничним колом) зі складним потенціалом
\[f(z) = \log (z + 2).\]
З відповідною гілкою вирізати особливості\(f\) знаходяться також зовні\(|z| = 1\). Таким чином, ми можемо застосувати Мілна-Томсона і отримати
\[\Phi (z) = \log (z + 2) + \overline{\log (\dfrac{1}{\overline{z}} + 2)}\]
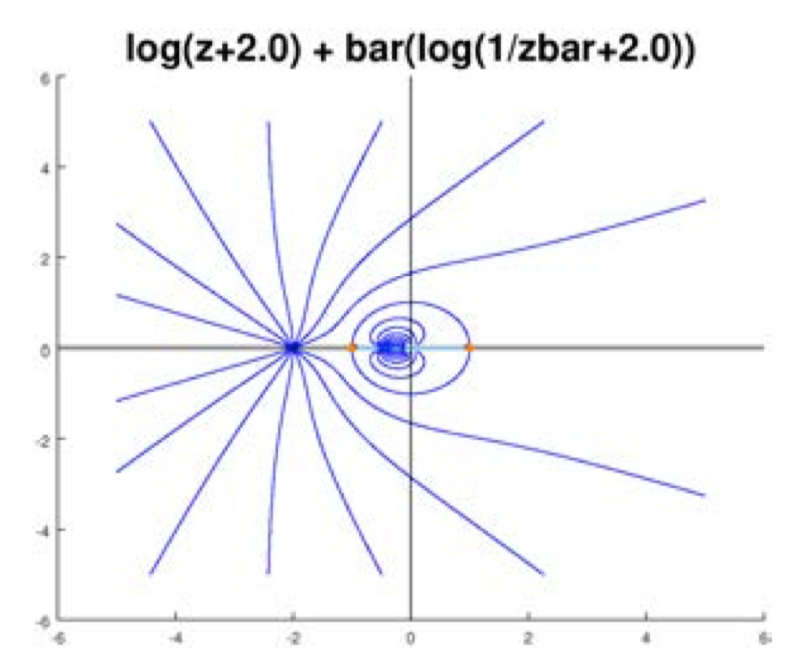
Джерело течії по колу
Ми знаємо, що далеко від походження потік повинен виглядати так само, як потік з лише джерелом на\(z = -2\).
Давайте розберемося в цьому аналітично. Спочатку констатуємо корисний факт:
Якщо\(g(z)\) аналітичний, то так є\(h(z) = \overline{g(\overline{z})}\) і\(h'(z) = \overline{g'(\overline{z})}\).
- Доказ
-
Використовуйте серію Тейлора для\(g\) отримання серії Тейлора для,\(h\) а потім порівняйте\(h'(z)\) і\(\overline{g'(\overline{z})}\).
Використовуючи це, ми маємо
\[\Phi ' (z) = \dfrac{1}{z + 2} - \dfrac{1}{z(1 + 2z)}\]
Для великих\(z\) другий термін розпадається набагато швидше, ніж перший, тому
\[\Phi ' (z) \approx \dfrac{1}{z + 2}.\]
Тобто далеко не поле швидкості виглядає так само\(z = 0\), як поле швидкості для\(f(z)\), тобто поле швидкості джерела при\(z = -2\).
Якщо ми використовуємо
\[g(z) = z^2\]
ми можемо перетворити потік з верхньої півплощини в перший квадрант
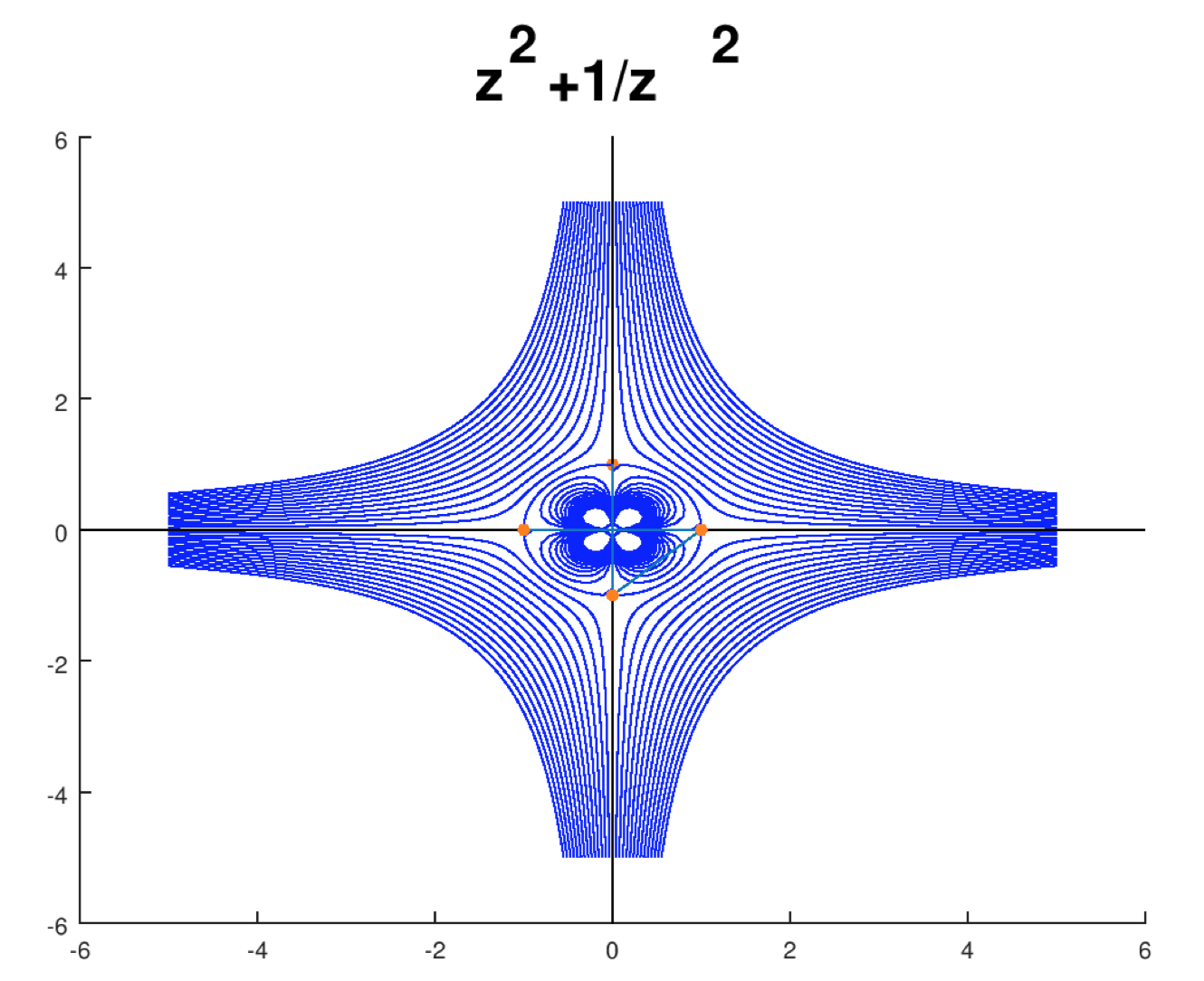
Джерело протікає навколо чверті кругового кута
