Skip to main content
LibreTexts - Ukrayinska

11.5E: Вправи

  1. Last updated
  2. Save as PDF
  • Page ID
    59820

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Практика робить досконалим

    Вправа\(\PageIndex{13}\) Graph a Hyperbola with Center at \((0,0)\)

    У наступних вправах граф.

    1. \(\frac{x^{2}}{9}-\frac{y^{2}}{4}=1\)
    2. \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\)
    3. \(\frac{x^{2}}{16}-\frac{y^{2}}{25}=1\)
    4. \(\frac{x^{2}}{9}-\frac{y^{2}}{36}=1\)
    5. \(\frac{y^{2}}{25}-\frac{x^{2}}{4}=1\)
    6. \(\frac{y^{2}}{36}-\frac{x^{2}}{16}=1\)
    7. \(16 y^{2}-9 x^{2}=144\)
    8. \(25 y^{2}-9 x^{2}=225\)
    9. \(4 y^{2}-9 x^{2}=36\)
    10. \(16 y^{2}-25 x^{2}=400\)
    11. \(4 x^{2}-16 y^{2}=64\)
    12. \(9 x^{2}-4 y^{2}=36\)
    Відповідь

    1.

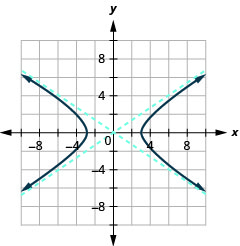
    Графік показує вісь x та y, які обидва працюють у негативному та додатному напрямках, але з немаркованими інтервалами, при цьому асимптоти y дорівнює плюс-мінус дві третини разів x, а гілки, які проходять через вершини (плюс або мінус 3, 0) і відкриті вліво і вправо.
    Малюнок 11.4.33

    3.

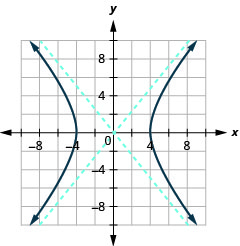
    На графіку показані осі x та осі y, які обидва проходять у негативному та додатному напрямках з асимптотами y дорівнює плюс-мінус п'ять четвертих разів x, а гілки, які проходять через вершини (плюс або мінус 4, 0) і відкриті вліво і вправо.
    Малюнок 11.4.34

    5.

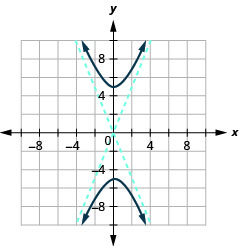
    На графіку показані вісь x та осі y, які обидва проходять у негативному та додатному напрямках з асимптотами y дорівнює плюс-мінус п'ятиполовинкам раз x, а гілки, які проходять через вершини (0, плюс або мінус 5) і відкриваються вгору і вниз.
    Малюнок 11.4.35

    7.

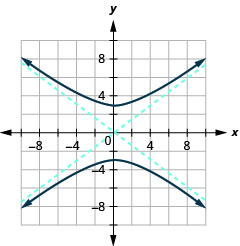
    На графіку показані вісь x та осі y, які обидва проходять у негативному та додатному напрямках з асимптотами y дорівнює плюс-мінус три чверті разів x, а гілки, які проходять через вершини (0, плюс або мінус 3) і відкриваються вгору і вниз.
    Малюнок 11.4.36

    9.

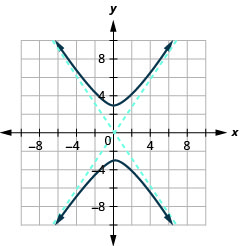
    На графіку показані вісь x та осі y, які обидва проходять у негативному та додатному напрямках з асимптотами y дорівнює плюс-мінус триполовинки разів x, а гілки, які проходять через вершини (0, плюс або мінус 3) і відкриваються вгору і вниз.
    Малюнок 11.4.37

    11.

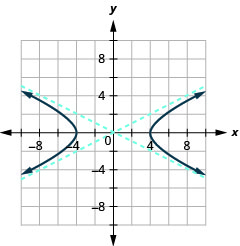
    На графіку показані вісь x та осі y, які обидва проходять у негативному та додатному напрямках з асимптотами y дорівнює плюс-мінус в півтора рази x, а гілки, які проходять через вершини (плюс або мінус 4, 0) і відкриваються вліво і вправо.
    Малюнок 11.4.38
    Вправа\(\PageIndex{14}\) Graph a Hyperbola with Center at \((h,k)\)

    У наступних вправах граф.

    1. \(\frac{(x-1)^{2}}{16}-\frac{(y-3)^{2}}{4}=1\)
    2. \(\frac{(x-2)^{2}}{4}-\frac{(y-3)^{2}}{16}=1\)
    3. \(\frac{(y-4)^{2}}{9}-\frac{(x-2)^{2}}{25}=1\)
    4. \(\frac{(y-1)^{2}}{25}-\frac{(x-4)^{2}}{16}=1\)
    5. \(\frac{(y+4)^{2}}{25}-\frac{(x+1)^{2}}{36}=1\)
    6. \(\frac{(y+1)^{2}}{16}-\frac{(x+1)^{2}}{4}=1\)
    7. \(\frac{(y-4)^{2}}{16}-\frac{(x+1)^{2}}{25}=1\)
    8. \(\frac{(y+3)^{2}}{16}-\frac{(x-3)^{2}}{36}=1\)
    9. \(\frac{(x-3)^{2}}{25}-\frac{(y+2)^{2}}{9}=1\)
    10. \(\frac{(x+2)^{2}}{4}-\frac{(y-1)^{2}}{9}=1\)
    Відповідь

    1.

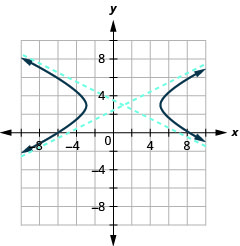
    Графік показує вісь x та вісь y, які обидва проходять у негативному та позитивному напрямках з центром (1, 3) асимптотою, яка проходить через (негативні 3, 1) та (5, 5) та асимптоту, яка проходить через (5, 1) та (негативні 3, 5), та гілки, що проходять через вершини (негативні 3, 3) та (5, 3) та відкривається вліво і вправо.
    Малюнок 11.4.39

    3.

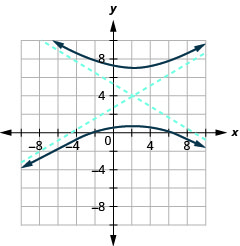
    Графік показує вісь x та вісь y, які обидва проходять у негативному та позитивному напрямках з центром (1, 3) асимптотою, яка проходить через (негативні 3, 1) та (5, 5) та асимптоту, яка проходить через (5, 1) та (негативні 3, 5), та гілки, що проходять через вершини (негативні 3, 3) та (5, 3) та відкривається вліво і вправо.
    Малюнок 11.4.40

    5.

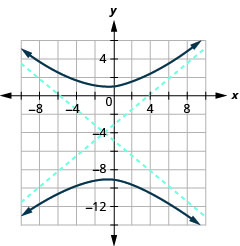
    Графік показує вісь x та вісь y, які обидва проходять у негативному та позитивному напрямках з центром (1, негативним 4) асимптотою, яка проходить через (негативний 7, 1) та (5, негативний 9) та асимптоту, яка проходить через (5, 1) та (негативний 7, негативний 9), та гілки, що проходять через вершини (1, 1) і (1, негативні 9) і відкриваються вгору і вниз.
    Малюнок 11.4.41

    7.

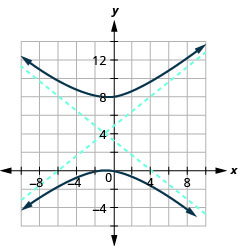
    Графік показує вісь x та вісь y, які обидва проходять у негативному та позитивному напрямках з центром (негативним 1, 4) асимптотою, яка проходить через (4, 8) та (негативний 6, 0) та асимптоту, яка проходить через (негативні 6, 8) та (4, 0) та гілки, що проходять через вершини (негативні 1, 0) та ( негативні 1, 8) і відкриваються вгору і вниз.
    Малюнок 11.4.42

    9.

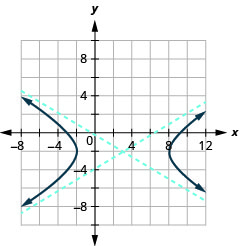
    Графік показує вісь x та вісь y, які обидва проходять у негативному та позитивному напрямках з центром (3, негативним 2) асимптотою, яка проходить через (8, 1) та (негативний 2, негативний 5) та асимптоту, яка проходить через (негативний 2, негативний 1) та (8, негативний 5), та гілки, які проходять через вершини (від'ємні 2, від'ємні 2) і (8, негативні 2) і відкривається вліво і вправо.
    Малюнок 11.4.43
    Вправа\(\PageIndex{15}\) Graph a Hyperbola with Center at \((h,k)\)

    У наступних вправах,

    1. Запишіть рівняння в стандартному вигляді і
    2. Графік.
    1. \(9 x^{2}-4 y^{2}-18 x+8 y-31=0\)
    2. \(16 x^{2}-4 y^{2}+64 x-24 y-36=0\)
    3. \(y^{2}-x^{2}-4 y+2 x-6=0\)
    4. \(4 y^{2}-16 x^{2}-24 y+96 x-172=0\)
    5. \(9 y^{2}-x^{2}+18 y-4 x-4=0\)
    Відповідь

    1.

    1. \(\frac{(x-1)^{2}}{4}-\frac{(y-1)^{2}}{9}=1\)
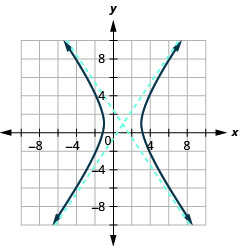
    Графік показує вісь x та вісь y, які обидва проходять у негативному та позитивному напрямках з центром (1, 1) асимптотою, яка проходить через (3, 4) та (негативний 1, негативний 2) та асимптоту, яка проходить через (негативний 1, 4) та (3, негативний 2), та гілки, що проходять через вершини (негативний 1, 1) і (3, 1) і відкривається вліво і вправо.
    Малюнок 11.4.44

    3.

    1. \(\frac{(y-2)^{2}}{9}-\frac{(x-1)^{2}}{9}=1\)
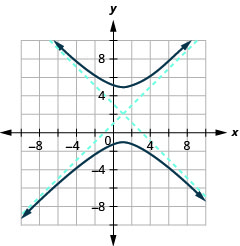
    Графік показує вісь x та вісь y, які обидва проходять у негативному та позитивному напрямках з центром (1, 2) асимптотою, яка проходить через (4, 5) та (негативний 2, негативний 1) та асимптоту, яка проходить через (негативний 2, 5) та (4, негативний 1), та гілки, що проходять через вершини (1, 5) та ( 1, негативний 1) і відкрити вгору і вниз.
    Малюнок 11.4.45

    5.

    1. \(\frac{(y+1)^{2}}{1}-\frac{(x+2)^{2}}{9}=1\)
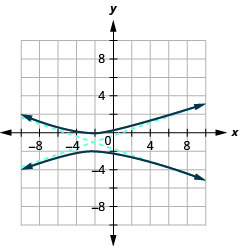
    Графік показує вісь x та вісь y, які обидва проходять у негативному та позитивному напрямках з центром (негативний 2, негативний 1) асимптотою, яка проходить через (1, 0) та (негативний 5, негативний 2) та асимптоту, яка проходить через (3, 0) та (1, негативний 2), та гілки, що проходять через вершини ( негативні 2, 0) і (негативні 2, негативні 2) і відкриваються вгору і вниз.
    Малюнок 11.4.46
    Вправа\(\PageIndex{16}\) Identify the Graph of each Equation as a Circle, Parabola, Ellipse, or Hyperbola

    У наступних вправах визначте тип графіка.

      1. \(x=-y^{2}-2 y+3\)
      2. \(9 y^{2}-x^{2}+18 y-4 x-4=0\)
      3. \(9 x^{2}+25 y^{2}=225\)
      4. \(x^{2}+y^{2}-4 x+10 y-7=0\)
      1. \(x=-2 y^{2}-12 y-16\)
      2. \(x^{2}+y^{2}=9\)
      3. \(16 x^{2}-4 y^{2}+64 x-24 y-36=0\)
      4. \(16 x^{2}+36 y^{2}=576\)
    Відповідь

    2.

    1. Парабола
    2. Коло
    3. Гіпербола
    4. Еліпс
    Вправа\(\PageIndex{17}\) Mixed Practice

    У наступних вправах проведіть графік кожного рівняння.

    1. \(\frac{(y-3)^{2}}{9}-\frac{(x+2)^{2}}{16}=1\)
    2. \(x^{2}+y^{2}-4 x+10 y-7=0\)
    3. \(y=(x-1)^{2}+2\)
    4. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    5. \((x+2)^{2}+(y-5)^{2}=4\)
    6. \(9 x^{2}-4 y^{2}+54 x+8 y+41=0\)
    7. \(x=-y^{2}-2 y+3\)
    8. \(16 x^{2}+9 y^{2}=144\)
    Відповідь

    2.

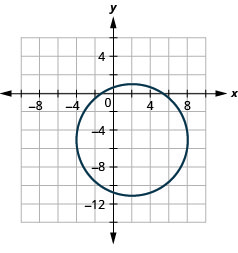
    Графік показує координатну площину x y з колом, центр якого (2, від'ємний 5) і радіус якого 6 одиниць.
    Малюнок 11.4.47

    4.

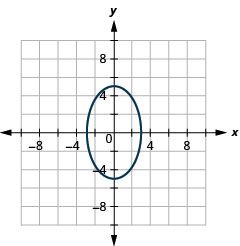
    Графік показує координатну площину x y з еліпсом, велика вісь якого вертикальна, вершини (0, плюс або мінус 5) і спів-вершини (плюс або мінус 3, 0).
    Малюнок 11.4.48

    6.

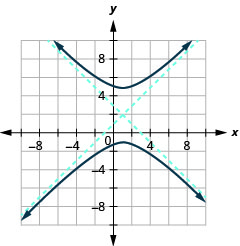
    Графік показує координатну площину x y з центром (1, 2) асимптотою, яка проходить через (негативний 2, 5) і (5, негативний 1) і асимптоту, яка проходить через (4, 5) і (2, 0), і гілки, які проходять через вершини (1, 5) і (негативні 2, негативні 1) і відкриваються вгору і вниз.
    Малюнок 11.4.49

    8.

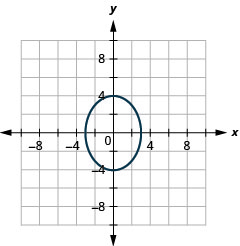
    Графік показує координатну площину x y з еліпсом, велика вісь якого вертикальна, вершини (0, плюс або мінус 4) і спів-вершини (плюс або мінус 3, 0).
    Малюнок 11.4.50
    Вправа\(\PageIndex{18}\) Writing Exercises
    1. Своїми словами визначте гіперболу і запишіть рівняння гіперболи, зосередженої на початку, в стандартній формі. Намалюйте ескіз гіперболи, що позначає центр, вершини та асимптоти.
    2. Поясніть своїми словами, як створити та використовувати прямокутник, який допомагає графіку гіперболи.
    3. Порівняйте і порівняйте графіки рівнянь\(\frac{x^{2}}{4}-\frac{y^{2}}{9}=1\) і\(\frac{y^{2}}{9}-\frac{x^{2}}{4}=1\).
    4. Поясніть своїми словами, як відрізнити рівняння еліпса з рівнянням гіперболи.
    Відповідь

    2. Відповіді можуть відрізнятися

    4. Відповіді можуть відрізнятися

    Самостійна перевірка

    а Після виконання вправ використовуйте цей контрольний список, щоб оцінити своє володіння цілями цього розділу.

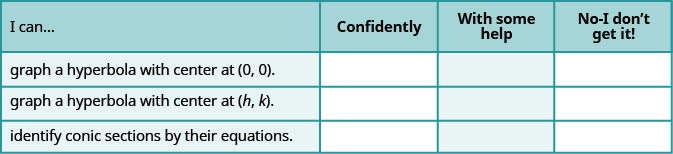
    Ця таблиця складається з чотирьох стовпців і чотирьох рядків. Перший рядок є заголовком, і він позначає кожен стовпець, â € œi canâ€â€, “впевнено, â€ â€ â€œЗ деякою допомогою, †і “no-i don’ t отримати його! â € У рядку 2, я можу був граф гіпербола з центром в (0, 0). У рядку 3 я можу був граф гіпербола з центром в (h, k). У рядку 4 я можу ідентифікувати конічні перерізи за їх рівняннями.
    Малюнок 11.4.51

    б За шкалою 1-10, як би ви оцінили своє володіння цим розділом у світлі ваших відповідей на контрольний список? Як ви можете це покращити?