Skip to main content
LibreTexts - Ukrayinska

11.3E: Вправи

  1. Last updated
  2. Save as PDF
  • Page ID
    59805

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Практика робить досконалим

    Вправа\(\PageIndex{17}\) Graph Vertical Parabolas

    У наступних вправах складіть графік кожного рівняння за допомогою властивостей.

    1. \(y=-x^{2}+4 x-3\)
    2. \(y=-x^{2}+8 x-15\)
    3. \(y=6 x^{2}+2 x-1\)
    4. \(y=8 x^{2}-10 x+3\)
    Відповідь

    1.

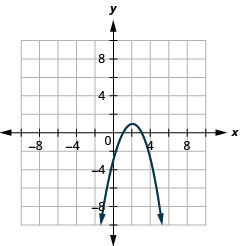
    Цей графік показує параболу, що відкривається вниз з вершиною (2, 1) та x перехопленнями (1, 0) та (3, 0).
    Малюнок 11.2.83

    3.

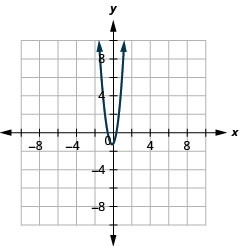
    Цей графік показує параболу, що відкривається вгору. Вершина дорівнює (від'ємний 0.167, негативний 1.167), x перехоплює (від'ємний 0.608) і (від'ємний 0.274, 0), а y-перехоплення - (0, негативний 1).
    Малюнок 11.2.84
    Вправа\(\PageIndex{18}\) Graph Vertical Parabolas

    У наступних вправах,

    1. Запишіть рівняння в стандартному вигляді і
    2. Використовуйте властивості стандартної форми для побудови графіка рівняння.
    1. \(y=-x^{2}+2 x-4\)
    2. \(y=2 x^{2}+4 x+6\)
    3. \(y=-2 x^{2}-4 x-5\)
    4. \(y=3 x^{2}-12 x+7\)
    Відповідь

    1.

    1. \(y=-(x-1)^{2}-3\)
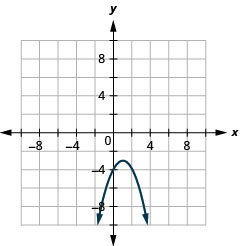
    Цей графік показує параболу, що відкривається вниз з вершиною (1, негативним 3) та перехопленням y (0, 4).
    Малюнок 11.2.85

    3.

    1. \(y=-2(x+1)^{2}-3\)
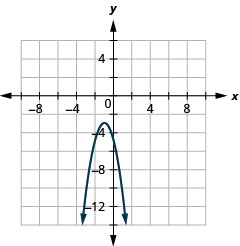
    Цей графік показує параболу, що відкривається вниз з вершиною (від'ємний 1, від'ємний 3) та x перехоплює (від'ємний 5, 0).
    Малюнок 11.2.86
    Вправа\(\PageIndex{19}\) Graph Horizontal Parabolas

    У наступних вправах складіть графік кожного рівняння за допомогою властивостей.

    1. \(x=-2 y^{2}\)
    2. \(x=3 y^{2}\)
    3. \(x=4 y^{2}\)
    4. \(x=-4 y^{2}\)
    5. \(x=-y^{2}-2 y+3\)
    6. \(x=-y^{2}-4 y+5\)
    7. \(x=y^{2}+6 y+8\)
    8. \(x=y^{2}-4 y-12\)
    9. \(x=(y-2)^{2}+3\)
    10. \(x=(y-1)^{2}+4\)
    11. \(x=-(y-1)^{2}+2\)
    12. \(x=-(y-4)^{2}+3\)
    13. \(x=(y+2)^{2}+1\)
    14. \(x=(y+1)^{2}+2\)
    15. \(x=-(y+3)^{2}+2\)
    16. \(x=-(y+4)^{2}+3\)
    17. \(x=-3(y-2)^{2}+3\)
    18. \(x=-2(y-1)^{2}+2\)
    19. \(x=4(y+1)^{2}-4\)
    20. \(x=2(y+4)^{2}-2\)
    Відповідь

    1.

    Цей графік показує параболу, що відкривається ліворуч з вершиною (0, 0). Два пункти на ньому - (негативний 2, 1) і (негативний 2, негативний 1).
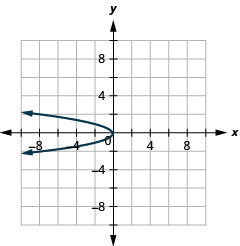
    Малюнок 11.2.87

    3.

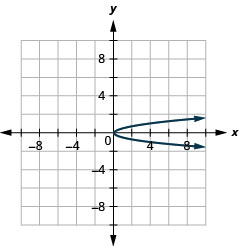
    Цей графік показує параболу, що відкривається праворуч з вершиною (0, 0). Дві точки на ньому - (4, 1) і (4, негативні 1).
    Малюнок 11.2.88

    5.

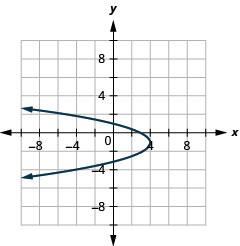
    Цей графік показує параболу, що відкривається ліворуч з вершиною (4, від'ємною 1) та y перехопленнями (0, 1) та (0, негативними 3).
    Малюнок 11.2.89

    7.

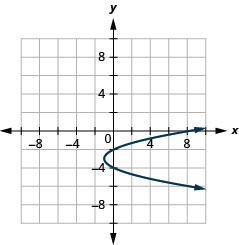
    Цей графік показує параболу, що відкривається праворуч з вершиною (від'ємний 1, негативний 3) і y перехоплює (0, негативний 2) і (0, негативний 4).
    Малюнок 11.2.90

    9.

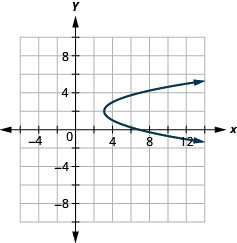
    Цей графік показує параболу, що відкривається праворуч з вершиною (3, 2) та перехопленням x (7, 0).
    Малюнок 11.2.91

    11.

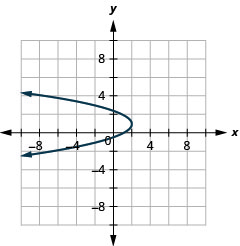
    Цей графік показує параболу, що відкривається ліворуч з вершиною (2, 1) та перехопленням x (1, 0).
    Малюнок 11.2.92

    13.

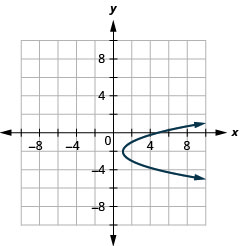
    Цей графік показує параболу, що відкривається праворуч з вершиною (1, від'ємною 2) та перехопленням x (5, 0).
    Малюнок 11.2.93

    15.

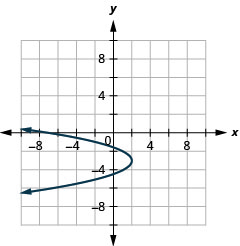
    Цей графік показує параболу, що відкривається ліворуч з вершиною (2, від'ємна 3). Дві точки на ньому є (негативний 2, негативний 1) і (негативний 2, 5).
    Малюнок 11.2.94

    17.

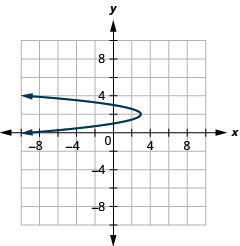
    Цей графік показує параболу, що відкривається ліворуч з вершиною (3, 2) та y перехопленнями (0, 1) та (0, 3).
    Малюнок 11.2.95

    19.

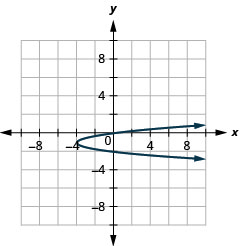
    Цей графік показує параболу, що відкривається праворуч з вершиною (від'ємний 4, від'ємний 1) та y перехоплює (0, 0) та (0, негативний 2).
    Малюнок 11.2.96
    Вправа\(\PageIndex{20}\) Graph Horizontal Parabolas

    У наступних вправах,

    1. Запишіть рівняння в стандартному вигляді і
    2. Використовуйте властивості стандартної форми для побудови графіка рівняння.
    1. \(x=y^{2}+4 y-5\)
    2. \(x=y^{2}+2 y-3\)
    3. \(x=-2 y^{2}-12 y-16\)
    4. \(x=-3 y^{2}-6 y-5\)
    Відповідь

    1.

    1. \(x=(y+2)^{2}-9\)
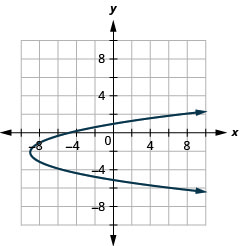
    Цей графік показує параболу, що відкривається праворуч з вершиною (від'ємний 9, від'ємний 2) і y перехоплює (0, 1) і (0, негативний 5).
    Малюнок 11.2.97

    3.

    1. \(x=-2(y+3)^{2}+2\)
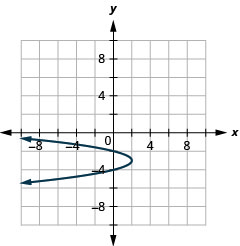
    Цей графік показує параболу, що відкривається ліворуч з вершиною (2, від'ємною 3) та y перехопленнями (0, негативною 2) та (0, негативною 4).
    Малюнок 11.2.98
    Вправа\(\PageIndex{21}\) Mixed Practice

    У наступних вправах зіставте кожен графік до одного з наступних рівнянь:

    1. \(x^{2}+y^{2}=64\)
    2. \(x^{2}+y^{2}=49\)
    3. \((x+5)^{2}+(y+2)^{2}=4\)
    4. \((x-2)^{2}+(y-3)^{2}=9\)
    5. \(y=-x^{2}+8 x-15\)
    6. \(y=6 x^{2}+2 x-1\)

    1.

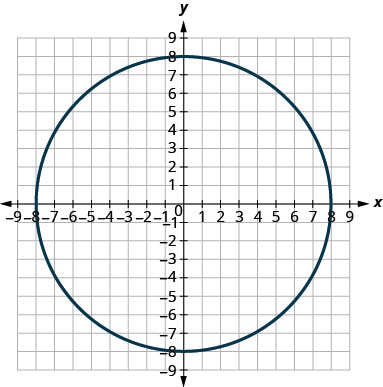
    Цей графік показує коло з центром (0, 0) і радіусом 8 одиниць.
    Малюнок 11.2.99

    2.

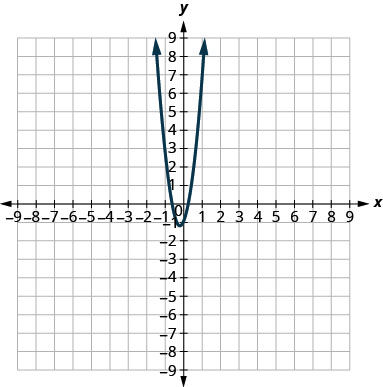
    Цей графік показує параболу, що відкривається вгору. Його вершина має значення x трохи менше 0 і значення y трохи менше від'ємного 1. Точка на ній близька до (негативна 1, 3).
    Малюнок 11.2.100

    3.

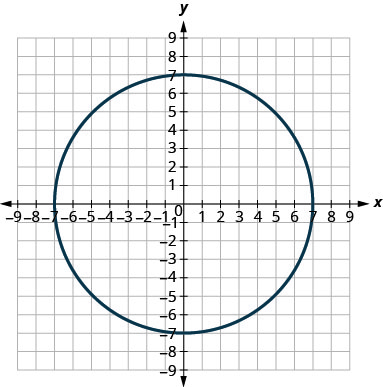
    Цей графік показує коло з центром (0, 0) і радіусом 7 одиниць.
    Малюнок 11.2.101

    4.

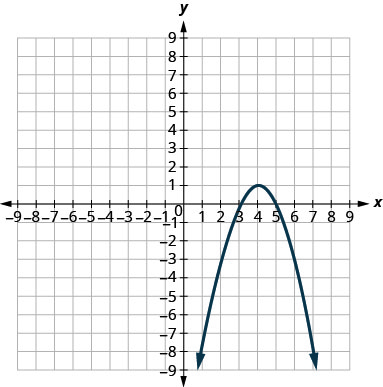
    Цей графік показує параболу, що відкривається вниз з вершиною (4, 1) та x перехопленнями (3, 0) та (5, 0).
    Малюнок 11.2.102

    5.

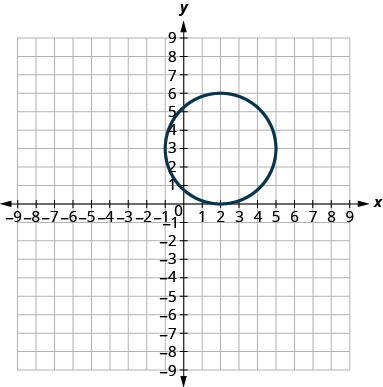
    Цей графік показує коло з центром (2, 3) і радіусом 3 одиниці.
    Малюнок 11.2.103

    6.

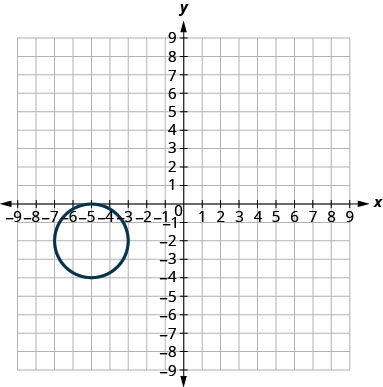
    Цей графік показує коло з центром (від'ємний 5, від'ємний 2) і радіусом 2 одиниці.
    Малюнок 11.2.104
    Відповідь

    1. а

    3. б

    5. д

    Вправа\(\PageIndex{22}\) Solve Applications with Parabolas

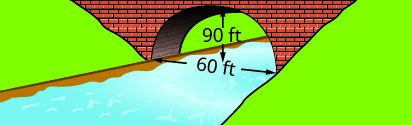
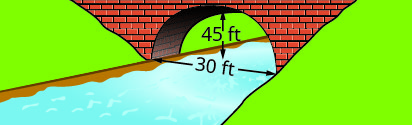
    Запишіть рівняння в стандартній формі параболічної арки, утвореної в фундаменті показаного моста. Використовуйте нижню ліву частину моста як початок\((0, 0)\).

    1.

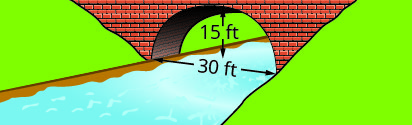
    Цей графік показує коло з центром (від'ємний 5, від'ємний 2) і радіусом 2 одиниці.
    Малюнок 11.2.105

    2.

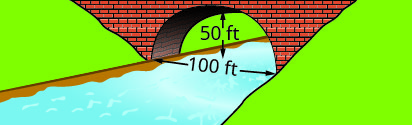
    На цьому малюнку зображена параболічна арка, утворена в фундаменті моста. Це 50 футів у висоту і 100 футів в ширину біля основи.
    Малюнок 11.2.106

    3.

    На цьому малюнку зображена параболічна арка, утворена в фундаменті моста. Це 90 футів у висоту і 60 футів в ширину біля основи.
    Малюнок 11.2.107

    4.

    На цьому малюнку зображена параболічна арка, утворена в фундаменті моста. Це 45 футів у висоту і 30 футів в ширину біля основи.
    Малюнок 11.2.108
    Відповідь

    1. \(y=-\frac{1}{15}(x-15)^{2}+15\)

    3. \(y=-\frac{1}{10}(x-30)^{2}+90\)

    Вправа\(\PageIndex{23}\) Writing Exercises
    1. Своїми словами визначте параболу.
    2. Чи є\(y=x^{2}\) парабола функцією? Чи є\(x=y^{2}\) парабола функцією? Поясніть, чому чи чому ні.
    3. Напишіть рівняння параболи, що відкривається вгору або вниз у стандартній формі, і рівняння параболи, що відкривається вліво або вправо в стандартній формі. Надайте ескіз параболи для кожної з них, позначте вершину і вісь симетрії.
    4. Поясніть своїми словами, як ви можете визначити з його рівняння, чи відкривається парабола вгору, вниз, вліво чи вправо.
    Відповідь

    1. Відповіді можуть відрізнятися

    3. Відповіді можуть відрізнятися

    Самостійна перевірка

    а Після виконання вправ скористайтеся цим контрольним списком, щоб оцінити своє володіння цілями цього розділу.

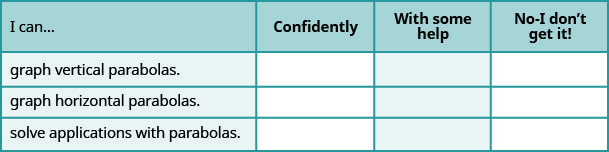
    Ця таблиця має чотири стовпці, 3 рядки та рядок заголовка. Рядок заголовка позначає кожен стовпець, який я можу, впевнено, з деякою допомогою і ні, я не можу отримати його™. Перший стовпець має такі твердження: граф вертикальних парабол, граф горизонтальних парабол, розв'язування додатків з параболами. Решта стовпці порожні.
    Малюнок 11.2.109

    б Ознайомившись з цим контрольним списком, що ви будете робити, щоб стати впевненими у всіх цілях?