6.5: Загальна стратегія факторингу поліноміальних виразів
- Page ID
- 59540
До кінця цього розділу ви зможете:
- Розпізнайте та використовуйте відповідний метод для повного множника
Розпізнайте та використовуйте відповідний метод для повного фактору полінома
Ви зараз ознайомилися з усіма методами факторингу, які вам знадобляться в даному курсі. Наступна діаграма узагальнює всі методи факторингу, які ми розглянули, та окреслює стратегію, яку слід використовувати при факторингу поліномів.

- Чи існує найбільший загальний фактор?
Фактор це поза. - Поліном є біноміальним, триноміальним, або існує більше трьох членів?
Якщо це біном:- Це сума?
З квадратів? Суми квадратів не коефіцієнт.
З кубиків? Використовуйте шаблон суми кубиків. - Це різниця?
З квадратів? Фактор як добуток кон'югатів.
З кубиків? Скористайтеся різницею кубиків візерунком.
- Це форми\(x^2+bx+c\)? Скасувати фольгу.
- Це форми\(ax^2+bx+c\)?
Якщо a і c є квадратами, перевірте, чи відповідає він триноміальному квадратному візерунку.
Використовуйте метод проб і помилок або «\(ac\)».
- Скористайтеся методом групування.
- Це сума?
- Перевірка.
Чи враХОвано це повністю?
Чи множиться множник до початкового многочлена?
Пам'ятайте, поліном повністю враховується, якщо, крім мономів, його фактори прості!
Фактор повністю:\(7x^3−21x^2−70x\).
Рішення
\(\begin{array} {ll} {7x^3−21x^2−70x} & \\ \text{Is there a GCF? Yes, }7x. & \\ \text{Factor out the GCF.} &7x(x^2−3x−10) \\ \text{In the parentheses, is it a binomial, trinomial,} & \\ \text{or are there more terms?} & \\ \text{Trinomial with leading coefficient 1.} & \\ \text{“Undo” FOIL.} &7x(x\hspace{8mm})(x\hspace{8mm}) \\ &7x(x+2)(x−5) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Neither binomial can be factored.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ & \\ & \\ \hspace{15mm}7x(x+2)(x−5) & \\ \hspace{10mm}7x(x^2−5x+2x−10) & \\ \hspace{15mm}7x(x^2−3x−10) & \\ \hspace{13mm}7x^3−21x^2−70x\checkmark & \end{array} \)
Фактор повністю:\(8y^3+16y^2−24y\).
- Відповідь
-
\(8y(y−1)(y+3)\)
Фактор повністю:\(5y^3−15y^2−270y\).
- Відповідь
-
\(5y(y−9)(y+6)\)
Будьте обережні, коли вас просять фактор біноміального, оскільки є кілька варіантів!
Фактор повністю:\(24y^2−150\)
Рішення
\(\begin{array} {ll} &24y^2−150 \\ \text{Is there a GCF? Yes, }6. & \\ \text{Factor out the GCF.} &6(4y^2−25) \\ \text{In the parentheses, is it a binomial, trinomial} & \\ \text{or are there more than three terms? Binomial.} & \\ \text{Is it a sum? No.} & \\ \text{Is it a difference? Of squares or cubes? Yes, squares.} &6((2y)^2−(5)^2) \\ \text{Write as a product of conjugates.} &6(2y−5)(2y+5) \\ & \\ & \\ \hspace{5mm}\text{Is the expression factored completely?} & \\ \hspace{5mm}\text{Neither binomial can be factored.} & \\ \text{Check:} & \\ & \\ & \\ \hspace{5mm}\text{Multiply.} & \\ & \\ \hspace{15mm}6(2y−5)(2y+5) & \\ & \\ \hspace{18mm}6(4y^2−25) & \\ \hspace{18mm}24y^2−150\checkmark \end{array}\)
Фактор повністю:\(16x^3−36x\).
- Відповідь
-
\(4x(2x−3)(2x+3)\)
Фактор повністю:\(27y^2−48\).
- Відповідь
-
\(3(3y−4)(3y+4)\)
Наступний приклад можна врахувати за допомогою декількох методів. Розпізнавання візерунка триноміальних квадратів полегшить вашу роботу.
Фактор повністю:\(4a^2−12ab+9b^2\).
Рішення
\(\begin{array} {ll} &4a^2−12ab+9b^2 \\ \text{Is there a GCF? No.} & \\ \text{Is it a binomial, trinomial, or are there more terms?} & \\ \text{Trinomial with }a\neq 1.\text{ But the first term is a perfect square.} \\ \text{Is the last term a perfect square? Yes.} &(2a)^2−12ab+(3b)^2 \\ \text{Does it fit the pattern, }a^2−2ab+b^2?\text{ Yes.} &(2a)^2 −12ab+ (3b)^2 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(2a)(3b)}{\,}^{\swarrow}\\ \text{Write it as a square.} &(2a−3b)^2 \\ & \\ & \\ \quad\text{Is the expression factored completely? Yes.} & \\ \quad\text{The binomial cannot be factored.} & \\ \text{Check your answer.} \\ & \\ & \\ \quad\text{Multiply.} & \\ \hspace{30mm}(2a−3b)^2 \\ \hspace{20mm} (2a)^2−2·2a·3b+(3b)^2 \\ \hspace{24mm}4a^2−12ab+9b^2\checkmark & \end{array} \)
Фактор повністю:\(4x^2+20xy+25y^2\).
- Відповідь
-
\((2x+5y)^2\)
Фактор повністю:\(9x^2−24xy+16y^2\).
- Відповідь
-
\((3x−4y)^2\)
Пам'ятайте, суми квадратів не коефіцієнт, але суми кубів роблять!
Фактор повністю\(12x^3y^2+75xy^2\).
Рішення
\(\begin{array} {ll} &12x^3y^2+75xy^2 \\ \text{Is there a GCF? Yes, }3xy^2. & \\ \text{Factor out the GCF.} &3xy^2(4x^2+25) \\ \text{In the parentheses, is it a binomial, trinomial, or are} & \\ \text{there more than three terms? Binomial.} & \\ & \\ \text{Is it a sum? Of squares? Yes.} &\text{Sums of squares are prime.} \\ & \\ & \\ \quad\text{Is the expression factored completely? Yes.} & \\ \text{Check:} & \\ & \\ & \\ \quad\text{Multiply.} & \\ \hspace{15mm}3xy^2(4x^2+25) & \\ \hspace{14mm}12x^3y^2+75xy^2\checkmark \end{array} \)
Фактор повністю:\(50x^3y+72xy\).
- Відповідь
-
\(2xy(25x^2+36)\)
Фактор повністю:\(27xy^3+48xy\).
- Відповідь
-
\(3xy(9y^2+16)\)
При використанні суми або різниці кубиків візерунком, будьте обережні зі знаками.
Фактор повністю:\(24x^3+81y^3\).
Рішення
| Чи є GCF? Так, 3. | 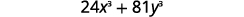 |
| Фактор це. | 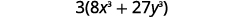 |
| У дужках це біноміальне, триноміальне, чи існує більше трьох членів? Біноміальний. |
|
| Це сума чи різниця? Сума. | |
| З квадратів або кубиків? Сума кубів. | 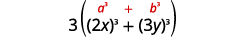 |
| Напишіть його, використовуючи шаблон суми кубиків. | 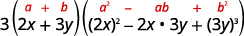 |
| Чи повністю враХОвано вираз? Так. | 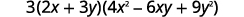 |
| Перевірка шляхом множення. |
Фактор повністю:\(250m^3+432n^3\).
- Відповідь
-
\(2(5m+6n)(25m^2−30mn+36n^2)\)
Фактор повністю:\(2p^3+54q^3\).
- Відповідь
-
\(2(p+3q)(p^2−3pq+9q^2)\)
Фактор повністю:\(3x^5y−48xy\).
Рішення
\(\begin{array} {ll} &3x^5y−48xy \\ \text{Is there a GCF? Factor out }3xy &3xy(x^4−16) \\ \begin{array} {l} \text{Is the binomial a sum or difference? Of squares or cubes?} \\ \text{Write it as a difference of squares.} \end{array} &3xy\left((x^2)^2−(4)2\right) \\ \text{Factor it as a product of conjugates} &3xy(x^2−4)(x^2+4) \\ \text{The first binomial is again a difference of squares.} &3xy\left((x)^2−(2)^2\right)(x^2+4) \\ \text{Factor it as a product of conjugates.} &3xy(x−2)(x+2)(x^2+4) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ 3xy(x−2)(x+2)(x^2+4) & \\ 3xy(x^2−4)(x^2+4) & \\ 3xy(x^4−16) & \\ 3x^5y−48xy\checkmark & \end{array}\)
Фактор повністю:\(4a^5b−64ab\).
- Відповідь
-
\(4ab(a^2+4)(a−2)(a+2)\)
Фактор повністю:\(7xy^5−7xy\).
- Відповідь
-
\(7xy(y^2+1)(y−1)(y+1)\)
Фактор повністю:\(4x^2+8bx−4ax−8ab\).
Рішення
\(\begin{array} {ll} &4x^2+8bx−4ax−8ab \\ \text{Is there a GCF? Factor out the GCF, }4. &4(x^2+2bx−ax−2ab) \\ \text{There are four terms. Use grouping.} &4[x(x+2b)−a(x+2b)]4(x+2b)(x−a) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{25mm}4(x+2b)(x−a) & \\ \hspace{20mm} 4(x^2−ax+2bx−2ab) & \\ \hspace{20mm}4x^2+8bx−4ax−8ab\checkmark \end{array}\)
Фактор повністю:\(6x^2−12xc+6bx−12bc\).
- Відповідь
-
\(6(x+b)(x−2c)\)
Фактор повністю:\(16x^2+24xy−4x−6y\).
- Відповідь
-
\(2(4x−1)(2x+3y)\)
Виймаючи повний GCF на першому кроці, завжди полегшить вашу роботу.
Фактор повністю:\(40x^2y+44xy−24y\).
Рішення
\(\begin{array} {ll} &40x^2y+44xy−24y \\ \text{Is there a GCF? Factor out the GCF, }4y. &4y(10x^2+11x−6) \\ \text{Factor the trinomial with }a\neq 1. &4y(10x^2+11x−6) \\ &4y(5x−2)(2x+3) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{25mm}4y(5x−2)(2x+3) & \\ \hspace{24mm}4y(10x^2+11x−6) & \\ \hspace{22mm}40x^2y+44xy−24y\checkmark \end{array}\)
Фактор повністю:\(4p^2q−16pq+12q\).
- Відповідь
-
\(4q(p−3)(p−1)\)
Фактор повністю:\(6pq^2−9pq−6p\).
- Відповідь
-
\(3p(2q+1)(q−2)\)
Коли ми перерахували многочлен з чотирма долями, найчастіше ми розділили його на дві групи з двох членів. Пам'ятайте, що ми також можемо розділити його на тріноміал, а потім один термін.
Фактор повністю:\(9x^2−12xy+4y^2−49\).
Рішення
\(\begin{array} {ll} &9x^2−12xy+4y^2−49 \\ \text{Is there a GCF? No.} & \\ \begin{array} {l} \text{With more than 3 terms, use grouping. Last 2 terms} \\ \text{have no GCF. Try grouping first 3 terms.} \end{array} &9x^2−12xy+4y^2−49 \\ \begin{array} {l} \text{Factor the trinomial with }a\neq 1. \text{ But the first term is a} \\ \text{perfect square.} \end{array} & \\ \text{Is the last term of the trinomial a perfect square? Yes.} &(3x)^2−12xy+(2y)^2−49 \\ \text{Does the trinomial fit the pattern, }a^2−2ab+b^2? \text{ Yes.} &(3x)^2 −12xy+ (2y)^2−49 \\ &\hspace{7mm} {\,}^{\searrow}{\,}_{−2(3x)(2y))}{\,}^{\swarrow} \\ \text{Write the trinomial as a square.} &(3x−2y)^2−49 \\ \begin{array} {ll} \text{Is this binomial a sum or difference? Of squares or} \\ \text{cubes? Write it as a difference of squares.} \end{array} &(3x−2y)^2−72 \\ \text{Write it as a product of conjugates.} &((3x−2y)−7)((3x−2y)+7) \\ &(3x−2y−7)(3x−2y+7) \\ \text{Is the expression factored completely? Yes.} & \\ \text{Check your answer.} & \\ \text{Multiply.} & \\ \hspace{23mm}(3x−2y−7)(3x−2y+7) & \\ \hspace{10mm}9x^2−6xy−21x−6xy+4y^2+14y+21x−14y−49 \qquad & \\ \hspace{25mm}9x^2−12xy+4y^2−49\checkmark & \end{array}\)
Фактор повністю:\(4x^2−12xy+9y^2−25\).
- Відповідь
-
\((2x−3y−5)(2x−3y+5)\)
Фактор повністю:\(16x^2−24xy+9y^2−64\).
- Відповідь
-
\((4x−3y−8)(4x−3y+8)\)
Ключові поняття

- Як використовувати загальну стратегію факторингу поліномів.
- Чи існує найбільший загальний фактор?
Фактор це поза. - Поліном є біноміальним, триноміальним, або існує більше трьох членів?
Якщо це біном:
це сума?
З квадратів? Суми квадратів не коефіцієнт.
З кубиків? Використовуйте шаблон суми кубиків.
Це різниця?
З квадратів? Фактор як добуток кон'югатів.
З кубиків? Скористайтеся різницею кубиків візерунком.
Якщо це триноміал:
це форма\(x^2+bx+c\)? Скасувати фольгу.
Це форми\(ax^2+bx+c\)?
Якщо a і c є квадратами, перевірте, чи відповідає він триноміальному квадратному візерунку.
Використовуйте метод проб і помилок або «\(ac\)».
Якщо він містить більше трьох термінів:
скористайтеся методом групування. - Перевірка.
Чи враХОвано це повністю?
Чи множиться множник до початкового многочлена?
- Чи існує найбільший загальний фактор?
