6.6: Поліноміальні рівняння
- Page ID
- 59562
До кінця цього розділу ви зможете:
- Використовувати властивість нульового продукту
- Розв'язувати квадратні рівняння методом факторингу
- Розв'язуйте рівняння з поліноміальними функціями
- Розв'язуйте програми, змодельовані поліноміальними рівняннями
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Вирішити:\(5y−3=0\).
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Фактор повністю:\(n^3−9n^2−22n\).
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Якщо\(f(x)=8x−16\), знайдіть\(f(3)\) і вирішуйте\(f(x)=0\).
Якщо ви пропустили цю проблему, перегляньте [посилання].
Ми витратили значний час на те, щоб навчитися фактору поліномів. Зараз ми розглянемо поліноміальні рівняння і вирішимо їх за допомогою факторингу, якщо це можливо.
Поліноміальне рівняння - це рівняння, яке містить поліноміальний вираз. Ступінь рівняння полінома - це ступінь многочлена.
Поліноміальне рівняння - це рівняння, яке містить поліноміальний вираз.
Ступінь рівняння полінома - це ступінь многочлена.
Ми вже розв'язали поліноміальні рівняння першого ступеня. Поліноміальні рівняння першого ступеня є лінійними рівняннями виду\(ax+b=c\).
Зараз ми будемо вирішувати поліноміальні рівняння другого ступеня. Поліноміальне рівняння другого ступеня називається квадратним рівнянням. Нижче наведено кілька прикладів квадратичних рівнянь:
\[x^2+5x+6=0 \qquad 3y^2+4y=10 \qquad 64u^2−81=0 \qquad n(n+1)=42 \nonumber\]
Останнє рівняння, здається, не має змінної в квадраті, але коли ми спростимо вираз зліва, ми отримаємо\(n^2+n\).
Загальна форма квадратного рівняння -\(ax^2+bx+c=0\), с\(a\neq 0\). (Якщо\(a=0\), то\(0·x^2=0\) і у нас залишилося без квадратичного терміну.)
Рівняння виду\(ax^2+bx+c=0\) називається квадратним рівнянням.
\[a,b,\text{ and }c\text{ are real numbers and }a\neq 0\nonumber\]
Для розв'язання квадратичних рівнянь потрібні методи, відмінні від тих, які ми використовували при розв'язанні лінійних рівнянь. Ми розглянемо один метод тут, а потім кілька інших в наступному розділі.
Використовувати властивість нульового продукту
Спочатку ми вирішимо деякі квадратні рівняння за допомогою властивості нульового продукту. Властивість нульового продукту говорить, що якщо добуток двох величин дорівнює нулю, то хоча б одна з величин дорівнює нулю. Єдиний спосіб отримати добуток, рівний нулю - помножити на сам нуль.
Якщо\(a·b=0\), то або або\(a=0\)\(b=0\) або і те, і інше.
Тепер ми будемо використовувати властивість нульового продукту, щоб вирішити квадратне рівняння.
Вирішити:\((5n−2)(6n−1)=0\).
- Відповідь
-



Вирішити:\((3m−2)(2m+1)=0\).
- Відповідь
-
\(m=\frac{2}{3},\space m=−\frac{1}{2}\)
Вирішити:\((4p+3)(4p−3)=0\).
- Відповідь
-
\(p=−\frac{3}{4},\space p=\frac{3}{4}\)
- Встановіть кожен коефіцієнт рівним нулю.
- Розв'яжіть лінійні рівняння.
- Перевірте.
Розв'язування квадратних рівнянь методом факторингу
Властивість нульового продукту працює дуже добре для вирішення квадратних рівнянь. Квадратне рівняння має бути враховано, з нулем, ізольованим з одного боку. Тому ми обов'язково почнемо з квадратного рівняння в стандартній формі,\(ax^2+bx+c=0\). Потім фактуємо вираз зліва.
Вирішити:\(2y^2=13y+45\).
- Відповідь
-

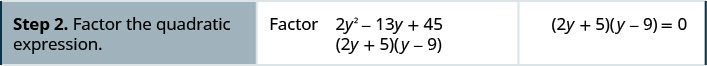


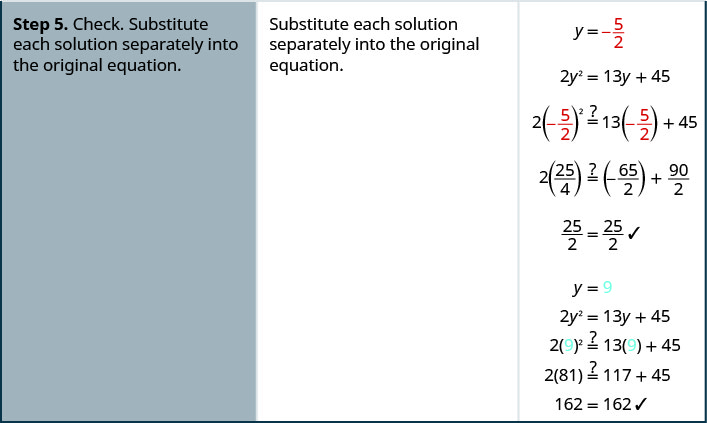
Вирішити:\(3c^2=10c−8\).
- Відповідь
-
\(c=2,\space c=\frac{4}{3}\)
Вирішити:\(2d^2−5d=3\).
- Відповідь
-
\(d=3,\space d=−12\)
- Запишіть квадратне рівняння в стандартному вигляді,\(ax^2+bx+c=0\).
- Фактор квадратичного виразу.
- Використовуйте властивість нульового продукту.
- Розв'яжіть лінійні рівняння.
- Перевірте. Підставляємо кожне рішення окремо в вихідне рівняння.
Перш ніж ми зробимо множник, ми повинні переконатися, що квадратне рівняння знаходиться в стандартній формі.
Вирішення квадратних рівнянь шляхом факторингу буде використовувати всі методи факторингу, які ви дізналися в цьому розділі! Чи розпізнаєте ви спеціальний візерунок продукту в наступному прикладі?
Вирішити:\(169q^2=49\).
- Відповідь
-
\(\begin{array} {ll} &169x^2=49 \\ \text{Write the quadratic equation in standard form.} &169x^2−49=0 \\ \text{Factor. It is a difference of squares.} &(13x−7)(13x+7)=0 \\ \text{Use the Zero Product Property to set each factor to }0. & \\ \text{Solve each equation.} &\begin{array} {ll} 13x−7=0 &13x+7=0 \\ 13x=7 &13x=−7 \\ x=\frac{7}{13} &x=−\frac{7}{13} \end{array} \end{array}\)
Перевірка:
Ми залишаємо чек за вами.
Вирішити:\(25p^2=49\).
- Відповідь
-
\(p=\frac{7}{5},p=−\frac{7}{5}\)
Вирішити:\(36x^2=121\).
- Відповідь
-
\(x=\frac{11}{6},x=−\frac{11}{6}\)
У наступному прикладі враховується ліва частина рівняння, а права - не нуль. Для того, щоб використовувати властивість нульового продукту, одна сторона рівняння повинна дорівнювати нулю. Ми помножимо множники, а потім запишемо рівняння в стандартній формі.
Вирішити:\((3x−8)(x−1)=3x\).
- Відповідь
-
\(\begin{array} {ll} &(3x−8)(x−1)=3x \\ \text{Multiply the binomials.} &3x^2−11x+8=3x \\ \text{Write the quadratic equation in standard form.} &3x^2−14x+8=0 \\ \text{Factor the trinomial.} &(3x−2)(x−4)=0 \\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} \end{array} &\begin{array} {ll} 3x−2=0 &x−4=0 \\ 3x=2 &x=4 \\ x=\frac{2}{3} & \end{array} \\ \text{Check your answers.} &\text{The check is left to you.} \end{array}\)
Вирішити:\((2m+1)(m+3)=12m\).
- Відповідь
-
\(m=1,\space m=\frac{3}{2}\)
Вирішити:\((k+1)(k−1)=8\).
- Відповідь
-
\(k=3,\space k=−3\)
У наступному прикладі, коли ми множимо квадратне рівняння, ми отримаємо три множники. Однак перший фактор - це константа. Ми знаємо, що коефіцієнт не може дорівнювати 0.
Вирішити:\(3x^2=12x+63\).
- Відповідь
-
\(\begin{array} {ll} &3x^2=12x+63 \\ \text{Write the quadratic equation in standard form.} &3x^2−12x−63=0 \\ \text{Factor the greatest common factor first.} &3(x^2−4x−21)=0 \\ \text{Factor the trinomial.} &3(x−7)(x+3)=0 \\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} \end{array} &\begin{array} {lll} 3\neq 0 &x−7=0 &x+3=0 \\ 3\neq 0 &x=7 &x=−3 \end{array} \\ \text{Check your answers.} &\text{The check is left to you.} \end{array}\)
Вирішити:\(18a^2−30=−33a\).
- Відповідь
-
\(a=−\frac{5}{2},a=\frac{2}{3}\)
Вирішити:\(123b=−6−60b^2\)
- Відповідь
-
\(b=−2,\space b=−\frac{1}{20}\)
Властивість нульового продукту також застосовується до добутку трьох або більше факторів. Якщо твір дорівнює нулю, хоча б один з факторів повинен дорівнювати нулю. Ми можемо вирішити деякі рівняння ступеня більше двох, використовуючи властивість нульового продукту, так само, як ми розв'язували квадратні рівняння.
Вирішити:\(9m^3+100m=60m^2\)
- Відповідь
-
\(\begin{array} {ll} & 9m^3+100m=60m^2 \\ \text{Bring all the terms to one side so that the other side is zero.} &9m^3−60m^2+100m=0 \\ \text{Factor the greatest common factor first.} &m(9m^2−60m+100)=0 \\ \text{Factor the trinomial.} &m(3m−10)^2=0 \end{array}\\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} &\begin{array} {lll} m=0 &3m−10=0 &{}\\ m=0 &m=\frac{10}{3} & {} \end{array}\\ \text{Check your answers.} &\text{The check is left to you.} \end{array}\)
Вирішити:\(8x^3=24x^2−18x\).
- Відповідь
-
\(x=0,\space x=\frac{3}{2}\)
Вирішити:\(16y^2=32y^3+2y\).
- Відповідь
-
\(y=0,\space y=14\)
Розв'язуйте рівняння з поліноміальними функціями
Оскільки наше вивчення поліноміальних функцій триває, часто буде важливо знати, коли функція матиме певне значення або які точки лежать на графіку функції. Наша робота з власністю Zero Product допоможе нам знайти ці відповіді.
Для функції\(f(x)=x^2+2x−2\),
ⓐ знайти,\(x\) коли\(f(x)=6\)
ⓑ знайти дві точки, які лежать на графіку функції.
- Відповідь
-
ⓐ
\(\begin{array} {ll} &f(x)=x^2+2x−2 \\ \text{Substitute }6\text{ for }f(x). &6=x^2+2x−2 \\ \text{Put the quadratic in standard form.} &x^2+2x−8=0 \\ \text{Factor the trinomial.} &(x+4)(x−2)=0 \\ \begin{array} {l} \text{Use the zero product property.} \\ \text{Solve.} \end{array} &\begin{array} {lll} x+4=0 &\text{or} &x−2=0 \\ x=−4 &\text{or} &x=2 \end{array} \\ \text{Check:} & \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ \begin{array} {lll} \quad &\hspace{3mm} f(x)=x^2+2x−2 &f(x)=x^2+2x−2 \\ \quad &f(−4)=(−4)^2+2(−4)−2 &f(2)=2^2+2·2−2 \\ \quad &f(−4)=16−8−2 &f(2)=4+4−2 \\ \quad &f(−4)=6\checkmark &f(2)=6\checkmark \end{array} & \end{array} \)
ⓑ Так як\(f(−4)=6\) і\(f(2)=6\), точки\((−4,6)\) і\((2,6)\) лежать на графіку функції.
Для функції\(f(x)=x^2−2x−8\),
ⓐ знайти,\(x\) коли\(f(x)=7\)
ⓑ Знайти дві точки, які лежать на графіку функції.
- Відповідь
-
ⓐ\(x=−3\) або\(x=5\)
ⓑ\((−3,7)\space (5,7)\)
Для функції\(f(x)=x^2−8x+3\),
ⓐ знайти,\(x\) коли\(f(x)=−4\)
ⓑ Знайти дві точки, які лежать на графіку функції.
- Відповідь
-
ⓐ\(x=1\) або\(x=7\)
ⓑ\((1,−4)\space (7,−4)\)
Властивість нульового продукту також допомагає нам визначити, де функція дорівнює нулю. Значення,\(x\) де знаходиться функція\(0\), називається нулем функції.
Для будь-якої функції\(f\), якщо\(f(x)=0\), то\(x\) дорівнює нулю функції.
Коли\(f(x)=0\), точка\((x,0)\) є точкою на графіку. Ця точка є\(x\) - перехоплення графіка. Часто важливо знати, де графік функції перетинає осі. Деякі приклади ми побачимо пізніше.
Для функції\(f(x)=3x^2+10x−8\) знайдіть
ⓐ нулі функції,
ⓑ any\(x\) -перехоплення графа функції
ⓒ any\(y\) -перехоплення графа функції
- Відповідь
-
ⓐ Щоб знайти нулі функції, нам потрібно знайти, коли значення функції дорівнює 0.
\(\begin{array} {ll} &f(x)=3x^2+10x−8 \\ \text{Substitute }0\text{ for}f(x). &0=3x^2+10x−8 \\ \text{Factor the trinomial.} &(x+4)(3x−2)=0 \\ \begin{array} {l} \text{Use the zero product property.} \\ \text{Solve.} \end{array} &\begin{array} {lll} x+4=0 &\text{or} &3x−2=0 \\ x=−4 &\text{or} &x=\frac{2}{3} \end{array} \end{array}\)
ⓑ\(x\) Перехоплення відбувається, коли\(y=0\). Так як\(f(−4)=0\) і\(f(\frac{2}{3})=0\), точки\((−4,0)\) і\((\frac{2}{3},0)\) лежать на графіку. Ці точки є\(x\) -перехопленнями функції.
ⓒ A\(y\) -перехоплення відбувається, коли\(x=0\). Щоб знайти\(y\) -перехоплення, нам потрібно знайти\(f(0)\).
\(\begin{array} {ll} &f(x)=3x^2+10x−8 \\ \text{Find }f(0)\text{ by substituting }0\text{ for }x. &f(0)=3·0^2+10·0−8 \\ \text{Simplify.} &f(0)=−8 \end{array} \)
Так як\(f(0)=−8\), точка\((0,−8)\) лежить на графіку. Ця точка є\(y\) -перехопленням функції.
Для функції\(f(x)=2x^2−7x+5\) знайдіть
ⓐ нулі функції
ⓑ any\(x\) -перехоплення графа функції
ⓒ any\(y\) -перехоплення графа функції.
- Відповідь
-
ⓐ\(x=1\) або\(x=\frac{5}{2}\)
ⓑ\((1,0),\space (\frac{5}{2},0)\) ⓒ\((0,5)\)
Для функції\(f(x)=6x^2+13x−15\) знайдіть
ⓐ нулі функції
ⓑ any\(x\) -перехоплення графа функції
ⓒ any\(y\) -перехоплення графа функції.
- Відповідь
-
ⓐ\(x=−3\) або\(x=\frac{5}{6}\)
ⓑ\((−3,0),\space (\frac{5}{6},0)\) ⓒ\((0,−15)\)
Розв'язуйте програми, змодельовані поліноміальними рівняннями
Стратегія вирішення проблем, яку ми використовували раніше для додатків, які переводять на лінійні рівняння, буде працювати так само добре для додатків, які переводяться на поліноміальні рівняння. Ми скопіюємо стратегію вирішення проблем тут, щоб ми могли використовувати її для довідки.
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
- Визначте, що ми шукаємо.
- Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
- Перевести в рівняння. Можливо, буде корисно повторити проблему в одному реченні з усією важливою інформацією. Потім перекладіть англійське речення в алгебраїчне рівняння.
- Розв'яжіть рівняння за допомогою відповідних методів алгебри.
- Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
- Відповісти на питання повним реченням.
Ми почнемо з числової задачі, щоб отримати практику перекладу слів у поліноміальне рівняння.
Добуток двох послідовних непарних цілих чисел дорівнює 323. Знайти цілі числа.
- Відповідь
-
\(\begin{array} {ll} \textbf{Step 1. Read }\text{the problem.} & \\ \textbf{Step 2. Identify }\text{what we are looking for.} &\text{We are looking for two consecutive integers.} \\ \textbf{Step 3. Name}\text{ what we are looking for.} &\text{Let } n=\text{ the first integer.} \\ &n+2= \text{ next consecutive odd integer} \\ \begin{array} {l} \textbf{Step 4. Translate }\text{into an equation. Restate the}\hspace{20mm} \\ \text{problem in a sentence.} \end{array} &\begin{array} {l} \text{The product of the two consecutive odd} \\ \text{integers is }323. \end{array} \\ &\quad n(n+2)=323 \\ \textbf{Step 5. Solve }\text{the equation.} n^2+2n=323 \\ \text{Bring all the terms to one side.} &n^2+2n−323=0 \\ \text{Factor the trinomial.} &(n−17)(n+19)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve the equations.} \end{array} &\begin{array} {ll} n−17=0 \hspace{10mm}&n+19=0 \\ n=17 &n=−19 \end{array} \end{array} \)
Є два значення для\(n\) того, щоб вирішити цю проблему. Таким чином, є два набори послідовних непарних цілих чисел, які будуть працювати.\(\begin{array} {ll} \text{If the first integer is } n=17 \hspace{60mm} &\text{If the first integer is } n=-19 \\ \text{then the next odd integer is} &\text{then the next odd integer is} \\ \hspace{53mm} n+2 &\hspace{53mm} n+2 \\ \hspace{51mm} 17+2 &\hspace{51mm} -19+2 \\ \hspace{55mm} 19 &\hspace{55mm} -17 \\ \hspace{51mm} 17,19 &\hspace{51mm} -17,-19 \\ \textbf{Step 6. Check }\text{the answer.} & \\ \text{The results are consecutive odd integers} & \\ \begin{array} {ll} 17,\space 19\text{ and }−19,\space −17. & \\ 17·19=323\checkmark &−19(−17)=323\checkmark \end{array} & \\ \text{Both pairs of consecutive integers are solutions.} & \\ \textbf{Step 7. Answer }\text{the question} &\text{The consecutive integers are }17, 19\text{ and }−19,−17. \end{array} \)
Добуток двох послідовних непарних цілих чисел дорівнює 255. Знайти цілі числа.
- Відповідь
-
\(−15,−17\)і\(15, 17\)
Добуток двох послідовних непарних цілих чисел дорівнює 483 Знайти цілі числа.
- Відповідь
-
\(−23,−21\)і\(21, 23\)
Ви були здивовані парою від'ємних цілих чисел, яка є одним з рішень попереднього прикладу? Добуток двох натуральних чисел і добуток двох від'ємних цілих чисел дають позитивні результати.
У деяких додатках негативні рішення будуть результатом алгебри, але не будуть реалістичними для ситуації.
Прямокутна спальня має площу 117 квадратних футів. Довжина спальні на чотири фути більше ширини. Знайдіть довжину і ширину спальні.
- Відповідь
-
Крок 1. Прочитайте проблему. У задачах, пов'язаних з
геометричними фігурами, начерк може допомогти вам візуалізувати
ситуацію.
Крок 2. Визначте, що ви шукаєте. Шукаємо довжину і ширину. Крок 3. Назвіть те, що ви шукаєте. Нехай\(w=\text{ the width of the bedroom}\). Довжина на чотири фути більше ширини. \(w+4=\text{ the length of the garden}\) Крок 4. Перевести в рівняння. Повторно викладіть важливу інформацію в реченні. Площа спальні 117 квадратних футів. Скористайтеся формулою для площі прямокутника. \(A=l·w\) Підставляємо в змінні. \(117=(w+4)w\) Крок 5. Вирішіть рівняння Розподіліть першим. \(117=w^2+4w\) Отримайте нуль з одного боку. \(117=w^2+4w\) Фактор триноміалу. \(0=w^2+4w−117\) Використовуйте властивість нульового продукту. \(0=(w^2+13)(w−9)\) Вирішіть кожне рівняння. \(0=w+13\quad 0=w−9\) Так як\(w\) це ширина спальні, не має
сенсу, щоб вона була негативною. Ми усуваємо це значення для\(w\).\(\cancel{w=−13}\)\(\quad w=9\) \(w=9\)Ширина - 9 футів. Знайти значення довжини. \(w+4\)
\(9+4\)
13 Довжина - 13 футів.Крок 6. Перевірте відповідь.
Чи має сенс відповідь?
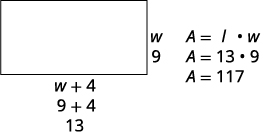
Так, в цьому є сенс.Крок 7. Дайте відповідь на питання. Ширина спальні становить 9 футів, а
довжина - 13 футів.
Прямокутний знак має площу 30 квадратних футів. Довжина знака на одну ногу більше ширини. Знайдіть довжину і ширину знака.
- Відповідь
-
Ширина - 5 футів, а довжина - 6 футів.
Прямокутний внутрішній дворик має площу 180 квадратних футів. Ширина внутрішнього дворика на три фути менше довжини. Знайдіть довжину і ширину патіо.
- Відповідь
-
Довжина внутрішнього дворика становить 12 футів, а ширина 15 футів.
У наступному прикладі ми будемо використовувати теорему Піфагора\((a^2+b^2=c^2)\). Ця формула дає відношення між катетами і гіпотенузою прямокутного трикутника.
Ми будемо використовувати цю формулу в наступному прикладі.
Вітрило човна має форму прямокутного трикутника, як показано на малюнку. Гіпотенуза буде довжиною 17 футів. Довжина однієї сторони буде на 7 футів менше довжини іншої сторони. Знайдіть довжини сторін вітрила.
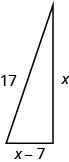
- Відповідь
-
Крок 1. Прочитайте проблему Крок 2. Визначте, що ви шукаєте. Шукаємо довжини
сторін вітрила.Крок 3. Назвіть те, що ви шукаєте.
Одна сторона на 7 менше, ніж інша.Нехай\(x=\text{ length of a side of the sail}\).
\(x−7=\text{ length of other side}\)Крок 4. Перевести в рівняння. Оскільки це
прямокутний трикутник, ми можемо використовувати теорему Піфагора.\(a^2+b^2=c^2\) Підставляємо в змінні. \(x^2+(x−7)^2=17^2\) Крок 5. Розв'яжіть рівняння
Спрощення.\(x^2+x^2−14x+49=289\) \(2x^2−14x+49=289\) Це квадратне рівняння, тому отримайте нуль з одного боку. \(2x^2−14x−240=0\) Фактор найбільший загальний фактор. \(2(x^2−7x−120)=0\) Фактор триноміалу. \(2(x−15)(x+8)=0\) Використовуйте властивість нульового продукту. \(2\neq 0\quad x−15=0\quad x+8=0\) Вирішити. \(2\neq 0\quad x=15\quad x=−8\) Так як\(x\) є стороною трикутника,\(x=−8\) не має
сенсу.\(2\neq 0\quad x=15\quad \cancel{x=−8}\) Знайдіть довжину іншої сторони. Якщо довжина однієї сторони дорівнює,
то довжина іншої сторони дорівнює


8 - довжина іншої сторони.Крок 6. Перевірте відповідь в проблемі
Чи мають сенс ці цифри?
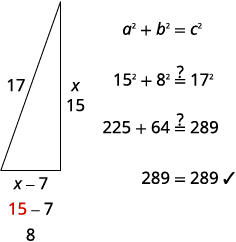
Крок 7. Відповісти на питання Сторони вітрила - 8, 15 і 17 футів.
Жюстін хоче поставити колоду в кутку свого заднього двору у формі прямокутного трикутника. Довжина однієї сторони палуби на 7 футів більше, ніж інша сторона. Гіпотенуза дорівнює 13. Знайдіть довжини двох сторін палуби.
- Відповідь
-
5 футів і 12 футів
Сад медитації має форму прямокутного трикутника, з однією ногою 7 футів. Довжина гіпотенузи на одну більше довжини іншого катета. Знайти довжини гіпотенузи і іншого катета.
- Відповідь
-
24 фути і 25 футів
У наступному прикладі використовується функція, яка дає висоту об'єкта як функцію часу, коли він кидається з 80 футів над землею.
Денніс збирається кинути свою гумку м'яч вгору з верхньої частини будівлі кампусу. Коли він кидає м'яч гумки з 80 футів над землею\(h\), функція\(h(t)=−16t^2+64t+80\) моделює висоту м'яча над землею як функція часу,\(t\). Знайти:
ⓐ нулі цієї функції, які повідомляють нам, коли м'яч потрапляє на землю
ⓑ коли м'яч буде 80 футів над землею
ⓒ висота м'яча в\(t=2\) секундах.
- Відповідь
-
ⓐ Нулі цієї функції знаходять шляхом розв'язання\(h(t)=0\). Це підкаже нам, коли м'яч вдарить об землю.
\(\begin{array} {ll} &h(t)=0 \\ \text{Substitute in the polynomial for }h(t). &−16t^2+64t+80=0 \\ \text{Factor the GCF, }−16. &−16(t^2−4t−5)=0 \\ \text{Factor the trinomial.} &−16(t−5)(t+1)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve.} \end{array} &\begin{array} {ll} t−5=0 &t+1=0 \\ t=5 &t=−1 \end{array} \end{array} \)Результат\(t=5\) говорить нам, що м'яч вдарить об землю через 5 секунд після того, як він буде кинутий. Оскільки час не може бути негативним, результат\(t=−1\) відкидається.
ⓑ М'яч буде на 80 футів над землею, коли\(h(t)=80\).
\(\begin{array} {ll} &h(t)=80 \\ \text{Substitute in the polynomial for }h(t). &−16t^2+64t+80=80 \\ \text{Subtract 80 from both sides.} &−16t^2+64t=0 \\ \text{Factor the GCF, }−16t. &−16t(t−4)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve.}\end{array} &\begin{array} {ll} −16t=0 &t−4=0 \\ t=0 &t=4 \end{array} \\ &\text{The ball will be at 80 feet the moment Dennis} \\ &\text{tosses the ball and then 4 seconds later, when} \\ &\text{the ball is falling.} \end{array} \)ⓒ Щоб знайти кульку висоти в\(t=2\) секундах, ми знаходимо\(h(2)\).
\(\begin{array} {ll} &h(t)=−16t^2+64t+80 \\ \text{To find }h(2)\text{ substitute }2\text{ for }t. &h(2)=−16(2)^2+64·2+80 \\ \text{Simplify.} &h(2)=144 \\ &\text{After 2 seconds, the ball will be at 144 feet.} \end{array}\)
Женев'єва збирається кинути скелю з вершини стежкою з видом на океан. Коли вона кидає скелю вгору з 160 футів над океаном\(h\), функція\(h(t)=−16t^2+48t+160\) моделює висоту скелі над океаном як функція часу,\(t\). Знайти:
ⓐ нулі цієї функції, які говорять нам, коли скеля потрапить в океан
ⓑ коли скеля буде на 160 футів над океаном.
ⓒ висота скелі в\(t=1.5\) секундах.
- Відповідь
-
ⓐ 5 ⓑ 0; 3 ⓒ 196
Каліб збирається кинути свою щасливу копійку зі свого балкона на круїзному лайнері. Коли він кидає копійку вгору з 128 футів над землею\(h\), функція\(h(t)=−16t^2+32t+128\) моделює висоту копійки над океаном як функція часу\(t\). Знайти:
ⓐ нулі цієї функції, коли пенні потрапить в океан
ⓑ коли пенні буде 128 футів над океаном.
ⓒ висота копійки буде в\(t=1\) секундах, тобто коли копійка буде в найвищій точці.
- Відповідь
-
ⓐ 4 ⓑ 0; 2 ⓒ 144
Отримайте доступ до цього інтернет-ресурсу для отримання додаткової інструкції та практики з квадратними рівняннями.
Ключові поняття
- Поліноміальне рівняння: Поліноміальне рівняння - це рівняння, яке містить поліноміальний вираз. Ступінь рівняння полінома - це ступінь многочлена.
- Квадратне рівняння: Рівняння\(ax^2+bx+c=0\) виду називається квадратним рівнянням.
\[a,b,c\text{ are real numbers and } a\neq 0\nonumber\]
- Нульова властивість продукту: Якщо\(a·b=0\), то\(a=0\) або\(b=0\) або або обидва.
- Як використовувати властивість нульового продукту
- Встановіть кожен коефіцієнт рівним нулю.
- Розв'яжіть лінійні рівняння.
- Перевірте.
- Як розв'язати квадратне рівняння шляхом факторингу.
- Запишіть квадратне рівняння в стандартному вигляді,\(ax^2+bx+c=0\).
- Фактор квадратичного виразу.
- Використовуйте властивість нульового продукту.
- Розв'яжіть лінійні рівняння.
- Перевірте. Підставляємо кожне рішення окремо в вихідне рівняння.
- Нуль функції: Для будь-якої функції\(f\), якщо\(f(x)=0\), то\(x\) дорівнює нулю функції.
- Як використовувати стратегію вирішення проблем для вирішення проблем зі словами.
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі.
- Визначте, що ми шукаємо.
- Назвіть те, що ми шукаємо. Виберіть змінну для представлення цієї кількості.
- Перевести в рівняння. Можливо, буде корисно повторити проблему в одному реченні з усією важливою інформацією. Потім перекладіть англійське речення в алгебраїчне рівняння.
- Розв'яжіть рівняння за допомогою відповідних методів алгебри.
- Перевірте відповідь в проблемі і переконайтеся, що це має сенс.
- Відповісти на питання повним реченням.
